二维Volterra积分方程Chebyshev谱配置解法及误差分析

2011-07-17陈少军王奇生

五邑大学学报（自然科学版） 2011年2期

关键词：定理数值方程

陈少军，王奇生

陈少军，王奇生

（五邑大学数学与计算科学学院，广东江门 529020）

利用乘积型Chebyshev多项式的Gauss、Gauss-Radau、Gauss-Lobatto点作为配置点，给出了二维Volterra积分方程的谱配置求解方法，同时给出了误差分析的结果.

二维Volterra积分方程；Chebyshev配置点；谱配置方法；误差分析

计算机的迅猛发展和快速Fourier变换的出现，大大减少了谱方法的计算量. 谱方法最受青睐的优越性在于它具有“无穷阶”的收敛速度，近年来，Volterra积分方程的谱配置解法引起了人们的广泛兴趣，如文献[1]给出了一类二维Volterra积分方程的数值试验，但没有给出计算方法的格式; 文献[2]给出了二维Volterra积分方程的Jacobi配置方程，但没有给出误差分析的结果; 文献[3]给出了二维Volterra积分方程的Legendre谱方法及误差估计的结果. 本文主要是研究二维Volterra积分方程的Chebyshev谱配置方法，并给出误差分析的结果.

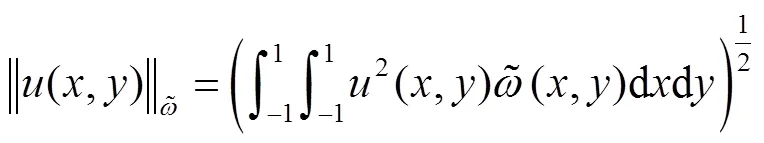
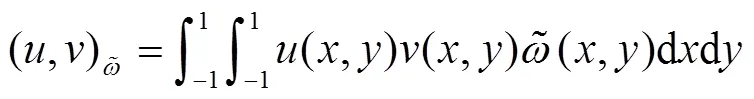
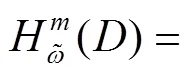
引入等价的半范数及离散内积的定义

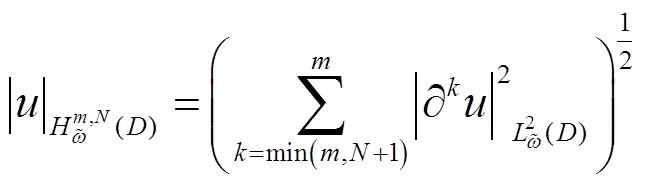
考虑下面的二维Volterra积分方程

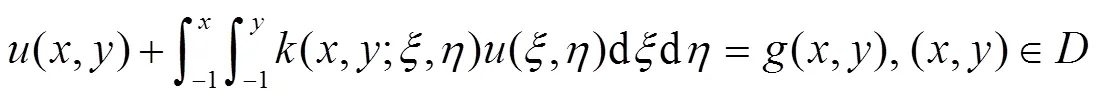
1 Chebyshev谱配置方法

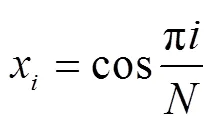
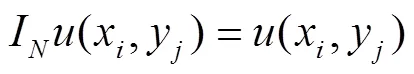
将配置点（2）代入方程（1）得到

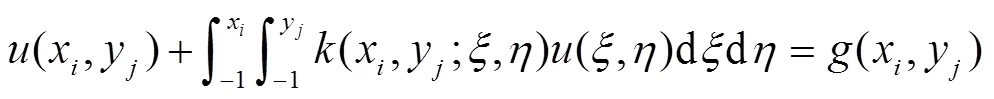
引入变换

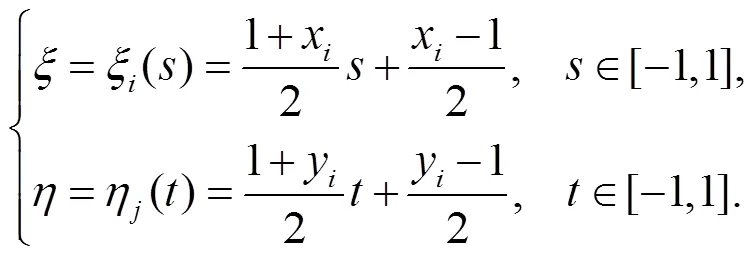
则方程（4）变换为

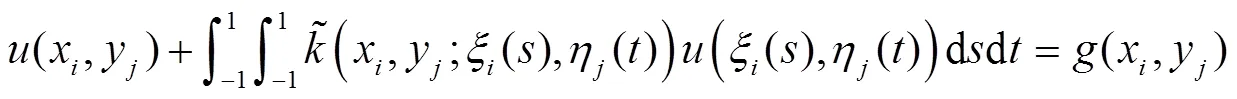
应用Gauss求积公式得:

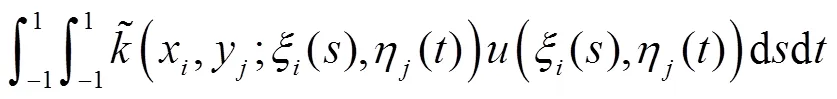
于是得到配置方程

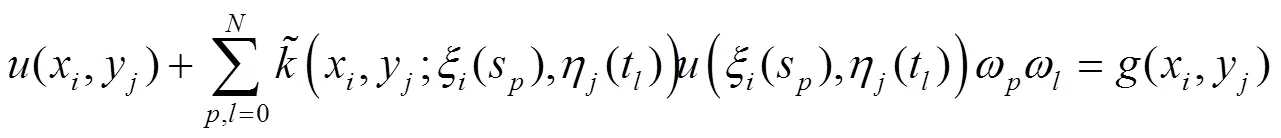
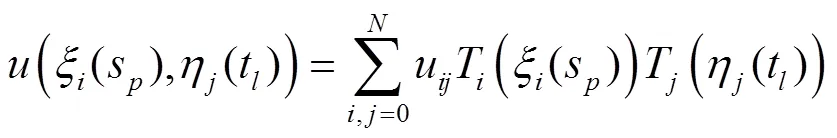
把式（7）代入式（6）得到

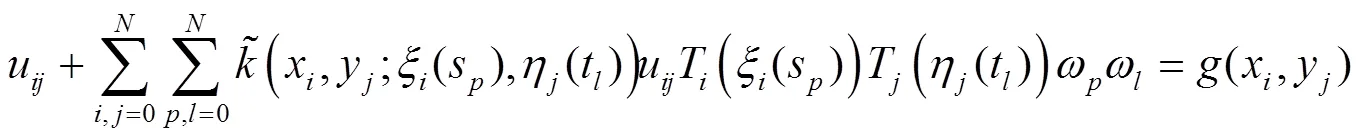
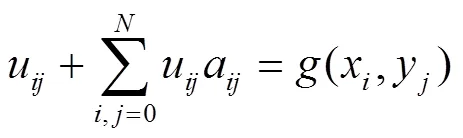
2 误差估计定理

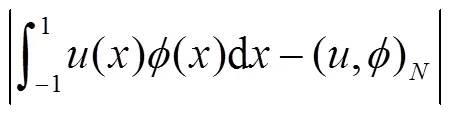
其中

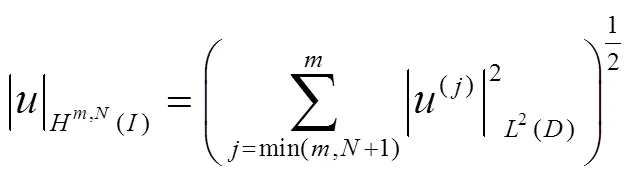
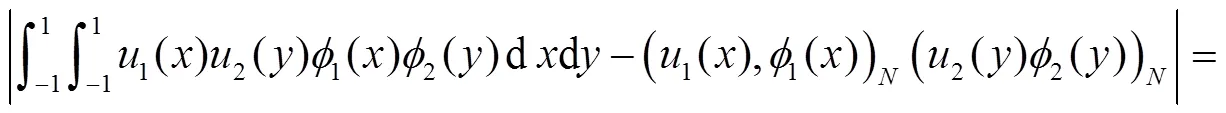
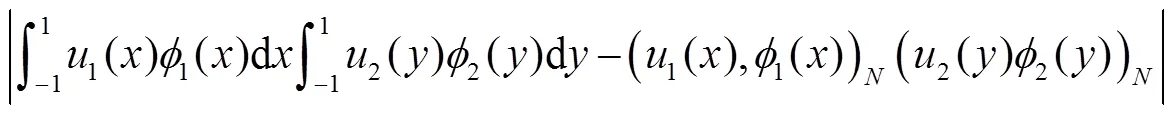
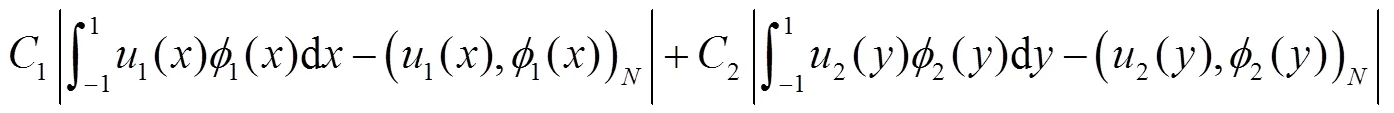
由引理1，得到

即定理成立.

下面给出二维Volterra积分方程Chebyshev谱配置解的误差分析结果.

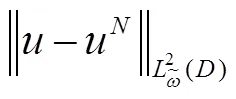
证明因为

整理得

由引理2得到

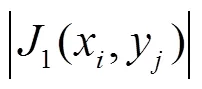
结合式（4）、（5）、（12），得

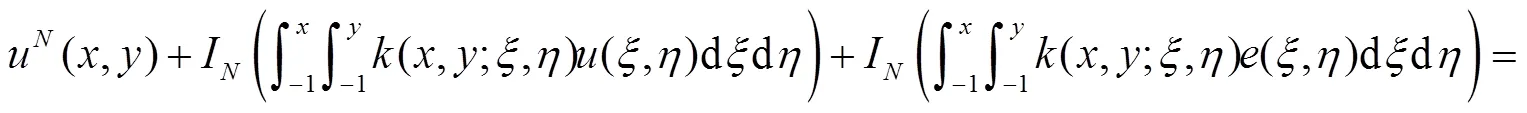
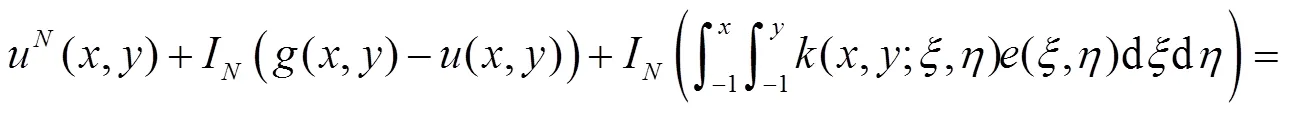
整理得

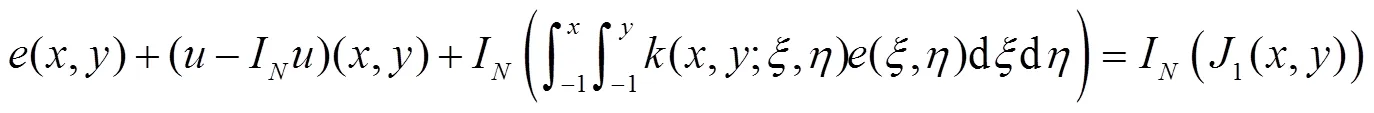
因此

其中

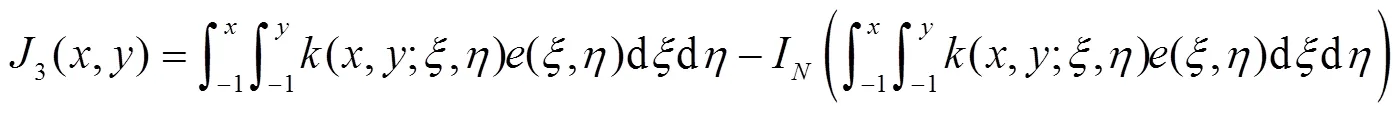
则

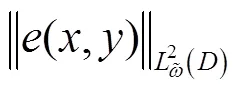
因为

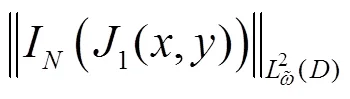
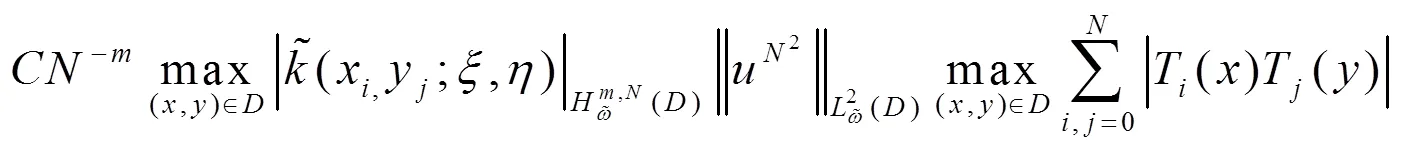
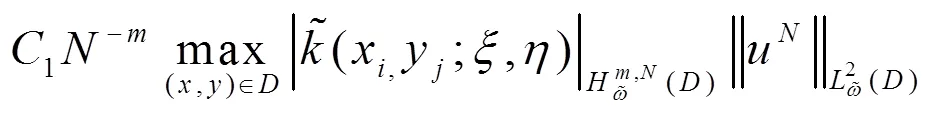
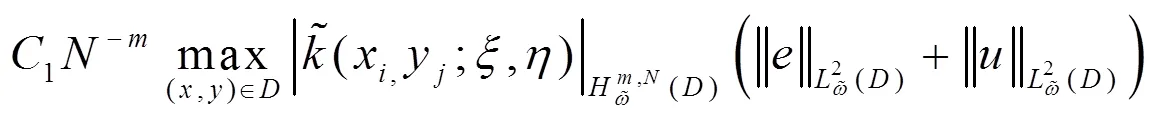
且

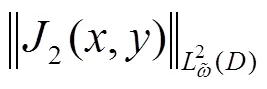
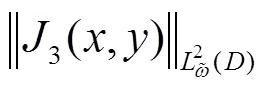
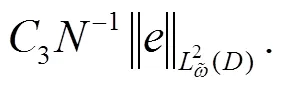
估计式（17）、（18）、（19），则

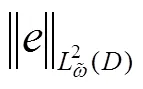
因此

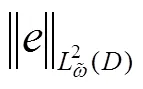
定理得证.

[1]CHEN Yanping, TANG Tao. Spectral methods for weakly singular volterra integral equations with smooth solutions[J]. Journal of Computational and Applied Mathematics, 2009, 233(4): 938-950.

[2]TANG Tao, XU Xiang, CHENG Jin. On spectral methods for volterra integral equations and the convergence analysis[J]. Journal of Computational Mathematics, 2008, 26(6): 825-837.

[3]CHEN Shaojun, WANG Qisheng. Legendre spectral method and convergence analysis for two dimension volterra integral equation[C]// Proceedings of the Ninth International Conference on Matrix Theory and its Applications. Shanghai: World Academic Press, 2010, 3: 121-124.

[4]CANUTO C, HUSSAINI M Y, QUARTERONI A, et al. Spectral methods: fundamentals in single domains. New York: Spring-Verlag, 2006.

Chebyshev Spectral Collocation Method and Error Analysis for the Two-dimensional Volterra Integral Equation

CHENShao-jun, WANGQi-sheng

(School of Mathematics and Computational Science, Wuyi University, Jiangmen 529020, China)

In this paper, the Chebyshev spectral collocation method for two-dimensional Volterra integral equation is obtained by using the Gauss, Gauss-Radau and Gauss-Lobatto points of product-type Chebyshev polynomials as collocation points. The results of the error analysis are also given.

the two-dimensional Volterra integral equation; Chebyshev collocation points; spectral collocation method; error analysis

1006-7302（2011）02-0015-05

O175. 5

2010-10-18

广东省自然科学基金资助项目（104529001005845）

陈少军（1982—）男，河南正阳人，硕士研究生，研究方向为微积分方程数值解法；王奇生，教授，博士，硕士生导师，通信作者，研究方向为微积分方程数值解法.