空间二仿射对应点列形成的双曲抛物面

刘阜平， 丁 勇

（太原理工大学，山西 太原 030024）

空间解析几何中，单叶双曲面和双曲抛物面属于二阶直纹曲面中的两种。在三维空间中，二射影点列对应点的连线包络成的二次曲面称为单叶双曲面；二仿射点列对应点的连线包络成的二次曲面称为双曲抛物面。利用二仿射对应点列在正投影图中的投影，可以容易地求出其导平面位置[1]，并且分析他们截交线的变化规律及其退化情况。

1 二仿射对应点列形成的双曲抛物面的直线型表示法

见图1，空间任意位置不相交的二仿射对应点列l1(I1，II1，Ⅲ1，…)，l2(I2，II2，Ⅲ2，…)都可以通过投影变换得到正投影图V/H。二仿射对应点列本身的度量性可以用仿射比来表示，当r＝1时为合同点列。l1l2二交叉直线夹角用 θ表示，可称为二线角。l1l2二交叉直线距离用a表示，可称为二线距。r，a和θ反映了空间二仿射对应点列的度量性。

二仿射对应点列具有两个共性。第一，二仿射对应点列正投影后仍为仿射对应点列，且对应关系不变。第二，在平面上二仿射点列对应点连线包络成抛物线[2]。

见图1，投影面V中能真实反映l1l2的仿射比r和二线角 θ的大小。为了求出导平面位置，只要让二点列在 H1面上投影后得到的新点列仿射比相等，并且同向即可。导平面是唯一的。为了叙述方便，令导平面方向用Pα表示；l1l2组成的平行平面方向用 Tα表示，Tα表示二点列对应非固有点连“线”。由于是非固有线，所以用平面表示方向。Tα与导平面 Pα夹角称为导面角。导面角用α表示。

图1 仿射点列确定的二次曲面直线型表示法

见图1，l1l2上所有对应点连线上总有一点属于点列l0(I0，II0，Ⅲ0，…)，l0和l1l2是一条同族直线[3]。l0l1，l0l2为底的点列也分别是仿射对应点列。l0平行于Tα。所有与l1l2同族的直线平行于 Tα。

因此得到二仿射对应点列形成的二次曲面的直线型表示法。见图2。

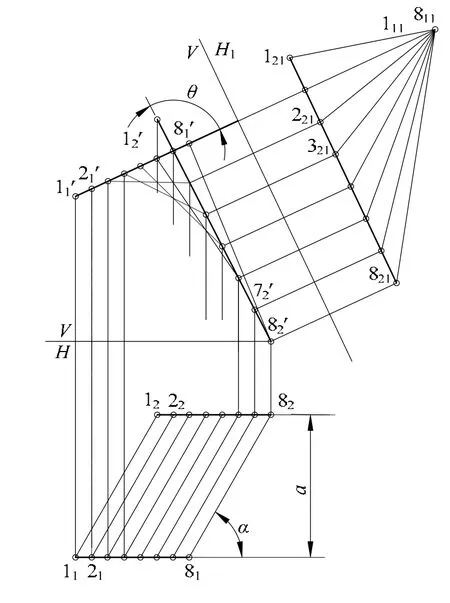
图2 双曲抛物面直线型表示法

第一，主平面V，V平行于Tα。在主平面V上，二点列l1l2反映实长，r和θ反映实际大小，二点列对应点连线包络成抛物线，就好像“压扁”了的双曲抛物面。简称为实形式投影图。

第二，副平面H，H垂直于Tα。在H面上，能真实反映二线距a和导面角α大小，简称为柱面式投影图。 对于每一个双曲抛物面，柱面式投影图是唯一的。

第三，次平面 H1，H2，H3，…，他们也垂直于Tα。在次平面上，必有一条同族直线lx投影积聚成点，简称为锥面式投影图。图1中H面投影也是锥面式投影图之一。

上述三种投影图，主平面和副平面是必须的，次平面可任意选择。为了让这种直线型曲面更有立体感，可以采用三线一般式表达方式，见图3。在图3中，V，H面与Tα既不平行也不垂直，三条同族直线不可能投影成点。

图3 双曲抛物面直线型表示法一般式

总之，在上述正投影图中，如果选取的视点不同，看到的双曲抛物面形状不同，实形式，柱面式，锥面式和一般式分别从不同角度反映了直线型双曲抛物面的形状。

2 双曲抛物面的截交线和退化

大家知道，二仿射对应点列l1(I1, II1, Ⅲ1,…),l2(I2, II2, Ⅲ2,…)，底l1l2互相交叉，称为同族直线。对应点，I1I2，II1II2，Ⅲ1Ⅲ2，…连线和l1，或者和l2是相交的，因此称为异族直线。属于I1I2交叉直线的平行平面Tα方向唯一。导平面Pα方向唯一。Tα和Pα交线方向S∞也唯一，如图4所示。

双曲抛物面截交线有下列几种情况：

（1）任意截平面如果通过同族直线或异族直线，截交线退化成直线。

（2）任意截平面如果平行于Tα，截交线退化成直线。见图4中正平面 K、S。当然，注意到这些直线的方向是不定的。他们也是与I0同样意义的同族直线，他们中任意一条都平行Tα，而且以这些直线为底的点列和 l1或 l2构成仿射对应，当然仿射比是分别不同的。可以用lx来表示这类直线。

（3）倾斜于Tα的截平面得到的截交线为抛物线。见图4中铅垂面R。抛物线轴线方向为Tα与导平面Pα交线S∞方向。

（4）垂直于 Tα的截平面得到的截交线为双曲线。见图5中的E、F平面。双曲线两条渐近线方向分别为截平面与 Tα平面交线和截平面与Pα平面交线表示的直线方向。

图4 双曲抛物面截交线为直线和抛物线

图5 双曲抛物面截交线为双曲线

上述结论（1）、（2）是明显的，（3）、（4）通过大量作图没有发现不同的结论。

3 二仿射对应点列形成双曲抛物面的度量性

见图1，二仿射对应点列 l1(I1, Ⅱ1, Ⅲ1, …)，l2( I2，II2，Ⅲ2，…) 形成双曲抛物面的底可以互换成同族直线中任意两条。如l0( I0，II0，Ⅲ0，…)和 l1(I1，Ⅱ1，Ⅲ1，…)形成的双曲抛物面和 I1I2形成的双曲抛物面是同一个。当然这时I0I1与I1I2仿射比、二线角、二线距都是不一样的。因此，仿射比、二线角、二线距只是两个对应点列之间度量性参数，并不能反映双曲抛物面的大小。衡量双曲抛物面的大小的主要参数是Tα、Pα以及它们的交线S∞方向、反映它们相互之间的位置参数导面角α。

如图6所示，当导面角为负α时，相对于图1，其它参数都不变，此时，可以认为形成了另一个大小相等，方向相反的双曲抛物面。

图6 反向双曲抛物面

如图7所示，如果I1I2为底的仿射点列是合同点列，即仿射比r =1，这时副平面H垂直于I1I2角分线。但是注意到其他同族直线，如 Ix与 I1为底的点列就不再是合同点列了。因此，两合同点列形成的双曲抛物面并不具备普遍性。

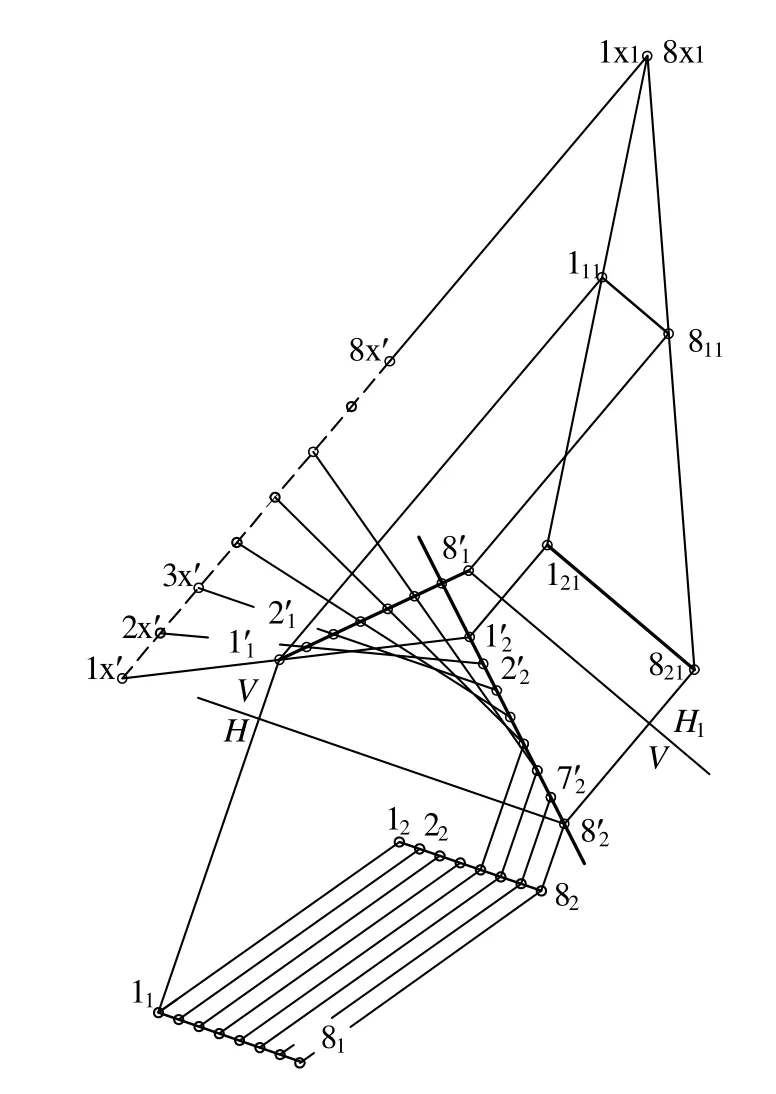
图7 二合同点列形成的双曲抛物面

当然，对于以I1I2为底的二仿射点列，如果只改变其中一个参数，如二线距a，或二线角θ，或仿射比r，都能得到一个新的双曲抛物面。

4 结束语

目前，虽然用解析几何讨论双曲抛物面已经比较全面，但是容易看出，用二仿射对应点列来分析，也有其特别之处。如对于截交线的退化，截交线为抛物线时轴线方向，截交线为双曲线时渐近线方向的表示就比较直观。而且利用二仿射对应点列构造一个双曲抛物面，用计算机来实现也相对变得简单。

[1]大连理工大学工程画教研室编. 画法几何学[M]. 北京: 高等教育出版社, 1992: 106.

[2]刘阜平, 丁 勇. 二射影对应点列与二级曲线[J].山西矿业学院学报, 1996, 52(4): 354-358.

[3]南开大学数学系《空间解析几何引论》编写组编. 空间解析几何引论[M]. 北京: 人民教育出版社, 1978:154-160.