两类形状可调五次广义Ball曲线
2011-07-31严兰兰温荣生
严兰兰, 张 文, 温荣生
两类形状可调五次广义Ball曲线
严兰兰, 张 文, 温荣生
(东华理工大学数学与信息科学学院,江西抚州344000)
定义了两种带形状参数的曲线。第一种曲线包含了五次Wang-Ball和Said-Ball曲线以及介于这两种曲线之间的无数曲线;第二种曲线包含了五次Said-Ball和Bézier曲线以及介于这两种曲线之间的无数曲线。通过分析这两种曲线与五次Bézier曲线之间的关系,得出了形状参数的几何意义,并给出了这两种曲线的几何作图法。
Wang-Ball基函数;Said-Ball基函数;Bernstein基函数;Ball曲线;形状参数
自数学家Ball在CONSURF机身曲面造型中提出一种三次参数曲线以来,广义Ball曲线面的研究工作大量展开,其中以Wang-Ball和Said-Ball曲线曲面为主。2000年邬弘毅提出了两类新的广义Ball曲线。2003年Delgado和Pena定义了DP-Ball基。在实践中人们发现Ball曲线面具有良好的保形性,且在求值及升降阶的计算速度上优于同次的Bézier曲线面。文献[8]通过增加的次数,得到了一组含参数的基函数,由之定义的曲线具有与三次Ball曲线类似的性质。文献[9-10]提出了带位置参数的广义Ball曲线,新曲线均包含Wang-Ball与Said-Ball曲线,以及介于二者之间的若干曲线。这里综合文献[8-10]的思想,通过构造两组分别含参数和的基函数,实现了从五次Wang-Ball基到Said-Ball基以及从五次Said-Ball基到Bernstein基的过渡,由这两组基定义的曲线均具有形状可调性。
1 介于Wang-Ball和Said-Ball曲线之间的曲线
1.1 基函数的构造与性质
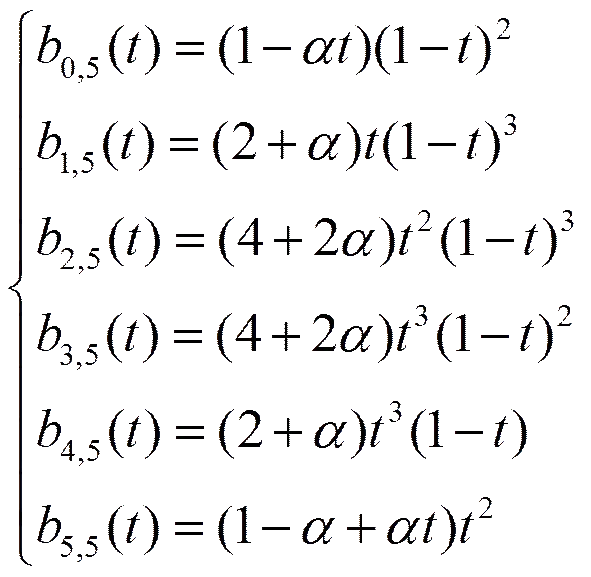
1.2 曲线的构造及性质
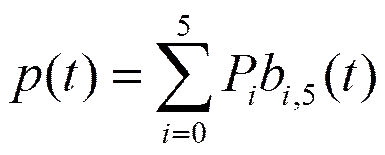
(4)几何不变性与仿射不变性。
1.3 形状参数的几何意义
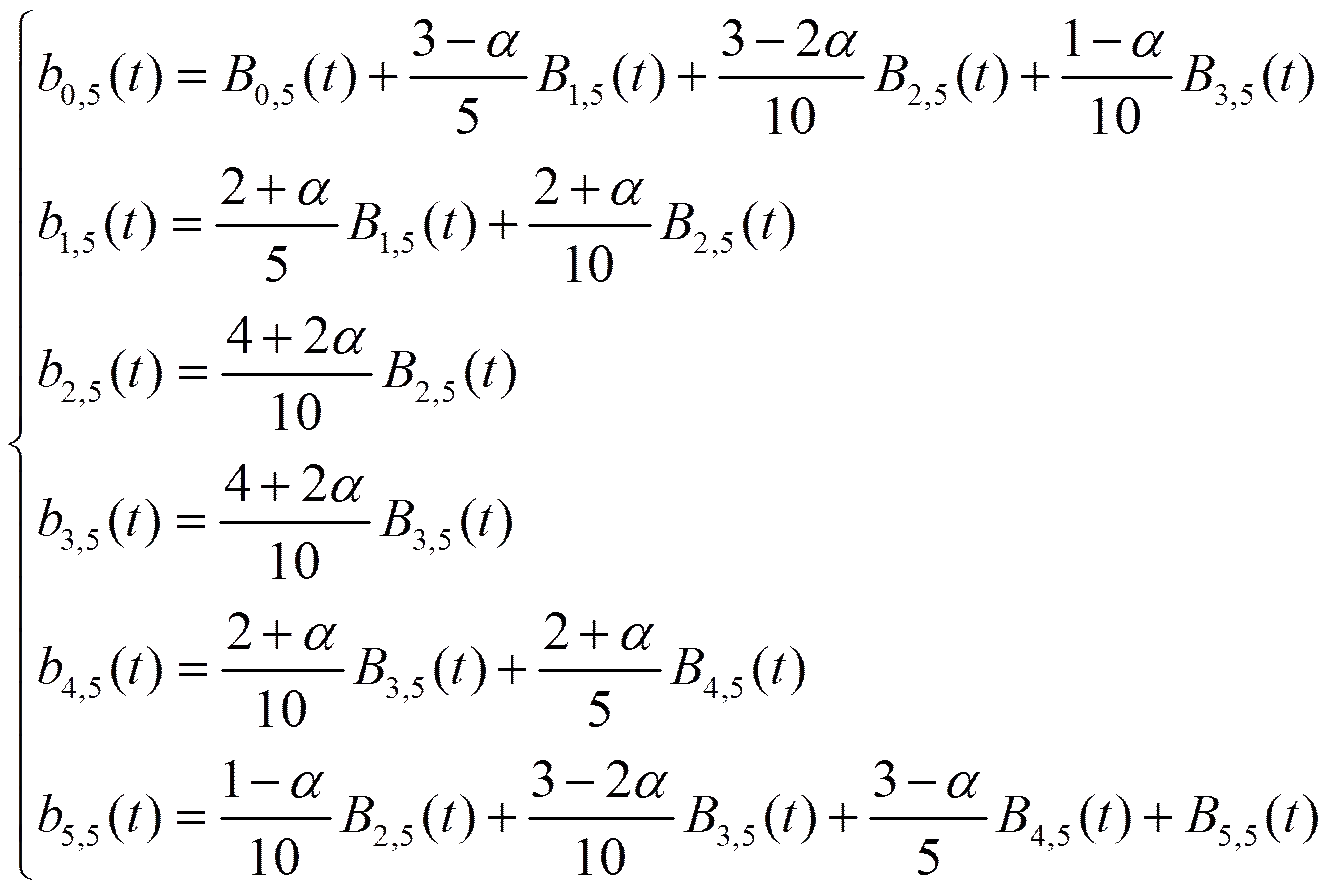
,,
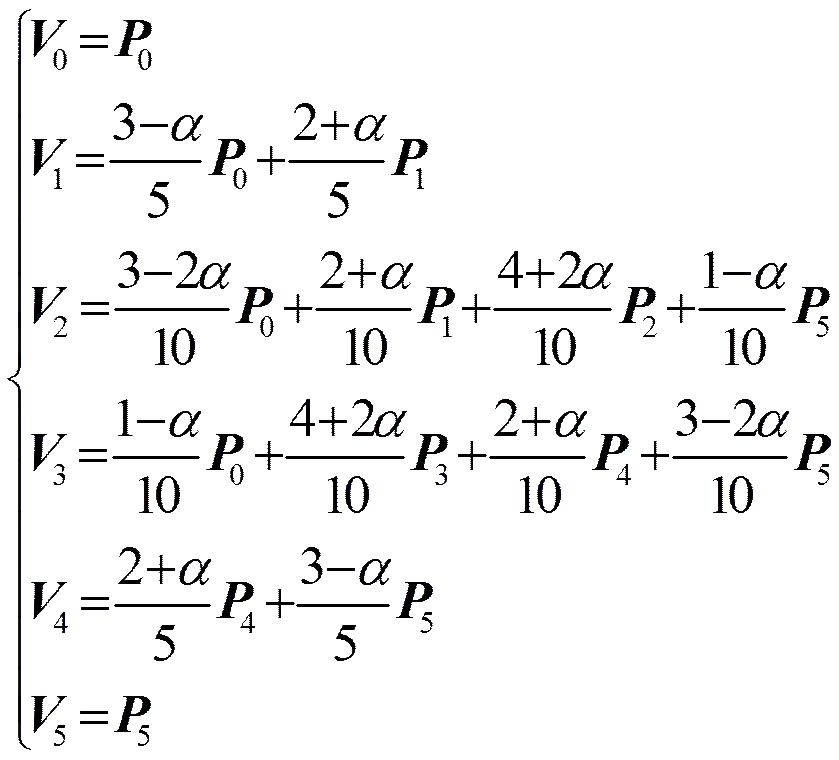

图1 B曲线中形状参数的几何意义
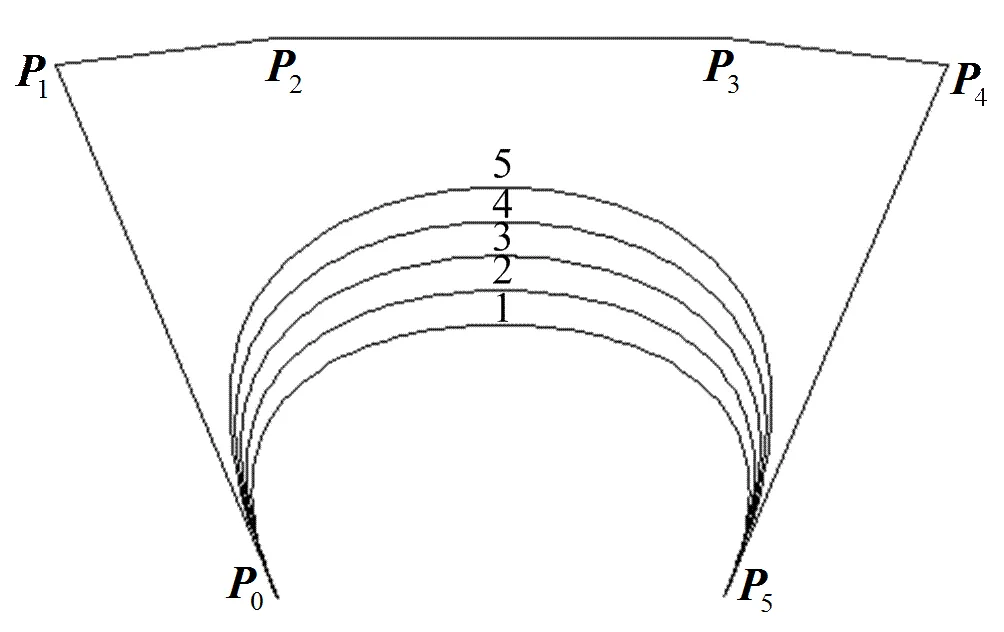
图2 取不同值时的B曲线
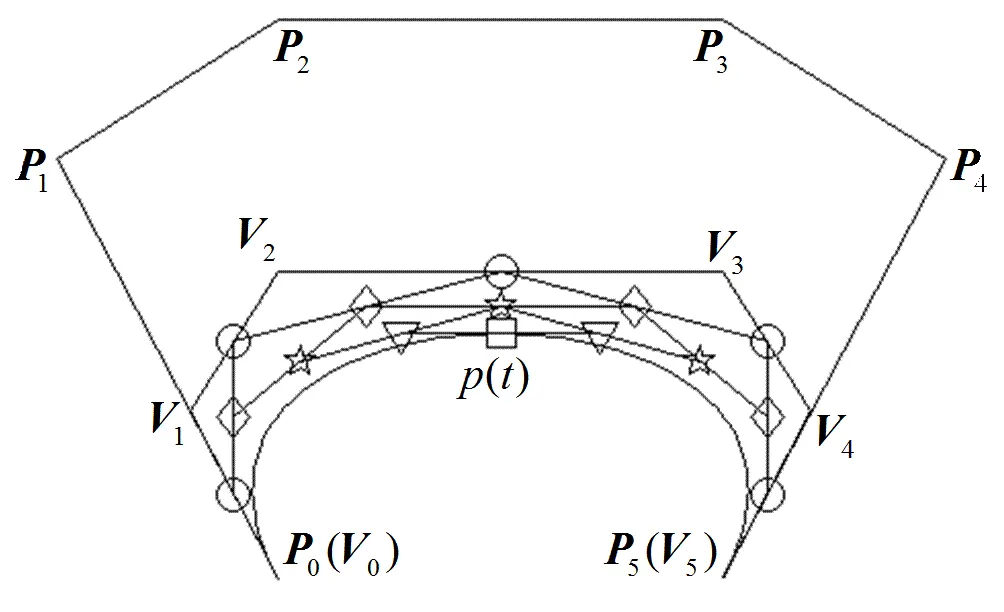
图3 B曲线的几何作图法
2 介于Said-Ball和Bézier曲线之间的曲线
2.1 基函数的构造与性质
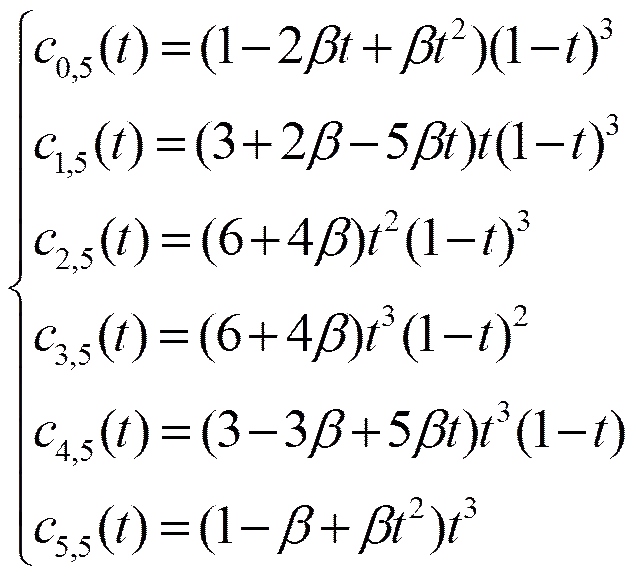
2.2 曲线的构造及性质
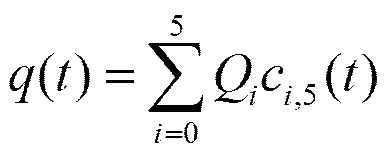
(2)凸包性。
(3)对称性。
(4)几何不变性与仿射不变性。
2.3 形状参数的几何意义
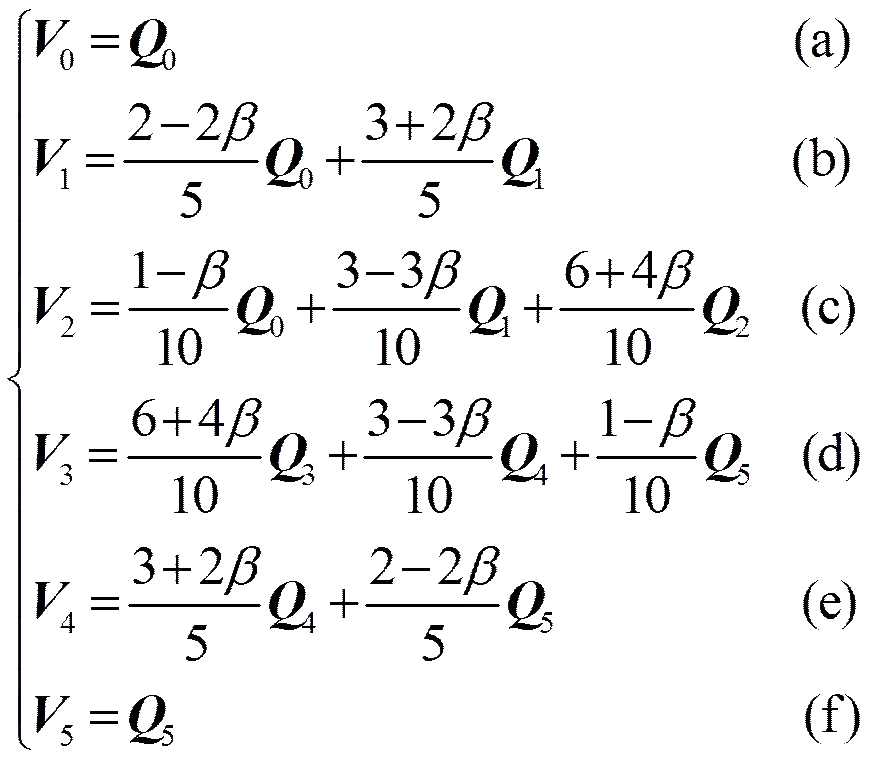
式(7)中(c)、(d)式可分别改写为
(8)
由形状参数的几何意义,并结合Bézier曲线的逼近性可知,越大,B曲线越靠近其控制多边形,如图5所示。图中曲线1~5依次取,曲线1和5分别为五次Said-Ball和Bézier曲线。
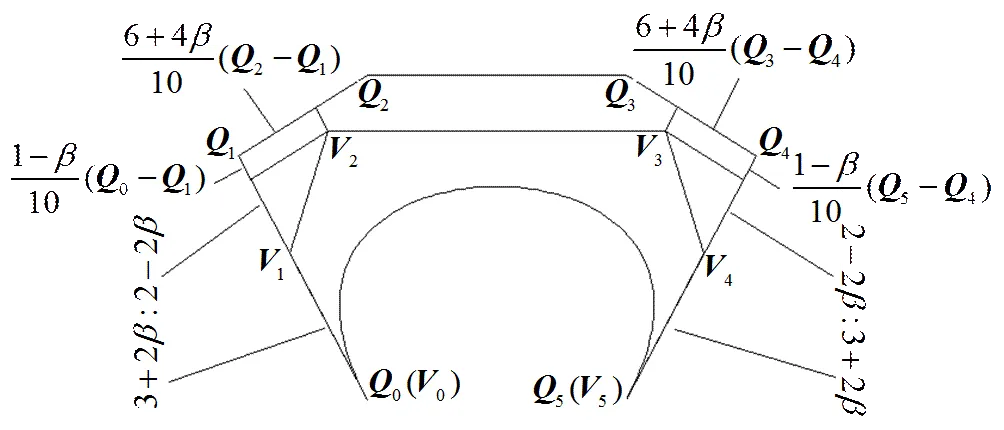
图4 B曲线中形状参数的几何意义
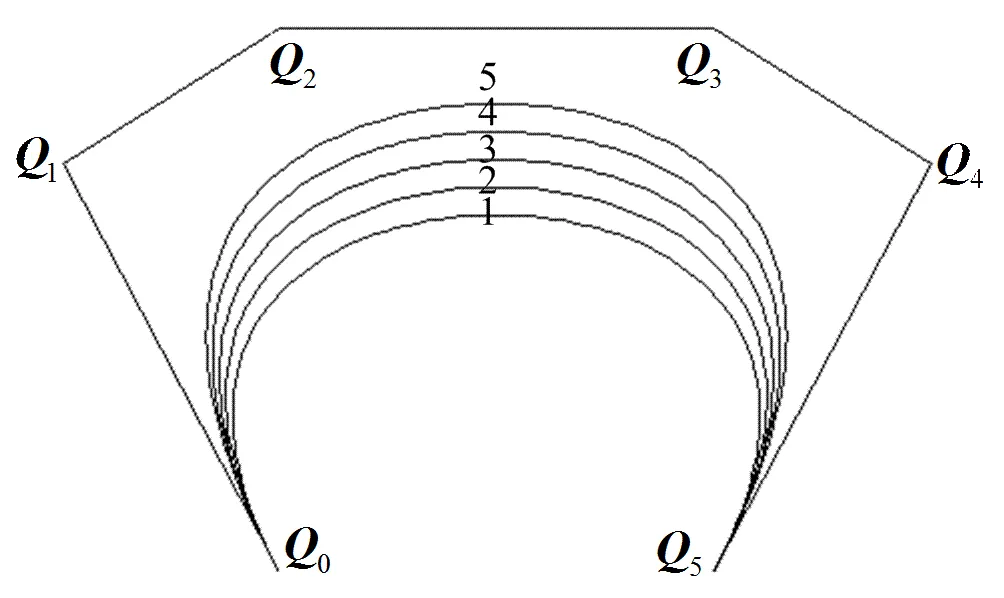
图5 取不同值时的B曲线
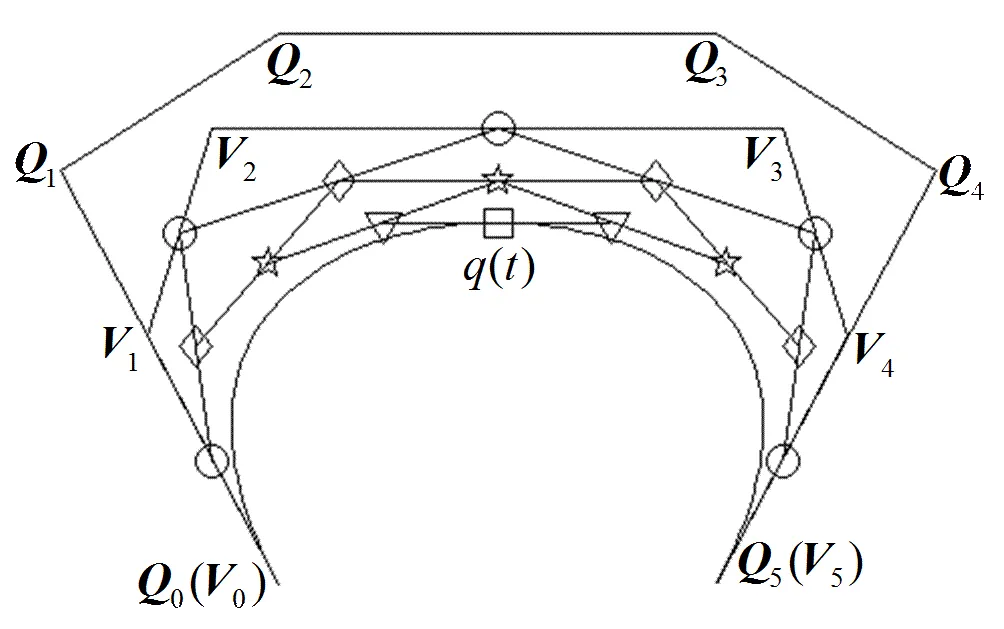
图6 B曲线的几何作图法
3 结束语
这里给出的两种曲线生成方法,不仅分别以五次Wang-Ball和Said-Ball曲线以及五次Said-Ball和Bézier曲线为特例,而且由于带有形状参数,所以可以在不改变控制多边形的情况下对曲线的形状和位置进行调整,从而分别得到介于五次Wang-Ball和Said-Ball曲线之间以及介于五次Said-Ball和Bézier曲线之间的无数中间曲线。与文献[9]和文献[10]中的方法相比,这里给出的是基函数的显式表示,而且基函数的表达式相对比较简单。另外,这里得到中间曲线的方法也很简单,只要改变形状参数的值即可,而且中间曲线的条数是无限的,与曲线的次数无关。并且这里的形状参数均具有明确的几何意义,所以可以很方便地选择其值来得到所需要的中间曲线。
[1] Ball A A. CONSURF, Part 1: Introduction to the conic lofting title [J]. Computer Aided Design, 1974, 6(4): 243-249.
[2] Ball A A. CONSURF, Part 2: Description of the algorithms [J]. Computer Aided Design, 1975, 7(4): 237-242.
[3] Ball A A. CONSURF, Part 3: How the program is used [J]. Computer Aided Design, 1977, 9(1): 9-12.
[4] 王国瑾. 高次Ball曲线及其几何性质[J]. 高校应用数学学报, 1987, 2(1): 126-140.
[5] Said H B. Generalized Ball curve and its recursive algorithm [J]. ACM Trans. on Graphics, 1989, 8(4): 360-371.
[6] 邬弘毅. 两类新的广义Ball曲线[J]. 应用数学学报, 2000, 23(2): 196-205.
[7] Delgado J, Pena J M. A shape preserving representation with an evaluation algorithm of linear complexity [J]. Computer Aided Geometric Design, 2003, 20(1): 1-10.
[8] 王成伟. 三次Ball曲线的扩展[J]. 工程图学学报, 2008, 29(1): 77-81.
[9] Wu H Y. Unifying representation of Bézier curve and generalized Ball curves [J]. Applied Mathematics: A Journal of Chinese Universities, 2000, 15(1): 109-121.
[10] 沈莞蔷, 汪国昭. Ball基的推广[J]. 软件学报, 2005, 16(11): 1992-1999.
Two Classes of Quintic Generalized Ball Curves with Adustable Shape
YAN Lan-lan, ZHANG Wen, WEN Rong-sheng
( College of Mathematics and Information Science, East China Institute of Technology, Fuzhou Jiangxi 344000, China )
Two new classes of curves with shape parameters are defined. The first class of curve contains the quintic Wang-Ball and Said-Ball curves and the curves located between them. The second class of curve contains the quintic Said-Ball and Bézier curves and the curves located between them. By analyzing the relationship between the new curves and the quintic Bézier curve, the geometric meaning of shape parameters are obtained, and the geometrical drawing method of the new curves are given.
Wang-Ball basis function; Said-Ball basis function; Bernstein basis function; Ball curve; shape parameter
TP 391
A
1003-0158(2011)06-0016-05
2008-07-16
严兰兰(1982-),女,湖北浠水人,讲师,硕士,主要研究方向为计算机辅助几何设计。
