一类带两个形状参数的类四次三角Bézier曲线

杨 炼，李军成



一类带两个形状参数的类四次三角Bézier曲线

杨 炼，李军成

（湖南人文科技学院数学系，湖南娄底417000）

给出了带两个形状参数，的类四次三角多项式Bézier曲线。该曲线不仅具有与四次Bézier曲线类似的性质，而且无需有理形式即可精确表示圆、椭圆、抛物线等二次曲线弧以及高精度近似表示圆柱螺线等超越曲线。利用两个参数的不同取值能够局部或整体调控曲线的形状，并且可以从两侧逼近控制多边形。讨论了两段曲线和连续的拼接条件。实例表明，该曲线在造型设计方面具有较高的应用价值。

Bézier曲线；三角多项式；类四次；形状参数；拼接性

在计算机辅助几何设计中，低次Bézier曲线与B样条曲线因其结构简单、使用方便等特点而成为构造自由曲线、曲面的常用工具，然而它们却不能精确表示圆弧等二次曲线。有理Bézier曲线和NURBS曲线虽然解决了上述问题，但是其求导和求积的计算较复杂，且权因子选择和参数化问题至今还没有完全解决。近年来，人们对非多项式曲线，特别是三角多项式曲线样条的研究产生了兴趣，开始在带三角函数的空间上寻求构造曲线曲面的表示方法，其中文献[5]基于{1,, sin, cos}构造了著名的-曲线，文献[6]与文献[7]分别构造了带形状参数的二次与三次三角多项式曲线；文献[8]提出了一组具有Bézier曲线特征的T-Bézier曲线；文献[9-10]研究了形状可调的二次三角Bézier曲线；文献[11-12]以三角函数为基构造了类三次参数曲线。

本文研究一种带有两个形状参数,的具有四次Bézier曲线特性的三角多项式曲线，称之为带两个参数的类四次三角Bézier曲线。事实表明，这种带两个参数的类四次三角Bézier曲线不仅与相应的四次Bézier曲线具有绝大部分相似的性质，而且在适当条件下还可精确表示直线段、椭圆（圆）弧、抛物线、心脏线等二次曲线以及高精度近似表示圆柱螺线等超越曲线。

形状参数λ, λ具有明确几何意义：当增大时，曲线从左侧逼近控制多边形，当增大时曲线从右侧逼近控制多边形；当=时，曲线就成为带一个形状参数的类四次三角Bézier曲线；当,同时增大时，曲线整体逼近控制多边形。

1 基函数的定义

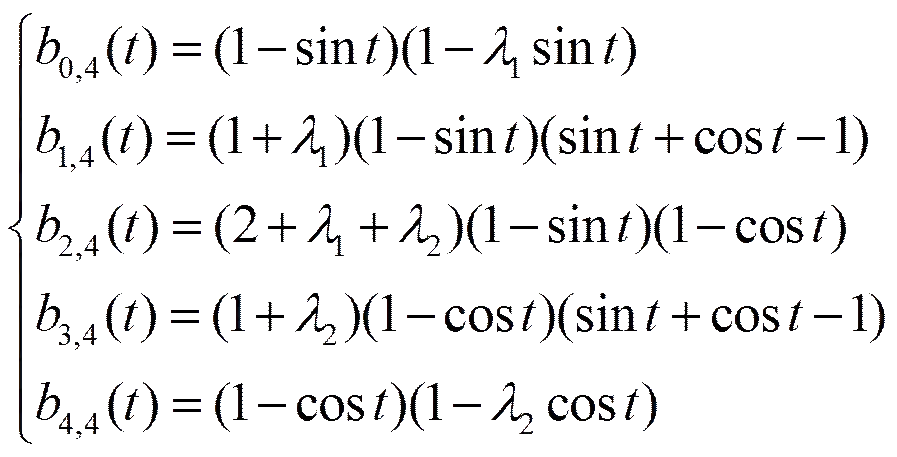
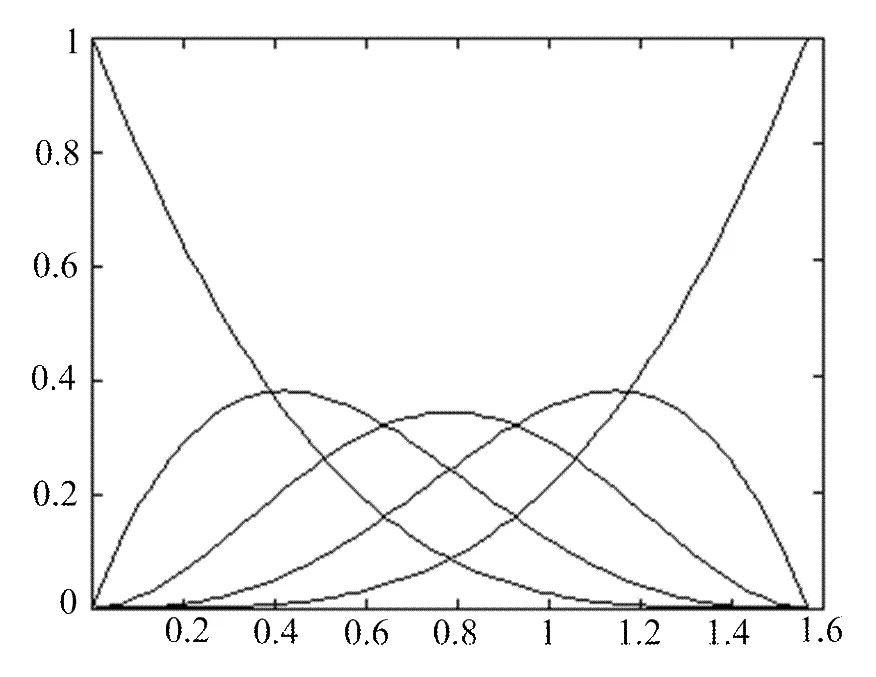
图1 5个基函数图形(λ1=λ2= 1)

2 类四次三角Bézier曲线及性质

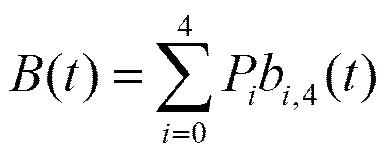
称式(2)所定义的曲线为带两个形状参数的类四次三角Bézier曲线。

由基函数性质，可以导出曲线具有下列几何性质：

性质1 端点性质

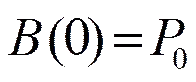
（3）

式(3)说明曲线具有与四次Bézier曲线完全相同的端点性质：插值于首末两个端点且与端边相切。

性质2 对称性

性质3 凸包性与保凸性

由基函数的非负性和权性，可知曲线是落在其控制顶点生成的凸包之内。另外，当控制多边形为凸时，相应的曲线也是凸的，即曲线具有保凸性。

性质4 几何不变性和仿射不变性

曲线仅依赖于控制顶点而与坐标系的位置和方向无关，即曲线的形状在坐标平移和旋转后不变；同时，对控制多边形进行缩放或剪切等仿射变换后，所对应的新曲线就是相同仿射变换后的曲线。

3 形状参数对曲线的调节作用

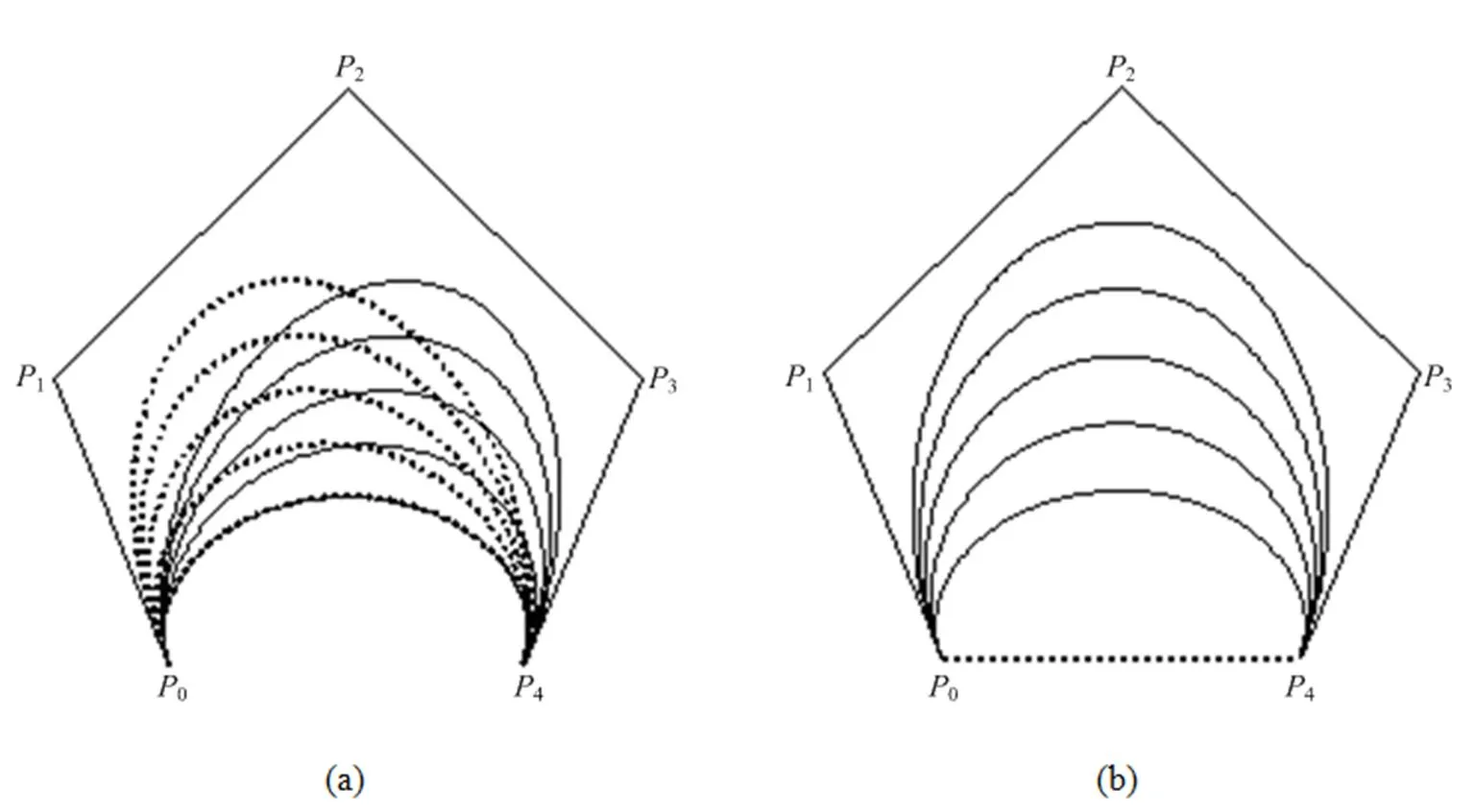
图2 形状参数对类四次三角Bézier曲线的影响

4 曲线的拼接

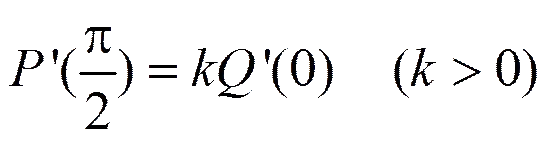
将式(3)代入上式得

,

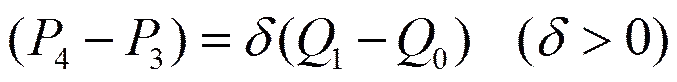
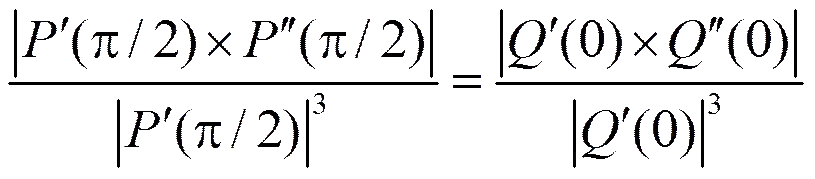
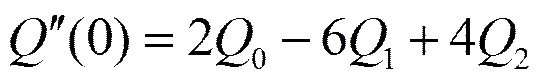
将式(3)和式(6)代入式(5)，化简可得

将式(4)代入上式，可得

图3 两段曲线的G2拼接(δ=1.5, h2=2.25h1)

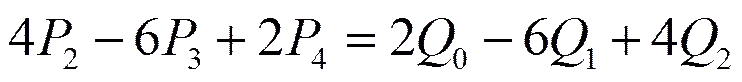
综合以上三式，可解得

（8）

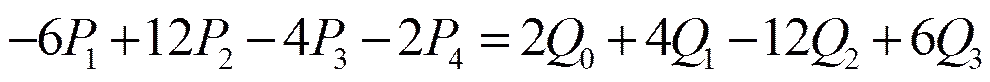
综合前面的条件，可解得

（9）

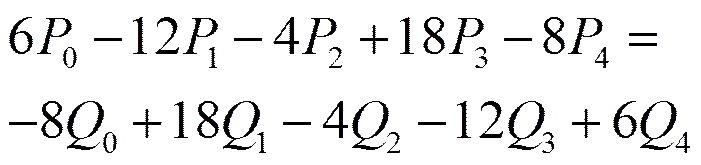
综合前面的条件，可解得

（10）

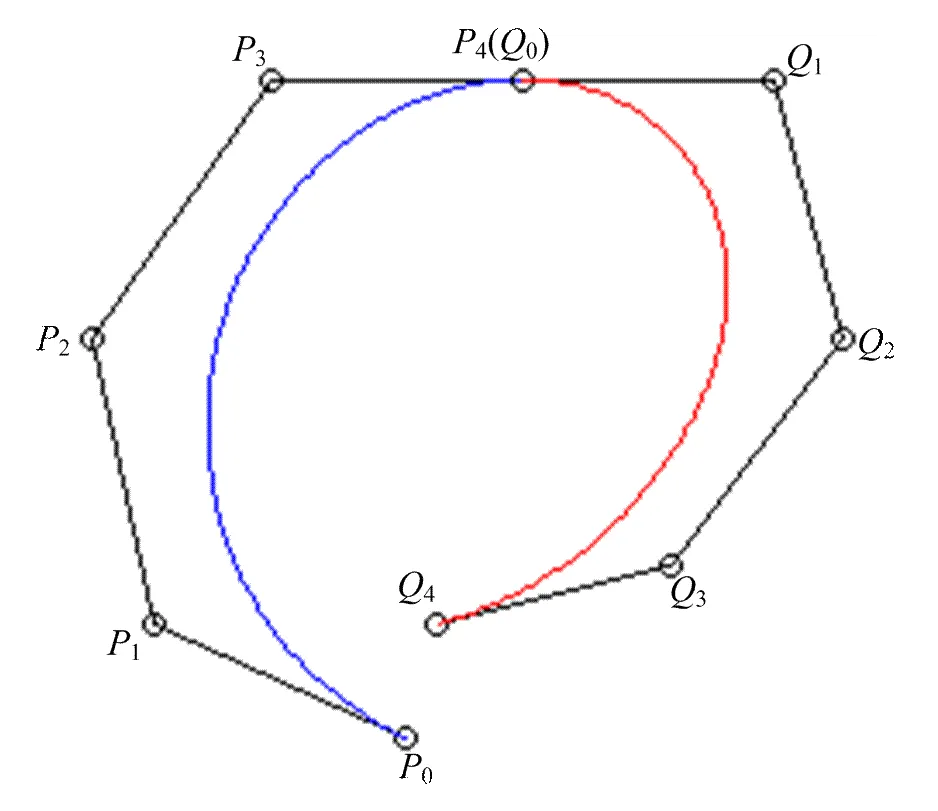
图4 两段曲线的C4拼接

5 曲线的应用实例

5.1 椭圆弧与圆弧的精确表示

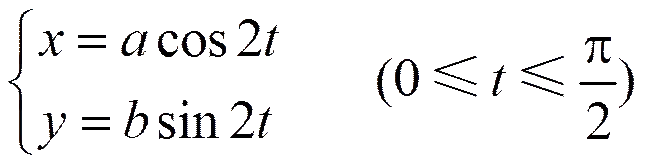
当（或）时，上式表示半椭圆（圆）弧；时表示上半椭圆（圆），时表示下半椭圆（圆）。当,时椭圆（圆）弧的精确表示如图5、图6所示。

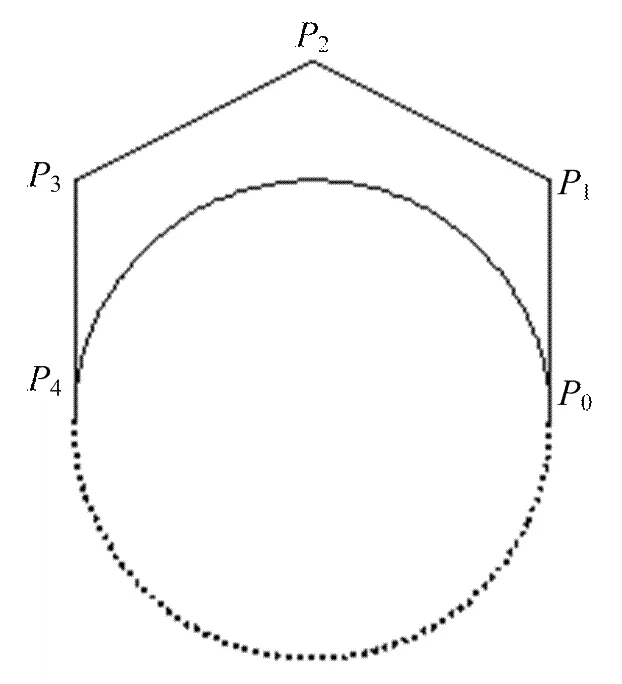
图6 圆弧的精确表示

5.2 心脏线的精确表示

即，。显然，当满足上述条件时，曲线式(2)精确表示一段心脏线（如图7所示）。

5.3 抛物线的精确表示

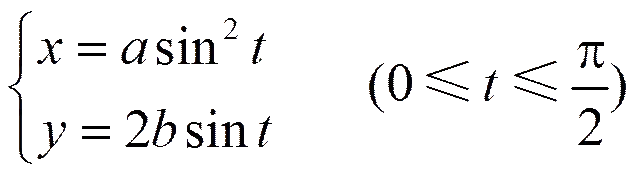
上式显然表示一段抛物线弧，其图形如图8所示。

5.4 圆柱螺线的高精度近似表示

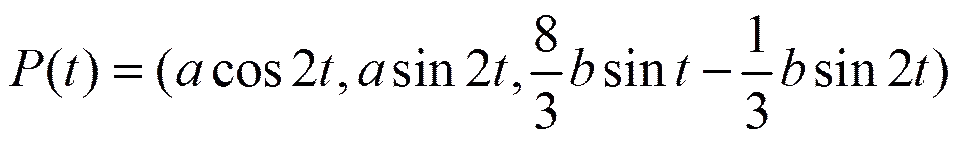
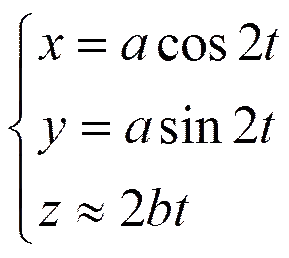
上式便是近似圆柱螺线方程，得证。

5.5 花瓣图形

开曲线和闭曲线的构造是曲线设计中最基本的内容，在工业设计中需要研究开曲线的端点性质和如何构造闭曲线。带两个形状参数的类四次三角Bézier曲线具有较强的造型功能，它可以表示开曲线和闭曲线的模型。图10(a)、图10(e)是当两个参数相等且同时由大到小变化时开曲线的花瓣图形；图10(b)、图10(c) 是当两个参数相等且同时由大到小变化时闭曲线的花瓣图形；图10(d)、图10(f)分别是当两个参数一个增大，另一个减少时开、闭曲线的花瓣图形。

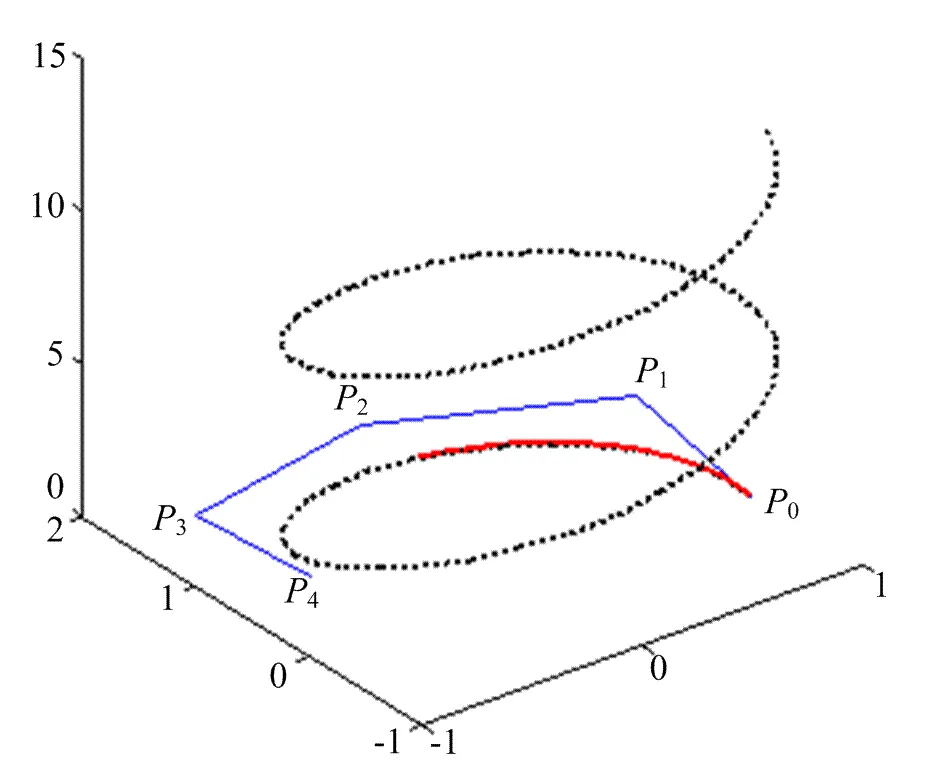
图9 圆柱螺线的高精度近似表示

图10 花瓣图形的拟合

6 结束语

提出的一种由三角多项式基函数构造的带有参数λ, λ的类四次三角Bézier曲线，它与四次Bézier曲线具有类似的特征。该曲线的优点是：① 对于给定的5个控制顶点，可以生成一簇三角Bézier曲线，这簇曲线在参数的控制下，能够局部或整体调节曲线的形状，方便造型设计；② 曲线在一定条件下，可以精确表示直线段、椭圆（圆）、抛物线等二次曲线以及高精度近似表示圆柱螺线等超越曲线；③ 曲线在一定条件下可进行和的连续拼接，具有良好的拼接性。运用张量积的方法，可将曲线推广到曲面情形，曲面具有与曲线类似的性质。

[1] 施法中. 计算机辅助几何设计与非均匀有理B样条[M]. 北京: 高等教育出版社, 2001: 306-454.

[2] 王国瑾, 汪国昭, 郑建民. 计算机辅助几何设计[M].北京: 高等教育出版社, 2001: 1-33.

[3] Mainar E, Pea T M, Sanchez-Reyes J. Shape preserving alternatives to the rational Bézier model [J]. Computer Aided Geometric Design, 2001, 18: 37-96.

[4] Pieg L, Tiller W. The NURBS book (2nd ed) [M]. Berlin Heidelberg: Springer, 1997: 289-311.

[5] Zhang Jiwen. C-curves: an extension of cubic curves [J]. Computer Aided Geometric Design, 1996, 13(3): 199-217.

[6] Han Xuli. Quadratic trigonometric polynomial curves with a shape parameter [J]. Computer Aided Geometric Design, 2002, 19(7): 503-512.

[7] Han Xuli. Cubic trigonometric polynomial curves with a shape parameter [J]. Computer Aided Geometric Design, 2004, 21(6): 535-548.

[8] 苏本跃, 黄有度. 一类Bézier型的三角多项式曲线[J]. 高等学校计算数学学报, 2005, 27(3): 202-208.

[9] 吴晓勤, 韩旭里, 罗善明. 带形状参数的二次三角Bézier三角曲线[J]. 工程图学学报, 2008, 29(1): 82-87.

[10] 唐运梅, 吴晓勤, 韩旭里. 基于三点形状可调的二次三角Bézier曲线[J]. 计算机工程与科学, 2010, 32(3): 66-68.

[11] 李军成, 宋来忠. 一组基于三角函数的类三次参数曲线[J]. 计算机工程与设计, 2009, 29(10): 2702-2704.

[12] 李军成, 陈国华, 杨笃庆. 可调的类三次Bézier三角曲线[J]. 计算机工程与科学, 2010, 32(3): 69-71.

A Class of Quasi-quartic Trigonometric Polynomial Bézier Curves with Two Shape Parameters

YANG Lian, LI Jun-cheng

( Department of Mathematics, Hunan Institute of Humanities, Science and Technology, Loudi Hunan 417000, China )

A class of quasi-quartic trigonometric polynomial Bézier curves with two shape parameters ofandis presented. The trigonometric polynomial curves have the same featurs with traditional quartic Bézier curves, and it can represent exactly some quadratic curves such as the arc of a circle, an ellipse, or a parabola and some transcendental curves such as circular helixwithout using rational form. Its shape can be adjusted locally or totally through changing the value of the two parameters, and it can approach to the given control polygon from both sides. Theandcontinuity condition of two pieces of curves is discussed. Examples are given to illustrate the new curve in model design.

Bézier curves; trigonometric polynomial; quasi-quartic; shape parameter; continuity

TP 391

A

1003-0158(2011)06-0009-07

2010-07-21

湖南人文科技学院科研资助项目（2010QN09）；湖南省教育厅科研资助项目（11C0707）

杨 炼（1980-），男，湖南隆回人，讲师，硕士，主要研究方向为计算机图形学，计算机辅助几何设计。