基于场路耦合的方向可控电磁发射器发射过程研究

王慧锦，王成学，曹延杰，陈学慧

（海军航空工程学院，山东 烟台 264001）

机动性和防护性是影响坦克和装甲车辆战场生存能力的重要特性［1］。为了提高坦克和装甲车辆的战场生存能力，各国致力于研究和发展多种新型装甲，其中电磁装甲就是一种很有发展前景的新型装甲［2］。电磁装甲可分为主动电磁装甲和被动电磁装甲，按照原理的不同，主动电磁装甲又分为线圈感应式和磁场重接式两种［3］。

线圈感应式主动电磁装甲主要由探测系统、控制系统、高功率脉冲电源、开关和发射装置组成，其中发射装置是线圈感应式主动电磁装甲的一个关键部件。方向可控电磁发射器是一种双线圈发射装置，主要由拦截弹、发射线圈、绝缘材料和底座组成。

在电磁发射器的发射过程中，拦截弹的运动特性对电容器组的放电过程影响很大，文献［4－5］结合有限元法和实验分析了电磁发射器的发射过程，分析时施加到发射线圈上的电流是通过实验测得并作为已知量给出，电流载荷是固定的，而在实际中，发射线圈的激励为电压源（脉冲电容器组），电流是未知的。电磁发射器发射过程涉及电磁、机械和运动的耦合问题，发射线圈、拦截弹和电容器组中的任一参数发生变化时，放电电流都会发生变化。文献中的方法不能很好地进一步指导电磁发射器的实验研究，为了系统地分析发射器的工作过程，必须考虑外部电压源对拦截弹动态特性的影响［6－8］。

场路耦合法是在场计算基础上建立的一种介于场路之间的计算方法，现已广泛应用于电磁系统的分析。使用这一方法，施加在发射线圈上的载荷为电压源，能够对电磁发射器的瞬态磁场和外部电路进行协同仿真，所得仿真结果能够更好地指导工程实践。笔者分析了方向可控电磁发射器的工作原理，建立了发射过程的场路耦合模型，并用有限元法对系统进行分析。

1 工作原理

方向可控电磁发射器的组成及工作原理如图1所示。

从图1可知，发射线圈由两个互相垂直的平面螺旋线圈A－A′和B－B′构成，它们分别与两个独立的高功率脉冲电源（电容器组C1、C2）和控制开关K1、K2相连，构成两个独立的放电回路。若K1、K2闭合，在脉冲大电流的作用下，发射线圈周围会产生变化的强磁场，拦截弹中将产生感应电流，磁场与感应电流相互作用，使拦截弹受到很大的电磁力，以一定的速度飞向目标。通过控制系统调节两个放电回路各自的放电延时t1和t2，便可控制拦截弹的飞行方向。线圈B－B′工作（t2＝t0），而线圈AA′不工作（t1＝∞）时，拦截弹将沿方向1飞行；而线圈A－A′工作，线圈B－B′不工作时，拦截弹将沿方向5发射。线圈A－A′和线圈B－B′同时工作时，若t1＝t2＝t0，拦截弹将沿方向3飞行；若t1＞t2，拦截弹将沿方向2飞行；若t1＜t2，拦截弹将沿方向4飞行。这样方向可控电磁发射器能在90°的扇形面内，对来袭弹丸进行拦截［3］。

2 三维场路耦合的数学模型

2.1 等效电路

电磁发射器场路耦合的等效电路如图2所示。

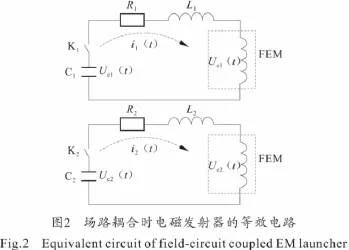
忽略发射线圈中的涡流，发射器放电回路的电路方程为：

式中：Uc1（t）、Uc2（t）为电容器组两端电压；i1（t）、R1、L1和i2（t）、R2、L2分别为线圈A－A′和B－B′控制电路中的电流、电阻和电感；Ue1（t）和Ue2（t）为发射线圈A－A′和B－B′在拦截弹中产生的感应电动势。

为求得Ue1（t）和Ue2（t），可沿发射器放电回路对电场强度进行线积分得：

式中：nc1，nc2分别表示发射线圈 A－A′和B－B′ 的匝数；sc1，sc2为发射线圈 A－A′和 B－B′ 的截面积；A1，A2为发射线圈A－A′和B－B′的矢量磁位；h1，h2为切向单位矢量。

将式（2）代入式（1），得到发射器两个放电回路的场路耦合方程。

2.2 磁场及涡流场的控制方程

方向可控电磁发射器的发射过程时间很短，只有1～3ms。在建立发射器的磁场及涡流场的控制方程时，作如下假设：

1）假定发射器的发射过程处于准稳态条件下。

2）忽略线圈和拦截弹在电磁力作用下的变形。

3）发射线圈、拦截弹及绝缘材料等全部为匀质线性材料。

在假设条件下，可将发射器模型的整个求解区域V分解为涡流区域V1和非涡流区域V2两部分［9］。其中，涡流区域为导电介质但不含源电流，指拦截弹区域；非涡流区域包括源电流区域和其他非导电介质，指发射线圈、底座、绝缘体和周围部分空气区域。根据Maxwell方程组及涡流场的似稳条件，在忽略位移电流、考虑拦截弹运动效应的情况下，用A、φ－A法描述的发射器工作过程的磁场及涡流场的控制方程为：

方程（3）和（4）与场路耦合方程组合在一起，即得到发射器三维瞬态磁场和涡流场的计算模型。由于计算模型中多为矢量方程，对这些方程进行解析求解是很困难的，本文采用有限元法通过数值仿真进行求解。

3 动态过程仿真

3.1 物理模型

发射线圈的材料为紫铜，两线圈各10匝，截面为矩形。拦截弹为厚度90mm的梯形体，材料为铝合金。发射线圈用弹性体材料浇注在底座中，底座材料为环氧树脂。图3所示为方向可控发射器各部分的截面参数示意图，各参数取值如表1所示。

3.2 仿真模型

考虑到发射器的对称结构，对其进行有限元分析时可只对一半进行建模。由于通过控制发射器放电回路的放电延时，可使拦截弹在90°的扇形面内沿任意一个方向运动。这里仅对拦截弹沿方向3（图1）运动即两个线圈同时放电的情况进行分析。

按编制的有限元程序建立发射器的三维场路耦合仿真模型如图4所示，它主要由外加电路和发射器的有限元模型两部分组成，发射器外部为空气区域。仿真时，电容器组的充电电压为3kV、电容量为2mF，拦截弹与发射线圈间的初始距离为2mm。

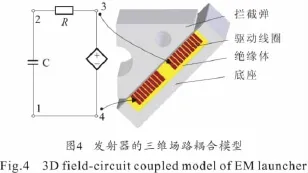
4 仿真结果分析

4.1 磁场分析

图5和图6分别为t＝0.5ms时，发射器中的磁场分布和拦截弹中的涡流分布。

由图5可知，发射线圈产生的磁场在拦截弹内发生明显削弱现象。在发射线圈所产生变化磁场的作用下，拦截弹内产生变化的涡流，也产生变化磁场。该磁场与发射线圈产生的磁场方向相反，从而排斥发射线圈的磁场进入拦截弹内部。

由图6可知，拦截弹的涡流区主要集中在底部，拦截弹底部中心部位的磁场感应强度最大。随着拦截弹与发射线圈距离的增大，沿拦截弹底部平面的法线方向，磁感应强度逐渐减小。磁感应强度的分布和强弱是影响拦截弹受力的重要因素，为提高发射过程中拦截弹的受力，在设计时，应当减小拦截弹与发射线圈间绝缘层的厚度。

4.2 拦截弹受力及动态特性分析

图7所示为仿真所得发射器放电回路中的电流波形。图8和图9分别为拦截弹的受力和速度随时间的变化规律。

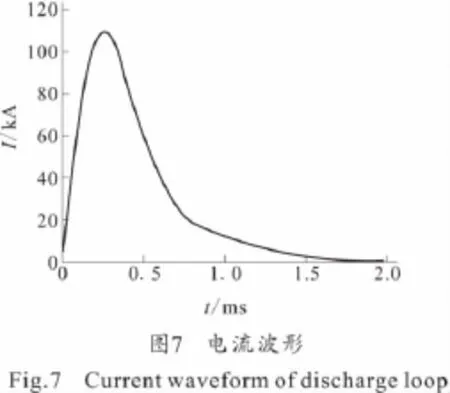
从图7～图9可知，在放电过程中，随着放电电流的变化，拦截弹所受的电磁力先增大后减小，在t＝0.27ms时达到峰值335.2kN，到1.0ms时几乎衰减到0。拦截弹的速度在前0.75ms的时间内迅速增加，之后随着拦截弹与发射线圈距离的增大，以及电容器组两端电压的减小，拦截弹所受的电磁力很小，速度变化很小，拦截弹所达到的最大速度为80.9m·s－1。要提高拦截弹的发射初速，应在发射线圈材料强度满足要求的前提下增大电流（电压）载荷，并使载荷在尽可能短的时间内达到峰值。

4.3 拦截弹的初始位置对其发射速度的影响分析

为了分析拦截弹的初始位置对拦截弹发射速度的影响规律，当拦截弹与发射线圈间的距离分别为4、6和10mm时，重复前述步骤对发射器的工作过程进行仿真，得到拦截弹的发射速度分别为73.2、59.7和32.6m·s－1。比较可知，当拦截弹与发射线圈的距离为2和10mm时，发射速度相差48.3m·s－1。随着拦截弹与发射线圈间距离的增大，拦截弹的速度迅速减小。因此，为了提高发射初速，在设计时应尽可能地减小拦截弹与发射线圈间的距离。

5 实验数据与仿真结果的比较

为了验证仿真结果的正确性，利用电磁发射实验系统，进行拦截弹的发射实验。图10所示为电磁发射实验装置的原理框图［5］。

从图10可以看出，实验装置主要脉冲电容器组（C1和C2）、高压整流硅锥（D1、D2、D3和 D4）、放电开关（S1和S2）、触发及控制电路、两个发射线圈、拦截弹、电流测量装置、电压测量装置、和速度测量装置组成。实验中，电容器组的电容参数、充电电压、发射线圈和拦截弹的结构参数及质量与仿真模型中相同，对两发射线圈同时加载，进行实验。

根据1组3次实验结果计算拦截弹发射速度的平均值为70.2m·s－1，而仿真结果为80.9m·s－1，与实验数据的相对误差为13.23%，从仿真结果与实验数据的对比来看，所建立的仿真模型所得结果基本准确。

6 结 论

分析了方向可控电磁发射器的工作原理，建立了发射器发射过程的场路耦合模型。用有限元法对发射器的发射过程进行了场路耦合分析，得到了发射过程中放电回路的电流波形、发射器的磁场和涡流分布，以及拦截弹所受电磁力、拦截弹速度和位移随时间的变化规律。此外，还探讨了拦截弹初始位置变化对拦截弹发射速度的影响规律。

利用电磁发射实验装置进行了拦截弹发射实验，实验数据与仿真数据比较结果表明：所建立的仿真模型所得结果基本准确。

（References）

［1］LI Zhi－yuan，MING Sun，FENG Ming.The finite elemnet analysis for the magnetic of the active EM armor projectile interceptor［C］.IEEE Proceedings of the 12th Symposium on Electromagnetic Launch Technology，Snowbird，Utah，America，2004：441－443.

［2］ZHENG Ping，LIU Yong，CHENG Shu－kang，et al.Research on the Passive EM Armor［C］.IEEE Proceedings of the 12th Symposium on Electromagnetic Launch Technology，Snowbird，Utah，America，2004：450－453.

［3］CAO Yan－jie，WANG Cheng－xue，WANG Hui－jin，et al.Simulation of EM launcher of active EM armor［C］.IEEE Proceedings of the 14th Symposium on Electromagnetic Launch Technology，Victoria，British Columbia，Canada，2008.

［4］王成学，曹延杰，邹本贵.主动电磁装甲发射过程研究［J］.电光与控制，2009，16（8）：93－96.WANG Cheng－xue，CAO Yan－jie，ZOU Ben－gui.Research on launching process of interception projectile in active electromagnetic armor［J］.Electronics Optics ＆Control，2009，16（8）：93－96.（in Chinese）

［5］CAO Yan－jie，WANG Hui－jin，WANG Cheng－xue，et al.Acceleration process of the interception projectile in active electromagnetic armor［J］.IEEE Transactions on Magnetics，2009，45（1）：238－241.

［6］STERZELMEIER K，VOLKER BROMMER，LAURENT.Active armor protection－conception and design of steerable launcher systems fed by modular pulsed－power supply units［J］.IEEE Transactions on Magnetics，2001，37（1）：238－241.

［7］STERZELMEIER K，BUDERER G，GAUTHIER－BLUM C，et al.Electromagnetic armor test facility with modular pulsed power conceptual design［C］.12th IEEE Int.Pulsed Power Conference，Monterey，CA，USA，1999.

［8］SPAHN＊ E，STERZELMEIER K，GAUTHIER－BLUM C，et al.50kJ Ultra－compact pulsed－power supply unit for active protection launcher systems［J］.IEEE Transactions on Magnetics，2009，45（1）：462－466.

［9］谢德馨，杨仕友.工程电磁场数值分析与综合［M］.北京：机械工业出版社，2008：17－21.XIE De－xin，YANG Shi－you.Numerical analysis and synthesis of engineering electromagnetic field［M］.Beijing：Mechanical Industry Press，2008：17－21.（in Chinese）