翼身组合体摇滚特性高速试验研究

陶 洋，赵忠良，杨海泳

（中国空气动力研究与发展中心，四川 绵阳 621000）

翼身组合体摇滚特性高速试验研究

陶 洋，赵忠良，杨海泳

（中国空气动力研究与发展中心，四川 绵阳 621000）

简要介绍了翼身组合体高速风洞自由摇滚实验技术的实验装置、实验方法、数据采集等。开展了翼身组合体大迎角下的摇滚特性研究，给出了典型的结果，研究结果表明随着模型迎角的增加，翼身组合体呈现不同的滚转运动形态，包括静态稳定、准极限环摇滚等。所研究的参数范围内后掠角对摇滚有较大影响，随着模型迎角的增加摇滚振幅呈现抛物线，马赫数的增加对最大摇滚振幅起抑制作用。

摇滚；翼身组合体；大迎角；准极限环；高速风洞试验

0 引 言

大迎角下翼身组合体将会出现绕体轴摇滚的非线性运动现象，人们称之为机翼摇滚（wing rock）。该现象的出现不仅限制了以翼身组合体为基本气动布局的现代飞行器的飞行包线，而且严重影响其大迎角飞行的机动操纵性能。因此机翼摇滚特性研究受到众多空气动力学学者的关注。

由于机翼摇滚现象的发生和飞行器几何外形密切相关，Ericsson基于大量的试验及计算结果分析将机翼摇滚分成3类，即：细长机翼摇滚（Slender Wing Rock）、常规机翼摇滚（Conventional－Wing Rock）和翼／体摇滚（Wing－body Rock）。

在研究方法上，由于摇滚主要以滚转振动为主（滚转振幅远比其它方向振幅大得多），绝大部分文献为避免复杂的全机外形干扰，重点探讨流动基本机理，以研究单自由度滚转的摇滚运动为主。

细长机翼摇滚是指：小展弦比、大后掠三角翼和部分翼身融合体上发生的摇滚现象。

常规机翼摇滚是指：直机翼与中等后掠角机翼产生的极限环振动形式的摇滚现象。这类摇滚和前面的细长机翼摇滚物理机理不同，在某种程度上可以认为其气动特性是由翼面上的二维流向运动所左右的，并和动态失速密切相关。

翼体摇滚是指：机翼和机身（包括前体）组合外形所发生的摇滚现象。显然，这一类外形更加接近真实飞行器，因此，其摇滚现象具有更加重要的实际意义。

试验结果表明：由前体涡诱导的翼／体摇滚往往比单独机翼前缘涡诱导的摇滚更加强烈。某典型战斗机的试验结果显示：只需要不到3个振动周期，即可发展成振幅为30°～40°的极限环振动（而对一个80°前缘后掠翼常常需要差不多10个周期）。在某种程度上，这是非常危险的状态，因为它没有足够的时间留给飞行员操纵飞行器从极限环振动中恢复到正常飞行状态。

目前针对三角翼的研究开展得较多，研究也比较深入，针对翼体摇滚问题的研究，由于问题的复杂性等原因，相应的研究开展得较少，本项研究主要针对翼体摇滚问题开展相关研究。

试验主要采用翼身组合体模型大迎角下的翼体摇滚特性进行了研究，研究的参数包括：不同的机翼形状，不同的翼位置，不同马赫数，不同迎角，给出了典型的结果。

1 试验设备和模型

1.1 风 洞

试验是在气动中心高速所的FL－23风洞中完成的。FL－23风洞系试验段横截面为0.6m×0.6m的直流暂冲式亚、跨、超声速风洞。试验马赫数范围为0.3～4.5，马赫数控制精度为±0.005。迎角范围为－10°～50°，试验段上下壁面为开孔率4.2%的60°斜孔壁，两侧为实壁［4］。

1.2 模 型

试验模型为翼身组合体模型。模型全长：504mm；模型展长：281.4mm；机身直径：50mm。模型迎角为0°时在风洞中的堵塞度约为0.6%，模型迎角为30°时在风洞中的堵塞度约为3.2%。

模型示意图以及其在风洞中安装情况见图1。

图1 试验模型Fig.1 Models of test

1.3 其它设备

自由摇滚装置采用精密机械球轴承支撑，通过联接装置与单支臂大迎角机构相联，通过12位绝对式轴角编码器来测量模型的角位移，测量精度可达0.088°，支撑装置中的微型电磁离合器用于控制模型的锁定及释放，实验数据的采集由PXI－4472B动态信号采集模块完成，最高采样频率为100kHz。

数据处理公式如下：以平均滚转角、滚转角均方根、减缩频率来表征自由摇滚运动的3个量，其具体处理公式如下：

滚转角均方根：

2 试验结果与讨论

试验中得到了包括不同的马赫数、不同迎角、不同机翼位置、不同机翼形状的翼身组合体模型滚转特性。试验马赫数范围0.3～0.7，迎角范围20°～40°，相应雷诺数范围0.65×107／m～1.29×107／m。

图2中给出了重复性试验结果，试验条件为30°后掠三角翼，M＝0.4，翼尖距离模型头部4D（D为模型直径），从图2可见试验结果的重复性精度较高，特别是在迎角35°和40°滚转角的均方根基本重合，在小迎角条件下滚转角的均方根存在一定差异。

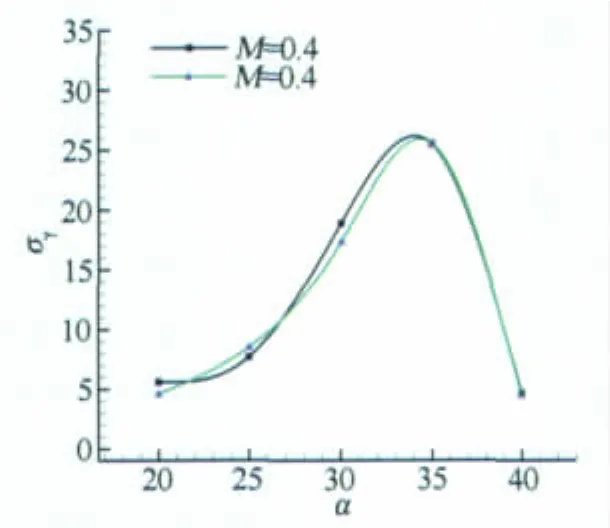
图2 试验重复性（30°后掠翼，M＝0.4，翼位置4 D）Fig.2 Repeatability of the test data

2.1 不同机翼外形对翼身组合体摇滚特性的影响

试验共加工5副机翼，分别为30°后掠角三角翼、50°后掠角三角翼、50°后掠角梯形翼、72°后掠角三角翼、30°带边条（72°）后掠翼。其中50°后掠角三角翼、50°后掠角梯形翼、72°后掠角三角翼三种机翼的翼身组合体在所研究范围内没有明显的摇滚现象发生，在所研究的参数范围内，对翼身组合体模型来说，较大的后掠角（大于50°）时无摇滚发生。30°后掠角机翼（钢制翼）在所研究迎角及马赫数范围内，具有较明显的翼体摇滚现象发生，30°带边条（72°）后掠翼会发生不规则的滚转运动（没有固定的频率），通过比较30°带边条（72°）后掠翼与30°后掠角机翼两种模型的摇滚特性可以发现，边条翼的引入对机翼摇滚起抑制作用。其后对迎角及马赫数的研究主要基于30°后掠翼，机翼头部距离模型头部4倍直径的位置。

2.2 不同迎角对翼身组合体摇滚特性的影响

迎角的影响主要针对30°后掠翼4D位置模型开展。在较小的迎角条件下（M＝0.3及0.4时迎角小于25°）试验模型只出现围绕平衡滚转角的微振，滚转角的均方根在5°～10°之间，也没有明显的摇滚频率，考虑其形成的原因可能主要是由于气流的湍流脉动所引起，在迎角30°、35°、40°三种条件下形成具有明显周期的极限环摇滚，其中在迎角35°时其摇滚的滚转角的均方根最大，并且摇滚振幅比较均匀。图3给出了30°后掠翼迎角为35°时的一个典型的摇滚结果。

图3 自由摇滚时间历程Fig.3 History of free to roll

2.3 不同马赫数对翼身组合体摇滚特性的影响

以30°后掠翼，翼位置4D模型状态的翼身组合体为基础开展马赫数对翼身组合体摇滚特性影响的研究，图4给出了模型在不同马赫数条件下的摇滚特性，由图可见，M＝0.3与M＝0.4情况下的摇滚特性类似，均在α＝35°附近出现峰值，而马赫数M＝0.5与M＝0.6条件下的峰值发生在α＝30°附近，M＝0.6比M＝0.5时略大，并且摇滚幅值的均方根较小为σ＝16°左右，当M＝0.7时，可能由于出现了激波的影响，其摇滚滚转角的均方根随迎角分布与前几个状态有所不同，在迎角20°～35°范围内呈现抛物线型分布。在同一马赫数条件下，摇滚运动的频率基本相同，从M＝0.3～0.7这一过程中，其摇滚频率分别为4.3、6.0、8.0、9.2、10.3，总的来说摇滚频率是随着马赫数的增加而增加的。图5给出了摇滚频率及摇滚减缩频率随马赫数变化的示意图。

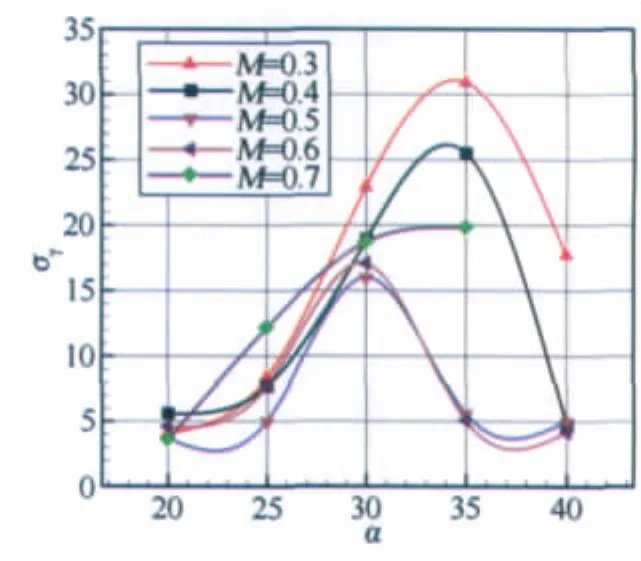
图4 不同马赫数下的摇滚振幅（30°后掠翼，M＝0.4，翼位置4 D）Fig.4 Roll amplitude at different mach numbers

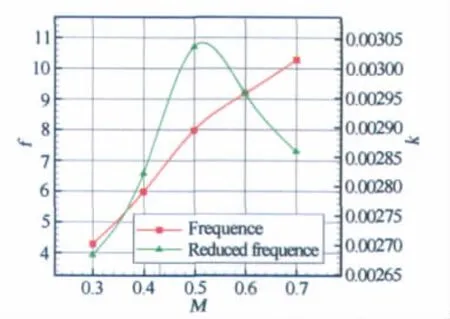
图5 摇滚频率及减缩频率随马赫数变化曲线Fig.5 Frequency and reduced frequency at different Mach numbers

2.4 不同机翼位置对翼身组合体摇滚特性的影响

在30°后掠翼，M＝0.4，迎角35°条件下研究不同机翼位置对翼身组合体摇滚特性的影响，图6给出了在该条件下不同机翼位置（3D、4D、5D）的滚转角均方根，从图示可见从3D位置开始随着机翼位置的后移滚转角的均方根开始减小，说明头尖涡对机翼的影响逐渐减小。

2.5 翼体摇滚形成机理的空间流态分析

图7给出了基于CFD的流场结构，所给状态为M＝0.4，γ＝20°，α＝35°，从翼面流动来看，下沉一侧的分离涡涡核更加靠近机翼表面，同时从机翼表面的压力分布来看也是提供的回复力矩。也可以看成存在偏离一侧机翼方向的侧滑角，这也将导致下沉一侧的分离涡涡核距离物面较近，提供模型的回复机制。

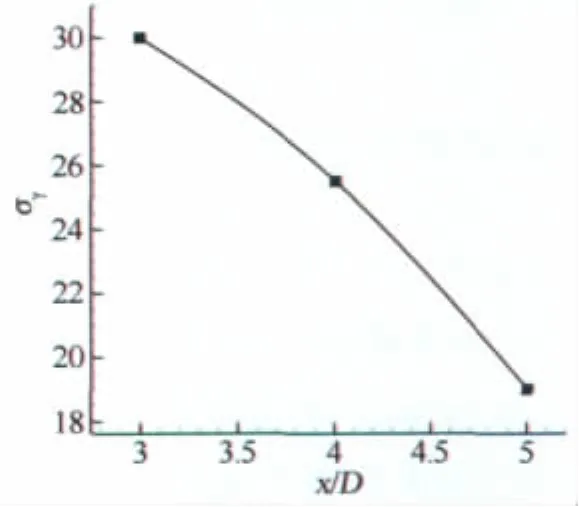
图6 机翼位置对滚转角均方根的影响Fig.6 Mean square root of roll amplitude with different wing positions

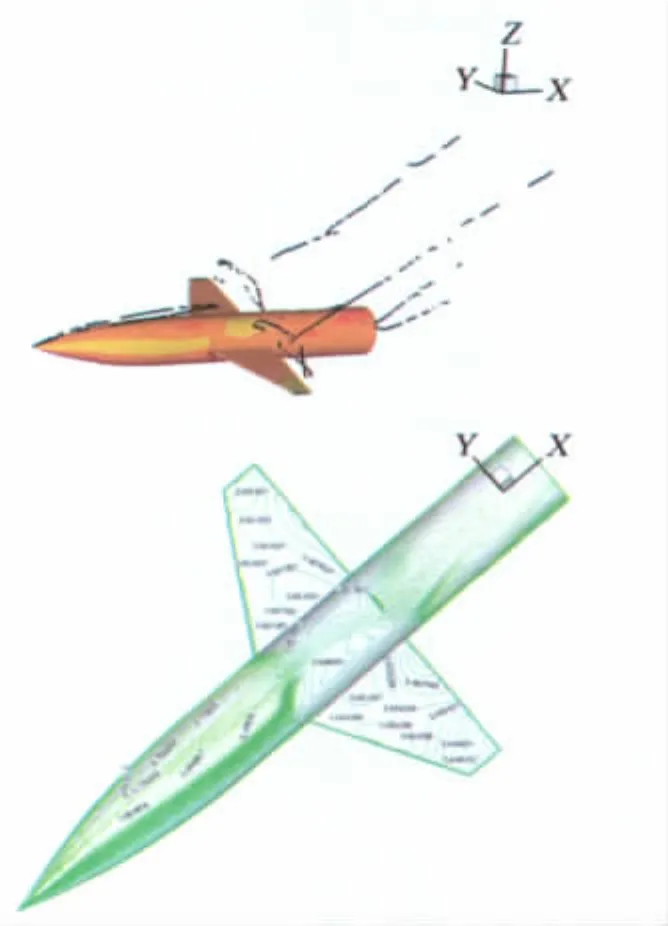
图7 M＝0.4，γ＝20°，α＝35°空间流态Fig.7 Space flow at M＝0.4，γ＝20°，α＝35°

总的来说翼体摇滚形成需要的两个条件为回复机制（主要存在于大滚转角条件）与偏离机制（主要存在于平衡滚转角附近），其中回复机制可以通过上面两种流态的分析给出，而偏离机制与流动相对于运动相对滞后有关，需要进一步开展动态的流态观察来加以分析。

3 结 论

通过对翼身组合体自由摇滚试验研究可以得出以下结论：

（1）本次试验数据重复性较好，数据质量较高，试验结果规律合理；

（2）较大的后掠角对翼体摇滚起抑制作用，加装边条翼也可以部分抑制翼体摇滚现象发生；

（3）翼体摇滚随迎角的增加幅值增加，达到峰值后开始减小；

（4）随着马赫数增加，摇滚振幅峰值对应迎角减小，形成极限环摇滚后随马赫数增加频率而增加，减缩频率在M＝0.5时存在峰值。

［1］Alain Pelletier.Dynamic behavior of an 80／65doubledelta wing in roll［R］.AIAA－98－4353.

［2］ERISSON L E.Wing rock generated by forbody vorteces［J］.J.Aircraft，1989，26（2）.

［3］伍开元.面向先进飞行器设计的非定常空气动力学［J］.流体力学实验与测量，1997，11（2）：14－18.

［4］樊开导.0.6m×0.6m 跨超声速风洞性能与使用CARDC－2［R］.1990.

［5］TRICKEY C M，EDWARDS J A，SHAW S.Experimental and computational assessment of the dynamic stability of a supersonic square section missile［R］.AIAA 2004－5454.

［6］袁先旭.非定常流动数值模拟及飞行器动态特性分析研究［D］.中国空气动力研究与发展中心博士学位论文，2002.

［7］陶洋，赵忠良，杨海泳，等.方形截面导弹动态摇滚特性研究［J］.实验流体力学，2009，23（2）：50－53

［8］刘伟，张涵信.细长机翼摇滚的数值模拟及物理特性分析［J］.力学学报，2005，37（4）：385－392.

陶 洋（1980－），男，湖北麻城人，博士。研究方向：非定常空气动力学。通信地址：四川省绵阳市中国空气动力研究与发展中心（621000）

Investigation on wing rock of wing－body configuration at high speed wind tunnel

TAO Yang，ZHAO Zhong－liang，YANG Hai－yong
（China Aerodynamics Research and Development Center，Mianyang Sichuan 621000，China）

The free to roll test technique in high speed wind tunnel is presented in this paper，including test apparatus and test methods as well as data acquisition.A test investigation of the dynamic behavior of an wing－body configuration at high angle of attack was conducted.Dynamic motions were obtained on the wing－body configuration that was free to rotate about its longitudinal axis，different dynamic rolling motions were observed depending on the angle of attack of the model sting.Two dynamic regimes included damped oscillations，quasi－limit－cycle rock motion.The sweep－back angle of the wing－body configuration have significant influence on the dynamic behavior in roll.The amplitude of the wing rock is parabolic with the angle of attack，and with the increase of Mach number the biggest wing rock amplitude are restrained.

rock；wing－body configuration；high angle of attack；quasi－limit－cycle；high speed wind tunnel test

V211.3

A

1672－9897（2011）06－0045－04

2011－01－14；

2011－07－29

国家自然科学基金项目（10972233）