覆冰拉线直流输电塔驰振结构动力特性分析

祝 贺，姜武超，米 江

(1.东北电力大学建筑工程学院，吉林吉林132012;2.吉林市供电公司，吉林吉林132011;3.四川电力公司超特高压运行检修公司，四川南昌615000)

由于高压直流输电在远距离大容量输电和电力系统联网方面具有明显的优点，直流输电工程已成为我国“十二五”电网规划的重要组成部分。

直流输电线路担负着传导电流、输送电能的重要任务，其安全性与可靠性受到全社会的日益关注。而直流输电塔终于作为输电线路的重要组成部分，承担导地线及相应风、冰、地震载荷。因此，塔结构的稳定程度直接影响输电安全。

在特殊地形下，采用拉线直流塔不可避免，在外载荷作用下，必须考虑拉线和塔身相互作用以及拉线非线性影响下的结构振动。动力风载荷使塔线结构产生振动，而结构的振动反过来又使结构上的风力随结构振动速度变化而变化。这种由结构的运行而产生的附加动载荷称为空气动力阻尼力，当空气动力阻尼力为负值并与结构本身阻力相抵消时，由于在结构振动中产生负阻尼引起振动的发散，即结构的驰振，结构的驰振是一种动力失稳式振动，将导致结构破坏。作为特殊情况，覆冰是拉线直流塔产生驰振的诱因之一。覆冰情况下，拉线直流塔除受风激励会产生强迫振动以外，还可能由于结构本身振动而引起风来流的方向和大小改变，从而引起塔结构和拉线界面的平均升力系数和阻力系数变化，在一定风向和临界风速下，空气动力产生的负阻尼大于正阻尼，拉线直流塔将产生大幅度振动，严重时将发生结构破坏性失稳。

国内外关于输电线路的驰振研究都集中在导线和塔结构的独立研究，未涉及拉线与塔结构的塔线体系［1-6］。为此本文首先分析拉线直流塔产生驰振的原因，继而建立覆冰拉线驰振数学模型和直流输电塔结构振动数学模型，最后通过算例研究拉线覆冰直流塔驰振动力特性。

图1 驰振判别示意图

1 驰振判别依据

如图1，风来流相对于结构的攻角为α，由于阻力系数和升力系数都与风向有关，因此阻力和升力分别表示为:

在y方向这些力的投影合力为:

单自由度系统的运动微分方程为:

将Fy(α)在α=0附近展开，有:

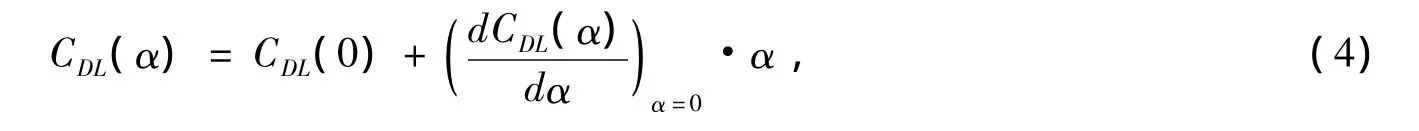
由(2)式得:

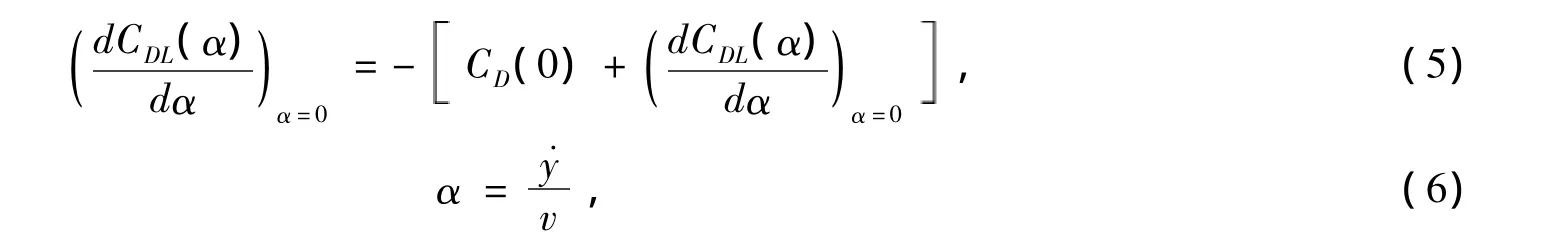
因此式(3)可写成:

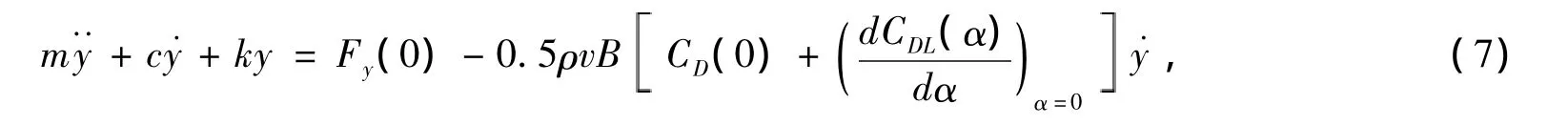
将上式改写成:

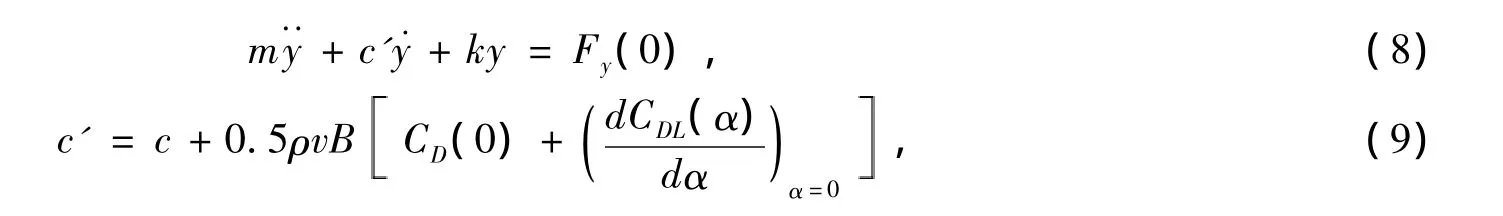
式中:第一项c为结构阻尼系数，第二项为空气动力阻尼系数。

当阻尼系数c'=0时，振动随时间减弱，结构稳定;当c'＜0时，振动将逐渐无限增大，出现结构失稳现象，因此c'=0是判断结构稳定状态的临界值。

因为是正值，结构失稳情况下，空气动力阻尼系数必须小于零，因此有:

上式作为判别结构驰振发生的必要条件。

2 覆冰拉线驰振数学模型

图2 拉线覆冰驰振模型

分析拉线覆冰引发驰振响应的基本假设:(1)假设垂直于风力方向上的运动产生气动力;(2)拉线覆冰后的截面在一段长度内保持不变［7］。计算模型见图2。

拉线在覆冰情况下，将形成不规则截面，可能产生驰振，由式(9)，令c'=0，得到驰振的临界风速、质量参数、空气动力参数分别为:

由式(4)和式(6)，将dCDL(α)展开:

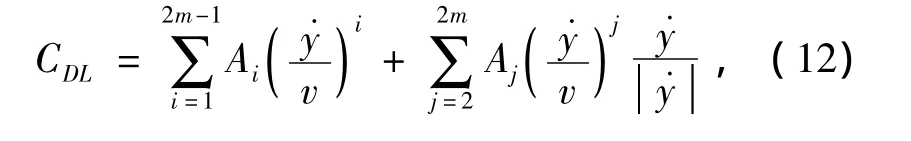
式中，i为奇数项，j为偶数项。

将上式代入式(3)和式(6)，得拉线运动方程为:

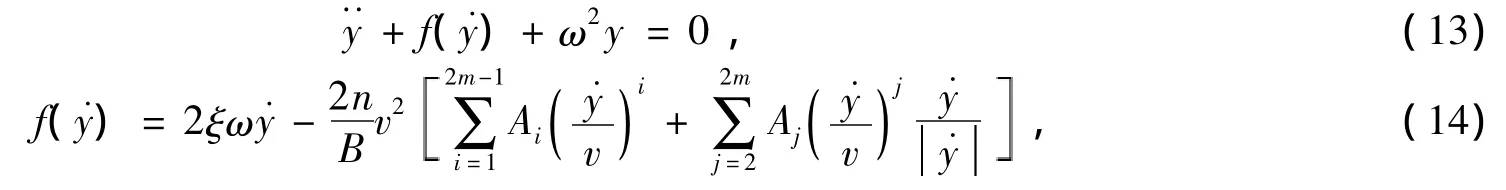
设产生驰振的拉线阻尼系数为c1，其余拉线阻尼系数为c2、c3、…、cn-1，塔结构阻尼为cn，则拉线驰振位移为:)

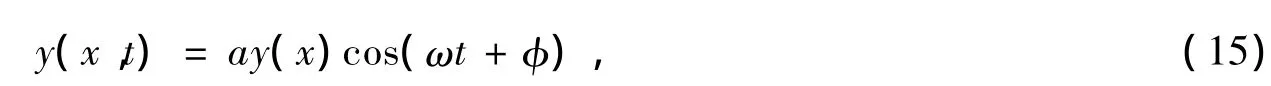
式中，a为垂直于拉线的振幅。塔结构位移为:

则气动力对驰振拉线所做的功为:

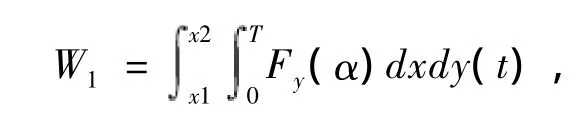
式中:T为驰振拉线振动周期，Fy(α)为激振力在y方向的投影合力，由式(2)求得;x1、x2分别为拉线覆冰上下边界范围。

3 覆冰下直流塔风激振动方程

覆冰下直流塔风激振动方程为:

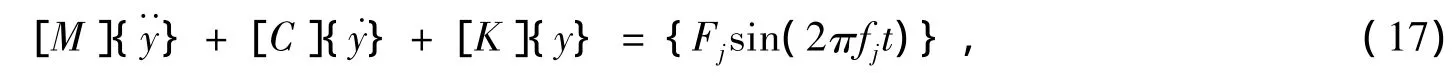
采用振型分解法，y(z，t)分解为:

将上式代入式(17)，考虑振型正交性及阻尼正交性的假定，并考虑稳态周期振动，得到结构第j阶振型位移为:

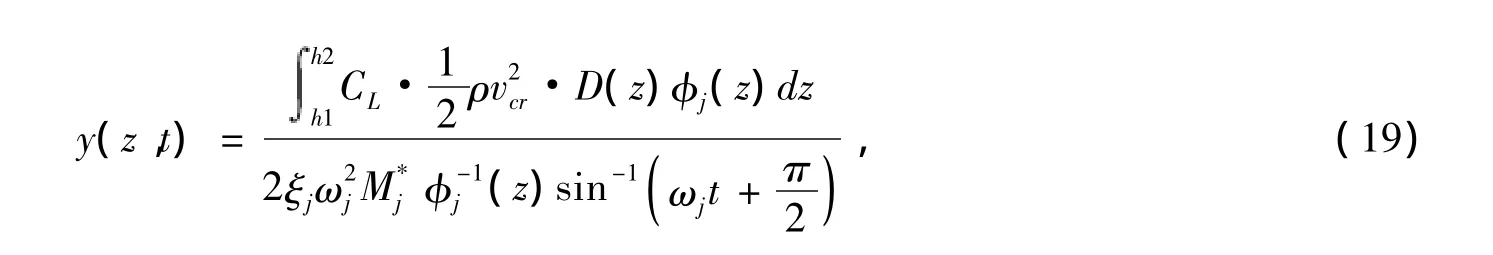
4 仿真算例

600 kV拉线直流塔，塔高40 m，采用四根拉线增强线路稳定，三维模型见图3。计算求得结构前四阶振动频率分别为:0.174、0.237、0.291、0.302 Hz，在软件ANSYS中改变局部拉线截面形状模拟拉线覆冰时截面形状，对拉线直流塔施加动态风载荷［8］，风速时程曲线见图4。

图3 拉线直流塔三维模型

图4 风速时程曲线

求得拉线直流塔在覆冰情况下前32阶振型，对于拉线直流塔来讲，前四阶振型为主要振型，列出见图5。

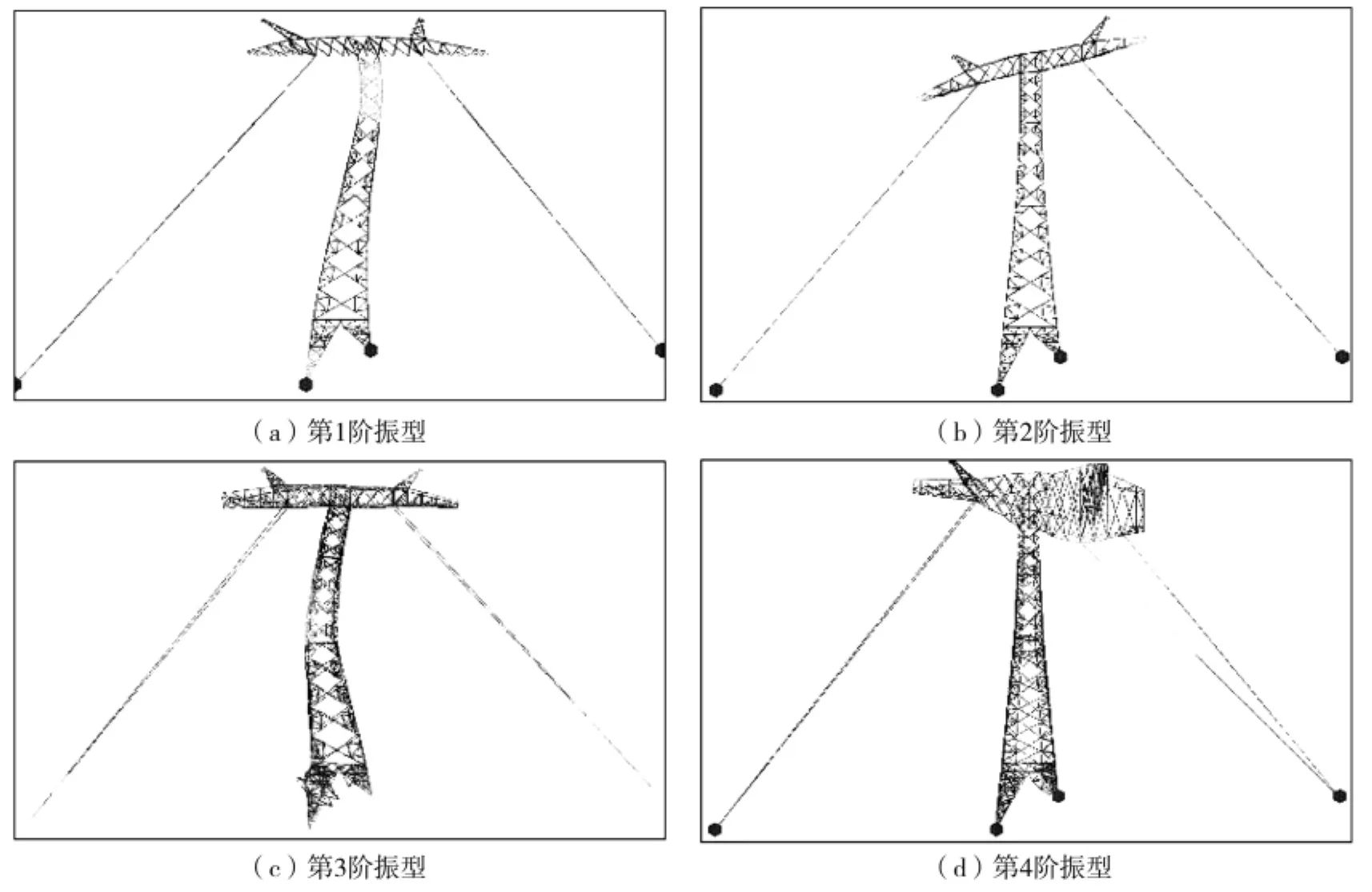
图5 拉线直流塔前四阶振型

由图5(a)，拉线直流塔第1阶振型表现为塔身侧向弯曲和左侧拉线伸长;由图5(b)，拉线直流塔第2阶振型表现为塔头横向倾倒和边横担扭转;由图5(c)，拉线直流塔第3阶振型表现为塔腿扭曲、塔身扭转;由图5(d)，拉线直流塔第4阶振型表现为塔横担扭转和右侧拉线出现大变形。

在软件中对拉线直流塔加载并完成动力特性分析，提取塔头节点10的动力特性参数见图6。

图6 塔头节点10的位移和加速度时程曲线

5 结 论

本文分析拉线直流塔产生驰振的原因，分别建立了覆冰拉线驰振数学模型和直流输电塔结构振动数学模型，得到以下结论:

(1)通过理论分析和仿真计算，证明覆冰对拉线和塔结构都存在驰振诱因;

(2)拉线覆冰驰振对塔结构风振存在影响;

(3)本文分别建立了覆冰下拉线和塔结构的驰振数学模型，为今后建立拉线和塔结构的联合数学模型奠定了基础。

［1］顾明，马文勇.两种典型覆冰导线气动力特性及稳定性分析［J］.同济大学学报，2009，37(10):1328-1329.

［2］苑吉河，蒋兴良，易 辉，等.输电线路导线覆冰的国内外研究现状［J］.高电压技术，2003，30(1):45-49.

［3］郭应龙，李国兴，尤传永.输电线路舞动［M］.北京:中国电力出版社，2003.

［4］Macdonald J H G，Larose G L.A unified approach to aerodynamic damping and drag/lift instabilities，and its application to dry inclined cable galloping［J］.Journal of Fluids and Structures，2006，22(2):229 - 230.

［5］Yu P，Popplewell N，Shah A H.Instability trends of inertially coupled galloping:PartⅡ:Periodic vibrations［J］.Journal of Sound and Vibration，1995，183(4):679 -681.

［6］李万平.覆冰导线群的动态气动力特性［J］.空气动力学学报，2000，18(4):413-420.

［7］BlevinsR D.流体诱发振动［M］.北京:机械工业出版社，1981.

［8］祝贺，徐建源.基于多点卡曼谱输入的输电塔脉动风数值模拟［J］.华东电力，2008，36(9):14-16.