蚁群算法在输电工程工期成本优化中的应用

屈成忠，马瑞枫，刘卫星，马晓东

(1.东北电力大学建筑工程学院，吉林 吉林 132012;2.元宝山发电有限责任公司，内蒙古 赤峰 027000)

自从M.Dorigo在1991年首次提出蚁群算法(ant colony algorithm)之后，因其能将问题求解的快速性、全局优化特征以及有限时间内答案的合理性结合起来的特点，为世界各地研究工作者广泛关注，该算法现己被大量应用于数据分析、机器人协作问题求解、电力、通信、水利、采矿、化工、建筑、交通等领域。

在国外，Song等人提出一种蚁群搜索方法用以处理因多目标约束引起的热量与能量扩散问题[1]。RACZYŃSKI等人将蚁群算法应用于解决因Lennard-Jones现象导致的原子相互作用的最小势能问题[2]。Lenin等人将蚁群算法应用于无功功率的优化和电力系统的电压控制中[3]。SLIMANI等人将蚁群算法用于电力系统的优化能量流问题，以使总的热能损耗降到最低[4]。Dréo等人提出了“持续作用蚁群算法”以处理连续函数多目标最小化问题[5]。Randall将平行分解技术应用于蚁群算法中，以使旅行销售问题的处理更加快捷、有效[6]。

在国内，康莉等人提出一种新的非线性多目标跟踪方法实现对单目标的跟踪，使蚁群算法适用于解决数据关联问题[7]。高尚等人提出了求解旅行商问题的多样信息素的蚁群算法[8]。马文霜等人通过对ACS－3－opt算法的改进，提出一种蚁群改进算法，用于大中型规模TSP问题的求解[9]。李梅娟等人设计一种改进的蚁群算法，用于自动化仓库固定货架拣选作业问题的解决[10]。康莉等人提出了一种新的基于蚁群算法的多目标跟踪方法:通过将多目标跟踪中的数据关联问题表示为具有约束条件的优化问题，用蚁群算法对该优化问题求解得到最优关联[11]。梁云川等人提出了一种基于子集类蚁群模型的属性相对约简算法以处理粗糙集属性约简问题[12]。

输电工程中的工期—成本优化的目的是为了寻求工期缩短而直接成本最少，对于输电工程施工过程中的成本控制、工期控制、资源管理具有极其重要的作用。本文应用蚁群算法实现对输电线路施工进行工期－成本优化。

1 工期－成本优化数学模型

工期－成本优化是在关键线路上选择赶工成本增率最低的工序或工序组合，通过缩短总工期，并把每次缩短工期后的工程的直接成本和间接成本叠加得到一系列工期和成本均不相同的方案。

工期－成本优化涉及两类工程实际问题:允许工期条件下工程最低成本，规定工期条件下最低成本。

(1)允许工期条件下，最低成本数学模型

工程项目的直接成本随着工期延长而减少，间接成本随着工期延长而增加，因而项目的总成本随着工期的延长必然出现一个先减后增的过程，确定最低成本的数学模型如下:

式中:TC为项目的总成本，是项目的直接费用和间接费用之和;DC为项目的直接费用，由项目的所有活动的直接费相加得到;IC为项目的间接费用，与项目工期有关的费用;fi(di)为工作i的持续时间与直接费用之间的函数，可以是线性的，也可以是非线性的;di为工作i的持续时间;e为项目的间接费用率，是一个常数;为极限状态下工作的持续时间;为正常状态下工作的持续时间;tj为工作j的结束时间;ti为工作i的结束时间;P(j)为工作j的紧前工作集合;TN为项目的实际工期;TD为项目的计划工期。

公式(2)的约束是对工作持续时间的约束，保证活动的持续时间在允许的工期范围之内;公式(3)的约束是工序约束，保证活动的施工顺序符合逻辑关系。

(2)规定工期条件下，最低成本数学模型

如果项目按正常条件施工会超过规定工期，不能满足工期要求，就需要对工期进行压缩，也就是工期固定、成本最低的数学模型如下:

式中各物理量的含义同上。

若TN固定，间接成本变成一个常数，公式(4)eTN中的项可以去掉，不会影响求解结果，这样目标函数变为:

2 蚁群算法设计

蚁群算法是一种基于种群的启发式仿生进化算法，算法中蚂蚁的行为模拟生物界中的蚂蚁觅食行为。单只蚂蚁在所通过的路径上留下信息素，其他蚂蚁则根据信息素选择觅食线路。蚂蚁在选择路径时会选择其中一条信息素浓度最大的线路。线路质量好坏与信息素多少相关。路线上的信息素随时间增加而逐渐减少，避免陷入局部最优解。

在进行线路搜索时，蚂蚁通过转移概率、选择节点来完成整个旅程。搜索开始时，每条线路分配少量的相同信息素。每只蚂蚁通过启发因子和信息素因子选择节点。启发因子为ηij，信息素因子为τij。蚂蚁应用Pseudo-Random-Proporlional法则选择下一个节点。蚂蚁在节点集合S中选取未曾选取的节点Si，使得下列式子值最大:

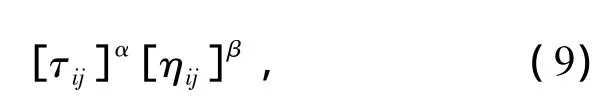
式中:α为路径的相对重要性，β为能见度的相对重要性，α和β均是常量，且α≥0、β≥0。

从集合S中所选取的节点由转移概率准则决定:

转移概率是启发因子和信息素因子之间平衡的结果。由启发因子可知:越近的节点，所需时间越短，被选择的概率越大。依据信息素因子，如果线路(Si，Sj)上交通量很大，则执行自催化过程。

启发因子ηij可由下式算出:

式中:f(xj)为蚁群中任意一个蚂蚁Xj的函数。

Si和Sj之间的信息素由下式定义:

通过蚁群算法进行输电工程工期－成本优化的算法流程见图1。

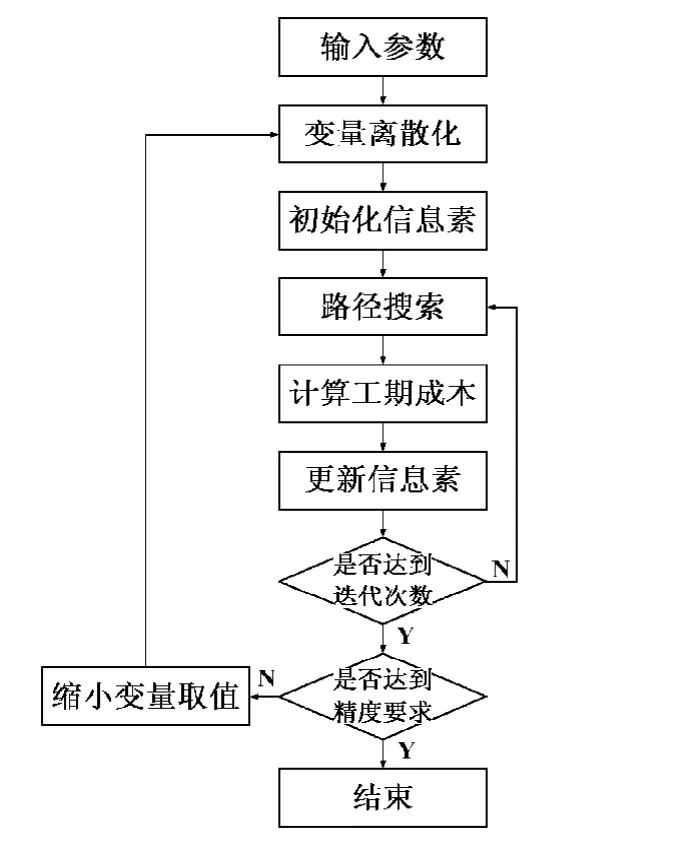
图1 算法流程图

图2 网络计划图

3 算 例

选取500 kV输电线路施工为例，其网络计划见图2，各工序实施方案、持续时间和直接费用见表1。工地每天的管理费为2500元/天。

按照上述提出的算法编制程序，设置程序参数如下:p=0.9，迭代次数为20，蚂蚁数为40，以程序运行10次的结果作分析数据，表2表示10次运行结果。

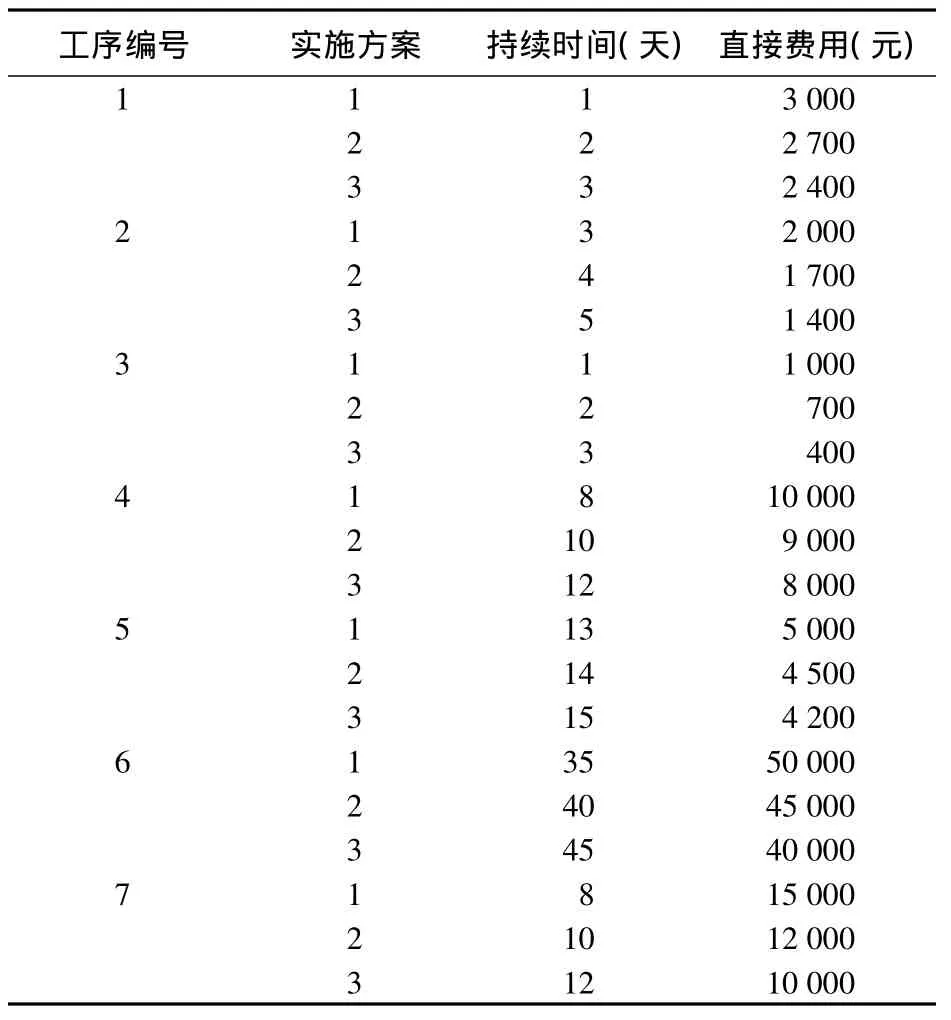
表1 实施方案、持续时间、直接费用表

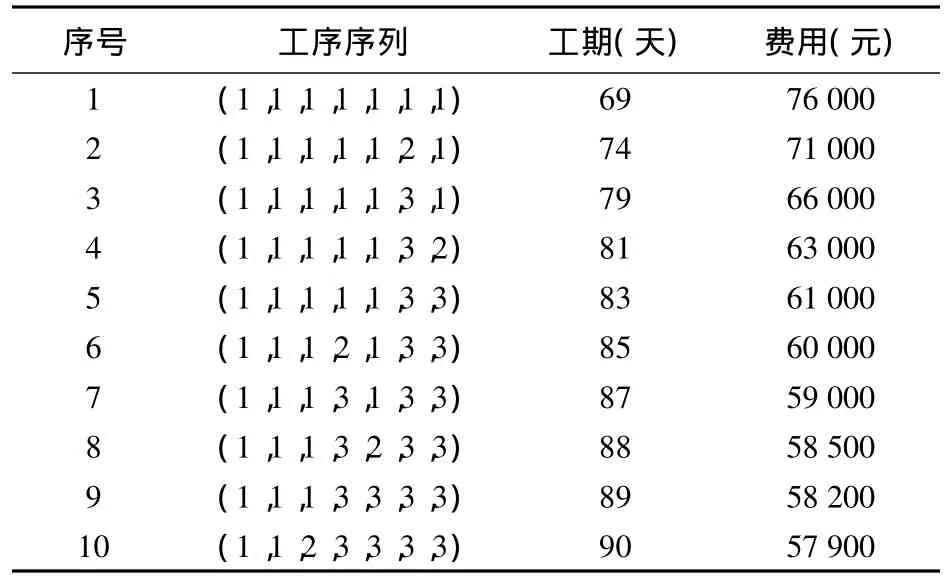
表2 分析结果

由表2可见，通过蚁群算法进行工期－成本优化时，可以按照优化序列结果，依据施工单位的经济、技术、设备、人员配置情况，在遵照与建设单位签订的施工合同条款的前提下，选取最优的施工方案。

4 结 论

本文研究了输电工程施工中的工期－成本优化问题应用蚁群算法进行求解的问题。首先分析了工期－成本优化问题中所涉及的两类工程实际问题的优化模型的建立，对蚁群算法进行分析并将其应用于所建的优化模型中，选择实际输电线路工程运用所确定的方法进行工期－成本优化，优化结果表明蚁群算法对于输电工程施工中的工期－成本优化是可行的。

[1]Y.H.Song，C.S.Chou，T.J.Stonham.Combined Heat and Power Economic Dispatch by Improved Ant Colony Search Algorithm[J].Electric Power Systems Research，1999，52(2):115 －121.

[2]P.RACZYŃSKI，Z.GBURSKI.The Search for Minimum Potential Energy Structures of Small Atomic Clusters Application of The Ant Colony Algorithm[J].Materials Science － Poland，2005，23(3):599 －606.

[3]K.Lenin，M.R.Mohan.Ant Colony Search Algorithm for Optimal Reactive Power Optimization[J].SERBIAN JOURNAL OF ELECTRICAL ENGINEERING，2006，3(1):77 － 88.

[4]Linda Slimani，Tarek Bouktir.An Ant Colony Optimization for Solving The Optical Power Flow Problem in Medium － Scale Electrical Network[J].Journal of Electrical Engineering，2006，6(1):10 －15.

[5]J.Dréo，P.Siarry.Continuous Interacting Ant Colony Algorithm Based on Dense Heterarchy[J].Future Generation Computer Systems，2004，20(5):841－856.

[6]Marcus Randall.A Parallel Implementation of Ant Colony Optimization[J].Journal of Parallel and Distributed Computing，2002，62(9):1421－1432.

[7]康莉，谢维信，黄敬雄.基于SIS框架和蚁群算法的非线性多目标跟踪[J].电子与信息学报，2008，30(9):2148－2151.

[8]高尚，孙玲芳，侯志远，杨静宇.基于多样信息素的蚁群算法[J].计算机科学，2006，33(10):160－162.

[9]马文霜，张洪伟.基于改进ACS－3－opt蚁群算法的TSP[J].计算机工程，2008，34(19):200－203.

[10]李梅娟，陈雪波，刘臣奇.基于改进蚁群算法拣选作业优化问题的求解[J].计算机工程，2009，35(3):219－221.

[11]康莉，谢维信，黄敬雄.基于蚁群算法的多目标跟踪方法[J].系统工程与电子技术，2008，30(9):1782－1784.

[12]梁云川，李德玉.基于子集类蚁群模型的属性相对约简算法[J].计算机科学，2008，35(1):147－150.