齿谐波绕组感应电动势波形快速计算

夏永洪， 王善铭， 黄劭刚， 邱阿瑞

(1.清华大学电力系统及发电设备控制和仿真国家重点实验室，北京 100084;2.南昌大学信息工程学院，江西 南昌 330031)

0 引言

齿谐波励磁的混合励磁永磁同步电机基本原理是将气隙中的齿谐波磁密在转子齿谐波绕组中感应的齿谐波电动势，整流后提供给电机的励磁绕组，以实现气隙磁场的调节。与其他混合励磁永磁电机相比［1－4］，齿谐波励磁的混合励磁永磁同步电机进一步提高了材料的利用率和电机的功率密度。

对于齿谐波励磁的混合励磁永磁同步发电机，快速地计算出转子齿谐波绕组的感应电动势波形对于把握齿谐波励磁系统的空载和负载性能非常关键。

电磁场有限元法可以方便地考虑电机磁路结构和磁路饱和的影响，因此，在电机设计和性能分析中得到了广泛的应用［5－10］。文献［5］应用场路耦合时步有限元法对一台永磁同步电动机的动态性能进行了仿真分析。文献［6－7］采用将电机的多回路方程与有限元方法相结合的方法对一台交直流混合供电同步发电机空载电压波形和稳态性能进行了计算和分析。应用上述文献中所述的方法可以计算得到齿谐波绕组感应电动势波形，但需要经历电机瞬态过程，计算时间长。

实际上，在电机设计阶段往往更关注计算电机的稳态性能。文献［8－9］基于有限元法对一台同步发电机的稳态电磁场进行了计算，得到了同步发电机的电枢绕组空载电压波形。文献［10］基于有限元法对一台三次谐波励磁的同步发电机的稳态电磁场进行了计算，得到了同步发电机基波绕组和三次谐波绕组空载特性曲线以及三次谐波绕组电压波形。由电机理论可知，对于齿谐波励磁的混合励磁永磁同步发电机，当转子励磁磁动势相对定子每转过一个定子齿距，励磁磁动势所遇到的磁阻就重复一次。因此，通过求解一个定子齿距内定转子不同位置下的稳态电磁场，便可计算出转子齿谐波绕组的感应电动势波形。本文通过分析定子齿谐波磁导和转子齿谐波绕组节距的特点，对转子齿谐波绕组的感应电动势波形计算提出了进一步简化，并详细分析了其简化原理和计算思路，最后对一台齿谐波励磁的混合励磁永磁同步发电机进行了计算和实验。

1 简化原理

将坐标放在定子上，定子开槽时，定子齿谐波磁导沿圆周方向的变化，用电角度可以表示为

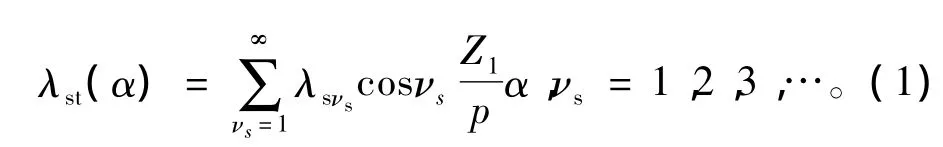
式中:α为电角度，其坐标原点在定子槽中心线上;νs为定子齿谐波磁导的阶数，νs=1时，称为定子一阶齿谐波磁导，νs=2时，称为定子二阶齿谐波磁导，依此类推;Z1为定子槽数;p为极对数;λsνs为定子各阶齿谐波磁导幅值。

电机空载运行时，气隙磁场由转子励磁磁动势产生，对于正常结构的转子，励磁磁动势中只含有基波和奇数次谐波。d轴与定子槽中心线对齐时为起始时刻，并将励磁磁动势变换到定子坐标系下，可以表示为

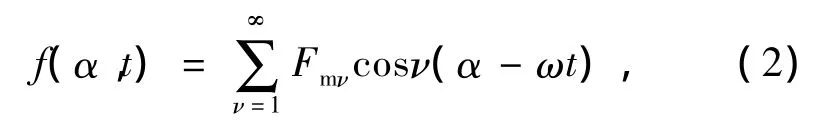
式中:Fmν为ν次谐波磁动势幅值，ν为奇数;ω为电机旋转的电角速度。

电机负载运行时，定子三相对称电枢绕组产生的合成磁动势中除了三相合成基波磁动势外，还含有其他高次谐波磁动势，其中三相合成基波磁动势占主导。对于同步电机，三相合成基波磁动势的旋转速度大小和转向与转子相同，因此，定子三相对称电枢绕组产生的三相合成基波磁动势作用在定子齿谐波磁导上引起的次齿谐波磁密，在转子齿谐波绕组中感应出次齿谐波电动势，即转子齿谐波绕组电动势波形中除了有一阶齿谐波电动势外，还包含有其他各阶齿谐波电动势。

当νs为偶数时次齿谐波磁密在构成转子齿谐波线圈的两根导体中感应的偶数阶次的齿谐波电动势在相位上基本相同，即对一个齿谐波线圈，合成后的偶数阶次齿谐波电动势很小，因此，忽略转子齿谐波绕组中偶数阶次的齿谐波电动势不会带来太大的误差。

此外，当电机定子斜槽，且斜1/2个定子齿距时，转子齿谐波绕组中的偶数阶次的齿谐波电动势的斜槽系数为0，即转子齿谐波绕组不存在偶数阶次的齿谐波电动势。

综上所述，在忽略转子齿谐波绕组中偶数阶次的齿谐波电动势或者转子齿谐波绕组中不存在偶数阶次的齿谐波电动势的情况下，即相当于不考虑定子齿谐波磁导中的偶数项，认为齿谐波磁导中只存在奇数项，则在1个定子齿距内，齿谐波磁导的波形在前后1/2个定子齿距内的分布是关于奇对称，因此，只需计算1/2个定子齿距内定转子不同位置下的电磁场，得到1/2个定子齿距内转子齿谐波绕组磁链的变化波形，即半个周期内的转子齿谐波绕组磁链波形，利用奇对称性，就可以获得转子齿谐波绕组在一个周期内磁链变化波形，从而快速地计算出转子齿谐波绕组的感应电动势波形。

2 感应电动势波形计算

将电机的1/2个定子齿距分成n等份，利用二维电磁场有限元法，计算1/2个定子齿距内定转子n不同位置下的电磁场，获取转子槽口在不同位置下的矢量磁位，用矩阵表示为

式中:n为1/2个定子齿距内的等份数;Z2为转子槽数。

将转子齿谐波绕组每个线圈所属的转子槽在不同位置下的矢量磁位两两相减，再乘以电机的铁心长度，可以得到转子齿谐波绕组每个线圈的磁通在1/2个定子齿距内的变化波形，用矩阵表示为

根据构成转子齿谐波绕组的每个线圈匝数及线圈绕向，得到转子齿谐波绕组匝数向量N(1×Z2)。当构成转子齿谐波绕组的线圈绕向为顺时针，则相应的线圈匝数为正，反之，取负值。

由式(4)和转子齿谐波绕组匝数向量N(1×Z2)计算出转子齿谐波绕组磁链在1/2个定子齿距内的变化波形为

则转子齿谐波绕组磁链在1个定子齿距内的变化波形，即一个周期内的变化波形为

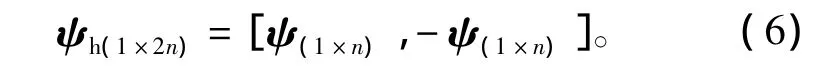
根据式(6)计算转子齿谐波绕组感应电动势波形为

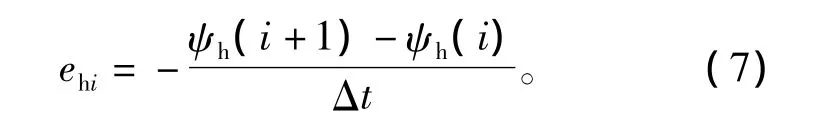
由式(7)还可以计算转子齿谐波绕组感应电动势的有效值为

式中j表示转子齿谐波绕组感应电动势波形第j个元素。

3 计算结果与实验结果比较

本文对一台齿谐波励磁的混合励磁永磁同步发电机进行了理论计算和实验。图1是该电机的截面图和原理图。定子与普通交流电机相同，转子上既有永磁体，又有励磁绕组和齿谐波绕组。电机参数:额定功率为3.25 kW，额定电压为350 V，额定电流为5.96 A，额定频率为50 Hz，极对数为3，相数为3，定子电枢绕组为Y接，并联支路数为1，每相串联匝数为180匝，转子齿谐波绕组由两条支路串联而成，总串联匝数为240匝，励磁绕组串联匝数为330匝，定子斜槽，斜1/2个定子齿距，其结构参数如表1所示。为了方便实验时能够直接测量到转子齿谐波绕组和励磁绕组中的电压以及电流，在样机的轴端安装了电刷和滑环。

为了验证本文提出的转子齿谐波绕组感应电动势波形快速计算方法的正确性，仍将1个定子齿距分成20等份，对转子相对定子在1个定子齿距内的20个不同位置进行了电磁场计算，分两种情况对电磁场计算结果进行了后处理。一是利用前10个定转子不同位置下的矢量磁位进行处理，即转子相对定子旋转1/2个定子齿距;二是利用20个定转子不同位置下的矢量磁位进行处理，即转子相对定子旋转1个定子齿距。

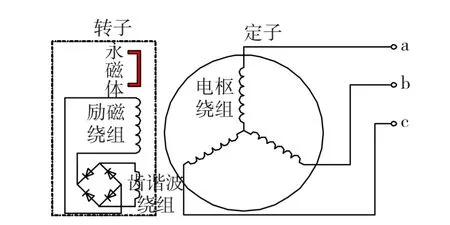
图1 齿谐波励磁的混合励磁永磁同步发电机原理图Fig.1 Schematic diagram of hybrid excitation permanent magnet synchronous generator utilizing tooth harmonic for excitation

为了能够得到转子齿谐波绕组感应电动势波形，计算和实验时将齿谐波绕组和励磁绕组开路。通过稳态电磁场计算，得到了电机空载和负载以及转子相对定子旋转1/2个和1个定子齿距时转子齿谐波绕组感应电动势有效值和波形。实测了电机空载和负载时转子齿谐波绕组感应电动势有效值和波形。图2是电机空载运行时转子相对定子旋转1/2个和1个定子齿距的转子齿谐波绕组感应电动势计算波形和实验波形。图3是功率因数cosφ=0.9(滞后)、定子电枢电流Ia=6.04 A时转子相对定子旋转1/2个和1个定子齿距的转子齿谐波绕组感应电动势计算波形和实验波形。表2是图2和图3所示的转子齿谐波绕组感应电动势波形的有效值计算结果与实验结果比较。

从图2和图3的计算波形可以看出，由于电机斜槽，且斜1/2个定子齿距，转子齿谐波绕组感应电动势波形中不存在偶数阶次的齿谐波电动势，因此，转子齿谐波绕组感应电动势波形正半周和负半周相同;根据1/2个和1个定子齿距内定转子不同位置下的电磁场计算结果处理得到的转子齿谐波绕组感应电动势的波形基本相同，从而验证了理论分析的正确性。从图2、图3和表2所示的计算结果和实验结果的比较可以看出，相同工况下的计算结果和实验结果吻合较好，为齿谐波励磁的混合励磁永磁同步发电机齿谐波励磁系统的空载和负载性能的快速计算提供了参考。

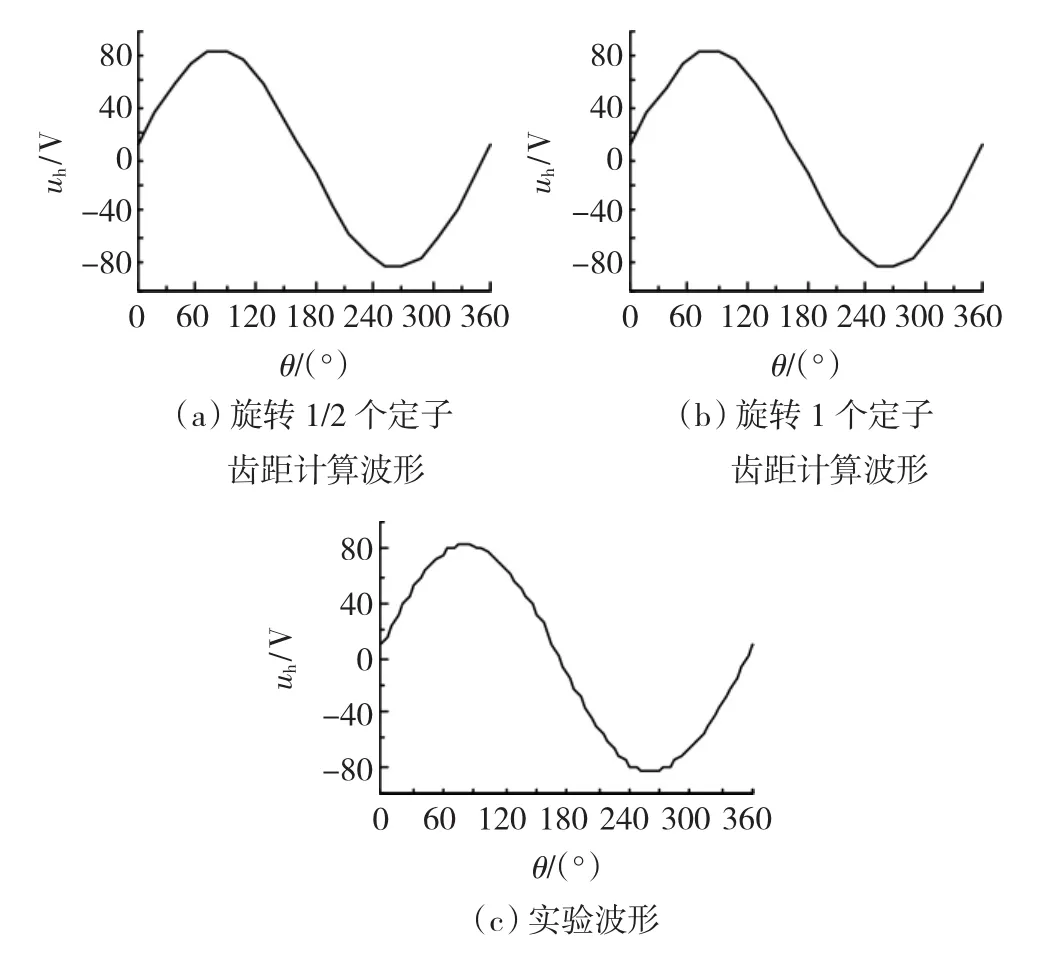
图2 电机空载运行时齿谐波绕组感应电动势波形Fig.2 Induced EMF waveform of the tooth harmonic windings under no-load operation

图3 功率因数cosφ=0.9(滞后)、定子电枢电流Ia=6.04 A时齿谐波绕组感应电动势波形Fig.3 Induced EMF waveform of the tooth harmonic windings for cosφ=0.9(lagging)and Ia=6.04 A

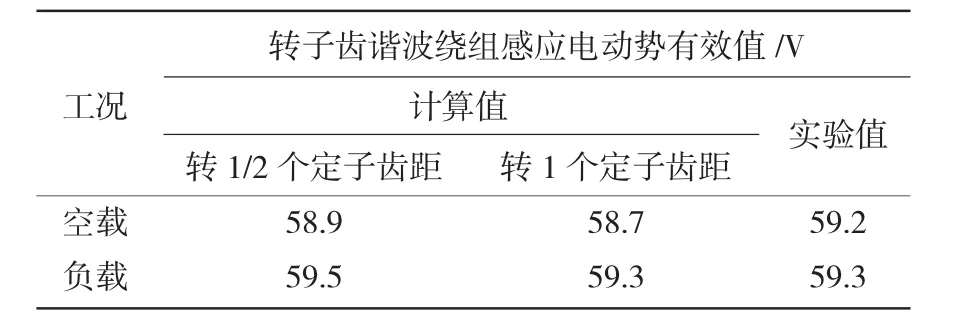
表2 图2和图3所示的齿谐波绕组感应电动势的有效值计算结果与实验结果比较Table 2 Comparison of calculated and experimental effective value of the induced EMF of the tooth harmonic windings shown in Fig.2 and Fig.3

4 结语

根据定子齿谐波磁导以及转子齿谐波绕组节距的特点，对转子齿谐波绕组感应电动势波形计算作了进一步简化，简化后的计算量为原来的1/2，即只需求解1/2个定子齿距内定转子不同位置下的稳态电磁场，就可以计算出转子齿谐波绕组感应电动势的波形和有效值。对于直槽电机，简化后的转子齿谐波绕组感应电动势计算波形存在一定的误差，而对于斜1/2个定子齿距的电机，理论上简化前后转子齿谐波绕组感应电动势计算波形相同。今后将对齿谐波励磁系统的空载和负载性能进行详细的计算与分析。

［1］YANG Chengfeng，LIN Heyun，GUO Jian，et al.Design and analysis of a novel hybrid excitation synchronous machine with asymmetrically stagger permanent magnet［J］.IEEE Transactions on Magnetics，2008，44(11):4353 －4356.

［2］张卓然，严仰光，苏凯程.切向磁钢混合励磁同步电机空载磁路计算及三维场分析［J］.中国电机工程学报，2008，28(30):84－89.ZHANG Zhuoran，YAN Yangguang，SU Kaicheng.Magnetic circuit calculation and 3-dimensional field analysis of IPM hybrid excitation synchronous machine under no-load condition［J］.Proceedings of the CSEE，2008，28(30):84－89.

［3］ZHANG Zhuoran，YAN Yangguang，YANG Shanshui，et al.Principle of operation and feature investigation of a new topology of hybrid excitation synchronous machine［J］.IEEE Transactions on Magnetics，2008，44(9):2174－2180.

［4］ZHANG Da，ZHAO Chaohui，ZHU Lei，et al.On hybrid excitation claw-pole synchronous generator with magnetic circuit series connection［C］//2008 International Conference on Electrical Machines and Systems，October 17 － 20，2008，Wuhan，China.2008:3509－3513.

［5］JABBAR M A，LIU Zhejie，DONG Jing.Time-stepping finite-element analysis for the dynamic performance of a permanent magnet synchronous motor［J］.IEEE Transactions on Magnetics，2003，39(5):2621－2623.

［6］王善铭，王祥珩，李义翔，等.交直流混合供电同步发电机空载电压波形的计算［J］.清华大学学报，2001，41(4):155 －158.WANG Shanming，WANG Xiangheng，LI Yixiang，et al.Calculation of the no-load voltage waveform of hybrid AC-DC supply generators［J］.Journal of Tsinghua University，2001，41(4):155－158.

［7］WANG Shanming，WANG Xiangheng，LI Yixiang，et al.Steadystate performance of synchronous generators with AC and DC stator connections considering saturation［J］.IEEE Transactions on Energy Conversion，2002，17(2):176－182.

［8］IDE K，TAKAHASHI M，SATO M，et al.Higher harmonics calculation of synchronous generators on the basis of magnetic field analysis considering rotor movement［J］.IEEE Transactions on Magnetics，1992，28(2):1359 －1362.

［9］KIM C E，SYKULSKI J K.Harmonic analysis of output voltage in synchronous generator using finite element method taking account of the movement［J］.IEEE Transactions on Magnetics，2002，38(2):1249－1252.

［10］黄劭刚，王善铭，夏永洪.同步发电机空载电压波形的齿磁通计算［J］.中国电机工程学报，2005，25(13):135 －138.HUANG Shaogang，WANG Shanming，XIA Yonghong.Tooth flux method of calculating no-load voltage waveform of synchronous generators［J］.Proceedings of the CSEE，2005，25(13):135－138.