一种初级永磁型直线电动机的推力特性

黄磊， 余海涛， 胡敏强， 赵晶

(东南大学伺服控制技术教育部工程研究中心，江苏 南京 210096)

0 引言

电磁推进技术是一种新兴的直线推进技术，适用于航母飞机弹射、宇航飞机助推系统和汽车碰撞实验系统等。近年来，由于电磁弹射相对于蒸汽弹射的突出优点，引起了国内外学者的研究关注［1］。电磁弹射主要采用直线电动机提供助推力，在一定距离之内将被弹射对象加速到一定的速度点以上。目前，应用于电磁弹射的直线电动机主要为直线感应电动机和直线同步电动机［2－4］。直线感应电机具有次级结构简单的优点，但是其功率因数和效率相对较低。永磁结构的直线同步电机具有高功率密度和高效率的优点，由于绕组和永磁体分别位于初级和次级，使得次级结构比较复杂，永磁体需要一定的固定装置，从而引起散热困难，增加制造成本和机械损坏。初级永磁型直线电机(primary permanent magnet linear machine，PPMLM)的出现为解决这个矛盾提供了方向，初级永磁型直线电机具有直线永磁电机的高功率密度和直线感应电机次级结构简单的双重优点。磁通切换(开关磁通)型永磁直线电机是初级永磁型电机的一种，磁通切换型永磁电机的概念最早在文献［5］中被提出。目前，对磁通切换型永磁电机的研究多为旋转电机［6－10］，对于直线型磁通切换永磁电机的研究较少，仅在文献［11－14］中报道过。本文在旋转磁通切换型电机基础上，提出一种磁通切换型永磁直线电机，并将其应用于电磁弹射。

本文采用有限元分析方法对该种电机的电磁特性进行分析。在电磁特性基础之上，对电磁弹射中的加速过程性能进行了分析研究和仿真研究。最后，通过一台试验样机来验证分析结果的正确性和合理性。

1 磁通切换型永磁直线电机结构和工作原理

应用于电磁弹射的单边磁通切换型三相永磁直线电机的基本结构如图1所示。

图1 单边磁通切换型直线电机结构图和截面图Fig.1 Structure and cross-section of PPMLM

该电机主要包括初级(动子)和次级(定子)两部分。次级固定于一定的基座之上，初级和被弹射对象相连接。次级为齿槽结构的导磁体，为消除运动时次级产生的涡流损耗，次级可采用硅钢片叠压而成。初级部分包括永磁体、绕组和铁心。初级采用模块化结构，可根据需求改变铁心个数。相邻铁心间为永磁体，临近永磁体的充磁方向为相反方向，如图1所示。每相绕组线圈绕于永磁体相邻的两个初级槽内，同相绕组串连在一起，如A1与A2、B1与B2、C1与C2串联连接。次级的齿距为电机的极距τ。为实现三相供电，相间距离为 (N±1/3)τ，次级两临近的齿距为(M±1/2)τ，其中，N为大于4的整数，M为大于1的整数。只要保持每个绕组的铁心与次级齿槽相对位置，6个绕组可随意排列。

磁通切换型永磁直线电机的工作原理可通过图2进行说明。定义A1绕组下铁心的4个齿从左到右依次为 1、2、3、4 号齿。

图2 典型位置磁场分布Fig.2 The magnetic field distribution of typical positions

图2为A1绕组的两个典型位置的磁路情况。在位置1时，磁力线主要通过A1绕组的1号齿和3号齿与次级相应齿，此时A1绕组内的永磁磁链为负向最大。在位置2时，磁力线主要通过2号齿和4号齿以及次级相应齿，绕组内的永磁磁链为正向最大。随着初级和次级位置的移动，在初级绕组内形成正负交变磁链，绕组内交变的磁场和电流共同作用形成推力，从而实现电机的直线运动。

用于分析和实验的磁通切换型永磁直线电机为小型磁通切换型直线电机。该电机的参数为:初级槽宽为10.5 mm;初级齿宽为4.5 mm;铁心叠厚为100 mm;次级齿宽为4.5 mm;次级齿距为10 mm;气隙为0.3 mm。

2 推力特性分析

为研究电机的推力特性，首先采用二维有限元方法对电机的静态特性进行研究分析。

2.1 静态特性

图3为三相绕组永磁磁链随位置变化的情况和速度为0.5 m/s时的三相空载反电动势波形。

图3 三相绕组空载波形Fig.3 The no-load flux in three phase coils

通过傅里叶变换对空载电动势进行谐波分析，谐波分量仅占基波分量的2%，所以空载磁链和反电动势可认为完全正弦波形。A相磁链和C相磁链均有恒定值的偏移量，这是由纵向边端效应引起的。感应电动势为磁链的微分，所以三相反电动势是对称的。

根据电感求解原理，采用有限元分析得出了三相饱和电感特性，图4为三相饱和自感和互感的特性曲线。

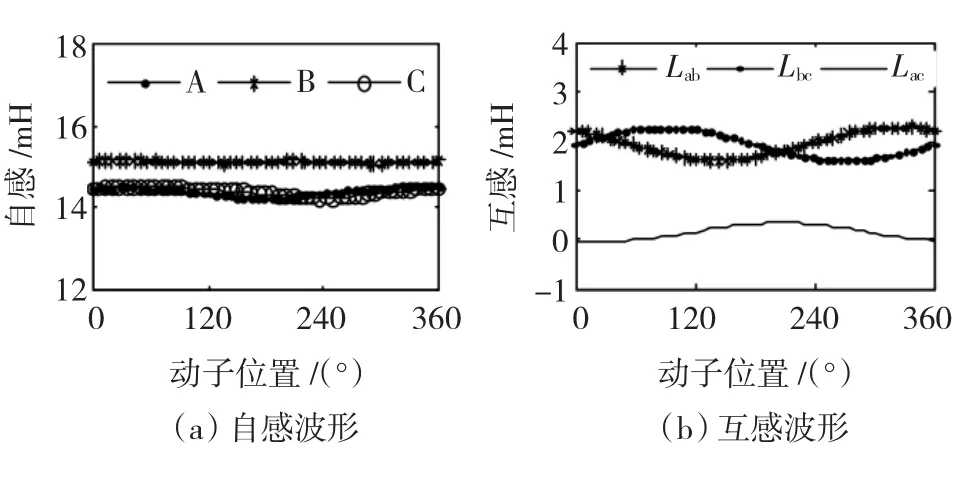
图4 静态电感特性波形Fig.4 Curves of the static inductance characteristics

2.2 推力特性分析

2.2.1 静态推力公式

根据能量法原理［15］，磁通切换型永磁电机的总的电磁推力可表示为

忽略磁链的非正弦量，采用正弦计算时，有

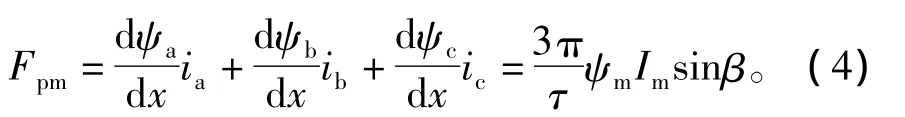
式中:τ为次级齿距;β为磁链和电流之间的夹角;ψm为一相磁链幅值;Im为一相绕组电流幅值。可见，边端效应引起的A相和C相的磁链偏移对永磁推力不产生影响。

在忽略电机纵向边端效应的情况下，磁阻推力与旋转型切换电机相类似，可得磁阻推力分量约为

式中:Ld和Lq分别为三相电感矩阵的d轴和q轴分量;id和iq分别为三相电流的d轴和q轴分量。

因为磁链的相角仅与位置相关，采用电流源供电并且保持电流滞后磁链90°，即电流与空载反电动势同相位，此时sinβ=1，电流的直轴分量id为零，永磁推力分量为最大且只与电流大小成正比，而磁阻推力约为零。此时，电磁推力为

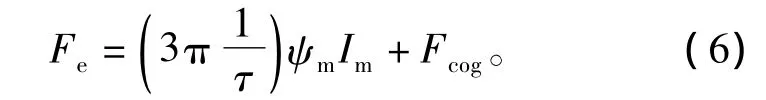
定位力是由初级和次级间的齿槽作用产生的。PPMLM的定位力平均值为零，对推力不产生任何作用，却引起电机推力波动，从而导致电机速度的波动［16］。因此，定位力越小，电机性能越稳定。通过瞬态有限元方法对该电机的定位力进行分析计算，计算结果如图5所示。

图5 定位力波形Fig.5 The cogging force of PPMLM

从图5中可以看出，该电机具有很小的定位力波动。所以，电磁推力主要为永磁推力分量。

3 电磁推力瞬态有限元仿真分析

3.1 瞬态电磁推力有限元仿真

通过场路耦合瞬态有限元分析方法对电机的瞬态推力特性进行仿真分析。忽略摩擦阻力的大小，在电流有效值为2.5 A时电磁推力随位置变化的有限元仿真结果如图6所示。

图6 推力特性曲线Fig.6 The curve of thrust force characteristic

在绕组电流有效值为2.5 A时，采用有限元方法计算的平均推力为109 N。电机的次级齿距为10 mm，通过图3可知电机磁链幅值 ψm大约为0.033 Wb，采用推力公式计算的推力为113 N。有限元计算与公式推导基本一致，证明了式(6)的正确性。

3.2 电磁弹射过程中的电磁推力有限元仿真

电磁弹射过程是在规定的运行距离内达到一定的速度，因此，保持一定的加速度是发射控制的主要目的。

由于永磁定位力是一个在零上下波动的周期变化的力，在一定周期内，平均值为零。所以，忽略定位力的影响，整个加速过程可表示为

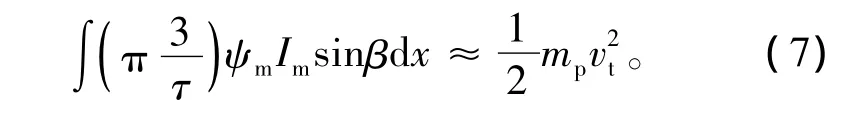
式中:mp为负载质量;vt为负载的运动速度。

由于磁链的相位只与位置相关，在保持电流滞后于磁链90°，即保持电流相位与一定位置一致时，推力分量保持最大且只与电流大小成线性正比关系。以A相空载磁链负的最大处为零位置点，三相电流随位置变化的施加方式为

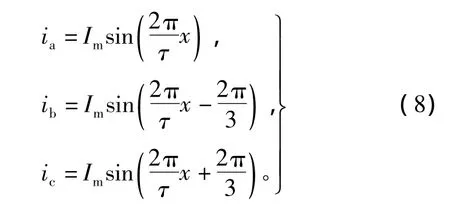
此时有

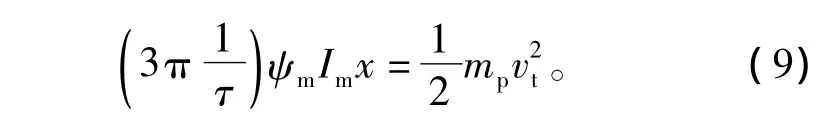
为验证发射过程，采用瞬态有限元方法对假定为10 kg的负载进行发射过程模拟。

施加电流的幅值Im为7 A，根据电磁推力式(6)计算的永磁推力分量为220 N。

图7为电磁弹射系统中磁通切换型直线电机加速过程的仿真运行曲线。

图7 弹射瞬态场仿真曲线Fig.7 Transient results during the launch

从仿真结果中可以看出，随电流的变化，电机保持一定的加速度运行，速度与电流频率变化一致，电流大小不变。整个运行过程中，电机电磁推力在205 N上下波动。有限元仿真结果表明，电机加速过程平稳，控制策略简单，证明该电机应用于电磁弹射具有很好的应用前景和优势。

4 试验研究

为了验证所提出的磁通切换型直线电机的电磁推力特性分析的正确性，首先采用与有限元计算相同参数的直线试验样机进行空载实验。图8为该试验装置结构图。

图8 试验装置结构Fig.8 The measurement system structure

当动子速度为0.5 m/s时，空载运行的一相电动势波形如图9所示。

图9 空载电压波形Fig.9 No-load voltage wave

从图9中可以看出，该电机具有正弦度很高的反电动势，且幅值和频率与有限元计算结果相一致。

其次，对电机在一定负载情况下的推力特性进行了实验研究和分析。力的平衡公式为

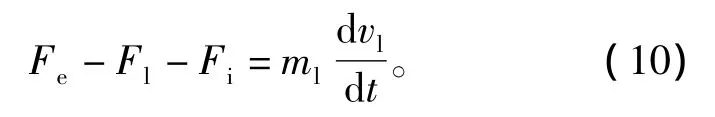
式中:Fe为电磁推力;Fl为重物重力;Fi为摩擦阻力;ml为重物质量;vl为重物运动速度。在实验中，保持电机运行于匀速状态，电磁推力等于重物重力与摩擦阻力之和。重物为100 N，电机从0.12 m/s的速度调整为两倍速度，电流的变化情况如图10所示。

图10 速度变化下电流波形Fig.10 The current wave at different speeds

由特性曲线可知，速度的大小取决于电流频率。在速度变化时，电流大小基本保持不变。采用分析的电流控制方法时，电磁推力只取决于电流大小。此时，电流有效值大约为2.9 A，略大于同负载下的有限元计算值和公式计算值，这主要是由于摩擦阻力的作用。

为验证推力计算公式，同样保持电机运行于匀速状态，对不同重物负载下的电流进行测量。图11为不同负载下的电流有效值的变化情况，图11给出了公式计算值、有限元计算值和试验测量值。

从图11中可以看出，3种结果基本一致。随电流增大后，有限元和测量结果略微下降，这主要是由电机初级铁心内磁路饱和引起的。而电机测量值在空载时仍有电流，这是由摩擦阻力引起的。测量值表明，推力大小与电流成正比，且3种结果的斜率大小基本接近，验证了推力公式与有限元结果的正确性，从而验证了所提出的电机特性。证明了id=0控制策略下的电流与推力的线性关系，从侧面验证了电磁弹射过程的正确性。

图11 不同负载的电流值Fig.11 The current with different loads

5 结论

本文在旋转磁通切换型直线电机的基础之上，提出一种应用于电磁弹射的磁通切换型初级永磁直线电机，在对其静态特性分析的基础之上，推导了推力公式，并采用有限元方法验证了推力特性。探讨其应用于电磁弹射过程中的特性。采用样机验证了电机的电磁特性。计算和试验结果表明该电机具有以下的优点:

1)PPMLM的永磁体和绕组均位于初级，减少了永磁数量，降低了整体成本。PPMLM的次级结构简单，次级仅为导磁材料的齿槽结构。

2)PPMLM具有较小的定位力，降低了推力的波动，提高了电磁推力性能。

3)相对于其他直线电机复杂的控制策略，PPMLM应用于电磁弹射，采用简单的控制策略即可实现推力和加速度的直接控制，简化了控制策略，降低了控制成本。

以上优点表明，该种直线电机应用于电磁弹射系统中，具有很好的应用前景。本文的研究内容和结论为该类型电机在电磁弹射系统中更深入的研究奠定了基础。

［1］JAYAWANT B V，EDWARDS J D，WICKRAMARATNE L S，et al.Electromagnetic launch assistance for space vehicles［J］.IET Science，Measurement and Technology，2008，2(1):42 －52.

［2］HALL David，KAPINSKI James，KREFTA Mark，et al.Transient electromechanical modeling for short secondary linear induction machines［J］.IEEE Transaction on Energy Conversion，2008，23(3):789－795.

［3］MIRZAEI Mehran，ABDOLLAHI Seyed Ehsan.Design optimization of reluctance synchronous linear machines for electromagnetic aircraft launch system［J］.IEEE Transactions on Magnetics，2009，45(1):389 －395.

［4］KOU Baoquan，HUANG Xuzhen，WU Hongxing，et al.Thrust and thermal characteristics of electromagnetic launcher based on permanent magnet linear synchronous motors［J］.IEEE Transactions on Magnetics，2009，45(1):358 －362.

［5］RAUCH S E，JOHNSON L J.Design principle of flux-switch alternator［J］.Transactions of The American Institute of Electrical engineers.Part III:Power apparatus and systems，1955，74(3):1261－1268.

［6］ZHU Z Q，CHEN J T，PANG Y，et al.Analysis of a novel multitooth flux-switching PM brushless AC machine for high torque direct-drive applications［J］.IEEE Transactions on Magnetics，2008，44(11):4313－4316.

［7］花为，程明，ZHU Z Q，等.新型磁通切换型双凸极永磁电机的静态特性研究［J］.中国电机工程学报，2006，26(13):129－134.HUA Wei，CHENG Ming，ZHU Z Q，et al.Study on static characteristics of novel flux-switching doubly-salient PM machine［J］.Proceedings of the CSEE，2006，26(13):129 －134.

［8］黄志文，沈建新，方宗喜，等.用于弱磁扩速运行的三相6/5极永磁开关磁链电机的分析与优化设计［J］.中国电机工程学报，2008，28(30):61 －66.HUANG Zhiwen，SHEN Jianxin，FANG Zongxi，et al.Analysis and optimal design of a 3-phase 6/5-pole PM flux-switching motor for flux-weakening application［J］.Proceedings of the CSEE，2008，28(30):61－66.

［9］贾红云，程明，花为，等.磁通切换永磁电机等效模型与控制策略分析［J］.电机与控制学报，2009，13(5):631 －637.JIA Hongyun，CHENG Ming，HUA Wei，et al.Equivalent model and control strategies analysis for flux-switching permanent-magnet motor［J］.Electric machines and control，2009，13(5):631－637.

［10］林明耀，张磊，李鑫.轴向磁场磁通切换永磁电机齿槽转矩分析［J］.电机与控制学报，2009，13(6):787 －791.LIN mingyao，ZHANG lei，LI xin.Analysis on cogging torque in axial field flux-switching permanent magnet machine［J］.Electric machines and control，2009，13(6):787 －791.

［11］WANG C F，SHEN J X，WANG L L，et al.A novel permanent magnet flux-switching linear motor［C］//4th IET International Conference on Power Electronics，Machines and Drives，PEMD 2008，April 2 －4，2008，York，UK，2008:116－119.

［12］ZHU Z Q，CHEN X，CHEN J T，et al.Novel linear flux switching permanent magnet machines［C］//11th International Conference on Electrical Machines and Systems，ICEMS 2008，October 17 －20，2008，Wuhan，China.2008:2948 －2953.

［13］WANG Canfei，SHEN Jianxin，WANG yu，et al.A new method for reduction of detent force in permanent magnet flux-switching linear motors［J］.IEEE Transactions on Magnetics，2009，45(6):2843－2846.

［14］JIN Mengjia，WANG Canfei，SHEN Jianxin，et al.A modular permanent magnet flux－switching linear machine with fault tolerant capability［J］.IEEE Transactions on Magnetics，2009，45(8):3179－3186.

［15］汤蕴璆.电机内的电磁场［M］.北京:科学出版社，1998:341－367.

［16］ZHU Z Q，THOMAS A S，CHEN J T.Cogging torque in fluxswitching permanent magnet machines［J］.IEEE Transactions on Magnetics，2009，45(10):4708－4711.