GM(1,1)模型改进算法及其应用研究
2011-06-05李宏坤,赵长生,郭骋,赵利华
李 宏 坤, 赵 长 生, 郭 骋, 赵 利 华
(1.大连理工大学 机械工程学院,辽宁 大连 116024;2.大连理工大学 工业装备结构分析国家重点实验室,辽宁 大连 116024)
0 引 言
所谓预测就是将历史数据进行数学建模,借助数学模型进行外推,将模型的外推值作为真实值的参考的过程.而机械设备寿命预测是指根据历史监测结果进行分析,估计设备故障可能发生的时间,以便主动掌握设备运行状况.设备寿命预测对于减少设备维修成本和提高生产效益具有重要实际意义.
目前,机械设备寿命预测方法主要包括损伤积累法和特征参数法.影响机械设备寿命的因素不但较多而且变化复杂,且损伤积累预测方法的分散性较大[1],所以损伤积累预测方法在机械设备寿命预测中难以实现.特征参数预测方法是寿命预测的研究方向之一,其关键是特征提取和参数的建模方法.特征参数预测方法较多,如灰色理论预测、模糊预测、神经网络预测、混沌预测、回归预测、时间序列预测等.可以说,没有一种方法能够预测所有序列,每一种预测方法都有各自的适用范围和局限性[2].
GM(1,1)模型是灰色预测理论中最具有代表性的基础内容,具有贫信息、高精度、简机理等建模特点,已在机械设备寿命预测[3、4]等各个方面得到广泛应用并取得了不错的效果[5、6].但是传统GM(1,1)预测模型也并非完美,其最大不足就是预测偏差大,适用范围窄.为了提高此方法在机械设备预知维修中的实用性,本文对GM(1,1)的预测模型进行改进算法研究.
1 GM(1,1)模型建模机理
设满足建模条件的原始序列为X(0)={x(0)(1),x(0)(2),…,x(0)(n)},则 1-AGO(一 次累加生成)序列为


求解方程(2)并将其解在离散情况下描述:

观察式(3)可知,只有解出C、a和u方可得到序列的预测值.

将式(2)在区间 [k,k+1]积分得

取背景值

则式(5)可以表示为
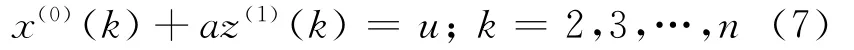

其中

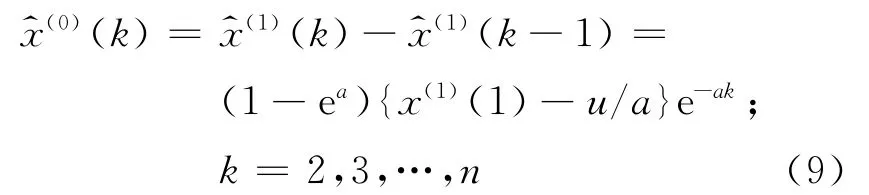
通过分析发现,传统GM(1,1)模型推导过程存在三点不足.一是未对原始序列做预处理.分析式(9),GM(1,1)模型序列具有指数发展规律,故原始序列的发展趋势对GM(1,1)模型的拟合及预测精度具有一定的影响.二是背景值的求解方法有待进一步完善.事实上,原始序列间隔越小、1-AGO变化越平缓,误差就会越小.当原始序列速度增长较快时,则会产生较大的滞后误差.三是初始值选取不合理也是传统GM(1,1)建模过程产生误差的根源之一[7],并且没有考虑参数x(1)(1)对参数a、u的影响.通过分析式(6)发现,如何确定x(1)(1)的值也会影响后续的预测精度.
2 一种新的GM(1,1)模型的提出
对于不满足要求的原始序列,采取加权预处理.经研究,改善原始序列光滑度和构造更为合理的背景值均可减少滞后误差,对于背景值构造过程中的误差改进,许多文献已给出卓有成效的改进方法[8~10],考虑到根式变换方法简单易行,并且其逆变换具有还原误差的独立性,本文选择根式变换方法减少滞后误差带来的影响.对于初始值^x(1)(1)的选择,本文在文献[7、11]的基础上,充分考虑x(1)(1)对参数C、a、u的影响,给出一种基于最小平均相对误差的GM(1,1)改进算法,新的求解方法如下.

将式(10)代入式(9)得
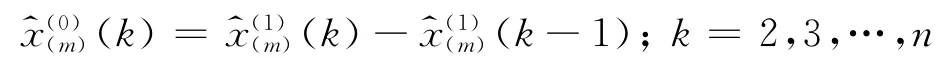
假定
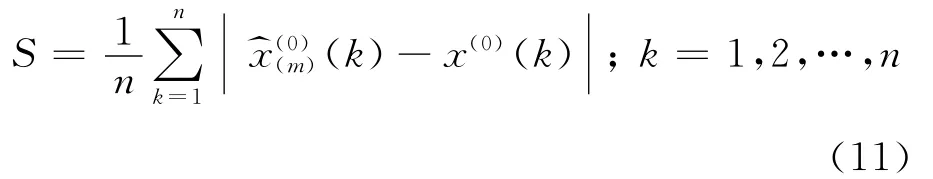
求出令S达到极小值的参数m,进行式(4)~(9)步骤.综上,改进GM(1,1)预测模型步骤如下:
(1)原始序列预处理;
(2)1-AGO获得生成列;
(3)对生成列做根式变换;
(5)还原并检验.
3 实例分析
3.1 指数型增长序列
取指数型增长序列为X(0)= {1.34986,1.82212,2.45960,3.32012,4.48169},由于数据为指数型增长数据,直接进行步骤(2)~(5).改进算法与文献[7、8]方法对比结果见表1.
分析表1,改进算法(Ⅱ)的结果是最好的.可以验证,对于指数型增长数据,随着根式节次的增大,改进算法的误差将会进一步减小.
3.2 一般型增长序列
为便于说明,原始序列取文献[12]中1972~1982年全国电视机产量数据.经分析,原始序列为一般增长规律的序列,且最后一个数据不符合整体增长趋势.但对于预测来说,新信息是最有价值的,本文将1979~1981年的产量数据分别乘以权重2/3做加权预处理.传统GM(1,1)建模方法的平均误差高达263.17%,改进算法、文献[8]和文献[12]方法结果见表2.

表1 指数型增长序列Tab.1 Exponential increasing series
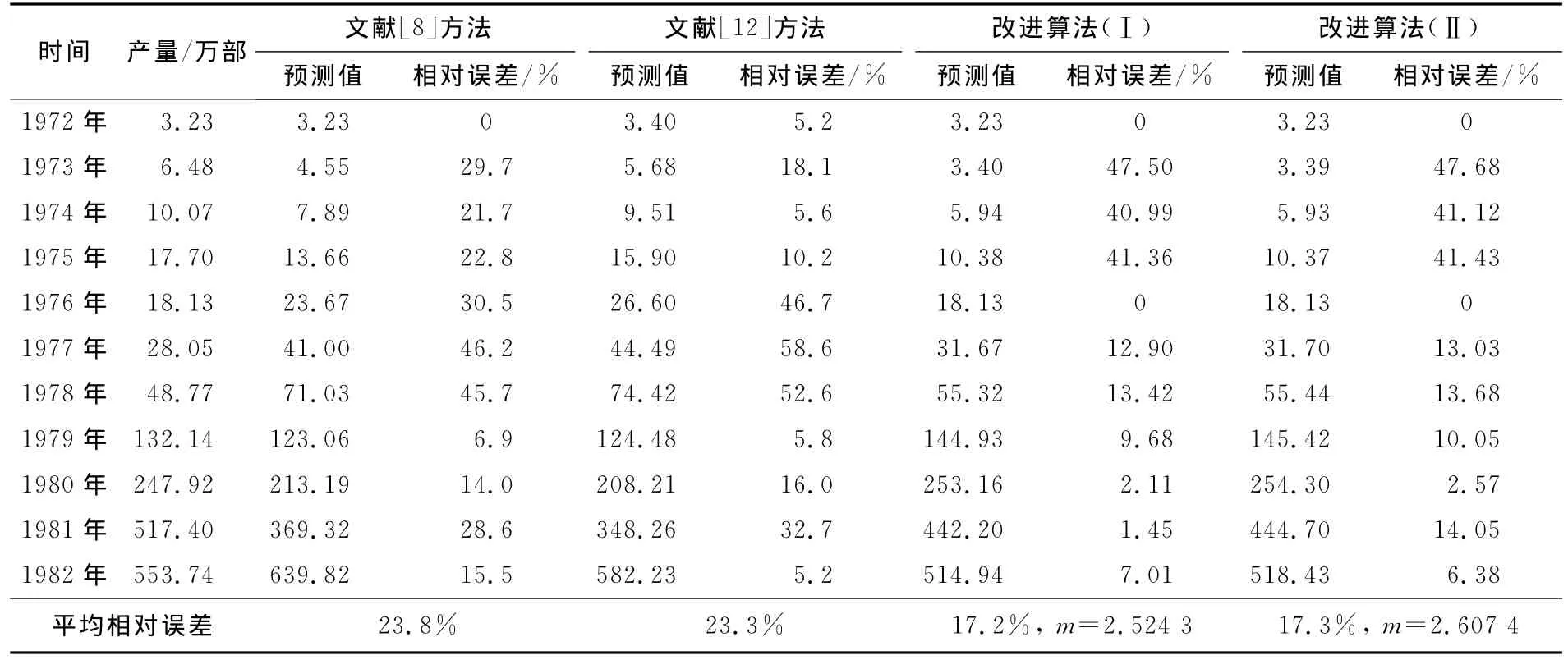
表2 一般型增长序列Tab.2 General increasing series
与普通序列相比,改进算法(Ⅱ)对于指数规律较强的序列尤为有效,对于非指数规律序列,可以在实际应用中择优建模.不管使用哪种方法,其精度都要远高于传统模型.同时,改进算法的最后几个数据和实际的数据拟合程度较高,对后续的预测具有较高的指导意义,因为对于预测来说,最有价值的信息就是新数据.改进算法(Ⅰ)的预测效果见图1.
3.3 机械设备寿命预测
数据来自某工厂磨床设备轴承座1995-01-05至1995-07-05连续7个月的振动加速度测试,仪器选用大连理工大学振动工程研究所PDM2000数据采集仪,采样频率为1280 Hz,采样时间为4 s,1~6月份的测量结果见图2.
提取加速度的均方根值作为特征参数,原序列X(0)= {10.02,10.76,10.87,13.28,14.89,17.55,19.80}.根据文献[5],均方根值符合灰色预测数据内涵特点,可以将其作为灰色预测序列.将前6个月数据建模,7月份数据作为对比.基于最小二乘法的二次、三次函数拟合的平均相对误差分别为1.944%和2.009%,改进算法(Ⅰ)(2月份数据除以权重系数C=1.06,m=3.391)的相对平均误差为1.717%,显然改进算法的预测效果是较理想的.7月份的预测值为20.23 mm/s2,预测相对误差为2.184%,经灰色检验,关联度符合要求,预测精度级别为很好.预测效果见图3.若设备的报警值为19 mm/s2,则根据预测规律计算该设备报警的时间为6月21日.

图1 1972~1982年全国电视机产量改进算法(Ⅰ)预测Fig.1 Prediction of improved algorithm (Ⅰ)for nationwide TV quantity in 1972-1982

图2 1~6月份加速度幅值Fig.2 Amplitude of acceleration from January to June

图3 机械设备寿命预测Fig.3 Mechanical equipment life prediction
4 结 语
通过分析传统GM(1,1)模型推导过程,指出原始序列规律、1-AGO序列光滑度及其初始值是影响传统GM(1,1)模型预测精度的主要因素.本文在已有改善序列光滑度方法的基础上,指出了对原始数据做加权预处理的必要性;在确定最佳初始值时,综合考虑初值对预测参数C、a、u的影响,给出了一种基于加权和最小平均相对误差的改进算法.该改进算法不但可以较大幅度地提高拟合及预测精度,而且扩展了传统GM(1,1)模型的适用范围.为验证改进算法的有效性,将改进算法用于机械设备的预知维修中,取得了不错的效果,促进了设备故障预知维修的发展.新信息对于预测是最有价值的,当获得新的测量数据时,利用GM(1,1)新陈代谢模型可以进一步提高预测精度.改进算法对于指数规律的序列很有效,对于不满足要求的原始序列数据需尝试不同权重,如何给不满足要求的原始序列数据分配最佳权重有待进一步研究.
[1]刘蓉生.机械装备的剩余寿命预测[J].机械,1993,20(6):38-43
[2]王 亮,刘 豹.单变量时间序列预测:综述与评价[J].天津大学学报,1991(2):70-76
[3]施国洪.灰色预测法在设备状态趋势预报中的应用[J].中国安全科学学报,2000,10(5):49-53
[4]王旭亮,聂宏伟.基于灰色系统GM(1,1)模型的疲劳寿命预测方法[J].南京航空航天大学学报,2008,40(6):845-848
[5]邓聚龙.灰预测与决策[M].武汉:华中科技大学出版社,2002
[6]肖新平,宋中民,李 峰.灰技术基础及其应用[M].北京:科学出版社,2005
[7]张大海,江世芳,史开泉.灰色预测公式的理论缺陷以及改进[J].系统工程理论与实践,2002,22(8):140-142
[8]于德江.灰色系统建模方法的探讨[J].系统工程,1991,9(5):9-12
[9]陈 洁,许长新.灰色预测模型的改进[J].辽宁师范大学学报(自然科学版),2005,23(3):110-114
[10]谭冠军.GM(1,1)模型的背景值构造方法和应用(Ⅰ)[J].系统工程理论与实践,2000,20(4):98-103
[11]张 辉,胡适耕.GM(1,1)模型的精确解法[J].系统工程理论方法应用,2001,10(1):72-74
[12]李云贵,李清富,赵国藩.灰色GM(1,1)预测模型的改进[J].系统工程,1992,10(6):27-31
