水下核爆作用下混凝土重力坝模型破坏试验

陆 路， 李 昕， 周 晶

（大连理工大学 水利工程学院，辽宁 大连 116024）

0 引 言

目前各国学者就水下爆炸作用下水中结构的响应开展了大量的实验研究.如Rajendran对4 mm厚的300mm×250mm的矩形板及直径290 mm的圆柱壳（长1m）作了系列水下爆炸荷载作用下的响应试验，测得不同爆炸距离下高强度合金钢（HSLA）的应变分布情况[1]；Ramajeyathilagam对长×宽×厚为0.55m×0.45m×0.004m的长方体高强度低合金钢进行了水下爆炸荷载作用下的响应试验，得到了矩形板在不同炸药量及不同作用距离下的非线性瞬态动力响应，试验结果同数值研究结果十分吻合[2]；Houlston等对不同强度的方形薄板进行了水下爆炸试验研究，获得响应的位移分布值[3、4].张效慈等对钢质圆柱壳（直径0.5m，长1m，壁厚5mm）进行了1kg TNT不同作用距离下的水下爆炸动态响应试验研究，获得了不同部位的应变分布值[5]；李国华等对浮动平台进行了水下爆炸冲击谱的测量与分析[6].进行实船水下爆炸试验研究十分昂贵，目前比较少见.意大利在退役的“EXMARGOTTIN1”号驱逐舰上进行了全尺度的6次不同强度的水下爆炸试验，获得了全船及加筋板在水下爆炸荷载作用下动态响应分布[7]；高秋新对一2 500t级驱逐舰进行了实船水下爆炸试验，获得舰船受振荡效应下的振型和频率[8]；中国船舶科学研究中心将某驱逐舰缩比成一弹性船模，进行了水下爆炸荷载作用下的动态响应试验[9]；张绮蓉等对某舰船进行了水下非接触爆炸试验，获得了水下爆炸对舰船总纵强度与局部强度的影响[10].终上所述可以看到，水下爆炸对水中结构响应的试验研究主要集中于金属材料及舰船.

水利枢纽工程的关键建筑——大坝的安全，直接关系到下游的工农业生产和人民的生命安全.文献[11]数模了水库中小剂量药包爆炸时混凝土重力坝的弹性响应，但人们更关心的是水库中核爆对大坝破坏程度的估计.由于还不能建立混凝土在强冲击作用下破坏机制精确的计算模型，目前还难以对这一过程进行数值仿真模拟.本文试用机械冲击模拟大坝在强冲击波作用下的破坏过程，开展大坝在核爆作用下的破坏试验.

1 模型试验方法

1.1 原型重力坝及试验方法

本文模型试验对象为一混凝土重力坝，高150m，上游坡直立，下游坡度1∶0.75，如图1所示.假设有一个W＝106t TNT当量的核弹在坝体上游R＝637m处的水库中爆炸，即采用TNT爆炸来模拟核爆炸，但实际上模拟原型坝体存在困难，如TNT的密度按1.6t/m3计，那么106t TNT当量的核弹相当于一直径d≈106m的球形TNT药包，假设水库的深度h为150m，则h/d≈1.50，这不可能形成深水爆炸的效果.

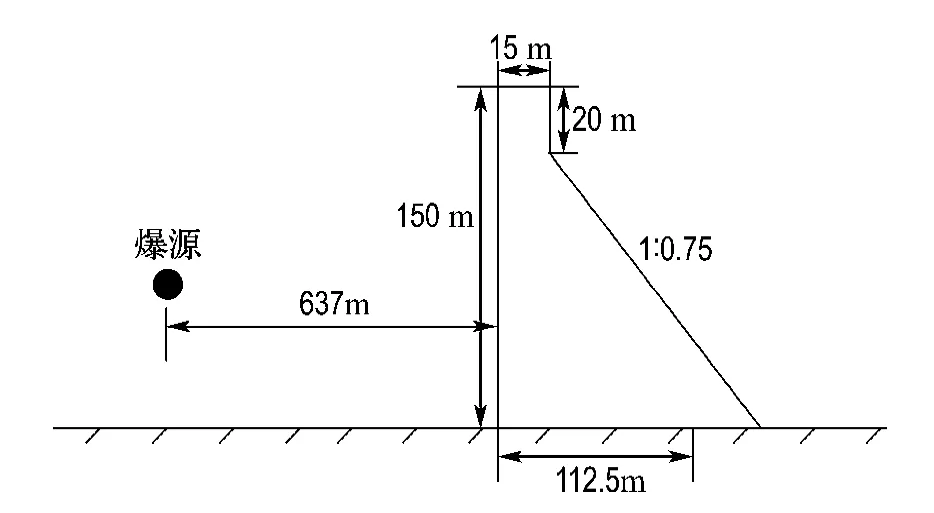
图1 原型重力坝Fig.1 Prototype of gravity dam

假定水库中核爆对大坝的破坏作用主要源自一次冲击波，核爆时水面水底现象及二次波动对大坝的破坏作用可以忽略，那么可以采用简单的机械冲击来模拟一次冲击波.在19世纪70年代，霍布金生曾经用落体方法使钢丝突然受拉伸来测量钢丝的强度.本文则用落体方法来形成作用在坝体上的冲击波，如规定的原型大坝，取一次冲击波的最大压强pm＝73.245MPa，历时曲线示于图2.显然，对于极短历时的强冲击过程，对大坝的破坏作用取决于总冲量I的大小，而压强p的历时影响不大.

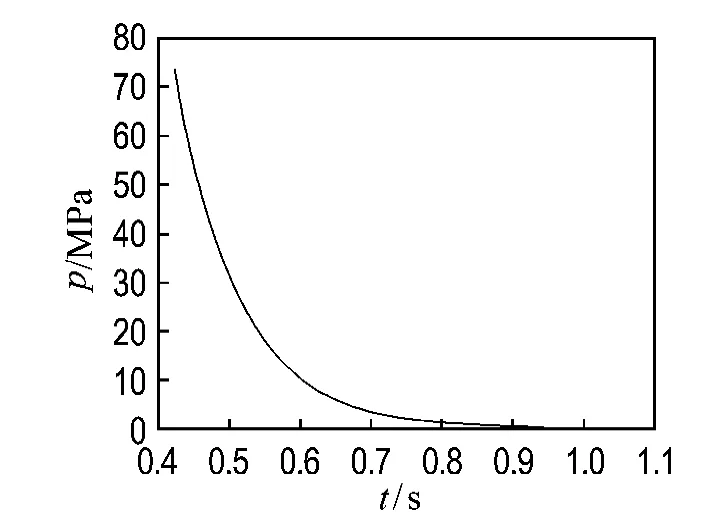
图2 W＝106 t，R＝637m时水中冲击波压强与时间关系Fig.2 Relation between underwater shock wave pressure and time for W ＝106 t，R＝637m

设作用在原型大坝上游面面积Ap上的总冲量为Ip，那么按相似关系可以确定作用在相应模型坝上游面面积Am上的总冲量

式中：λI为冲量比尺.根据Im选定冲击体的悬挂高度和质量.

1.2 试验设计

1.2.1 相似关系 试验遵循弹性－重力相似律.

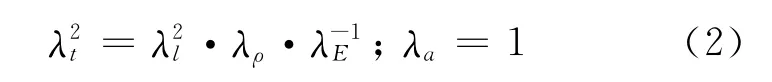
式中：λt为时间比尺；λl为几何比尺；λρ为密度比尺；λE为弹性模量比尺；λa为加速度比尺.

本试验的特点是以原型冲量Ip作为模型设计的控制量.因

式中：F为作用力；t为时间，所以I的相应比尺

式中：λF为外力比尺.因进行满库试验时，有λρ＝1，所以

因此模型中的Im由下式确定：

Ip为已知值，λl根据具体条件选定.

因为试验中用质量为Mm的悬锤形成冲量，所以若悬锤悬挂位置与冲击点位置的高差为Hom，那么悬锤到达坝面时的冲量

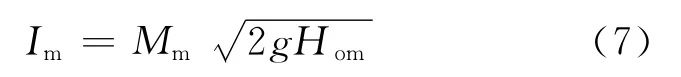
由式（7）可知对给定的Im可以有Mm和Hom的不同组合，可根据条件选择.

1.2.2 模型材料 模型材料是指模拟重力坝的修建材料——混凝土的材料.本试验模型采用材料为由水泥、粉煤灰、矿石粉、重晶石粉和水按一定比例配制而成的仿真混凝土.在浇注模型坝的同时，浇注立方体试块，用SANS型10t压力机进行材料的抗压试验.2组冲击试验的模型材料主要力学指标列于表1.

表1 模型坝材料的主要力学指标Tab.1 Basic mechanical properties of model dam material

本试验取几何比尺λl＝200，若原型混凝土的抗压强度和抗拉强度分别按40×106Pa和4×106Pa，密度2 400kg/m3，那么要求模型坝的抗压、抗拉强度和密度分别为0.2×106、0.02×106Pa和2 400kg/m3.表1中的这3个指标虽然和要求值有一定差异，但差别还不是很大.虽然模型

材料的弹性模量比要求值低很多，但对强冲击破坏试验起控制作用的应是强度，弹性模量的差异不至于引起显著的影响.

1.3 试验装置

由于核爆产生的冲击波强度高，冲击波在水中传播速度快，在一定范围内球面波可以作为平面波来考虑，坝体上游面受到的核爆冲击荷载可以认为沿坝高和坝轴线方向均是均匀分布的，同时考虑到坝体横向分缝形成坝段，各个坝段独立工作，所以取一个坝段研究可以代表整个坝体.

试验装置的后视图和侧视图分别示于图3（a）和3（b）.模型坝高0.75m；模型坝宽度取值约为0.15m，相当于原型的坝段宽30m（几何比尺为200）.其他尺寸均示于图3.采用5个悬锤，悬吊高度均为0.6m，悬锤是铅制成的立方体，其尺寸为0.15m×0.15m×0.086 0m.5个悬锤作用坝面时保证全坝高同一时刻均受到冲击荷载.悬锤的质量Mm由下式确定：

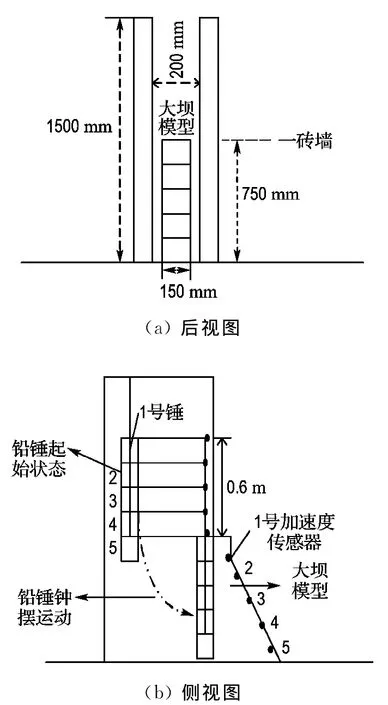
图3 试验装置示意图Fig.3 Sketch of test rig setup

浇注模型坝时分成两种情况：一是直接在光滑底板上浇筑，二是在有锚钉的底板上浇筑.在邻近坝下游面埋设了AR－5F型号加速度传感器，它的位置示于图3（b）.冲击前的第一种模型示于图4.

图4 冲击前的第一种模型Fig.4 Type one model before impact

2 试验结果

2.1 第一种模型的试验结果

各坝块反应特征列于表2.冲击后的坝体破坏状态示于图5，冲击后加速度传感器复零良好，5个加速度传感器的历时曲线分别示于图6（a）～（e）.

表2 坝体对冲击反应的主要动力特征Tab.2 Dynamic characteristics of dam response under impact

图5 第一种模型冲击后的坝体破坏模式Fig.5 Failure mode of type one model dam after impact

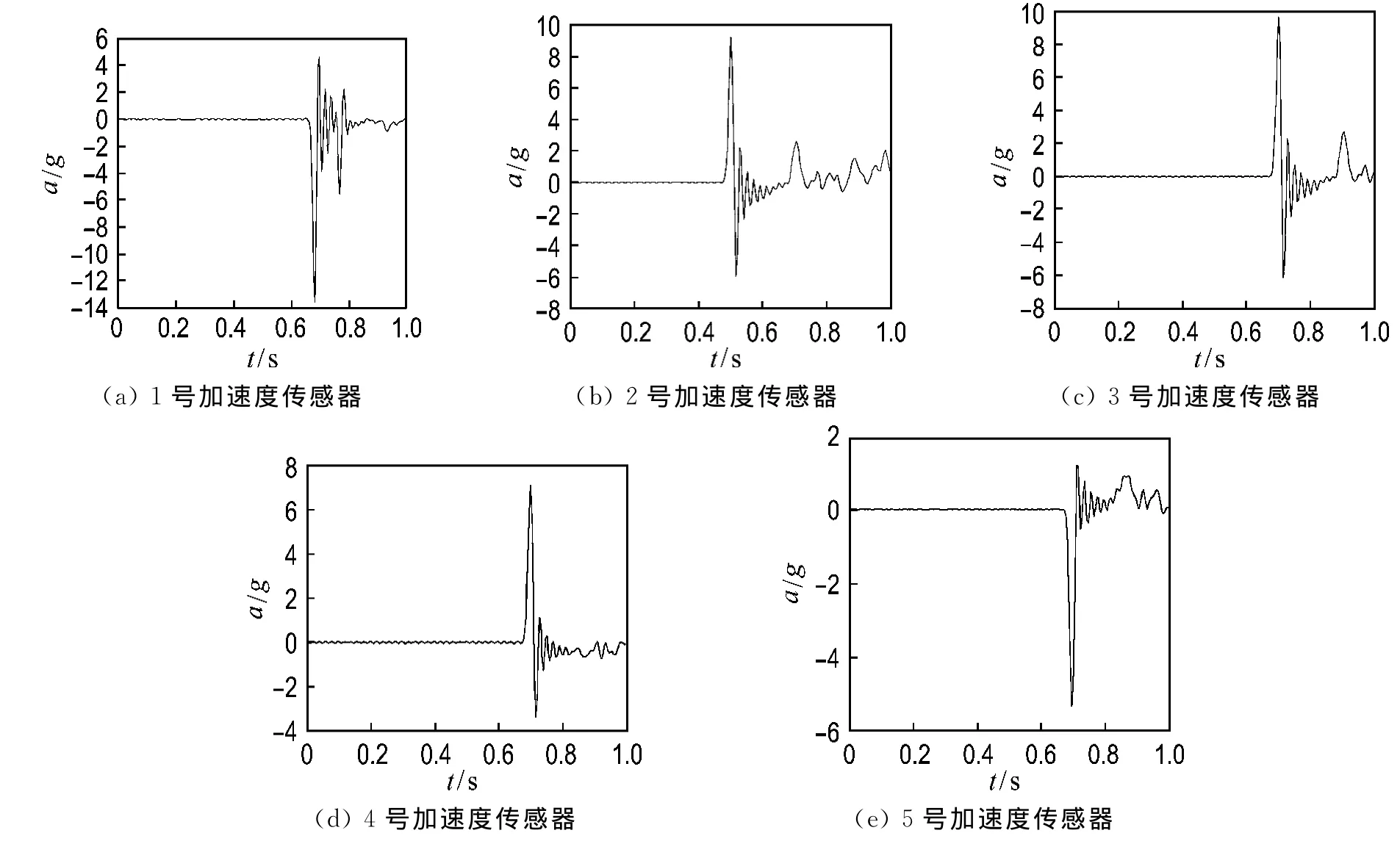
图6 冲击后第一种模型加速度传感器响应的历时曲线Fig.6 Acceleration sensor response time history curves of type one model dam after impact

2.2 第二种模型的试验结果

在相同的冲击下，第二种模型的1号与5号加速度传感器的记录示于图7（a）与7（b），冲击后的破坏坝体示于图8，各坝块反应特征也列于表2.

3 试验结果分析

3.1 破坏模式

强冲击作用下坝体内的应力分布比较复杂，所以坝体的失效模式也有多种.有的是因裂缝扩展而形成的贯穿性断裂，如图5中的基底裂缝和上部的水平裂缝；有的是因冲击应力过大，冲击时间过短，裂纹来不及扩展而引起的局部碎裂，如图5中上游面和图8中的碎块.所以总体而言，强冲击下是断裂、碎裂、层裂[12]、滑移和抛掷的组合破坏模式.

图7 冲击后第二种模型加速度传感器响应的历时曲线Fig.7 Acceleration sensor response time history curves of type two model dam after impact

图8 第二种模型冲击后的坝体破坏模式Fig.8 Failure mode of type two model dam after impact

比较图5和8发现，两个模型坝的破坏特征有较明显的区别.图5中的坝底贯穿性剪断，坝的第5块（最下一块）在模型中滑动0.13m，如按变形相似比尺（等于几何比尺）换算，原型中滑动26 m；第3、4、5号坝块内无贯穿性裂缝，保持良好的整体性；在2号坝块以下的下游面，仍基本保持光滑状态，无痂片痕迹.图8中的模型，由于坝底锚固，坝底虽碎裂，但不能确切判断是贯穿性剪断.第5号坝块基本上无整体滑移；距坝底0.28m以上的坝块都已破碎，被抛掷；坝的整个下游面都已成碎块散落.出现如上差异的原因有二：坝体的固结方式；坝体材料强度的差异.图5中的坝体受冲击后坝底很快被剪断，坝体滑移，因此冲击荷载部分释放，减小了坝体中的冲击应力，再加上坝体强度较图8中的坝体强度大，所以破碎程度较轻.但对原型而言，无论形成图5还是图8中的破坏，计及库水的作用都会形成毁灭性的灾害.

3.2 冲击弹性模量与冲击阻尼

受应变速率的影响，混凝土的动弹性模量大于静弹性模量，但常用的动弹性模量也都是在应力不大、应变速率不高的条件下测定的，布里奇门（1931年）曾指出：“固体的体积压缩模量K在高压时升高.”K与弹性模量E之间存在线性关系，所以可推断强冲击下混凝土的动弹性模量将高于通常所应用的动弹性模量.

图6是第一种模型上的5个传感器的加速度历时曲线，应力波到达时加速度急剧升高，应力波通过后则为坝的衰减自振.5个加速度传感器曲线基本一致.相应的振动频率列于表2，平均频率约为41.5Hz.用ANSYS有限元程序进行试算后，得与ρ＝2 900kg/m3、f0＝41.5Hz相应的模型坝的冲击弹性模量（EI）m＝2.38×108Pa，远大于表1中用静力测定的弹性模量（E0）m＝4.95×106Pa.（EI）m还略大于要求值1×108Pa，但原型的弹性模量2×1010Pa不是在冲击条件下确定的.

3.3 冲击应力

因为只在靠近坝的下游面埋设了加速度传感器，所以只能估计传感器处的冲击应力.令坝体中的位移为d，模型中的冲击接近平面问题，则d沿X向（坝体横向）的传播过程近似为（沿坝高向为常数）

式中：x为离上游坝面的距离；C0为坝体的纵波波速；f为任意函数.把式（8）分别对x和t求导，则有

式中：f′表示对函数f求导.由式（9）、（10）可得

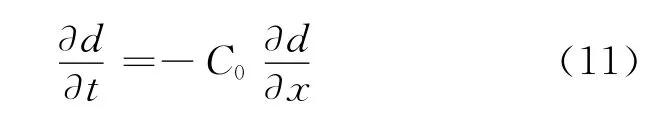
而

所以有

式中：v是坝体中质点运动的速度，其中C0＝

根据图6，可近似令加速度

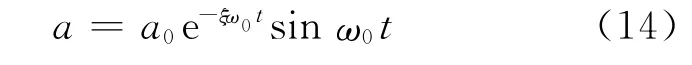
由式（13）可得

显然

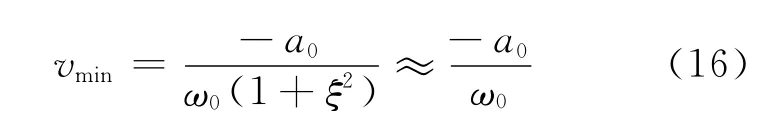
因此

各个坝块的C0、ω0是相同的，但各坝块的a0不一样.如1号坝块a0＝14g，则（σx）max＝0.44×106Pa；3号坝块的a0＝10g，则（σx）max＝0.31×106Pa.由于1号坝块已碎裂，3号坝块外观仍完整，由此可以近似判断图5模型坝的实际抗压强度为0.3×106Pa＜fc＜0.5×106Pa，远大于表1中的抗压强度，这正如文洛克等（1933年）早就指出的“随着变形速度的增大断裂应力也增大；如果变形速度足够大，那么材料不产生预先的屈服就开始破坏.”

3.4 能量平衡

以第一种模型为例，分析本试验系统能量的输入与输出.能量输入：进行过无坝时的摆下落试验，摆越过最低点后的回复高程基本和初始高程一致，所以可以忽略摆的摩擦损失，且假定摆与坝面撞击后速度立即为零，因此系统的输入能量为

当Hom＝0.6m，Ei＝448.35J.

坝体的耗散能量包括坝体滑移能量、断裂能、头部抛掷所需能量、振动阻尼耗能、碎裂能及其他耗能，具体计算如下：

（1）坝体滑移能量

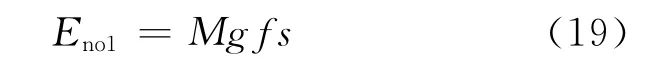
式中：M为坝体质量，本试验M＝99.62kg；f为坝体底面与坝基的摩擦因数，取0.8；s为坝体移动距离，本试验s＝0.13m.则得到Eno1＝101.53 J.

（2）水平裂缝的断裂能

式中：A为断裂面积；Gf为单位裂缝面积所吸收的能量.Gf较难确定，根据线弹性断裂力学理论，Gf与KⅠc、E之间有如下关系：

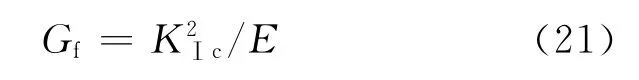
文献[13]建议

式中：fc为10cm×10cm×10cm混凝土试件的立方体强度，KIc为断裂韧度.

如用表1中的fc和E及式（21）、（20），得出的Gf1≈800N/m，远大于文献[14]中常规混凝土的试验结果Gf＝110～150N/m（相应的fc＝23.8 MPa）.若采用本文冲击试验的估计值则Gf会减小，Gf2≈43N/m，当取Gf1＝800N/m，那么Eno2＝0.122m2×800N/m＝97.6J；若取Gf2≈43N/m，则Eno2＝0.122m2×43N/m＝5.25J.

（3）头部的抛掷能量

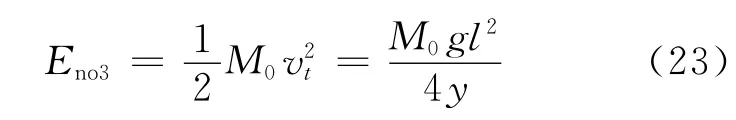
式中：M0为抛掷部分的质量；l为抛掷距离；y为抛掷体原始位置离地面的高度.取M＝5kg，l＝40.0J.

（4）坝体的振动阻尼损耗（按1周计）

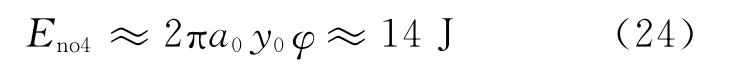
式中：a0为加速度峰值，φ为阻尼比，y0为振幅.

（5）坝体的破碎能

突加应力很大时应力会引起坝体碎裂.坝在刚受到冲击后，外观完整的混凝土1d后会破碎成小碎块，此种形式消耗的能量即为破碎能.曾纳（1952）描述过一个例子：“穿甲弹垂直射入并穿透装甲板后不立即发生破坏，但是在穿过后几分钟至几天的时间内，穿甲弹的头部却发生碎裂”.破碎能可用下式估计[15]：

式中：ξ为小于1的一个系数.图8的模型整体位移基本为零，即Eno1≈0，所以Eno5比较大，碎裂程度高于图5中的模型.

（6）其他耗能

把混凝土坝受到强冲击后产生的热能等耗能归结在一起用Eno6表示：

4 结 论

（1）采用机械冲击模拟水下核爆，基于弹性和重力联合相似准则，开展混凝土重力坝的破坏试验是可行的.

（2）坝体与坝基的接触程度决定了大坝在冲击荷载作用下的破坏模式.当坝体与坝基弱连接时，冲击荷载作用下坝体发生较大的整体位移，坝体上部破碎；当坝体与坝基锚固连接时，冲击荷载作用下坝体无明显的整体位移，但坝体上部破碎范围明显扩大.

（3）通过模型试验发现，在高强度冲击荷载作用下坝体的强度、弹性模量和阻尼比均远大于静力试验或地震等动力试验所得到的结果，需要进一步开展材料试验研究.

[1] RAJENDRAN R.Linear elastic shock response of plane plates subjected to underwater explosion [J].International Journal of Impact Engineering，2001，25：493－506

[2] RAMAJEYATHILAGAM K.Non－linear transient dynamic response of rectangular plates under shock loading [J]. International Journal of Impact Engineering，2000，24：999－1015

[3] HOULSTON R，SHATEN J E.Structural response of panels subjected to shock loading [C]//55th Shock and Vibration.Doyton：US Naval Research Lab，1985

[4] HOULSTON R.Damage assessment of naval steel panels subjected to tree－field and enhanced air－blast loading [C]// Advances in Marine Structures－2.Essex：Elsevier Science Publishers Ltd.，1991

[5] 张效慈，李玉节，赵本立.深水爆炸水动压力场对潜体结构的动态影响[J].中国造船，1997，38（4）：61－68

[6] 李国华，李玉节，张效慈.浮动冲击平台水下爆炸冲击谱测量与分析[J].船舶力学，2000，4（2）：50－60

[7] 彭兴宁.船舶结构对水下非接触爆炸的响应[J].舰船力学情报，1994（3）：26－33

[8] 高秋新.爆炸引起的船体振荡[J].舰船力学情报，1992（9）：41－47

[9] 李珙华.×××舰弹性船模的三维水弹性理论分析及试验结果比较[R]//中国船舶科学研究中心科技报告.武汉：中国船舶科学研究中心，1994

[10] 航空航天部六零三研究所.GJB 2329—95 舰船抗核加固总要求[S].北京：国防工业技术委员会，1995

[11] 徐俊祥，刘西拉.水中爆炸冲击下混凝土坝动力响应的全耦合分析[J].上海交通大学学报，2008，42（6）：1001－1004

[12] 张 磊，胡时胜，陈德兴，等.混凝土材料的层裂特性[J].爆炸与冲击，2008，28（3）：193－199

[13] 于晓中，居 襄.混凝土的强度和破坏[J].水利学报，1983（2）：22－35

[14] 于晓中，张玉美，郭桂兰，等.混凝土断裂能GF[J].水利学报，1987（7）：30－37

[15] 朱 锡，侯海量，谷美邦，等.抵御小口径火炮弹道侵彻装甲防护模拟实验研究[J].爆炸与冲击，2006，26（3），263－268