深水浮式海洋平台水动力性能计算研究

王言英

（大连理工大学 船舶工程学院，辽宁 大连 116024）

0 引 言

深水浮式海洋平台为深海油气勘探开发的重要装备.目前，面临着我国南海海域油气资源勘探开发实际情况，亟待解决深水半潜式钻井平台自行设计与建造的大量关键技术，其中平台在深海海洋环境中的诸多水动力性能问题，为其设计、建造与营运中的关键技术之一.

近年来，结合深水半潜式钻井平台项目，完成了相关课题研究，建立了可以用于工程设计的算法并改进了一些以往的算法.对于海洋环境条件的确定，重点讨论了更大重现周期设计波的参数[1、2].平台在波浪中的运动及其遭遇的波浪荷载计算，解决了经典的高阶边界元法计算单元边界上速度势导数不连续而影响计算精度的问题，实现了在时域求解非线性问题的方法[3～6].平台在波浪中遭遇砰击荷载的计算，给出了局部压力系数的直接计算方法[7、8].建立了平台气隙的计算方法，完成了对Veslefrikk半潜式平台设计气隙的计算校验[8～10].立管动力响应的计算重点考虑了非线性对涡激振动的影响和减缓涡激叶片的优化设计问题[11～14].对于系泊定位系统建立了三维锚链线的动力模型，而动力定位系统主要考虑的是推力器的合理布置和吊舱螺旋桨的应用[15～23].建立了基于笛卡儿剪切单元网格的改进的自由表面捕捉方法，并用于求解出入水问题，实现了诸如砰击和构件海上起落出入水的工程应用计算[24～26].本文运用自行开发的软件平台，计算深水浮式海洋平台设计中水动力性能参数.

1 海洋环境参数确定

海洋环境参数通常委托海洋环境研究相关单位提供，包括海域地理位置，周边与海底地貌、水深、风、浪、流，以及空气与海水物理参数等.根据用户要求需要提供两类环境资料：一是平台工作海域的营运环境资料；另一是平台工作期间可能遭遇的最恶劣环境资料.

有关船级社对平台设计的极端海况已有相应的规定，如挪威船级社（DNV）规定为设计波高32 m的海况；美国船级社（ABS）则规定为设计风速100kn的海况.实际上根据Beaufort风级表给出的最大风速与相应的最大波高关系[1]，100kn风速对应的最大波高约32m，即为百年一遇的极端海况.

飓风卡特里娜袭击墨西哥湾（2006年7月）后，人们对于百年一遇设计波高的标准感到疑惑，出现是否应当考虑海洋平台设计规范修订的问题.实际上，这是应用更长的重现周期对应的海况从事海洋结构物设计的问题.将重现周期外推到500a，可以看出极端海况的有义波高同重现周期100a的相比，从32m增加到34m，约有2m的增幅[2].

2 运动与波浪荷载计算

格林函数法被广泛地用于船舶和海洋结构物在波浪中遭遇的荷载与运动计算.考虑三维浮体在规则线性波作用下6个自由度的运动，通过求解满足物面、自由表面、底部和辐射条件的Laplace方程，以确定浮体的运动和波浪诱导荷载.相应于各自由度的速度势函数，可以用满足自由表面与底部边界条件的Haskind源与格林函数的积在淹湿物面的积分得到[3].格林函数必须满足含奇点的Laplace条件和相应的自由表面、底部与辐射条件[4].当格林函数确定后，可以利用满足物面条件的第二类Fredholm方程，求出物面上的源强分布，进一步确定各自由度的速度势与总势，以及浮体的运动附加质量与阻尼系数[5]，最后应用线性化的Bernoulli方程求得波浪扰动力.

以经典的高阶边界元方法计算单元边界上速度势，因其导数并不连续而影响计算精度.应用基于B－样条的边界元方法，能够保证速度势和速度势导数在边界上的连续性.NURBS（非均匀有理B样条）能够精确表达二次曲面，基于NURBS的边界元方法又能同CAD方便集成[6].NURBS曲面的形式不仅可以表达物体的几何形状，也可以用来表达物体表面上的速度势.把速度势函数表达成二维参数空间上的NURBS曲面形式[6]：

式中：φi，j为速度势的控制点；wi，j是控制点 的权值；i＝ 0，1，…，m；j＝ 0，1，…，n；Ni，k（u） 和Nj，l（v）分别为k和l次B样条基函数.在边界元方法计算中，使用NURBS形式对表面的速度势进行离散，对表面速度势函数φ的求解就转换成了对速度势控制点φi，j的求解.

通常基于NURBS的边界元方法中速度势使用式（1）表达，需要预先设定速度势控制点的权值wi，j.第一种方法是权值wi，j全部为1，即不使用有理形式表达速度势φ.面元上的几何形状仍然保持使用NURBS的表达形式，而速度势的表达基于普通的非均匀B样条形式.另一种解决方法是使用加权余量法，通过使积分方程的残差最小来建立方程组.对离散的积分方程使用Galerkin方法，使残差直接在参数空间对应的NURBS样条函数上达到最小，可以得到可计算的线性方程组.

图1是船舶迎浪运动时的波浪弯矩和剪力响应函数，同试验值和STF法计算结果相比较表明，基于B－样条的边界元方法的计算结果比较准确[6]，可以满足工程应用的要求.

图1 S－175迎浪中剖面垂向波浪弯矩和剪力响应函数Fig.1 RAO of vertical bending moment and shear force on the mid－ship profile for S－175in head wave

3 冲击与砰击荷载预报

底部砰击是指船舶航行或海洋结构物遭受恶劣海况时，由于剧烈的纵摇与升沉运动，使其底部露出波面，在底部重新进入波浪的瞬时，同波浪产生猛烈的瞬时的非线性冲击现象.目前从事砰击荷载预报的主要有规范法、试验法和理论计算法.

考虑环境因素的作用，将船体运动和砰击理论计算相结合，利用工程软件为冲击荷载提供了直接计算方法[7].对砰击荷载进行预报，首先要判断底部砰击发生的条件.通常底部产生砰击要同时满足船体底部出水和产生可计量的压力两个条件.因此，底部砰击发生的充分条件是当船体底部出水回落撞击水面时，船体横截面与波浪之间的垂向相对速度超过某一临界速度，用数学表达式表示如下：

式中：H为波高；分别为横剖面与波浪的垂向相对位移和速度为临界速度，其中L为船体长度，g为重力加速度.采用三维频域GREEN函数法程序计算船舶运动[5、6]，利用频时转换在时域中预测各种海况下砰击发生的频率和横剖面与波面的垂向相对位移与速度[8].其后由计算出砰击压力p[7]，式中ρ为海水密度，k即所谓的局部压力系数，至今大都依赖于经验数据或模型试验数据库提供.

实际上，可以应用二维的CFD出入水软件平台求解剖面局部压力系数.应用FLUENT软件，根据船体底部所关注点相对于波面的最大速度，计算得到不同时刻和位置上的压力系数，从而可以给出船体各横剖面上在无因次时间域中的最大压力系数，即所谓局部压力系数k＝max（CP）（见图2）.进一步分析整理可以得出局部压力系数关于船体横剖面形状的函数，经过必要的试验或经验资料的验证作为工程设计的依据.

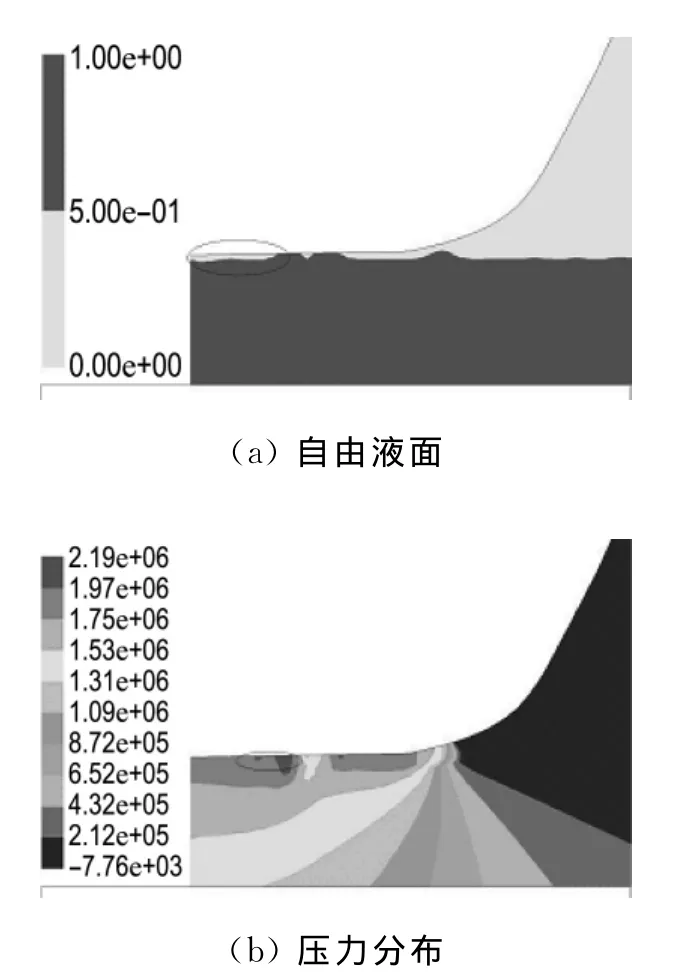
图2 18站＝－0.01时刻的自由液面和压力分布Fig.2 The shape of the free surface and pressure distribution at＝－0.01for the 18th Station

由一浮式生产储油船（FPSO）的算例，发现平底半宽是影响船形剖面入水砰击压力系数的重要参数.无因次化平底半宽变量表示为＝b/B，其中b为平底半宽，B为设计吃水1/10处水线半宽.计算得到的不同剖面的和相应的砰击系数k的关系如图3所示.

图3 k同横剖面参数的关系曲线Fig.3 The relative curve between k and geometric parameter of cross section

4 气隙校验

气隙是指波峰表面与平台下甲板间的距离，极限波浪条件下保持正的气隙是设计的基本要求.现用a0表示静水气隙值，η（t）表示波表面瞬时升高，δ（t）表示平台的垂向位移.如果η与δ相等，则气隙响应仍然等于静水气隙a0.大多数情况下气隙响应可以用a（t）＝a0－r（t）表示，其中表示平台与波浪相对位移的r（t）＝η（t）－δ（t）.当气隙值a（t）＜0，即相对位移r（t）大于静水气隙a0时，可能会产生甲板砰击及上浪.

规则波中垂向相对位移的幅值响应函数可以通过下式求解：

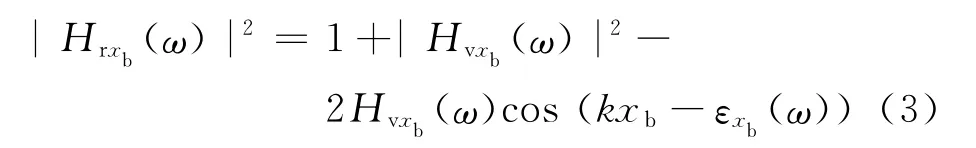
式中：｜Hrxb（ω）｜为平台xb剖面下表面与波浪表面垂向相对位移的幅值响应函数；｜Hvxb（ω）｜为平台xb剖面垂向位移速度的幅值响应函数；εxb（ω）为平台xb剖面垂向位移的相位响应函数.｜Hvxb（ω）｜与εxb（ω）分别可以通过以下两式进行计算：

其中Hz（ω）、Hθ（ω）、εz（ω）和εθ（ω）分别为平台在规则波中的垂荡和纵摇运动幅值和相位的频率响应函数.采用平稳线性系统，对于给定的波浪谱可以计算得到气隙响应的谱函数.

文献[10]对Veslefrikk半潜式平台的设计气隙进行了计算校验[9].该平台的作业海况的有义波高Hs＝14m，采用JONSWAP谱波谱函数，谱峰周期Tp＝13s，γ＝3.0.

图4为平台中心点垂向运动的谱函数，进一步计算得到表1的统计特征参数.

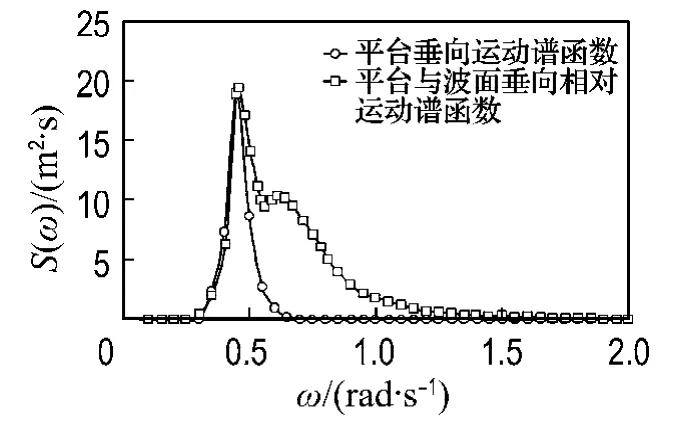
图4 垂向运动谱函数Fig.4 Vertical motion spectral function

表1 平台中心点相对波面垂向运动的谱函数统计特征Tab.1 Statistical characteristics of vertical motion spectrum for the central point of platform relative to wave surface

该平台的静水气隙值（hd）为17.50m；谱分析给出3h海况下平台与波浪相对位移的极值（h1/N）为17.65m；根据试验观测数据计算在N＝909时，经过计算可知3h海况下平台与波浪相对位移的极值为17.49m，三者的偏差在2%以内.因此可以认为Veslefrikk平台设计给出的静水气隙具有一定的合理性及可靠性.

5 立管动力响应分析

隔水管是海洋浮式生产系统中的重要附属设备，其内部有高压的油或气流通过，外部则承受风、波浪、海流的作用，另外加上所连浮体的漂移的影响，隔水管处于极其复杂的海洋环境中.同时，由于漩涡的释放会引起隔水管的纵向、横向振动，甚至会使漩涡脱落频率锁定在结构的振荡频率上，使结构产生更大的振荡幅度，从而造成工程结构的失效或损坏.因此如何准确地预报出实际海况中隔水管的动力响应和涡激振动问题，对于逐渐向深海发展的海洋开采事业具有重大的意义.

为了探讨在波浪海流共同作用下隔水管的动力响应及涡激振动，根据三维空间中隔水管运动的微分控制方程，以Matteoluca改进的Vanderpol尾流振子模型为基础，计算涡激振动时隔水管与流体之间的相互作用.通过Hermite插值函数对隔水管的运动微分方程进行有限元离散，基于非线性分析理论，利用更新的拉氏描述（ULA）建立了考虑几何非线性、预应力、涡激流固耦合等复杂因素影响的综合非线性增量平衡方程，并采用Newton－Raphson迭代法和Newmark方法相结合的方法建立了空间隔水管非线性涡激动力响应的增量迭代算法.最后给出了考虑几何非线性与外界荷载作用简化的位移分布包络线，以及横向涡激振动响应曲线.计算结果表明，所采用的方法正确、有效，可以为隔水管的生产设计及理论分析提供依据[12].图5、6分别给出考虑和不考虑几何非线性和流体力非线性对各个方向立管位移包络线形状的影响，其中Lb为距海底的距离.

通常隔水管动力响应计算是将波浪传播方向和海流速度方向视为同向进行分析，或者仅考虑稳定海流产生的涡激振动.进一步基于三维空间进行动力响应和涡激振动分析，且波浪传播方向和海流速度、方向是任意的.隔水管可视为小尺度构件，波浪和海流对它的作用力用Morison方程计算.通常的做法是将Morison方程中的水动力系数假设为常数，并将该方程的非线性项进行近似线性化.改进的算法是将Morison方程中的系数依据外界环境条件确定，并且保留了方程的非线性项，在计算中采用迭代求解，使之计算的结果更符合实际情况[13].

图5 不考虑和考虑几何非线性隔水管横向位移Fig.5 Displacements in xand ydirection considering and without considering geometrical nonlinearity

通过von Mises应力计算得到隔水管关键点处的应力时间历程，再根据雨流计数法、S－N曲线和Miner线性累积损伤模型估算隔水管的疲劳寿命，并采用 Wirching方法进行了可靠性分析.最后给出了运用以上方法得到的隔水管的疲劳可靠性分析结果.

当前在立管表面加装螺旋涡片成为有效的消涡装置，应用CFD软件FLUENT计算立管绕流流场及其沿流向阻力和沿横向升力变化，以实现对加装螺旋涡片几何形状与尺度以及数量的优化是有效可行的方法[13].计算表明加装螺旋涡片抑制立管的涡激振动是有效的，采用螺距比为5，片宽为0.15D，数量为3的螺旋涡片装置，可能取得较好的抑制涡激振动的效果.图7（a）、（b）分别给出在Re＝800条件下，绕一固定光体立管和带有3组螺旋涡片固定光体立管的瞬时涡线和总压分布.不论从释放涡的形态，还是从后方的压力分布，都可以清晰地看出释放涡被抑制的效果.在实际流态雷诺数下的数值模拟，或者关于计算雷诺数下计算结果的尺度效应，尚待进一步的研究来揭示.

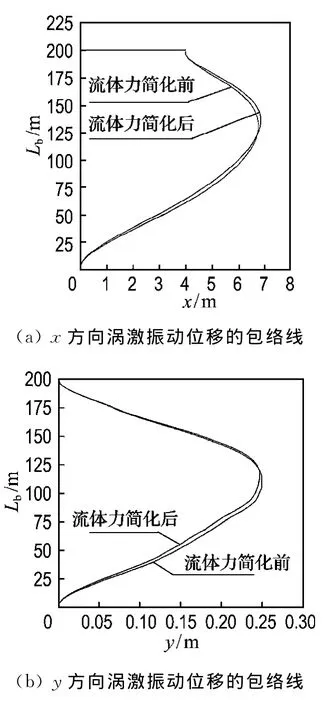
图6 流体力简化前后隔水管横向位移Fig.6 Displacements in x and y direction under different hydrodynamics

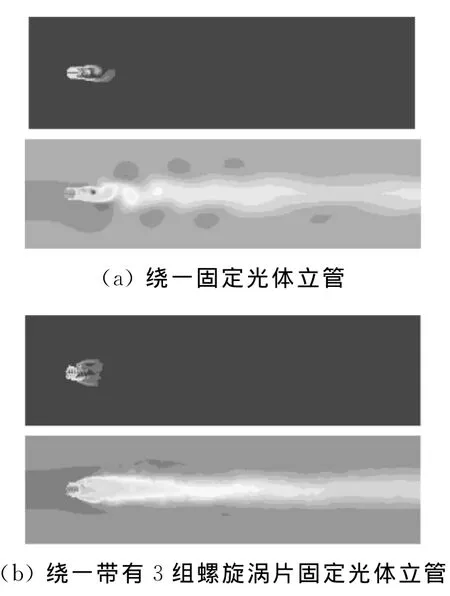
图7 在Re＝800条件下绕一固定光体立管和带有3组螺旋涡片固定光体立管的瞬时涡线和总压分布Fig.7 Instantaneous vorticity contours and total pressure contours for the flow past a fixed bare riser and a fixed riser with three helical strakes at Re＝800

6 系泊与动力定位评价

深水海洋平台通常备有锚链系泊系统和动力定位系统，分别用于不同作业水深与海洋环境条件.

对于锚链系泊系统需要通过计算确定在各种平台作业状态下和不同海洋环境条件下，满足定位条件的锚链张力，或者在允许的锚链张力条件下平台的定位指标.在频域内采用对浮体运动方程与锚泊线运动方程耦合求解的方法，计算得到半潜式海洋平台在限制工作水深的运动位移与锚泊线上的张力[14～16].在时域中则将在频域内对浮体运动方程求解的计算结果转换为时域结果，同锚链线运动的时域方程耦合求解锚泊浮体在限制工作水深的运动位移与锚链线上的张力[17～19].

为了提高常规锚链线方程的计算精度，采用一种考虑锚链线上各种受力的三维锚链线模型来计算锚链的位移与受力.根据牛顿第二定律，得出三维锚链线的动力模型，见式（6）.其中ε为锚链线单位长度应变；Fh为锚链线在该点的次法线（b）方向上锚链受到的流体力；Fn为锚链线在该点的法线方向上锚链受到的流体力；G为锚链线在该点的切线（t）方向上锚链受到的流体力；α为锚链线沿长度方向上的倾角；θ为锚链线与船体轴线的夹角；T为锚链线上的张力；U、V、W为局部坐标系下的锚链线速度分量；Wc为在水中单位长度锚链线的重量；m为单位长度锚链线的质量.方程（6）有6个未知量U、V、W、α、θ、T和2个参变量t、s，而方程的个数也为6个，所以方程组是封闭的.

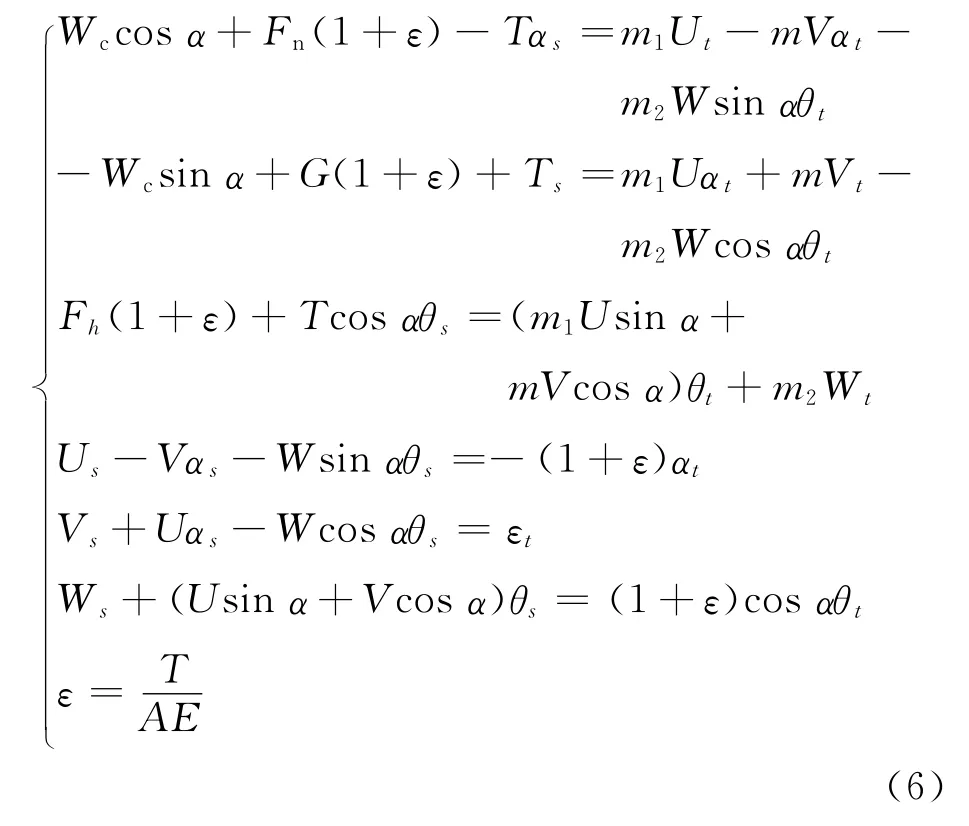
图8所示为一FPSO系泊系统中第7号锚链张力时间历程的计算值同试验值的比较[18]，可以看出数值模拟结果具有工程应用的精度.

图8 FPSO第7号锚链张力时间历程计算与试验值比较Fig.8 Comparison of computational and experimental results for tension forces on mooring line No.7 of a FPSO

深水系泊导致新的系泊线和锚的出现，诸如合成锚缆的应用，不仅是系泊线材料的改变，更重要的是其构成全然不同[19]；吸力沉箱的应用，不仅是锚的形式的改变，更重要的是导致了系泊系统及其计算方法的改变[19].绷紧索系泊系统克服了传统悬链式系泊系统在深海中应用的困难，由于纤维系缆回复刚度大，平台水平偏离量大大减小；同等水深下使用绷紧索系泊系统，需要较短的纤维材料系缆，能节约成本，尤其在深水和超深水条件下的经济性非常明显；具有更小的系泊半径，系泊基础占用的海床面积小，减小了同附近其他水下设施相碰撞的危险[20].

目前大多数深海钻井和采油平台都采用动力定位系统作为深水作业状态的定位装置，根据平台设置海域的环境条件和平台的运动特性，选用螺旋桨推进器系统，提供各个方向上的水平力和艏摇弯矩，形成一个时变的推力系统来抵消外在的时变的环境荷载.多数半潜式钻井平台采用8个推进器，该推进器系统形成了一个冗余系统，存在无数多个不同的推力和方向的组合，均满足特定的水平力和艏摇弯矩.实际应用中推力的分配方法是重要的，文献[21]以最小化推进系统的能耗为目标函数，同时还考虑推进器的推力极限、最大推力变化速率、最大旋转速率、推进器推力的禁区、奇异结构等因素，应用序列二次规划法建立了一种合理高效地解决动力定位系统推力分配问题的方法.

作为动力定位系统的推力器，吊舱式螺旋桨为当前广泛应用的形式之一.对于选配的推力器从事水动力性能计算，以检验其系统的定位效能是必须的.计算方法有基于模型系列试验的图谱法，利用常规螺旋桨敞水性能图谱修正得到相应的吊舱式螺旋桨性能[22、23]；也有基于面元法的吊舱式螺旋桨敞水性能的直接计算的软件平台.

7 出入水问题的解及其工程应用

海洋平台在现场组装或在作业过程中，经常会有大型构件入水和出水作业.物体在以某种速度出入水过程中，当其同水表面接触时会产生较高的水动力压力，从而会导致物体运动轨迹的改变，甚至于会导致物体遭到破坏的荷载.

应用自由表面捕捉法处理水表面问题.该方法以有限体积法求解带自由表面的非均匀的不可压缩流体的Euler方程，其自由表面同绕流物体是非连续性接触的.计算域的外边界上的密度、速度与压力为常数，允许流体以当地的速度大小和方向自由进出；物体边界上速度遵守不可穿透条件，密度保持零法向梯度，运动为单自由度的（对于二维问题，向上或向下运动），只存在垂向压力梯度.笛卡儿剪切单元格用作离散网格系统，其中包括固体单元、流体单元与剪切单元三种不同类型的单元网格.须考虑物体同流体的相互作用，物体与流体全耦合的方法用以计算物体运动速度与位移[24～26].

文献[24]给出如下算例.一长10m、直径0.2 m的水密的圆柱，水平地置于距初始静止水面上方0.4m处.圆柱的质量为1 570.8kg，起重吊缆的刚度为2 000kN/m.不计吊缆的阻尼和质量，其等速移动速度为1.0m/s，起重机及其母船位置固定，荷载向下为正.图9为圆柱入水时的垂向速度和荷载的水动力压力随时间的变化，可以看出荷载的速度呈周期性震荡，从而会导致负载的水动力震荡.震荡频率为34.656Hz，接近于吊缆的自振频率图10所示为荷载吊缆张力变化的时间历程.可以发现荷载入水前的吊缆张力为15 393.84N，即近似于圆柱的重力；入水过程中其张力高频震荡；而当负载完全没水后张力在12 320.62N上下变化，接近圆柱的浮力.

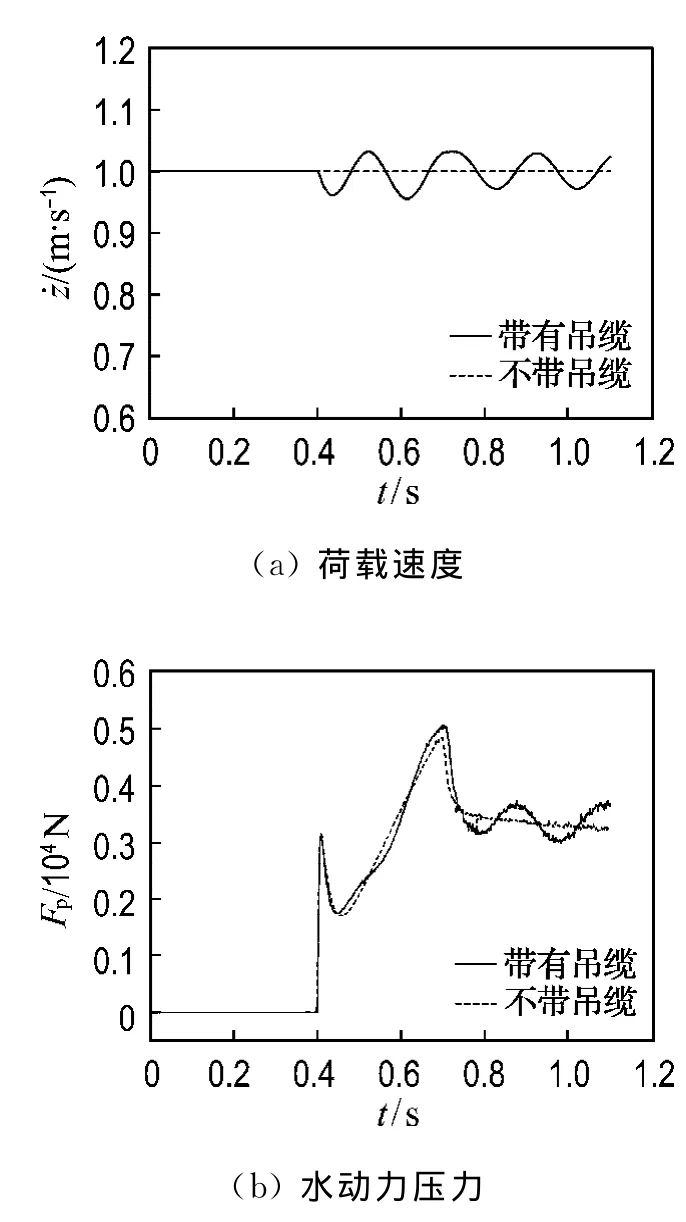
图9 有无吊缆两种入水模型的荷载速度和水动力压力的比较Fig.9 Comparison of velocity and hydrodynamic pressure of payload corresponding to two water entry models with or without wire

图10 荷载吊缆张力变化的时间历程Fig.10 Time history of wire tension on the payload

8 结 语

根据深水浮式海洋平台设计中提出的部分水动力计算问题，应用自行开发的浮体在波浪中的运动与荷载计算软件平台和相关的计算流体力学软件平台，已实现了水动力性能的数值计算，部分地得到了模型试验或相关算法的验证.部分计算模型与数值算法还期待在工程设计过程中进一步完善，更多的水动力性能计算问题尚有待于开发研究.

致谢：参与该项目研究的有博士研究生钱昆、肖越、马延德、张利军、林海花、王文华；硕士研究生汪鸿、张庆文、于得会、王建凯、吴宪法、由际昆、陶晶晶等.

[1] WANG Yan－ying.Waves and Wave loads on Offshore Structures[M].Dalian：Dalian Maritime University Press，2003

[2] WANG Yan－ying.Discussion on parameters of design waves [J]. Journal of Marine Science and Application，2008，7（3）：162－167

[3] 王言英.波浪中浮体运动与遭遇荷载计算研究[J].大连理工大学学报，2004，44（3）：313－319（WANG Yan－ying. Computation of motion and encountered loads for floating structures in waves[J].Journal of Dalian University of Technology，2004，44（3）：313－319）

[4] 王言英，钱 昆，朱仁传.辐射问题格林函数的基本解[J].大连理工大学学报，2000，40（3）：338－340（WANG Yan－ying，QIAN Kun，ZHU Ren－chuan.Essential solutions of Green function for radiation problem of floating structures in waves[J].Journal of Dalian University of Technology，2000，40（3）：338－340）

[5] QIAN Kun，WANG Yan－ying.Analysis of wave loads on a semi－submersible platform [J].China Ocean Engineering，2002，16（3）：395－406

[6] 钱 昆，王言英.基于NURBS边界元方法的波浪载荷计算研究[J].大连理工大学学报，2010，50（3）：368－373（QIAN Kun，WANG Yan－ying.Calculation of wave loads using NURBS based BEM [J].Journal of Dalian University of Technology，2010，50（3）：368－373）

[7] WANG Ge，TANG Shao－jie，SHIN Yung.A direct calculation approach for designing a ship－shaped FPSO′s bow against wave slamming load [C]//Proceedings of the Twelfth International Offshore and Polar Engineering Conference.Kitakushu：ISOPE，2002：163－168

[8] 王言英，汪 鸿.FPSO底部砰击运动与荷载预报[J].大连理工大学学报，2009，49（1）：82－87（WANG Yan－ying， WANG Hong.Prediction of bottom slamming motion and loads for FPSO [J].Journal of Dalian University of Technology，2009，49（1）：82－87）

[9] SWEETMAN B. Airgap analysis of floating structures subject to random seas：prediction of extremes using diffraction analysis versus model test results[D].Stanford：The Department of Civil and Environmental Engineering，Stanford University，2001

[10] 陶晶晶，王言英.波浪中平台气隙响应的数值计算[J].船海工程，2010，39（6）：238－240

[11] 林海花，王言英.波流共同作用下隔水管动力响应非线性分析[J].船舶力学，2009，13（2）：189－195

[12] 林海花，王言英.浪流共同作用下隔水管涡激动力响应分析[J].哈尔滨工程大学学报，2008，29（2）：121－125

[13] LIN Hai－hua， WANG Yan－ying. Discussion of mechanism and optimization for suppressing marine riser′s VIV by use of helical strakes [C]//Proceedings of the 4thAsia－Pacific Workshop on Marine Hydrodynamics（APHydro）.Taipei：NTU，2008：153－159

[14] QIAN Kun， WANG Yan－ying. Wave load calculation and analysis of mooring system for a semi－submersible in large waves[C]//Proceedings of the 4thAsia－Pacific Workshop on Marine Hydrodynamics（APHydro）.Taipei：NTU，2008：279－284

[15] 肖 越，王言英.浮体锚泊系统计算分析[J].大连理工大学学报，2005，45（5）：682－686（XIAO Yue， WANG Yan－ying. Computational analysis of the moored floating－body[J].Journal of Dalian University of Technology，2005，45（5）：682－686）

[16] 马延德，孙德壮，王言英.浮式生产储油船（FPSO）锚泊定位性能计算[J].中国造船，2006，47（4）：15－20

[17] 肖 越，王言英.三维锚泊系统时域计算分析[J].船舶力学，2005，9（5）：8－16

[18] XIAO Yue， WANG Yan－ying.The time－domain analysis for the 3－D moored system [J].China Ocean Engineering，2004，18（3）：433－444

[19] XIAO Yue， WANG Yan－ying. Analysis of deepwater mooring system for a semi－submerged drilling platform [C]//Deepwater Mooring System Concepts， Design， Analysis， and Materials（Proceedings of the International Symposium）.Houston：ASCE，2003：216－226

[20] 由际昆，王言英.深水半潜平台绷紧索系泊系统设计研究[J].中国海洋平台，2009，24（1）：24－30

[21] 吴显法，王言英.动力定位系统的推力分配策略研究[J].船海工程，2008，37（3）：92－96

[22] 于得会，王言英.吊舱推进器螺旋桨的敞水性能数值图谱[J].船海工程，2007，36（4）：38－42

[23] 张庆文，王言英.吊舱推进器及其螺旋桨的敞水性能估算[J].船海工程，2006，35（3）：1－4

[24] WANG Wen－hua，WANG Yan－ying.An improved free surface capturing method based on the cut cell mesh for water entry and exit[J].Proceedings of the Royal Society of London，Series A：Mathematical and Physical Sciences，2009，465（2106）：1843－1868

[25] 王文华，王言英.双圆柱的入水参数对水作用力的影响[J].水动力学研究与进展，2010，25（1）：23－30

[26] 王文华，王言英.圆柱在波浪中入水的数值研究[J].上海交通大学学报，2010，44（10）：1393－1399