基于AIC方法的切换神经网络模型设计

连 捷， 张 凯

（大连理工大学 电子信息与电气工程学部，辽宁 大连 116024）

0 引 言

混杂系统由于其在实际工程中的广泛应用而得到深入研究.切换系统作为一类特殊的混杂动态系统，由一组连续（或离散）时间子系统和一条决定子系统之间如何切换的切换规则组成，整个切换系统的运行情况受控于这条切换规则.对于切换系统的研究近些年已经出现了大量的成果[1～3]，包括稳定性、能控性、能观测性、控制器综合等.

神经网络由于其特有的结构与特点，早已成为很多学者重点研究的方向.又由于集成神经网络和切换神经网络的出现，神经网络的研究进入了崭新的阶段.1990年Hansen等[4]开创性地提出了神经网络集成方法，并证明通过简单地结合神经网络模型就可以显著地提高模型泛化能力.近年来集成神经网络模型被广泛应用于各个领域，许多学者也根据不同的应用情况，针对集成网络模型的逼近精度和泛化性能进行改进[5～10].在文献[11]中作者对多种集成神经网络做出了评价和比较.提出对神经网络集成实现方法的研究主要集中在两个方面，即怎样将多个神经网络的输出结果进行结合以及如何生成集成中的个体网络.2005年Huang等[12]首次将切换的思想引入神经网络模型中，提出了切换Hopfield网络模型，并给出了网络在任意切换下稳定的条件.此后，一些学者将此设计思想应用于其他网络[13、14]，也对其切换稳定性进行了分析证明.

本文主要工作是将切换思想与前向神经网络结合，构造切换神经网络模型；利用模糊C均值（FCM）聚类方法和赤池信息准则（AIC）将训练数据分类并为模型建立切换规则.

1 切换神经网络模型结构

基于AIC方法的切换神经网络模型（AICSNN）如图1所示，它由多个神经网络和一条切换规则构成.各个子网络训练结束后，制定相应的切换规则，此后模型的运行方式由切换规则决定.

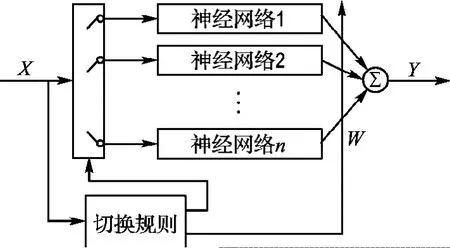
图1 切换神经网络模型Fig.1 The model of switched neural networks

在对每个神经网络训练之前要对训练数据进行聚类处理.在一些设计中，通常会选择K均值聚类，聚类后再利用每一类的数据训练神经网络.K均值聚类是将数据硬性划分到某一类中，使用这种分类方法的缺点是在结束训练后，网络在每类数据边缘处的输出达不到很高的逼近精度.尽管各个网络加权求和输出有可能减小误差，但是在边界处过大的误差也会使权值的确定出现偏差.本文使用FCM聚类方法对输入数据进行聚类.FCM聚类方法是将数据划分为n类，每个数据点用0～1的数表示属于各个类的程度.与引入模糊划分相适应，隶属度矩阵U中的元素取值范围为（0，1），并且各数据集的隶属度的和等于1.

式中：n为类别数；c为分类样本数；uij表示第i个样本属于第j类的隶属度.通过确定归为某一类的隶属度就可以将数据进行分类，各类之间可以有重叠，所以利用FCM聚类方法对样本数据分类可以解决K均值聚类导致边缘精度下降的问题，而且FCM聚类方法还可以增加每类训练数据的个数，提高网络训练精度.

2 切换规则设计

本文根据隶属度与切换网络训练误差的关系设计切换规则.

2.1 隶属度与网络训练误差的关系

在训练数据分类时首先要确定数据点归为某一类的隶属度，以作为数据分类的标准，即当数据对于某一类的隶属度大于时，则将数据归为此类.假设类别数为n，则一定要小于1/n，以保证所有数据都能分到每一类中.分类结束后，分别使用每一类数据对相应的神经网络进行训练.为了更好地设计切换规则，下面将分析隶属度与切换网络训练误差的关系.

为了说明方便，将FCM聚类用图2直观地表示.图中A统一表示非重叠部分，B统一表示重叠部分（图2中只标出了两两重叠部分）.每一类数据训练一个神经网络，比较子网络在不同区域的逼近精度.利用函数

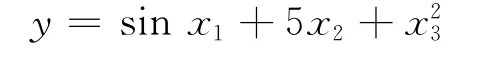
作为测试函数，将A1中的训练数据输入其他子网络，发现输出误差远大于A1训练数据对应的子网络误差.这一点也说明不同网络通过不同区域数据训练后，网络性能也会在不同区域有着明显的差别.因此在非重叠区域可以用隶属度确定需要运行的子网络.

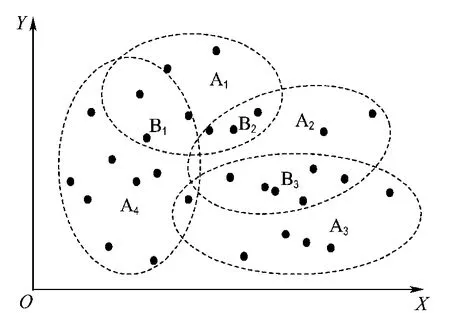
图2 FCM聚类示意图Fig.2 FCM clustering diagram

Bi（i＝1，2，3）区域为重叠区域，选择某一 Bi区域进行仿真，分析隶属度与训练误差的关系.图3为隶属度与误差的曲线图，x为Bi区域数据，e1（x）、e2（x）分别为x利用子网络1和2测试时产生的误差，u1（x）、u2（x）分别为x属于分类组1和2的隶属度，为了方便表示，将隶属度的值除以40.从图中可以看出重叠区域误差与隶属度没有固定的关系，说明在此区域子网络是否被激活不能由隶属度确定.因此在重叠区域本文选择应用网络加权求和输出的形式对目标函数进行逼近.

图3 隶属度与误差曲线Fig.3 The curves of membership and error

2.2 隐层节点和输出权值确定

AIC方法由Akaike提出，是从一类竞争模型中确定一个最佳模型的信息标准，它可以改善由网络复杂导致的过拟合现象.本文使用AIC方法[12]确定隐层节点数，并在重叠区域通过AIC的值确定子网络的输出权值，以提高重叠区域网络逼近精度.

单一网络的性能与隐层节点的数目有很大的联系，过少的隐层节点会使网络逼近精度达不到要求，过多的隐层节点又会导致过拟合.所以选择合适的隐层节点数有助于改善网络的性能.在确定隐层节点数时需要同时考虑测试数据均方误差和AIC值，相对较小的测试数据均方误差值和AIC值对应的隐层节点数即为所选.

AIC值可通过下式计算：

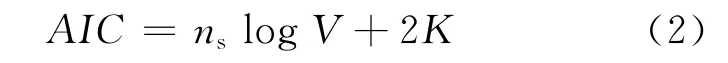
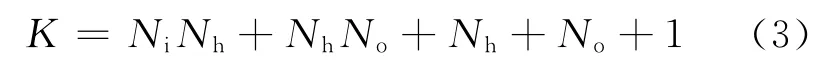
其中Ni为神经网络输入节点个数，Nh为隐层节点个数，No为输出节点个数，NiNh＋NhNo即为所有权值个数，Nh＋No即为所有阈值个数.

利用AIC方法确定重叠区域子网络的输出权值.用分类后的数据计算出每一类的AIC值，用Δj表示各子网络与最优网络AIC值之间的差异，Δj＝AICj－minAIC，minAIC表示所有网络计算AIC值中最优的.定义

其中β值用来决定Δm的范围，小的β值表示每个Δm差别不大，大的β值表示每个Δm有较大差别，这里β值由下式确定：

Divi＝为第i个网络的输出值为网络输出的平均值.由以上这些计算结果确定权值为

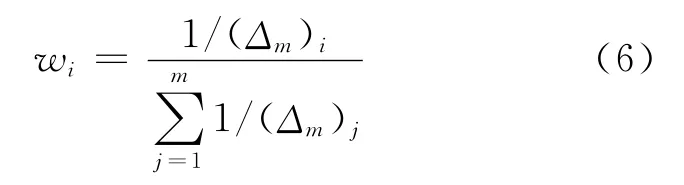
其中wi为第i个神经网络输出的权值.

2.3 设计切换规则

根据上面的分析，设计相应的切换规则，尽量使每个子网络在最优的区域工作.

假设训练数据被分为n类，聚类中心为C＝（c1c2…cn），ci为第i类聚类中心.有m组测试数据X＝（x1x2…xm），按照下式计算测试数据与每一类的隶属度：

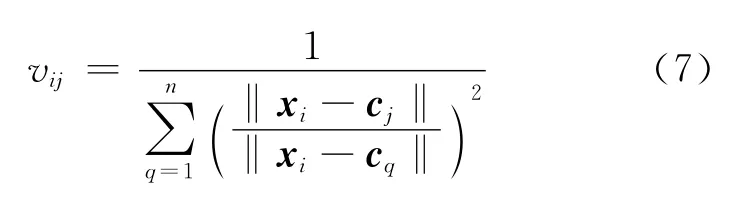
其中vij表示第i个测试数据与第j个聚类中心的隶属度.

切换网络的输出为

式中：σ（xi）＝ ｛j｜vij＞，j＝1，2，…，n｝，为当输入数据为xi时的切换规则；σz∈σ（xi）表示σz为σ（xi）集合中的元素；fσz（xi）为被激活子网络输出；wσz为激活网络对应权值，通过AIC方法确定，且

从切换规则的形式可以看出，不同的输入数据经过切换规则后会激活不同的子网络，同时会计算出激活网络对应的输出权值.当输入数据在非重叠区域时，σ（xi）中仅有一个元素，表示此时仅有一个网络被激活，相应的输出权值wσz＝1.当输入数据在重叠区域时，σ（xi）中会有多个元素，表示有多个子网络被激活，切换规则会根据此时激活的子网络计算出对应的输出权值，切换网络输出Y由σ（xi）中所有元素对应的子网络输出加权求和得到.

3 切换神经网络仿真

仿真1 选择Matlab中的peak函数进行仿真测试，peak函数形式为

在peak函数中加入均值为0、方差为0.05的噪声，选择121组数据（x1，x2）作为训练数据，其中x1，x2∈[－3，3].另外生成100组数据（x1，x2）作为测试数据用来测试网络性能.采用FCM方法将训练数据分为4类，对每一部分建立子网络模型，选择网络模型为BP网络，利用AIC方法选择隐层节点数为15.每个子网络训练30次.网络训练完成后，根据训练数据隶属度按照AIC方法生成切换规则，最后利用测试数据对网络进行测试.

将基于AIC方法的切换神经网络模型（AICSNN）与单一网络模型和基于AIC方法的集成神经网络模型（AIC－ENN）进行比较，表1列出了各模型均方误差（MSE）在最小值、平均值和标准差三方面的比较结果，表中数据为进行20次仿真后的计算结果.图4给出了测试数据经过AIC－SNN模型仿真后与期望值的比较结果（yp为期望值，ya为实际值）.

表1 模型比较结果（仿真1）Tab.1 The comparison result of different models（Simulation 1）

图4 AIC－SNN对于测试数据的仿真结果（仿真1）Fig.4 The simulation results of AIC－SNN for the test data（Simulation 1）

从表1可以看出基于AIC方法的集成神经网络模型在逼近准确性方面要比其他两种模型效果好.图4中数据点都在倾斜角为45°的直线附近分布，这也说明了测试数据经过AIC－SNN模型仿真后，实际值较好地逼近了期望值.

仿真2 选择Friedman＃1数据集作为仿真对象，数据集根据下式产生：

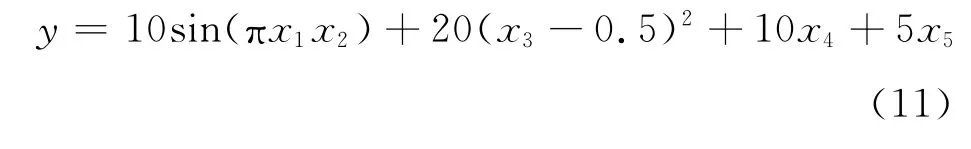
每个输入向量含有5个分量，其中xi（i＝1，2，…，5）是0～1的随机数，选取200组数据作为训练数据，在训练数据中加入均值为0、方差为1的高斯噪声.选取不含噪声的200个数据用来测试网络性能.采用FCM方法将训练数据分为4类，对于每一部分建立子网络模型，利用AIC方法选择隐层节点数，子网络选用隐层节点为10的BP网络，每个子网络训练30次.网络训练完成后，根据训练数据隶属度按照AIC方法生成切换规则，最后利用测试数据对网络进行测试.

表2给出了各模型均方误差的比较结果，表中的数据为进行20次仿真后的平均值.图5给出了测试数据经过AIC－SNN模型仿真后与期望值的比较结果.

表2 模型比较结果（仿真2）Tab.2 The comparison result of different models（Simulation 2）

从表2可以看出，AIC－SNN模型无论在训练数据准确性还是测试数据准确性方面都比AICENN模型效果好.图5中数据点的分布情况也说明了测试数据经过AIC－SNN模型仿真后，实际值较好地逼近了期望值.

图5 AIC－SNN对于测试数据的仿真结果（仿真2）Fig.5 The simulation results of AIC－SNN for the test data（Simulation 2）

仿真3 利用UCI数据集中的Servo数据进行仿真.该数据有167组，每组数据有4个类别属性.利用130组数据作为训练数据，37组数据作为测试数据.利用AIC方法选择隐层节点数为15的BP网络，每个子网络训练30次.网络训练完成后，根据训练数据隶属度按照AIC方法生成切换规则，最后利用测试数据对网络进行测试.

表3为各模型均方误差的比较结果，表中的数据为进行20次仿真后的平均值.图6给出了测试数据经过AIC－SNN模型仿真后与期望值的比较结果.

从表3可以看出，AIC－SNN训练数据均方误差在三方面比较中都优于前两个模型，测试数据均方误差除了最小值稍高于AIC－ENN模型外，平均值和标准差都要优于前两个模型，说明AICSNN模型有较好的逼近精度，较前两个模型还是有一定的改善.从图6也可以看出实际值较好地逼近了期望值.

表3 模型比较结果（仿真3）Tab.3 The comparison result of different models（Simulation 3）

图6 AIC－SNN对于测试数据的仿真结果（仿真3）Fig.6 The simulation results of AIC－SNN for the test data（Simulation 3）

4 结 论

本文构建了切换神经网络模型，利用FCM聚类方法和AIC方法为模型建立了切换规则.将数据分区域考虑，尽量应用子神经网络训练效果好的区域，增强了网络的逼近能力.由于切换规则的使用，更好地利用了各个子网络在特定区域具有较高逼近精度的特点，降低了模型工作复杂度，也改善了由于某些网络训练效果不佳带来的输出偏差.仿真结果表明，基于AIC的切换神经网络模型不仅能降低训练数据的误差，而且能较好地降低测试误差，使网络有较好的逼近性能.但是，网络中还有一些需要人为设定的参数，比如分类隶属度和分类数目，所以还需进一步完善和深入研究.

[1] ZHAO Jun，HILL D J.On stability，and L2－gain andH∞control for switched systems[J].Automatica，2008，44（5）：1220－1232

[2] LIAN Jie，ZHAO Jun.Output feedback variable structure control for a class of uncertain switched systems[J].Asian Journal of Control，2009，11（1）：31－39

[3] 付主木，费树岷，龙 飞.一类线性切换系统H∞状态反馈控制：LM I方法[J].控制与决策，2006，21（2）：197－200

[4] HANSEN L K，SALAMON P.Neural network ensembles[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，1990，12（10）：993－1001

[5] ZHOU Zhi－hua， WU Jian－xin， TANG Wei.Ensembling neural networks：Many could be better than all[J].Artificial Intelligence，2002，137（1－2）：239－263

[6] SRIDHAR D V，SEAGRAVE R C，BARTLETT E B.Process modeling using stacked neural networks[J].AIChE Journal，1996，42（9）：2529－2539

[7] ISLAM M M， YAO Xin， MURASE K. A constructive algorithm for training cooperative neural network ensembles[J].IEEE Transactions on Neural Networks，2003，14（4）：820－834

[8] YU Lean， LAI Kin－keung， WANG Shou－yang.Multistage RBF neural network ensemble learning for exchange rates forecasting[J]. Neurocomputing，2008，71（16－18）：3295－3302

[9] ZHAO Zhi－ye，ZHANG Yun，LIAO Hong－jian.Design of ensemble neural network using the Akaike information criterion[J].Engineering Applications of Artificial Intelligence，2008，21（8）：1182－1188

[10] 熊智华，王 雄，徐用懋.一种利用多神经网络结构建立非线性软测量模型的方法[J].控制与决策，2000，15（2）：173－176

[11] 周志华，陈世福.神经网络集成[J].计算机学报，2002，25（1）：1－8

[12] HUANG He， QU Yu－zhong， LI Han－xiong.Robust stability analysis of switched Hopfield neural networks with time－varying delay under uncertainty[J].Physics Letters A，2005，345（4－6）：345－354

[13] LI Ping，CAO Jin－de.Global stability in switched recurrent neural networks with time－varying delay via nonlinear measure[J].Nonlinear Dynamics，2007，49（1－2）：295－305

[14] LOU Xu－yang， CUI Bao－tong. Delay－dependent criteria for global robust periodicity of uncertain switched recurrent neural networks with timevarying delay [J].IEEE Transactions on Neural Networks，2008，19（4）：549－557