大平面砂轮磨齿特点与磨损规律
2011-06-05凌四营,王立鼎,马勇,王晓东
凌 四 营, 王 立 鼎, 马 勇, 王 晓 东
(大连理工大学 精密与特种加工教育部重点实验室,辽宁 大连 116024)
0 引 言
大平面砂轮磨齿机具有结构简单、便于精化改造以及传动链的刚度高等特点,广泛用于标准齿轮及齿轮刀具的精密制造领域.20世纪80年代,长春光学精密机械研究所成功改装了Y7431型大平面砂轮磨齿机,研制出了2级精度的基准标准齿轮[1~3],达到了国际先进技术水平.文献[4]指出大平面砂轮磨齿机的磨齿精度仍可进一步提高.
目前,国内学者对大平面砂轮磨齿机的研究主要集中在机床的改造方面[5],热力学和动力学方面的研究还很少涉及.在超精密齿轮的磨齿过程中,温度引起的零件热变形占有相当大的比例[6],磨削中的颤振对磨齿精度的提高也有一定的影响[7、8].建立磨齿热力学模型和动力学模型,分析磨削参数对磨削温度和磨削振动的影响以提高大平面砂轮磨齿精度,这一方面有待于开展进一步研究.
大平面砂轮磨齿过程中,齿面上某一点砂轮的线速度vs和工件的进给速度vw是不断变化的,这给大平面砂轮磨齿机磨削模型的准确建立带来一定的困难.本文基于机构运动学首先分析大平面砂轮磨齿过程中砂轮转速和工件进给速度的变化规律,为磨齿热力学和动力学模型的准确建立提供理论依据,然后对大平面砂轮的磨损规律进行探索与研究,旨在指导超精密齿轮的磨齿实践.
1 大平面砂轮的磨齿特点
1.1 机床工作原理
大平面砂轮磨齿是依据齿条与齿轮啮合的原理,以大平面砂轮的工作面作为“假想齿条”的一个齿面,用展成法来加工齿轮的.机床的展成运动一般有两类:一类是利用钢带与滚轮作纯滚动形成展成运动,例如Gleason集团研制的SRS 405数控剃齿刀磨齿机及国产的Y7432型磨齿机等;一类是利用渐开线凸轮与挡板形成展成运动,美国的National Tool型、前苏联的589系列磨齿机及国产的大平面砂轮磨齿机都属于这一类型.Y7125型大平面砂轮磨齿机的工作原理如图1所示.
机床的展成系统与分度系统的动力源来自同一台电机.电机输出的运动经过塔轮变速后,一路由锥齿轮、软轴、分度蜗杆蜗轮、马氏机构及分度挂轮来驱动分度盘作间歇分度运动;另一路则经过蜗杆蜗轮机构、曲柄摇杆机构和五杆高副机构来驱动渐开线凸轮作往复摆动,进而形成磨齿的展成运动.被磨齿轮的齿距精度主要由机床分度盘的齿槽精度来保证,而展成运动的精度则与头架安装角αy的调整精度及机床展成系统的精度有关.

图1 Y7125磨齿机的工作原理Fig.1 Working principle of grinder Y7125
1.2 砂轮磨齿线速度
大平面砂轮的磨削面是垂直于砂轮回转轴线的一个侧面,因此,磨削点的线速度与该点的回转半径有关.砂轮工作面与齿面的接触区域为一圆环形区域,它的宽度由两部分组成:有效接触宽度B(对应于磨削齿轮渐开线的部分)和额外切入深度h(对应于磨削齿轮的过渡曲线部分),如图2所示.

图2 大平面砂轮的工作区Fig.2 Working area of large plane grinding wheel
约定当机床头架滑到最低点位置时,齿轮轴线与大平面砂轮工作面之间的最小距离为E.为了能加工出完整的渐开线,此位置砂轮与齿轮的接触点应对应于齿轮渐开线的最低点.当被磨齿轮的根圆半径大于其基圆半径时,E为一正值;反之,E为零.根据运动的相对性,假设砂轮移动,齿轮转动.砂轮在位置Ⅰ时,砂轮磨削齿轮渐开线的最低点i,在位置Ⅱ时,砂轮磨削齿轮渐开线的最高点e.当rf>rj时,E的计算如图2所示,显然有
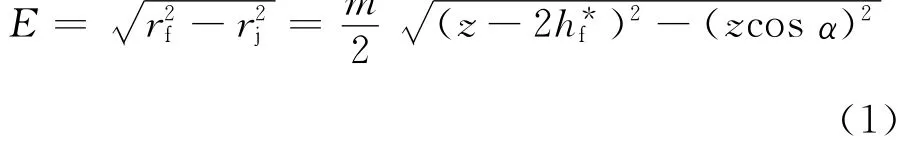
式中:rf表示齿轮根圆半径;m表示齿轮的模数;z表示齿数;hf*表示齿根高系数;α表示压力角.
如果rf≤rj,则取E=0.
由图2中的几何关系可得到砂轮有效接触宽度B的表达式为

式中:ρe表示渐开线在齿顶处的曲率半径.
将上式写成渐开线任意点的曲率半径ρx的函数为

由于大平面砂轮工作时沿齿宽方向上没有相对运动,为了确保能磨出标准齿高的齿轮,砂轮齿宽中截面上需要额外切入h,其大小为

式中:R表示新砂轮的半径,R=200 mm;Rw表示砂轮磨损后半径上的减小量(mm);b表示齿宽(mm).
设砂轮的转速为ns(r/min),则磨削点对应砂轮的线速度vs(m/s)可表示为

可以看出,大平面砂轮磨齿过程中磨削点的线速度从齿根到齿顶是线性减小的.由于砂轮的有效接触宽度B远小于砂轮的半径(对于Y7125磨齿机来说,一般小于20 mm),砂轮线速度的变化范围不明显.
1.3 工件进给速度
大平面砂轮磨齿过程中,工件进给速度vw是一个接近正弦曲线的变量,它不但与机床的运动特性有关,还与齿坯参数和磨齿参数有关.首先计算被磨齿轮渐开线的长度(如图3所示).
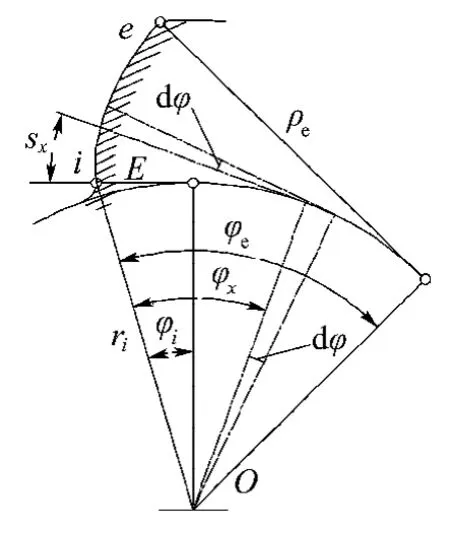
图3 渐开线的长度计算Fig.3 Calculation of the length of the involute
根据渐开线的发生原理可知,渐开线的展开角度φ与展成长度ρ之间满足下述关系式:

根据渐开线的长度公式可知
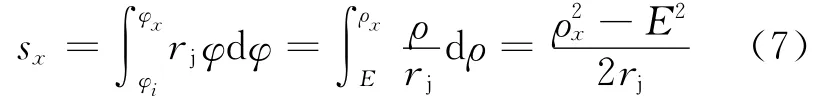
对上式进行求导可得
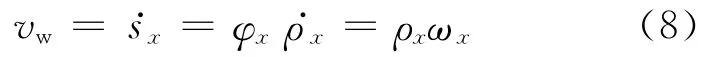
由式(8)可知,工件任意一点的进给速度等于工件在此点处的展开角φx与工件在砂轮工作面法向速度分量的乘积;也可以表示为磨削渐开线任意点的曲率半径ρx与头架在此时角速度ωx的乘积.
通过对机床传动机构列位移方程组和速度方程组进行求解能够计算出头架的角速度ωx.但是由于马刀长度、曲柄长度、挡板位置以及渐开线凸轮工作段的使用位置都是可以调整的,另外待求解的方程数量较多,解析求解比较困难.对于磨削某一特定参数的齿坯,可借助于NX软件中的运动仿真模块进行仿真求解.不同齿坯参数和机床参数对应的头架角速度也不同,但其随时间的变化趋势是一致的.在头架由低点运动到高点的过程中,ρx由E逐渐增大.由于头架运动过程中还包含着分度运动,一般来讲ρx的最大值要大于2ρe(ρx可通过调整曲柄长度进行控制).ωx由0逐渐增大到某一值后又逐渐减小至0.头架角速度的最大值一般出现在磨削齿轮渐开线最高点e的附近.因此,工件进给速度vw在磨齿过程(不包括分度过程)中是由0非线性增大的.另外,vw的大小还与塔轮的传动比有关.
2 大平面砂轮的磨损规律
由大平面砂轮磨齿机的工作原理可知,大平面砂轮的磨损规律与普通磨床砂轮的磨损规律不同.由图2可知,大平面砂轮的环形工作区域由两部分组成:磨削齿轮有效渐开线的部分(定义为WB区,宽度为B)和磨削齿轮齿根过渡曲线及砂轮径向额外切入部分(定义为Wh区,宽度为h).对大平面砂轮而言,上述两部分的磨损规律有所不同.由于砂轮Wh区主要用来磨削齿根过渡曲线及齿根圆角,磨损规律复杂,且不影响被磨齿轮有效渐开线的磨削,因此,本文只讨论砂轮WB区的磨损规律.
2.1 建立数学模型
联立式(3)和(7)可得
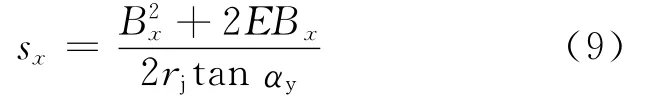
对上式进行微分可得
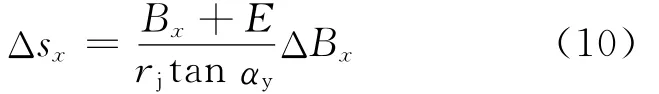
由于ΔBx的系数是砂轮与齿面接触位置B x的函数,说明磨削某一微小长度的渐开线对应的砂轮使用宽度是逐渐变化的.从齿根到齿顶的磨削过程中,磨削同一长度的渐开线对应于砂轮的使用宽度逐渐变小,从而说明在此过程中砂轮磨损程度越来越严重.大平面砂轮与齿轮渐开线接触位置的对应关系见图4.定义单位体积齿轮磨除量Vw与砂轮磨损量Vs的比值为齿轮的磨削率K,它的大小与被磨齿轮的硬度、材料、砂轮的品质(包括磨料种类、磨粒大小、磨具的硬度、结合剂种类等)、进刀量大小以及砂轮的修整质量(砂轮的修整量、修整速度及金刚石笔的品质)有关.在特定工况下,K为常数.定义砂轮工作面法向磨损量为By.

图4 砂轮与渐开线接触位置对应关系Fig.4 Corresponding relation between the touching lines of grinding wheel and gear involute
在磨齿过程中,齿轮的磨削率K满足下式:

式中:n表示砂轮修整后磨削轮齿的数量;Δf表示砂轮的进刀量.
联立式(10)、(11)可得

通过上式可以看出,By是B x的增函数,这也说明砂轮在磨齿过程中由齿根到齿顶磨损量逐渐增大,定义砂轮磨损系数为

则式(12)可写成

2.2 实 验
在恒温室里,使用Y7125大平面砂轮磨齿机进行磨齿实验,相关齿坯参数(标准齿轮)、机床参数及砂轮参数如表1所示.

表1 磨齿的主要参数Tab.1 The main parameters of gear grinding
实测砂轮半径方向上的减小量Rw=3 mm,根据式(1)、(2)和(4)可计算出E=11.2858 mm,B=4.0131 mm,h=0.2540 mm.
则By/Kc与Bx的关系为

用线性多项式拟合后可近似表示为

其中拟合均方差为6.93×10-5,如图5所示.

图5 砂轮工作面B y/K c与Bx的关系Fig.5 The relation between By/K c and Bx
由图5可知,砂轮工作面法向磨损量B y/Kc与接触位置Bx基本上呈线性变化.这也说明大平面砂轮在均匀磨齿的过程中其工作面的磨损程度是不均匀的.由齿根到齿顶,砂轮的磨损程度逐渐变大.
为了减小齿廓偏差对实验结果的影响,尽量选择齿廓形状偏差和齿廓倾斜偏差小的齿坯进行磨齿实验.精修砂轮,使砂轮工作面环形区域的颜色均一.采用精磨工况进行均匀磨齿,一段时间后发现砂轮工作面的颜色沿砂轮半径方向由外向内逐渐变黑(如图6所示),从而验证了大平面砂轮在均匀磨齿过程中磨损程度是不均匀的.

图6 磨齿实验后砂轮的形貌Fig.6 Morphology of the wheel after grinding
3 分析与讨论
在磨齿过程中,砂轮工作面的平面度及磨齿机渐开线凸轮的面形精度对齿轮的齿廓精度影响较大.对于特定的渐开线凸轮而言,可通过实验法选取凸轮面形误差较小的区域作为工作段,但使用此法减小被磨齿轮的齿廓偏差是有限的.除此之外,提高大平面砂轮的品质及修整质量,尤其是提高砂轮工作面的平面度可大幅度减小被磨齿轮的齿廓偏差.
大平面砂轮的磨齿特点决定了其工作面磨损程度的不均匀性,从而增大了砂轮工作面的平面度,致使被磨齿轮产生较大的齿廓偏差.产生的齿廓倾斜偏差可通过微调头架安装角αy进行误差补偿,调整量约为

然而,由于最后一次进刀砂轮工作面的磨损量By的影响因素很多,通过调整头架安装角的方法不能做到完全补偿.为减小被磨齿轮的齿廓偏差,减小砂轮工作面的法向磨损量B y并维持相对稳定的B y值,可采取如下改进措施:
(1)选择品质合适的砂轮,尤其是砂轮磨具的硬度.硬度太大的砂轮其自锐性能差,砂粒磨钝后也不易脱落,致使磨削性能下降.硬度太小的砂轮磨损量大,砂粒脱落后砂轮工作面的平面度有所增大,影响磨齿精度.根据经验,精密磨齿中选择软3(J级)硬度的砂轮可得到较好的磨削性能和较高的磨齿精度.
(2)微量磨削.由式(16)可知,微量磨削有利于减小砂轮工作面的磨损量.微量磨削还可以:①减小磨齿过程中的磨削力,降低砂轮与齿轮的接触刚度;②减少磨齿产生的热量,降低齿面被烧伤的风险;③减小砂轮工作面及齿面误差的复映量,提高校正齿形的能力.对于磨削2~1级精度的超精密齿轮,微量进刀量建议为0.5μm.
(3)勤修精修砂轮.砂轮的修整质量还与金刚石笔的品质与修整方法有关.经常改变金刚石笔相对于砂轮的位置,慢速均匀地修整砂轮有利于提高砂轮的修整质量及磨齿性能.
(4)选择合适的停车时刻.砂轮使用一段时间后会出现半塞实状态,此时的砂轮工作面颜色呈灰色,磨粒的切削刃开始变钝,但砂轮仍具有良好的表面精度及一定的磨削性能.砂轮过于锋利则被磨齿轮的齿面粗糙度偏大.而磨削刃钝化又会:①增大砂轮的磨损;②塞实砂轮,降低磨粒的切削性能;③增大磨齿烧伤的风险.实验表明:在砂轮半塞实状态下停车,既能使齿面获得理想的表面粗糙度,又不会使砂轮过度磨损而影响齿轮的齿廓加工精度.
应用上述改进措施选择表1中的参数进行精密磨齿实验.平衡温度后在基准级渐开线测量仪上测量被磨齿轮的齿廓偏差,磨齿与测量设备如图7所示.

图7 磨齿与测量设备Fig.7 Equipment of grinding and measuring
选取齿轮对称位置的4个齿进行齿廓偏差测量,测试结果如图8所示.
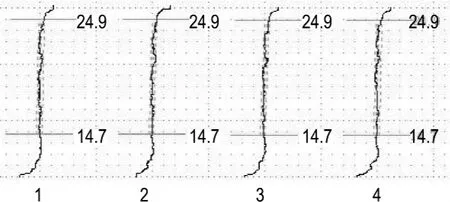
图8 齿廓测量曲线Fig.8 Measurement curve of the gear profile
将测试结果与1级精度(ISO 1328-1:1955)进行比较,结果如表2所示.
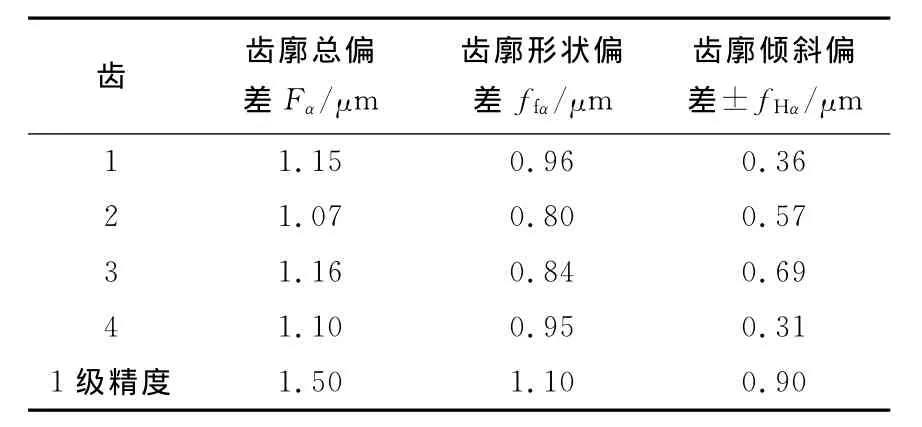
表2 测试结果Tab.2 The measurement results
由表2可知,应用实验室精化后的Y7125型磨齿机,并采用超精密磨削工艺,可研制出具有国际领先技术水平的1级齿廓精度的超精密齿轮.
4 结 论
(1)推导出了大平面砂轮磨齿中砂轮线速度与工件进给速度的公式,为磨齿热力学和动力学模型的准确建立提供了理论依据.
(2)研究了大平面砂轮的磨损规律,得出在均匀磨齿过程中砂轮的磨损量从齿根到齿顶逐渐增大的结论,提出应选择品质合适的砂轮、微量磨削、勤修精修砂轮及在半塞实状态下停车等措施以提高被磨齿轮的齿廓精度.
(3)采用提出的超精密磨齿工艺进行磨齿实验,被磨齿轮的齿廓精度可达ISO 1328-1:1995中的1级精度.
[1]王立鼎,卢占山.高精度小模数标准齿轮的磨齿[J].现代制造工程,1980(5):20-23
[2]王立鼎.在用分度盘分度的磨齿机上被磨齿轮周节精度的研究[J].精密制造与自动化,1981(3):35-41
[3]王立鼎,卢占山.模数2基准标准齿轮的研制[J].光学精密工程,1982(4):28-34
[4]王立鼎,凌四营,马 勇,等.精密、超精密齿轮的加工方法[J].光学精密工程,2009,17(2):321-325
[5]周鸿德.用数控技术改造Y7125磨齿机砂轮修整器[J].组合机床与自动化加工技术,1997(10):25-27
[6]费业泰,李广珂.精密技术中热变形误差理论研究与探讨[J].中国机械工程,2008,19(15):1765-1769
[7]ALTINTAS Y, EYNIAN M, ONOZUKA H.Identification of dynamic cutting force coefficients and chatter stability with process damping[J].CIRP Annals-Manufacturing Technology,2008,57(1):371-374
[8]KHACHAN S,ISMAIL F. Machining chatter simulation in multi-axis milling using graphical method[J].International Journal of Machine Tools and Manufacture,2009,49(2):163-170
