提高地铁车站结构抗震能力的理论及数值分析

还 毅，方 秦，柳锦春，陈 力，杜茂林

(解放军理工大学，南京 210007)

在强地震荷载作用下，建筑结构往往破坏十分严重。我国地处环太平洋地震带与欧亚地震带之间，地震活动频繁，是世界上地震危害最重的国家之一。随着城市化的发展，大规模开发利用地下空间已经成为一种必然趋势，近几十年来，地下结构在城市建设、交通运输、国防工程等各个领域得到了广泛应用，尤其在城市建设方面，以地下铁道为骨干的大运量快速公共交通系统已经成为城市客运交通问题的重要解决途径。通常认为，地下结构赋存于岩土介质中，受周围土体约束，具有较好的抗震性能，然而1995年1月17日日本南部发生了里氏7.2级的“阪神地震”，神户地区大量结构发生破坏，大开地铁车站的破坏尤为严重，中柱大量折断(见图1)，混凝土脱落，钢筋屈曲，顶板塌陷，侧墙出现大量宽大裂纹，造成地铁上方的国道路基大量塌陷，塌陷深度最高达到2.7 m，导致日本南部交通瘫痪。类似的震害教训表明:强地震时，地下结构周围地基土的变形很大，可能使地下结构的薄弱环节破坏，进而影响整个地下结构体系的稳定性。因此，研究地下结构在地震载荷作用下的动力响应、评价结构在地震作用下的承载能力、提高结构的抗震能力已成为结构工程领域十分关注的问题。

图1 阪神地震中大开地铁车站中柱的坍塌破坏Fig.1 Collapse of mid-columns of Daikai subway station in kobe earthquake

地铁车站等大断面地下结构的破坏主要是由于某些重要构件的损坏引起的，引起大开地铁车站破坏最主要因素是中柱的坍塌，提高这类重要地下结构的抗震能力首先要提高其关键构件的抗震性能。提高构件的承载能力通常是从材料、截面形状等方面入手，而以往的研究［1－5］表明:在构件端部合理设置弹簧和阻尼器可以有效提高构件的抗力。工程设计中可以将碟形弹簧与铅芯橡胶支座串联构成三维隔震支座，隔震支座能够提供一定的弹簧刚度和阻尼，碟形弹簧隔离竖向地震，铅芯橡胶隔离水平地震，这样既可以保证建筑物在水平地震下的安全性，又可以避免地震水平作用减弱后，由于竖向地震作用成为主要地震作用而导致建筑结构发生破坏。三维隔震支座的设置方法与具体参数参照文献［1］。

然而，具有弹簧和阻尼器支承构件在外部动载荷作用下的动力响应分析要比刚性支承构件复杂得多，主要原因是边界位移会引起附加惯性力，从而影响结构变形，其动力响应不仅取决于结构的固有特性，还与支承条件密切相关，完全刚性支承理论已不适用。正确分析结构的动力特性以及支承边界条件对结构动力响应的影响，对于结构计算与设计提供理论依据，具有重要的工程意义。一些学者对此问题展开了研究，方秦等［2］应用梁在刚性支承条件下动力响应的现有结论和第二类拉格朗日方程，分析了爆炸荷载作用下端部弹簧和阻尼器支承对梁动态响应的影响;杜茂林等［3］采用理论与数值分析方法分别研究了门上和端部设置弹簧和阻尼器提高防护门抗力的可行性和有效性;宋春明［4－5］建立了动边界梁的力学模型，研究了柔性动边界梁、拱在横向撞击作用下的动力响应，所谓柔性动边界梁即具有特定约束梁，这些约束通常表现为弹簧支承刚度和阻尼特征。然而目前的研究主要集中在柔性动边界梁的固有振动分析和爆炸冲击作用下的动力响应分析方面，对地震荷载作用下弹簧和阻尼器支承构件的动力响应研究却十分鲜见。

本文对端部弹簧与阻尼器支承梁的动力分析方法［2］进行改进，使其适用于地震作用下柔性动边界梁动力响应方面的研究，并应用改进方法分析了地震作用下端部弹簧与阻尼器支承柱子的动态响应。在理论分析基础上，以1995年日本阪神地震中破坏最为严重的大开地铁车站为研究对象，采用ABAQUS有限元分析程序，进一步分析了在非线性条件下柱子端部设置弹簧和阻尼器对提高地铁车站结构抗震能力的影响。

1 提高地铁车站结构抗震能力的作用机理分析

1.1 地震荷载作用下柔性动边界梁理论分析模型

结构中的关键构件一旦发生破坏，结构的整体稳定性将会受到影响，而地铁车站等大空间地下结构在地震荷载作用下受力情况相当复杂，既受到水平地震、竖向地震的作用，还会受到上部覆土、结构本身自重的影响。为了减轻地震危害，可以将地面建筑隔震机理应用于地下结构，在构件端部设置隔震器，于是该问题可简化为如图2所示的地震荷载作用下柔性动边界梁动力响应分析模型，图中梁同时承受地震加速度与轴力作用。

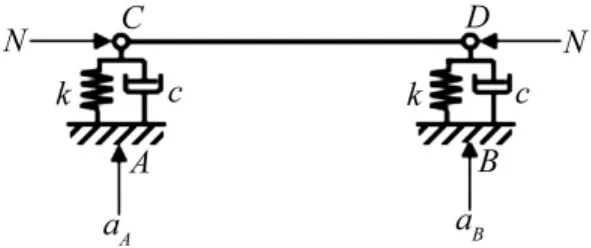
图2 弹簧阻尼支承梁分析模型Fig.2 Analytical model of beam with flexible supports

t时刻，距梁端Cx处的位移可表示为端部位移所引起的该点的位移与端部变位为零时该点的位移之和，即:

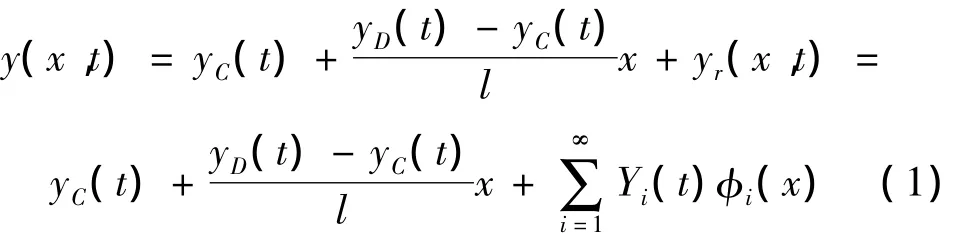
其中，yC(t)和yD(t)分别为梁端点C和D的竖向位移，一般情况下yC(t)≠yD(t);yr(x，t)是端点C和D变位为零时梁x处的竖向振动位移，可写为yr(x，t)=Yi(t)φi(x)，Yi(t)为动力函数，φi(x)为梁的振型函数，可表示为 φi(x)=Aisinδx+Bicosδx+Cisinhεx+Dicoshεx，将简支梁的边界条件代入上式，可将振型函数简化为 φi(x)=Aisinδx，其中

由梁和不计质量的弹簧和阻尼器组成的系统的动能T可写为:

系统势能V由弹簧的弹性势能和梁的势能组成，而梁的势能由弯曲应变能和轴向压缩时的变形能组成:

其中，yA(t)和yB(t)分别为端部支承处的竖向位移，N(x)为任一截面的轴向应力，E为材料的弹性模量，A为截面面积。

对应于广义坐标yC(t)的广义力为－c()，对应于广义坐标yD(t)的广义力为－c()，对应于广义坐标Yi(t)的广义力为零，其中c为端部支承的阻尼系数。

系统的拉格朗日函数可写为:

将式(2)～式(4)代入第二类拉格朗日方程:

其中，qj为广义坐标(yC(t)，yD(t)和Y)。即:

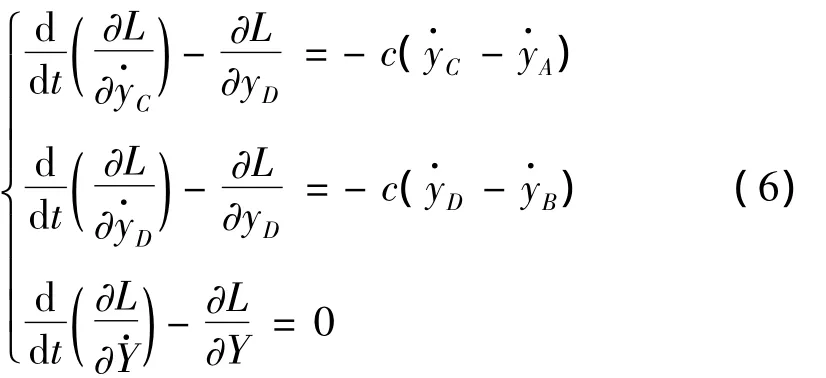
方程(6)为常微分方程组，可用Runge-Kutta方法求解。方程具体建立和求解借助于软件Maple来完成。

1.2 理论分析模型有效性的验证

为了检验地震荷载作用下柔性动边界梁动力响应分析模型的可靠性，本文选取一根常规尺寸柱作为算例进行分析，取柱高l=2 m，柱截面为b×h=0.1 m×0.1 m，弹性模量E=32500 MPa，支座两端承受地震加速度荷载和轴力作用，轴力大小取为5000 N，如图3所示，支座A处输入的地震加速度为1995年阪神地震中的实测加速度(Kobe波)，其时程曲线如图4所示，频谱分析见图5。通常地震波由基岩处通过土体向上传播过程中会产生一定程度的放大或衰减，因此，地铁车站中柱两端承受的地震加速度往往是不同的，故将支座B处输入的加速度峰值调整为支座A处的0.8倍。总弹簧刚度系数取为k=800 N/m，总阻尼系数取为c=100 Ns/m。结构动力分析中，若只需求最大动位移和最大动弯矩，可只考虑少数主振型，甚至只考虑一个最低主振型，忽略高次振型的影响。图6是选取构件第一振型的分析方法、选取前三个振型的分析方法与ABAQUS有限元计算的柱跨中绝对位移时程曲线。ABAQUS有限元计算参数与理论分析模型的计算参数一致。由图6可知，三种方法计算得出的构件跨中位移基本一致，误差不超过1%。而选取单自由度分析方法和三自由度分析方法的计算结果基本一致说明了取构件的第一振型已具有足够精度。为了进一步验证分析方法的可靠性，同样选取了2 Hz的正弦波、Taft波以及EL-Centro波进行了分析，分析得出的结论与Kobe波分析结论一致，限于篇幅，文中不一一列举。

1.3 主要影响因素分析及讨论

1.3.1 弹簧和阻尼器支承的影响分析

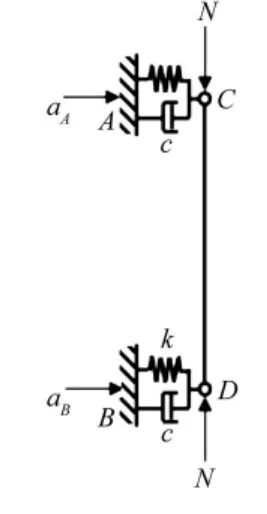
图3 弹簧阻尼支承柱分析模型Fig.3 Analytical model of column with supports of spring and dampers

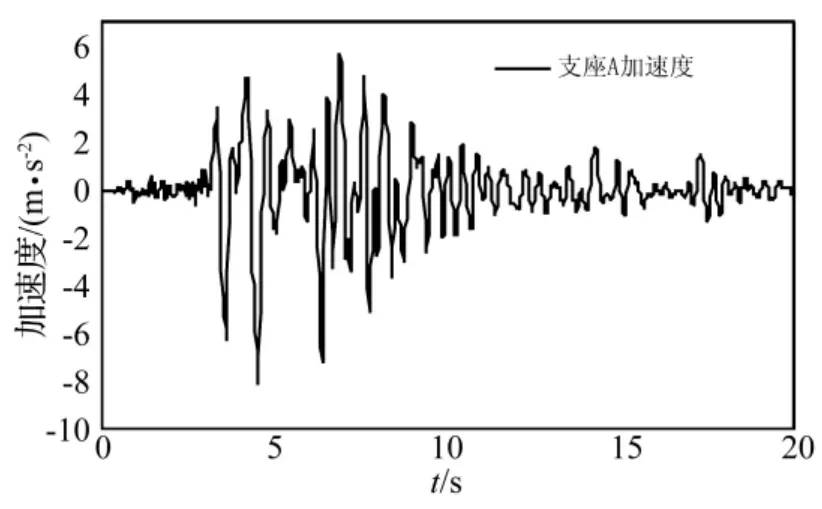
图4 支座A输入加速度时程曲线Fig.4 Acceleration-time history applied at the end of A

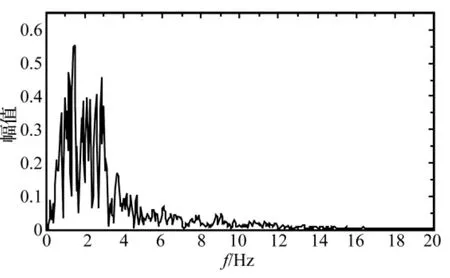
图5 支座A输入加速度频谱分析Fig.5 Frequency spectrum of acceleration applied at the end of A

为了检验端部设置弹簧和阻尼器对提高柱子抗震能力的效果，本文以大开地铁车站的中柱为算例，采用上述理论分析模型进行计算分析。取柱长l=5.5 m，柱截面为 b×h=0.4 m ×1.0 m，弹性模量 E=32500 MPa，轴力N=0，弹簧刚度k=20000 N/m，阻尼系数c=10000 Ns/m，选取Kobe波作为支座承受的加速度荷载。

图7为地震加速度作用下有弹簧和阻尼器支承和无弹簧和阻尼器支承柱子端部绝对与相对位移时程曲线。由图7可知，无弹簧和阻尼器支承时，柱端C最大位移为282 mm，端部C与端部D的相对位移为54 mm;而有弹簧和阻尼器支承时，柱端C的最大位移为198 mm，较之前减少了29.8%，两端相对位移为45 mm，较之前减少了16.8%。总的来说，合理地设置弹簧和阻尼器可以有效地减小柱子在地震作用下的绝对位移和相对位移，从而达到减震、隔振的效果。

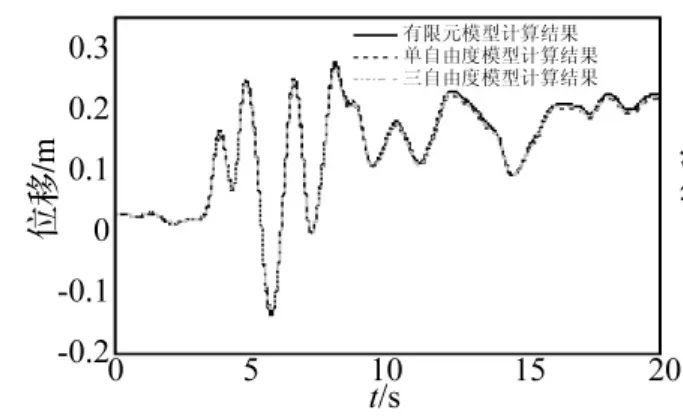
图6 跨中绝对位移时程曲线Fig.6 Absolute displacement-time histories in the mid-span of beam

图7 有无弹簧和阻尼器支承的位移时程曲线Fig.7 Displacement-time histories with and without supports of spring and dampers

1.3.2 轴力对弹簧和阻尼器支承柱子隔震效果的影响

由于受到上部覆土和结构自重的作用，地铁车站中柱端部会承受较大的轴力作用，其轴压比可达到0.5，甚至更高，因此在结构动力分析中必须考虑地震荷载与重力的耦合作用。本文采用理论分析模型分别分析大开地铁车站中柱端部无轴力作用与端部承受5000 kN的轴力作用时柱子在地震作用下的动力响应，计算时弹簧刚度k=20000 N/m，阻尼系数c=10000 Ns/m。柱端变位为零时跨中振动位移时程曲线如图8所示。

由式(1)可知，t时刻距柱底 x处的绝对位移y(x，t)由柱底、柱顶位移所引起的该处位移{y底(t)+［y顶(t)－y底(t)］x/l}和端部变位为零时该处的振动位移(yr(x，t))两部分组成。由图8可知，无轴力时yr(x，t)的最大值为2.7×10－5m，有轴力时其最大值为1.3×10－5m，减少了51.9%，说明在柱子振动的过程中，轴力给中柱提供了一定的约束作用，但并不代表轴力对柱子振动的影响是有利的，此类高轴压比构件延性往往较差，一旦地铁车站结构在剪切波的影响下顶板与侧墙交叉部位形成塑性铰，此时上部覆土及结构自重完全由中柱承担，轴力往往会加剧结构构件的破坏，因此，上部覆土及结构自重在地下结构动力分析中必须考虑。

1.3.3 弹簧和阻尼器参数的影响

为了研究弹簧刚度与阻尼系数对构件动力响应的影响，引入两个无量纲参数:端点最大位移比(ym)和跨中最大位移比(yc)。ym定义为设置弹簧和阻尼器支承时端点C位移的最大值yam与无弹簧和阻尼器支承构件在同样动载荷作用时端点C最大位移ybm之比，即ym=yam/ybm。yc定义为弹簧和阻尼器支承构件跨中相对于端点的位移的最大值yrm与无弹簧和阻尼器支承构件在同样动载荷作用时跨中最大位移ysm之比，即yc=yrm/ysm。

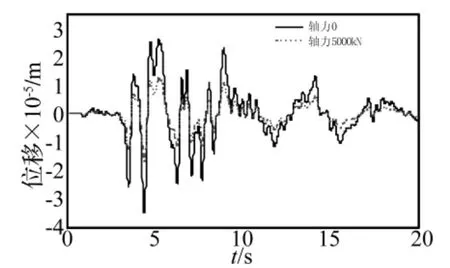
图8 柱端变位为零时跨中振动位移时程曲线Fig.8 Displacement-time histories in the mid-span with zero displacement at the ends

图9 端点最大位移比ym与弹簧刚度k和阻尼系数c的关系Fig.9 The relationship between ymand k，c

图10 跨中最大位移比yc与弹簧刚度k和阻尼系数c的关系Fig.10 The relationship between ycand k，c

端点A和端点B的地震输入荷载与上述算例相同。图9是端点最大位移比(ym)与弹簧刚度(k)和阻尼系数(c)的关系图。图10是跨中最大位移比(yc)与弹簧刚度(k)和阻尼系数(c)的关系图。由图9可见，随着弹簧刚度的增大，ym先增大后减小;当弹簧刚度较小时，ym随着阻尼系数的增大而增大;当弹簧刚度较大时，ym随着阻尼系数的增大而减小。由图10可见，随着弹簧刚度的增大，跨中最大相对位移比不断增大;当弹簧刚度不变时，随着阻尼系数的增大yc先减小再增大;当阻尼系数不变时，yc随着弹簧刚度的增大而增大，增长呈非线性增长。由此可见，设置弹簧阻尼器虽然可以有效的提高构件的抗震能力，但弹簧刚度与阻尼系数必须慎重选取，若弹簧刚度与阻尼系数选取不合理反而会增大构件端部的绝对位移与相对位移，设置弹簧和阻尼器减小结构构件相对位移的同时也可能会增大构件端部的绝对位移。

2 提高地铁车站结构抗震抗力的三维非线性性分析

为了进一步验证在非线性条件下端部弹簧与阻尼器支承提高地铁车站结构抗震能力的有效性，本文采用ABAQUS有限元软件，以大开地铁车站为背景，分别分析了中柱端部设置隔震支座和未设置隔震支座的地铁车站结构在地震作用下的动力响应。大开地铁车站主体结构主要有三种断面类型，其中破坏最为严重的断面形式如图11，该断面的车站结构埋深为4.8 m。

2.1 三维有限元模型的建立

土与结构整体有限元模型见图12(a)，未设置隔震支座柱子的有限元模型示意图见图12(b)，设置隔震支座柱子的有限元模型示意图见图12(c)，三维隔震支座在ABAQUS中通过弹簧和阻尼元件来实现。车站钢筋混凝土结构均采用钢筋和混凝土分离的方法建立三维模型，模型在纵向方向上取3.5 m。侧墙的厚度为0.70 m，配筋率为0.8%;顶板和底板的厚度分别为0.80 m和0.85 m，平均配筋率为1.0%;中柱的截面规格为0.40 m ×1.00 m，配筋率为6.0%。土体计算宽度取46 m，基岩面选在地下22.2 m处，土体的边界采用人工粘弹性边界［6］。，粘弹性边界相当于在边界上设置一系列由线性弹簧和粘滞阻尼器并联组成的物理元件。边界处输入阪神地震的实测地震加速度，地震动输入采用文献［6］中介绍的波场分解法，即将总波场分解为散射波场和自由波场，将任意外源波场统一为自由波场，在计算区域的边界上，由粘弹性边界吸收散射波场的能量，而自由波场直接转换为应力边界条件施加在边界上。入射波采用阪神地震的实测地震加速度，详见图13，详见图13，计算时同时考虑重力场与地震动场、水平地震动与竖向地震动的耦合作用，并采用接触面算法［7］模拟土与地下结构在接触面处发生大变形或发生相对滑动、分离等强动力接触非线性问题。土体模型选用扩展的D－P模型［7］，各计算参数取值如下:密度为1900 kg/m3，杨氏模量为180 MPa，膨胀角为20°，摩擦角为40°，泊松比为0.3;混凝土模型选用损伤塑性模型［8－9］，各计算参数取值如下:密度为2400 kg/m3，杨氏模量为32500 MPa，泊松比为0.2，初始压缩屈服应力为11.38 MPa，最大压缩屈服应力为24.0 MPa，最终压缩屈服应力为25.6 MPa，拉伸破坏应力为2.0 MPa。钢筋采用Mises弹塑性模型，各计算参数取值如下:弹性模量为200000 MPa，密度为7800 kg/m3，泊松比为0.3，初始屈服应力为 534 MPa、最大压缩屈服应力为745 MPa，最大屈服应力时的应变为0.3。根据［1］，隔震器的水平等效刚度取1055 kN/m，水平等效阻尼比取0.204，竖向等效刚度取 9060 kN/m，竖向等效阻尼比取0.1814。

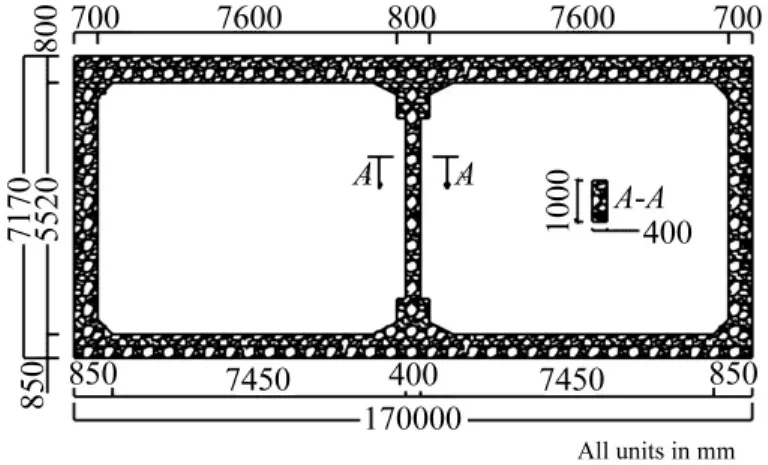
图11 大开地铁车站典型横断面图Fig.11 Sectional configuration of Dakai subway station

图12 有限元模型Fig.12 Finite element models

2.2 未设置弹簧和阻尼器与设置弹簧和阻尼器车站结构及中柱的破坏形态对比

图13 加速度时程曲线Fig.13 Acceleration-time histories

图14和～图15分别是柱子端部未设置隔震支座和设置隔震支座时结构断面20 s时的等效塑性应变图。由图14可知，未设置隔震支座情况下，随着侧墙与顶板交叉部位竖向承载能力的降低，顶板上覆土的大部分重量转移到由中柱承担，在由顶板破坏后传来的上覆土重力和地震动在中柱中引起的动压应力的共同作用下，中柱最终发生压曲和弯曲的破坏，导致中柱倒塌，进而导致车站顶板的塌陷，这与阪神地震中的实际破坏情况(见图1)基本一致。由图15可知，设置隔震支座情况下顶板、墙体、柱子均没有发生严重的变形，柱子的损伤破坏程度明显小于未设置隔震支座情况。

图14 20 s时刻结构的变形和等效塑性应变(未设置隔震支座)Fig.14 Distortion and equivalent plasticity strain of the structure at the time of 20 s(without isolator)

图15 20 s时刻结构的变形和等效塑性应变(设置隔震支座)Fig.15 Distortion and equivalent plasticity strain of the structure at the time of 20 s(with isolator)

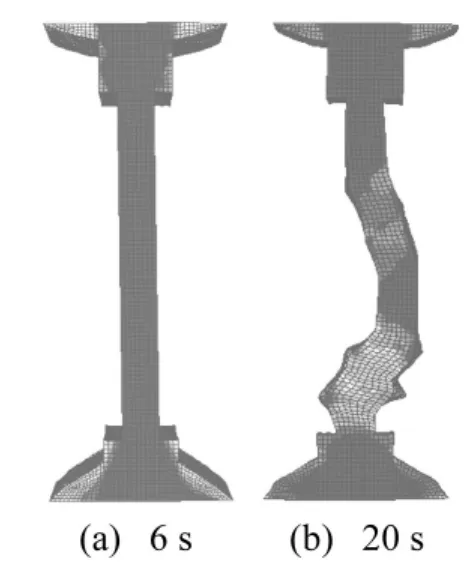
图16 中柱的变形和等效塑性应变(未设置隔震支座)Fig.16 Distortion and equivalent plasticity strain of the column(without isolator)

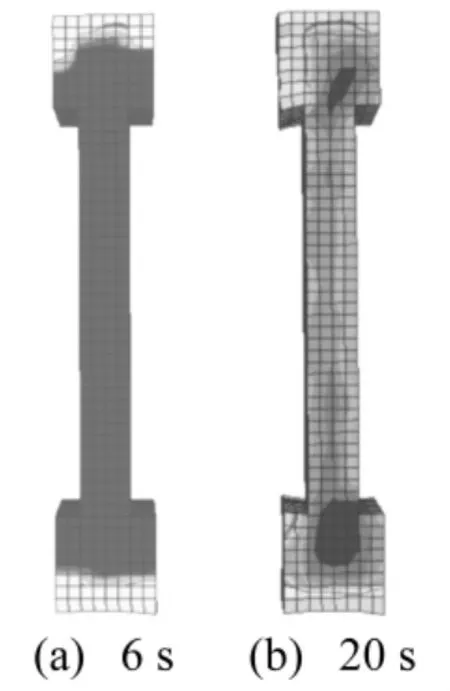
图17 中柱变形和等效塑性应变(设置隔震支座)Fig.17 Distortion and equivalent plasticity strain of the column(with isolator)

图16和图17分别是未设置隔震支座和设置隔震支座情况下柱子在不同时刻的变形及等效塑性应变发展情况。由图16可知，未设置隔震支座情况下，在6 s左右柱子的端部产生了较为明显的塑性变形，随着时间的增长，底部的塑性变形越来越大，20 s时柱子中混凝土的等效塑性应变最大值达到了0.724，钢筋的等效塑性应变最大值为0.433，实际上已被拉断。由图17可知，设置隔震支座情况下，在6 s左右整个中柱仅发生了一些轻微的塑性变形，随着时间的增长，柱子的塑性变形虽然逐渐变大，但没有达到破坏，20 s时柱子的等效塑性应变最大值仅为0.098，钢筋远未达到拉断状态，较未设置隔震支座情况下有明显的减小。

综上所述，在柱子端部设置隔震支座可以有效减小柱子的变形及破坏。

3 结论

本文基于第二类拉格朗日方程，建立了地震荷载和轴力联合作用下柔性动边界梁动力响应的分析方法，分别分析了轴力、弹簧刚度与阻尼系数对动力响应的影响特点与规律，并进一步利用有限元软件ABAQUS对阪神地震中大开地铁车站结构中柱端部在有无设置三维隔震支座分别进行了非线性数值分析，主要结论有:

(1)与有限元数值计算结果对比表明，文中所提出的分析方法可以较好地分析地震荷载与轴力联合作用下柔性动边界梁的动力响应问题;

(2)在强震荷载作用下，在地铁车站中柱的端部合理设置隔震支座能够有效减小结构(尤其是柱子)的变形与损伤破坏，从而提高其抗震能力;

(3)柱子上部覆土及自身重量产生的轴力会对柱子的振动响应产生影响，此类构件延性较差，一旦结构交叉部位产生塑性铰，上部覆土及结构自重会加剧中柱的破坏。

［1］王曙光.高层建筑隔震设计方法研究与应用及装置产业化开发［R］.南京工业大学，2008.

［2］方 秦，杜茂林.爆炸荷载作用下弹性与阻尼支承梁的动力响应［J］.力学与实践，2006，28(2):53－56.

［3］方 秦，陈 力，杜茂林.端部设置弹簧和阻尼器提高防护门抗力的理论与数值分析［J］.工程力学，2008，25(3):194－199.

［4］宋春明，王明洋，唐正国.柔性动边界梁在横向撞击下的动力响应［J］.解放军理工大学学报，2008;9(2):151－155.

［5］宋春明，王明洋，王德荣.爆炸荷载作用下柔性动边界拱的动力响应分析［J］.兵工学报，2008，29(7):813－818.

［6］赵建锋.考虑土－结构动力相互作用和多点输入的桥梁非线性地震响应分析［D］.北京:北京工业大学，2007.

［7］Analysis user’s manual of ABAQUS 6.6 Volume Ⅲ:Materials［P］.American:ABAQUS Inc.，2007.

［8］方 秦，还 毅，张亚栋，等.ABAQUS混凝土损伤塑性模型的静力性能分析［J］.解放军理工大学学报，2007，8(3):254－260.

［9］Huan Yi，Fang Qin，Chen Li，et al.Evaluation of Blast-resistant Performances Predicted by the Damaged Plasticity Model for Concrete［J］.Transactions of Tianjin University，2008，14(6):414－421.