多源激励作用下结构振动响应的试验研究

王雪仁，缪旭弘，贾 地，叶文荣

(1.海军装备研究院 舰船所，北京 100161;2.92854部队，湛江 524000)

近年来，人们对多点激励问题的关注主要来源于对船舶、飞机等复杂结构振动噪声特性控制的需求。这些复杂结构内部机械设备较多，种类各不相同，且往往同时运行工作，导致其结构的振动响应实际是多个机械设备振源共同作用的结果。目前，多点激励结构振动响应的数值仿真计算方法主要有谐响应法、谱分析法和时域法，但这些方法均是基于线性的分析方法，不能考虑激励源之间的耦合作用和非线性响应。为考察结构在多点激励下的真实振动响应特性，须借助于试验分析方法。圆柱壳体结构是船舶、飞机等复杂结构的基本组成部分，虽然对其开展的理论和试验研究比较多，但多集中在光圆柱壳、舱段结构在单激励作用下的振动响应分析［1－4］，关于更复杂结构和多点激励力作用下的结构振动响应则较少见。

本文是开展多点激励条件下结构的振动响应试验研究，发展相应的测量方法，并初步分析频率、相位等因素对不同圆柱壳结构在多个振动源激励条件下的振动响应特性。

1 多点激励振动响应理论基础

阻尼系统的结构有限元动力学方程为［5］:

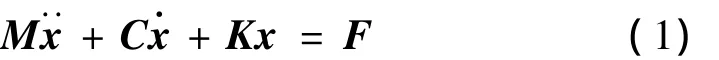
对式(1)进行拉式变换可得:

式中，Z(s)为系统的阻抗矩阵，其逆矩阵即为系统的导纳矩阵或传递函数矩阵H(s):

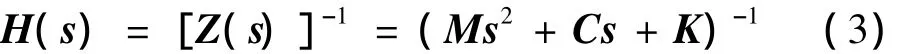
将式(3)中的s用jω代替，即可得到系统的频响函数H(ω)为:

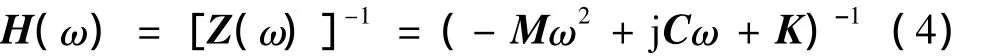
将式(4)代入式(2)即可得到系统的输入输出及频响函数的关系为:

因此，系统在激励力向量F(ω)作用下各点的振动位移响应输Xi(ω)为:

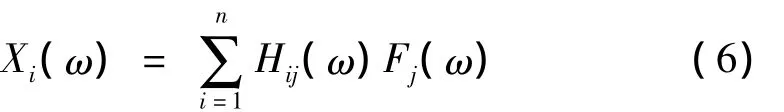
式中，i代表振动响应测量点，j代表激励点，Fj(ω)表示激励点j处的激振力。

式(6)即为试验中获得多源激励条件下结构振动响应结果的基本公式。

2 结构模型

考察的模型为图1和图2所示的圆柱壳体结构。图1为径向简支光圆柱壳结构，由普通碳钢加工制成，壳体厚6 mm。壳体的简支边界条件是通过将很薄的环形钢片(厚度约1 mm)用24个小螺钉(直径约3 mm)铆接在壳体上实现的。考虑到壳体的重量较大，为了保证足够的刚度，端盖与支架都选用厚度约35 mm的碳钢。端盖和支架是通过焊接在端盖上的轴(直径约36 mm)连接的。图2为自由边界轴系圆柱壳结构，材料仍为普通碳钢，壳体壁厚为5 mm，轴系为外径为32 mm，壁厚为5 mm的中空结构，轴承支撑面板的壁厚为4 mm，整个壳体由五个分段组成，分段之间靠内法兰或外法兰螺栓连接，在Ⅲ、Ⅵ、Ⅴ段内设计有轴系结构。

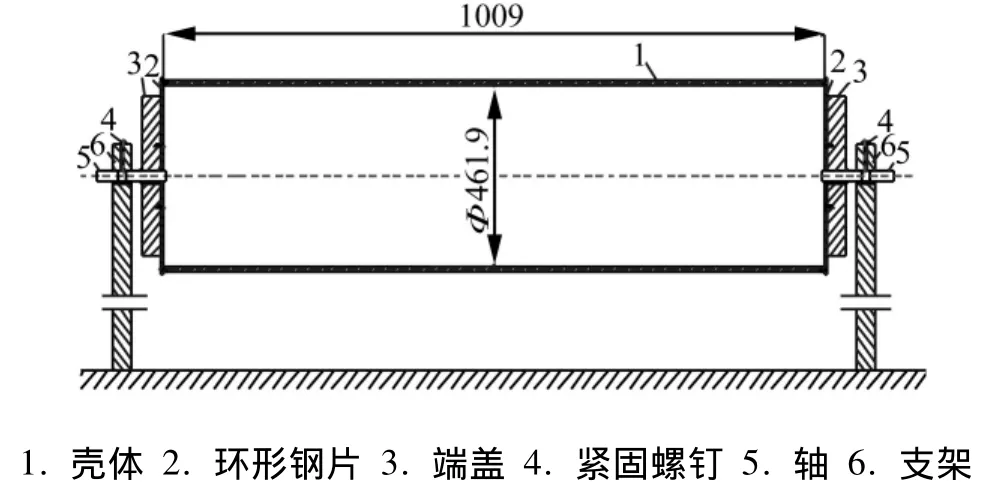
图1 光圆柱壳体模型结构和尺寸Fig.1 Structure and dimensions of the cylindrical shell model

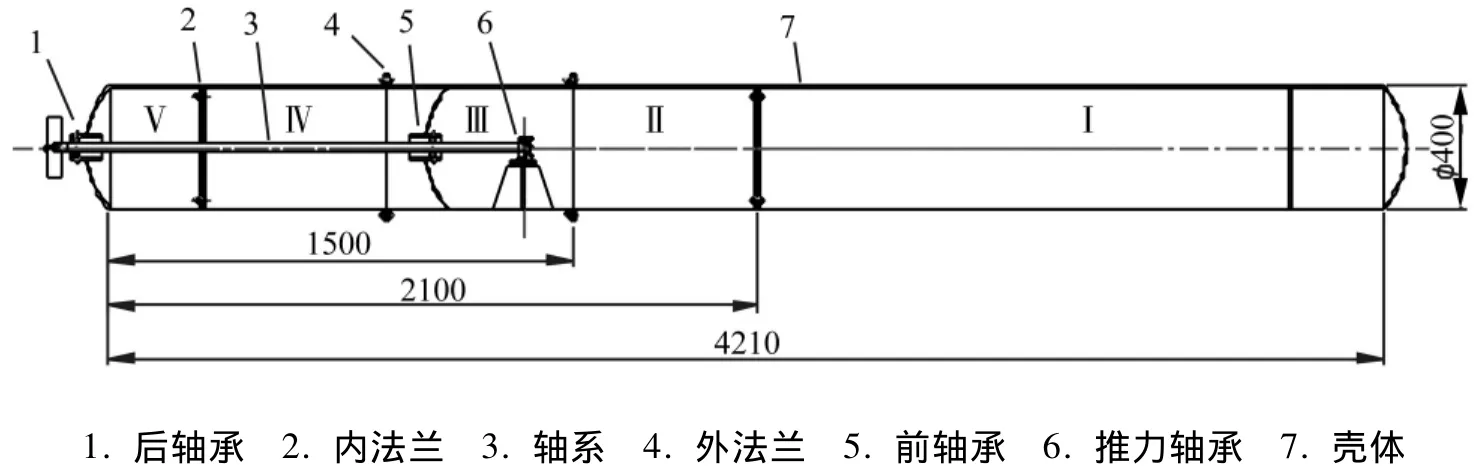
图2 轴系圆柱壳体模型结构和尺寸Fig.2 Structure and dimensions of the cylindrical shell model with a shaft

3 测量系统和方法

结构的振动特性测量方法包括两部分:模态测试和振动响应测试。模态测试主要用于模型和测量系统精度的考察，并进行修正和完善，为后续的振动响应测量奠定基础。模态测试和振动响应测试时，光圆柱壳结构为径向简支，轴系圆柱壳结构为弹簧吊装(悬挂系统的第一阶模态约为4.7 Hz)。

3.1 模态测试

试验中采用脉冲激励，为激起结构的中高频模态纵向、切向和径向响应，采用铝质力锤头，并沿这三个方向分别敲击测量。为考察1000 Hz以下结构的中低频振动特性，试验中模态的采样频率设置在2048 Hz以内。数据采集与处理系统采用LMS Test.lab系统。

为获得结构的振型，采用单点激励多点响应的测试方法。激励点的选择将根据仿真计算结果，确保其位置不在前三阶模态振型的节点处。为确保对模态振型的准确识别，响应测试点所测得的信息要求有尽可能高的信噪比，因此，测试点不应该靠近节点。但实际过程中模态节点的位置很难准确确定，为避免局部测试点在振型节点处，从而导致测试数据失效，试验中将根据计算结果，在保证测试量在可接受的范围内情况下，尽可能缩小测试点之间的距离，两个圆柱壳结构的模态测试响应测点布置如表1所示。测点的布置合理性通过模态之间的模态置信度(MAC)来评价。模态置信度表达式为［6］:

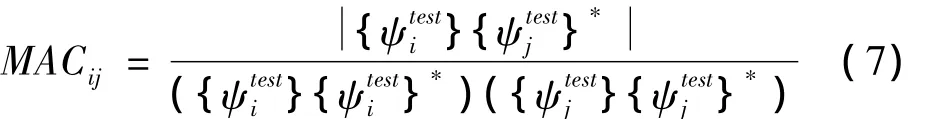
式中，MACij表示第i和第j阶试验模态的置信度，取值区间为［0，1］，ψtest表示试验模态的振型，* 表示矩阵转置。测点布置合理的情况下MAC矩阵的分布规律为主对角线元素为1，而其余值在0.1以下［5］。

表1 模态测试响应测点布置Tab.1 Response points on the two cylindrical structures for modal tests

3.2 振动响应测试

试验中激励源采用激振器模拟，激振器均处于自由悬挂状态，以模拟自由边界条件。激励点的选择如图3中a，a1，a2，a3和 b点，振动响应测量点的选择如图中1至10点。采用在a和b点，a1和b点，a2和b点或a3和b点两点同时激励来考察多点激励响应的情况，振动响应仍采用ICP三轴加速度传感器来测量各测点三个方向的加速度值。测试系统示意图如图4所示。图中a点激振器为1#激振器，在试验过程中其位置可在激励点a，a1，a2和a3点之间变换，b点为2#激振器，实验过程中其位置固定不变。试验的数据采集和处理设备采用Pulse系统，两个功率放大器均采用YE5872功率放大器。两激振力之间的相位由PULSE系统内的信号源来控制输出。

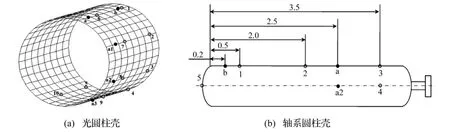
图3 试验中激励点与振动响应测量点的布置示意图Fig.3 Sketch map for the positions of exciting and response points in the experiment

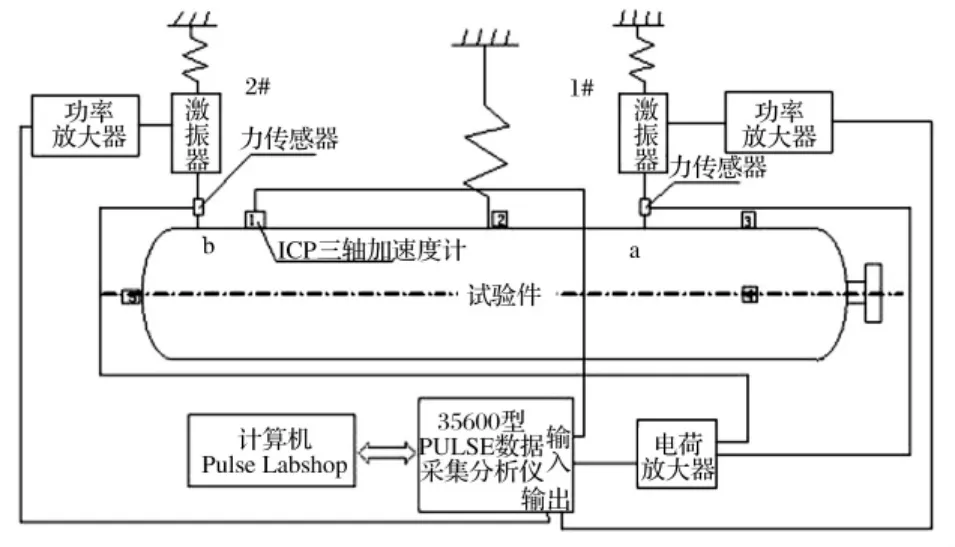
图4 测试系统示意图Fig.4 Sketch map for the testing equipments

4 测试结果分析

4.1 模态测试结果

图5为圆柱壳结构试验模态的MAC值，从图中可以看出，试验测得的各阶振型保持了较高的正交特性，非对角元素除轴系圆柱壳体的MAC24、MAC42、MAC89和MAC98达到30%左右，其余均较小，在0.1以下，说明传感器的布置是合适的。结构典型模态试验值与有限元仿真计算值比较如表2和3。可以看出，试验值与计算结果吻合很好，说明了模型和试验方法的正确性，可进一步进行振动响应测量分析。

图5 试验模态的模态置信度Fig.5 MAC among the testing modes

表2 光圆柱壳结构典型模态比较 单位:HzTab.2 Comparison of the typical modes of the simple cylindrical shell between different methods Hz

表3 轴系圆柱壳结构典型模态比较 单位:HzTab.3 Comparison of the typical modes of the cylindrical shell with a shaft between different methods Hz

4.2 振动响应测试结果

4.2.1 激励源之间的耦合关系

针对光圆柱壳结构，图6和图7为两力之间的相位差对不同频率、不同夹角时两激振器力杆上力传感器输出信号的影响关系曲线，相位差表示2#激振器输出信号滞后于1#激振器输出信号的时间。

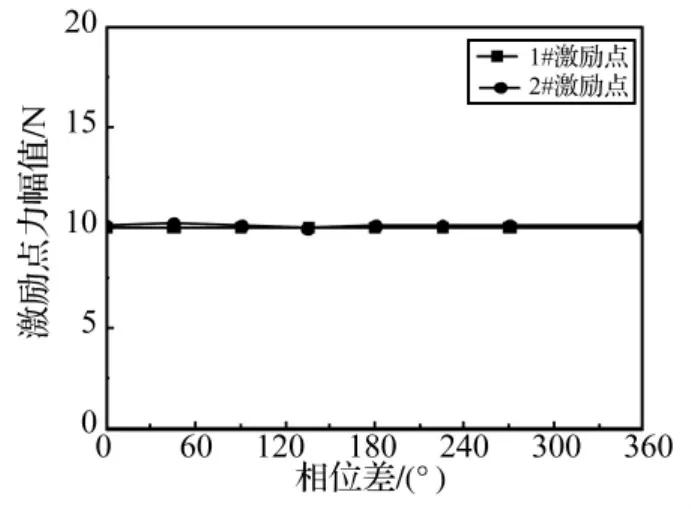
图6 两激励力均为300 Hz时耦合关系Fig.6 Coupling relationship between the two forces whose frequency is 300 Hz

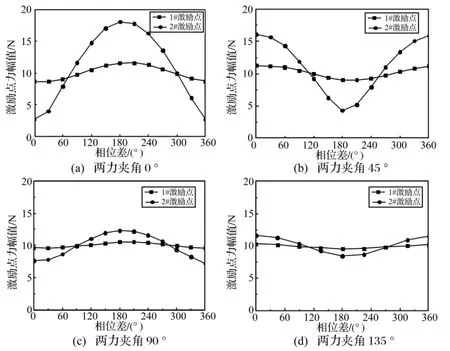
图7 两激励力均为500 Hz时耦合关系Fig.7 Coupling relationship between the two forces whose frequency is 500 Hz

从试验过程中得知，在300 Hz以下频段内两激振器上力传感器的输出信号并不随两激励力之间相位差和夹角的改变而改变，且均保持在10 N(初始施加载荷)，如图6所示。因此，300 Hz以下频段内两激励力之间不存在耦合影响关系，保持了较好的独立性。在300 Hz以上频段内两激振器上力传感器的输出信号随两激励力之间相位差和夹角的变化而变化较大，力的幅值随相位差近似程余弦变化，在0°或180°达到最大或最小，如图7所示。图8为两激励力之间的相干系数频谱曲线，可以看出，在300 Hz以下频段内相干系数基本在0.2以下，而300 Hz以上频段则接近于1。因此，300 Hz以上频段内两激励力之间存在严重的相互影响耦合关系，导致各激励力的性质相对于单独激励时发生变化。

出现上述现象的原因主要有以下两点:一方面可归结于光圆柱壳结构的模态主要集中在300 Hz以上频段，而在300 Hz以下频段内除结构的(1，3)阶模态外几乎不存在其它模态，如图9所示，由此导致结构在300 Hz以上频段的振动特性出现较强的非线性(主要是由结构的共振引起的);另一方面是由于在轴系圆柱壳试验测试过程中并未发现两激励力之间明显的相互影响现象(即使在其模态比较密集的200 Hz以上频段)，因此推测光圆柱壳上两激励力的位置较近也是导致激励力出现耦合现象的重要原因之一。

在试验过程中还发现，不同频率激励力之间并无明显的相互影响关系。因此，不同激励频率的激励力，即使倍频或谐频激励力之间均可视为独立的激励力，不用考虑相互之间的耦合关系。

4.2.2 结构的振动响应

在有限元中计算结构响应时，阻尼损耗因子的选择至关重要。结合模态测试数据，计算中的损耗因子选取为质量阻尼系数α=52.1，刚度阻尼系数β=5.96×10－6。

针对光圆柱壳结构，两个弱耦合单频激励力同时作用下结构的振动响应试验值和有限元预测结果比较如图10所示。可以看出，二者吻合很好，所发展的多点激励振动响应试验方法是合理的，有限元可正确预测弱耦合或非耦合激励源作用下的结构振动响应。

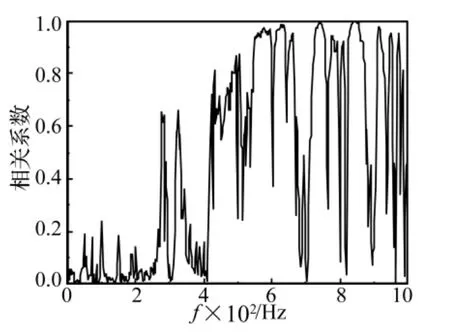
图8 两激振器同时垂向激振时激励力之间的相干系数Fig.8 Correlation of the two vertical forces

针对轴系圆柱壳结构，两点同时垂向随机激励(夹角为0°)时，激励源之间的相干系数如图11所示。可以看出除500 Hz以上个别频率下相干系数较大外，其它频率下相干系数均小于0.2，说明二力之间的相互影响很小，处于弱耦合状态，测得的激励源载荷数据可直接应用于数值仿真计算。结构各测点的振动响应加速度试验测量值与仿真计算值比较如图12。可以看出，二者变化趋势基本一致，特别是在300 Hz以上测量频段内吻合较好。引起仿真计算与试验结果误差的原因可归结为以下几点:一是实际结构在模态附近存在较强的非线性响应;二是试验中用于模拟模型自由边界条件的弹簧吊装方式对结构低频振动特性具有更明显的影响，导致300 Hz以下的误差增大;三是试验中不可能激起结构的所有模态，特别是结构的局部模态，导致相应的振动响应测试结果与计算结果误差增大。

图9 光圆柱壳的模态分布Fig.9 Mode distribution of the simple cylindrical shell

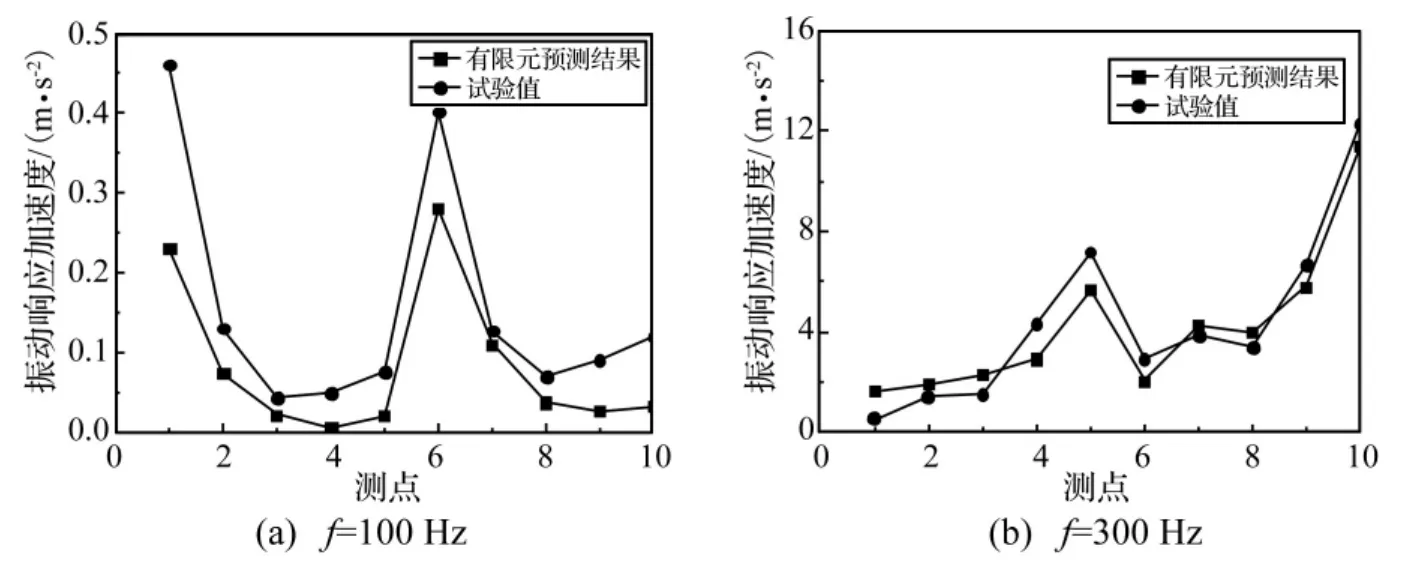
图10 结构振动响应结果比较Fig.10 Comparison of the structure vibration response

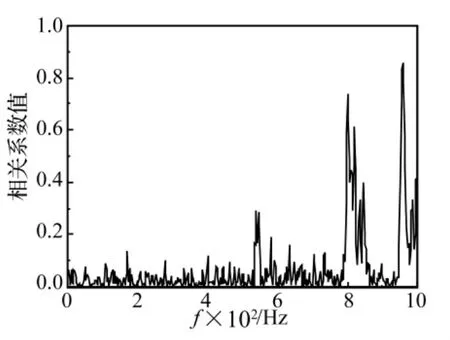
图11 两力夹角为0°时激励力之间的相干系数频谱曲线Fig.11 Correlation of the two forces between which the direction angle is 0 degree

4.2.3 相位的影响

两激振器以相同频率同时激振时，结构的振动响应频率以激振频率为主，其它响应频率(包括激振频率的谐频)对应的振动量值相对很小，可忽略不计。两激振器同时垂向激振时，激励力之间的相位差对各测点振动响应的影响如图13所示。可以看出，激励力之间的相位差对振动响应的影响较大，二者近似呈余弦的变化关系，振动响应在激励力之间的相位差为0°或180°时达到最大或最小。

5 结论

开展了多点激励结构动力学模型试验，考察了多个激励源之间的耦合关系，以及多源激励条件下结构的振动响应规律，主要结论如下:

(1)实验结果与数值仿真计算结果对比分析表明试验方法合理，测试系统可靠，所得数据可信;

(2)激励源之间的耦合关系由模型尺寸、模态密度、激励频率、激励力大小等多种因素决定，因此，激励源之间耦合关系的强度判别需综合考虑这些因素;

(3)相位对多点激励下结构的振动响应具有明显的影响，为精确考察多源激励条件下结构的振动响应，相位因素不可忽略，但将激励力幅值应用于仿真计算时，可得到保守的预测结果;

(4)激励源之间存在弱耦合或不相关时，试验测得的激励源载荷数据可直接应用于数值仿真计算的边界条件输入，但存在耦合关系时，则必须进行解耦后才能作为仿真计算的激励边界条件。

图12 两激振器同时垂向激励时试验测量结果与仿真计算结果比较Fig.12 Comparison of the structure vibration response between the measurements and predictions when the two vibration exciters are in a vertical direction

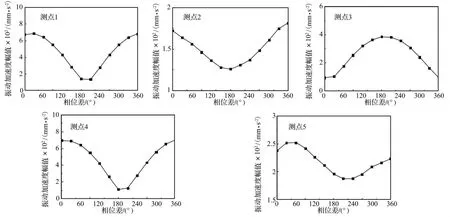
图13 两点激振频率均为300 Hz时相位差对响应频率为300 Hz振动加速度的影响Fig.13 Influence of the phase difference on the vibration response at 300 Hz when the frequencies of the two force are 300 Hz

［1］孟宪举，张 策，卿光辉.加筋圆柱壳的振动特性分析［J］.振动工程学报，2005，18(1):36－40.

［2］俞孟萨，吴永兴，吕世金.加肋圆柱壳声学相似性试验［J］.中国造船，2002，43(2):50－57.

［3］吴文伟，吴崇健，沈顺根.双层加肋圆柱壳振动和声辐射研究［J］.船舶力学，2002，6(1):44－51.

［4］姚熊亮，刘庆杰，翁 强，等.水下加筋圆柱壳体的振动与近场声辐射研究［J］.中国舰船研究，2006，1(2):13－19.

［5］殷学纲，陈 淮，蹇开林编著.结构振动分析的子结构方法［M］.北京:中国铁道出版社，1991.

［6］傅志方，华宏星编著.模态分析理论与应用［M］.上海:上海交通大学出版社，上海，2000.