气动隔振系统非线性特性仿真与数值分析

钟艳春，杨庆俊，包 钢

(哈尔滨工业大学 机电工程学院，哈尔滨 150001)

气动隔振系统承载力大、有效行程大、隔振效果优异，广泛应用在仪器平台、光学平台、精密加工与检测、舰船动力设备隔振、车辆悬挂等的振动隔离［1－4］。由于非线性微分动力系统的复杂性，空气弹簧的弹性恢复力非线性对隔振系统特性的影响没有同时得到适当的研究，绝大多数的设计、研究都以隔振系统工作在微幅振动的条件下进行线性化，气动被动隔振系统常被简化为由空气弹簧的弹性、阻尼器的阻尼以及被隔载荷的质量形成的弹簧－阻尼－质量系统，大振幅条件下空气弹簧非线性的影响则简化为弹簧刚度系数和自振频率的变化［5－6］。在主动控制中，大多也沿用这种线性模型［7］。这样的处理对于处于微幅振动的系统来说是适当的，但是对于大振动幅度的应用，线性模型不再有效。在Koyanagi等［8］的研究中指出车辆空气悬架振动隔离具有较强的非线性，不仅使精确设计隔振特性十分困难，而且是引起车辆连续横滚的主要原因。

近年来逐渐有学者开始了气动隔振系统的非线性研究，Philips公司的 Marcel Heertjes［9］研究了气体压缩的非线性对传递率和导纳的影响。陈帅，温金鹏等［10－11］应用能量方程，运动学方程、理想气体方程，建立了弹性织布气囊的缓冲动力学模型。方瑞华［12］将气体压缩性的非线性按泰勒展开为三次多项式后，求解了其二倍频响应，并在模型试验中清楚地发现了倍频响应和零偏。尹万建［13］用3次多项式拟合膜式空气弹簧的实测弹性非线性，研究汽车空气弹簧悬架的非线性动力学行为，发现了倍频、分频等非线性现象，以及这些现象与非线性弹性多项式的系数的关系 。然而，这些研究都将气动隔振系统的非线性表示成多项式的形式，这可能和实际的模型有一定差别，本文从基本的方程入手，对气动隔振系统非线性特性进行了仿真与数值分析。

1 系统模型

系统模型建立

为了方便起见，本文选用简单的单腔气弹簧对其进行非线性特性分析，其物理模型简单表示如图1。

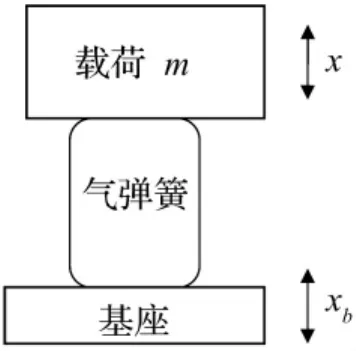
图1 气动隔振系统模型简图Fig.1 Schematic diagram of the neumatic vibration isolation system

本文将气弹簧的机械弹簧刚度(如波纹管式气弹簧中波纹管的纵向刚度、囊式气弹簧橡胶及帘线形成的纵向刚度等)单独列出，并设为k，内阻尼系数为c(设为线性粘性阻尼力)，则载荷运动动力学方程为:

式中:p为气腔内压力，p0为大气压力，A为气体有效作用面积，m为载荷质量，x为载荷振动，xb为基座振动。

设腔内空气为理想状态气体，其气体状态方程为:

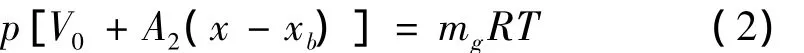
式中:V0为气弹簧初始容积，A2为气弹簧容积面积，mg为气腔内气体质量，R为空气气体常数，T为腔内气体温度。

气体热力学方程:

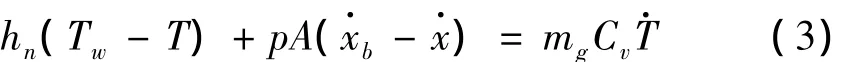
式中，hn为筒壁与腔内气体之间热交换系数，Tw为筒壁温度，Cv为空气比热。

筒壁热力学方程:

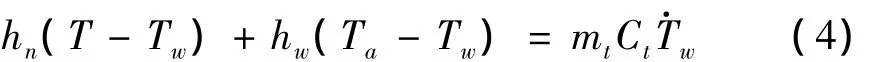
式中，hw为筒壁与腔外气体之间热交换系数，Ta为腔外气体温度，mt为筒壁质量，Ct为筒壁比热。

2 系统简谐激励频谱分析

以上动态方程可以看出，这是一个具有一定非线性的系统。根据以上各方程，利用Matlab软件对模型进行了仿真分析，仿真结果对于以后的数学分析及实验具有很好的指导意义。各参量选取如表1所示。

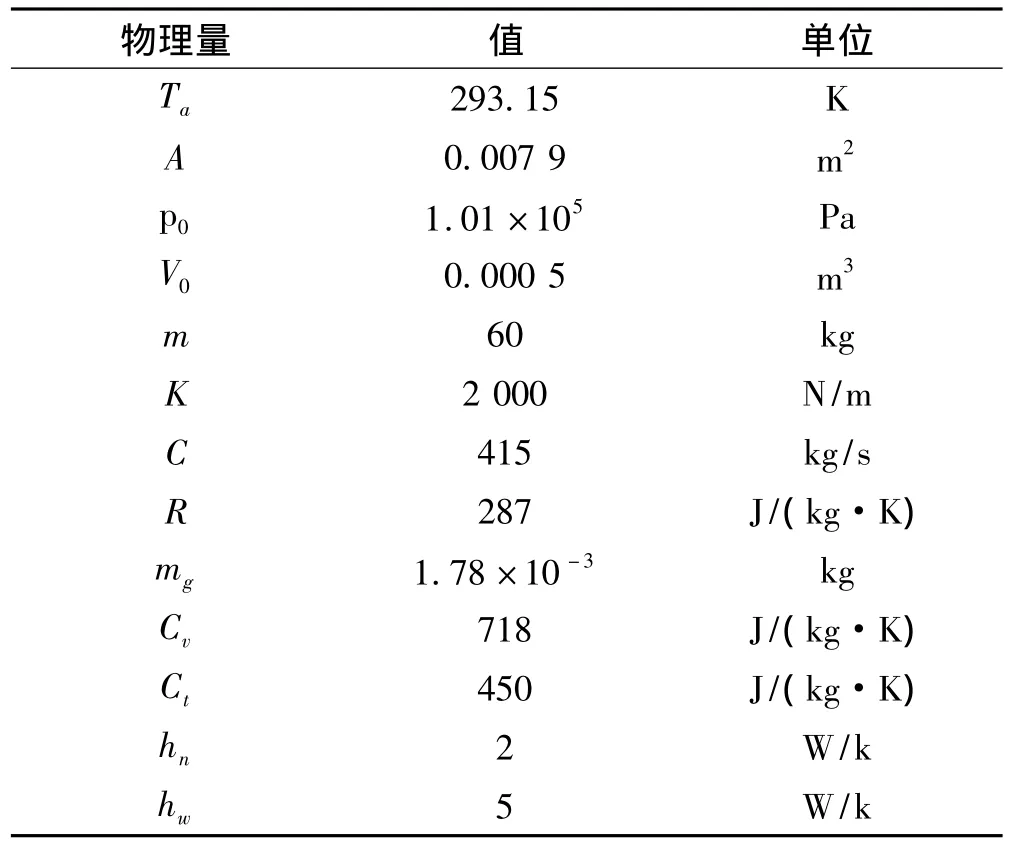
表1 算例系统计算参数Tab.1 Parameters of example vibration isolation system

仿真模型中激励幅度为0.025 m，初始压力为0.3 MPa，仿真时间取1500 s，此时系统已处于稳态。激励频率 ω'依次选 1 rad/s，10 rad/s，20 rad/s，50 rad/s，100 rad/s，300 rad/s。其响应频谱依次如图2(a～f)所示。

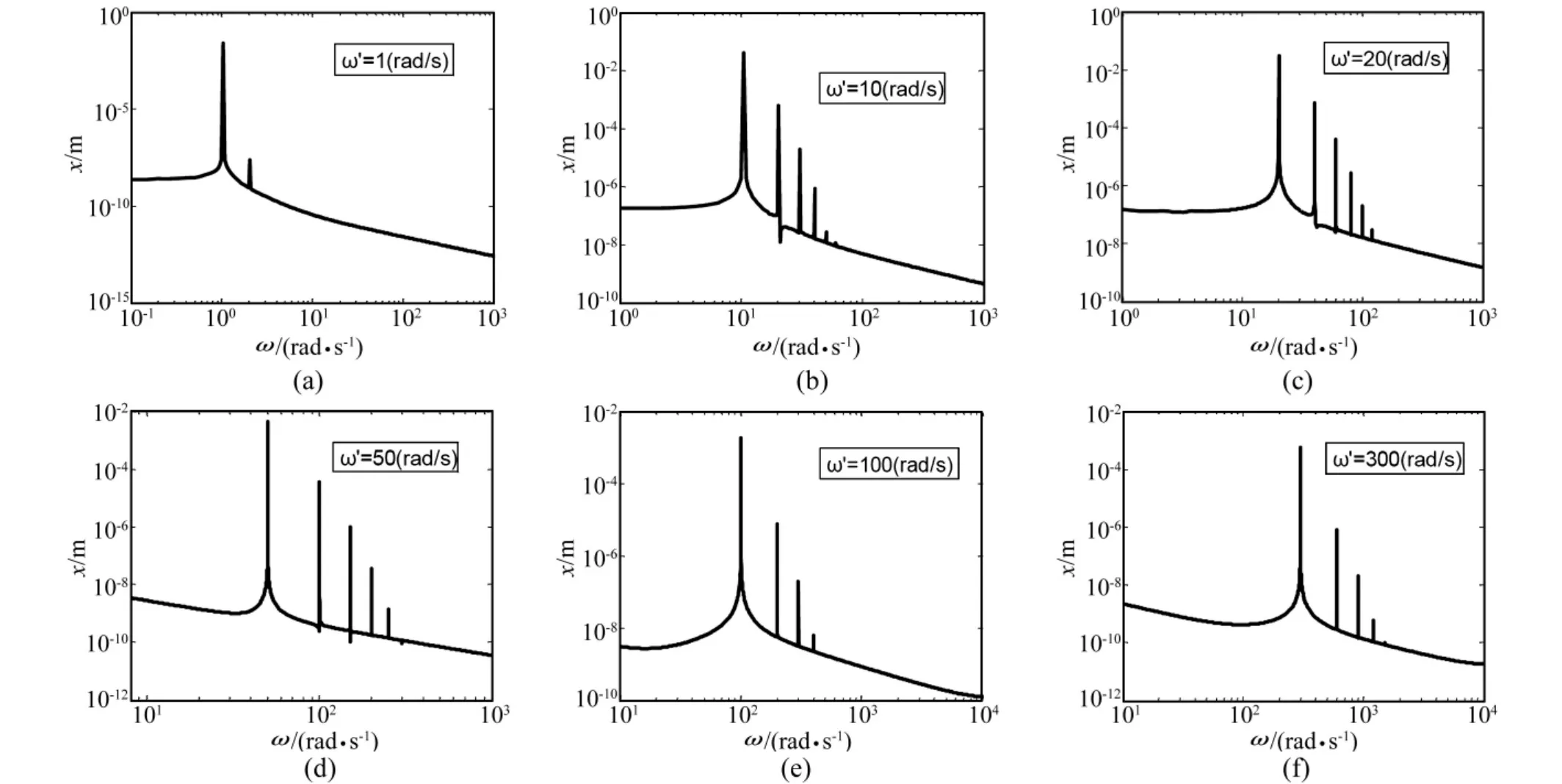
图2 不同激励频率响应幅值谱Fig.2 Amplitude spectrum under different excited vibration frequency

从以上各图中分析可以看出:单频激励会诱发高次谐波，且具有较高的幅度。高次谐波的幅度随激励频率的变化而变化:当激励频率很低时，高次谐波幅度小，激励频率越低，高次谐波越小(如图2a，b);当激励频率很高时，高次谐波幅度小，激励频率越高，高次谐波越小(如图2e，f);激励频率为中间频率，即系统线性化固有频率附近时，高次谐波严重，甚至要5、6次谐波才衰减到主峰的1%以下(如图2c，d)。

由于系统的非线性，导致振动中心点偏移，为了解偏移的规律性，图3列出了在不同激励幅值下系统零频偏移随频率变化的曲线。激励幅度取值范围为:0.0025 m ～0.06 m。

从图3中可以看出，零频偏移随频率变化明显，低频和高频时，零频偏移很小，中频段零频偏移大;其值也随激励幅度变化而变化，激励幅值越大，零频偏移越大。图4为不同激励幅度下，系统基频振幅随频率变化响应曲线。

从图4可以看出，系统在低频时，非线性特性不明显，基频响应跟随激励幅值，中频段非线性现象明显，尤其在共振频率14 rad/s附近，基频响应峰值很高，在高频段系统隔振效果比较好，幅值衰减得很快。

不同激励幅度下，基频能量占系统总能量的比值见图5所示。

从图5中可以看出，系统在低频和高频段，基频能量占系统总能量的比值接近1，在中频段能量分布比较分散，共振频率14 rad/s附近，激励幅值为0.06 mm时，基频能量占系统总能量的比值为0.98。不同激励幅度下，系统的一倍频幅值响应曲线如图6所示。

图3 零频偏移曲线Fig.3 Displacement at zero frequency

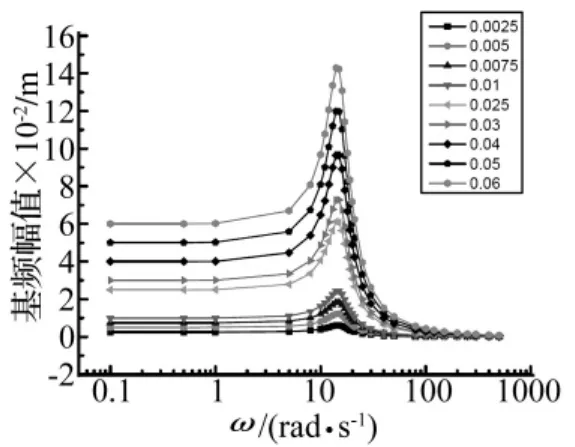
图4 基频幅值响应曲线Fig.4 Amplitude response at fundamental frequency

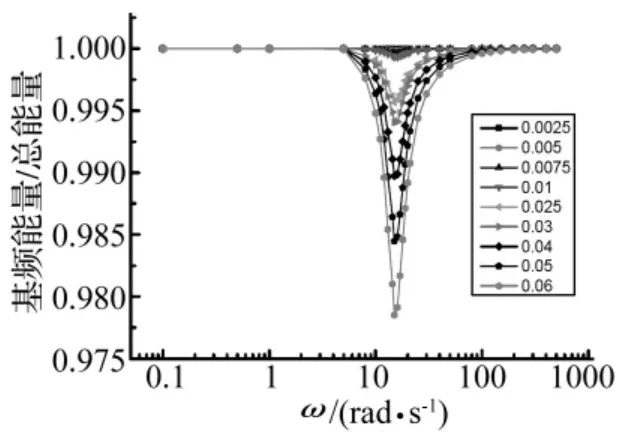
图5 基频能量曲线Fig.5 Energy at fundamental frequency

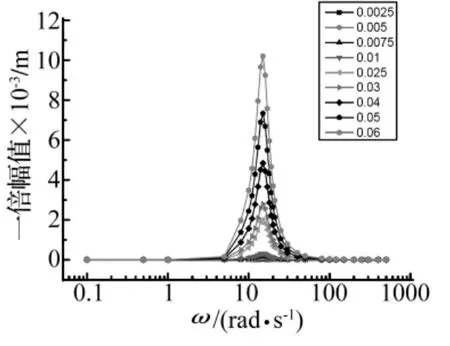
图6 一倍频幅值响应曲线Fig.6 Amplitude response at one octave

和基频幅值响应不同，在低频时，系统一倍频响应小。在系统线性化固有频率14 rad/s附近，激励幅值为0.06 mm 时，共振峰达到 0.01 m。

不同激励幅度下，一倍频能量占系统总能量的比值见图7所示。

一倍频能量占系统总能量在系统线性化固有频率14 rad/s附近达到最大值，激励幅值为0.06 mm时，比值为0.005，并且随激励幅值的增大而变大。

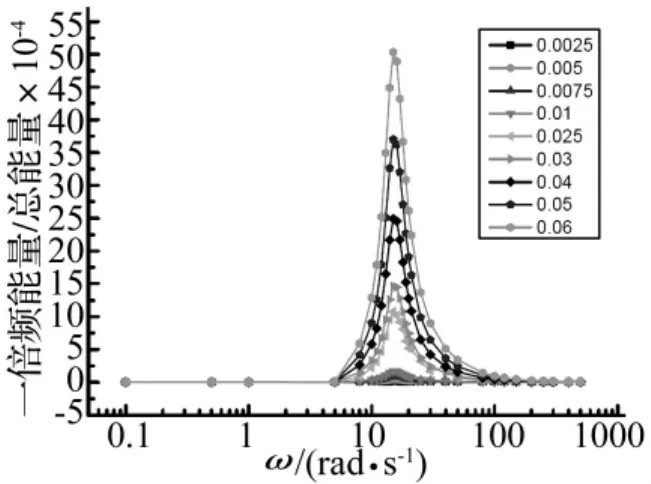
图7 一倍频能量曲线Fig.7 Energy at one octave

3 数值计算

假设基座的运动为:

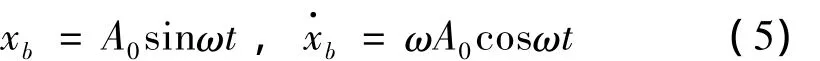
对载荷响应的频谱分析表明，稳态解中除激励频率成分外，还包含有零频分量，即偏移、包含有1/2分频、包含倍频、包含3/2、5/2等频率成分。以该仿真结果为指引，假设系统的状态变量p、x、Tw和T均包含零频分量和1/2分频及其各次倍数分量，即:

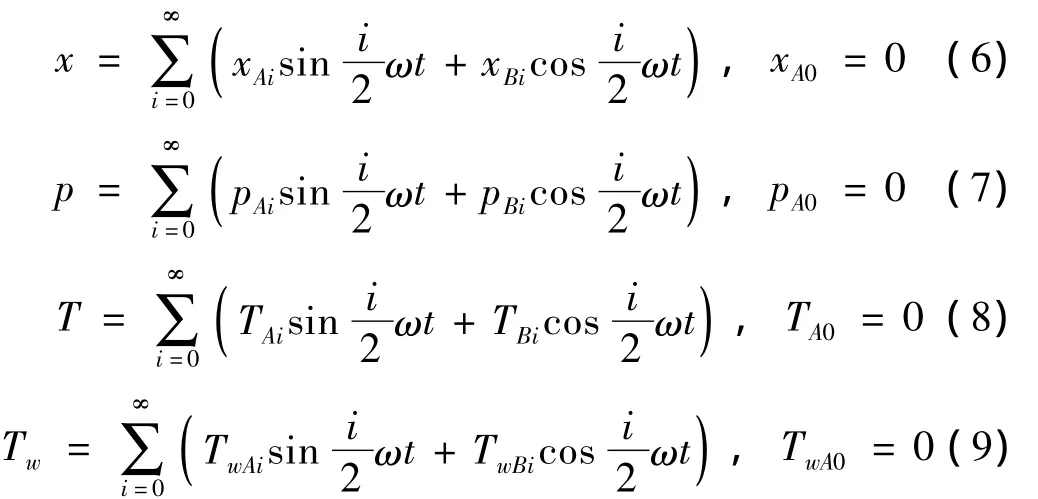
将式(5)～式(7)代入方程(1)，得:

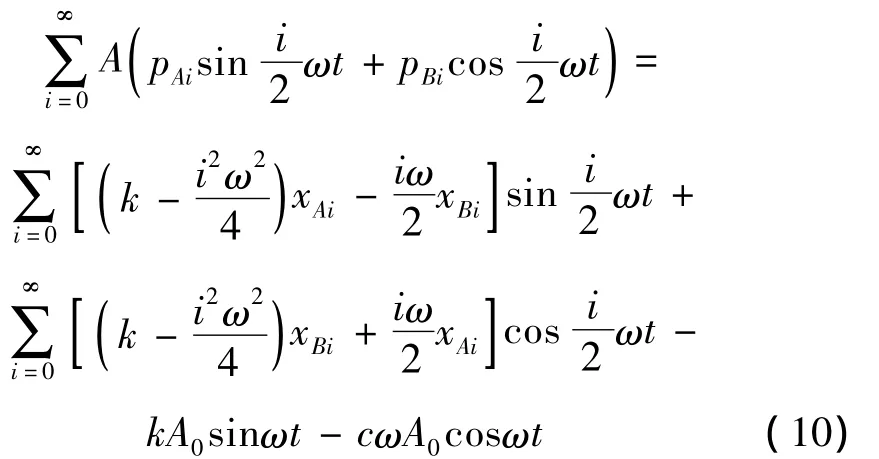
该方程为线性方程，令对应项系数相等，可得:

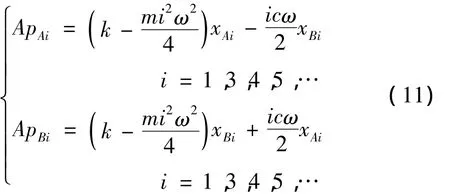
特别地，当i=0时有:

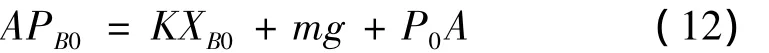
当i=2时有:

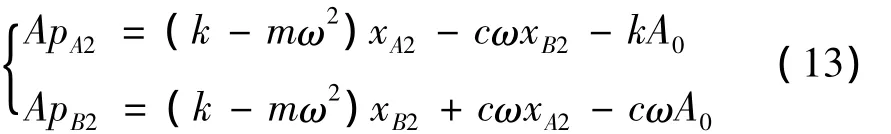
将式(5)～式(8)代入方程(2)，得:

为方便起见，将V0合并到XB0中并仍记为XB0，将－A0合并到 XA2中并仍记为XA2。将左边交叉相乘，将以上各项中的系数合并，并令其等于方程右端对应项系数，则:

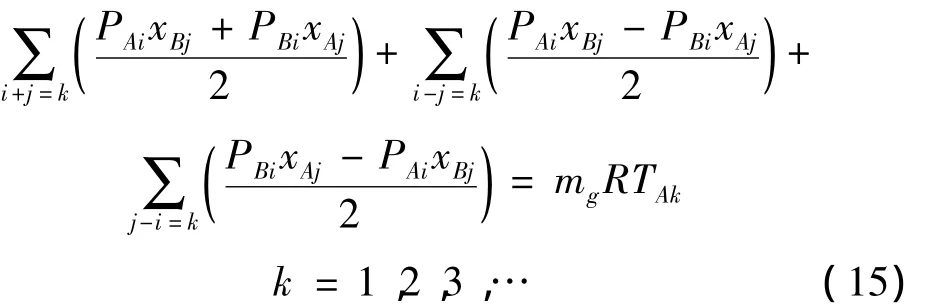
特别地，当i=j=0时有:

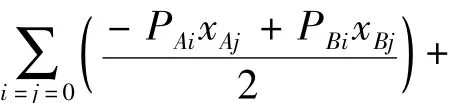
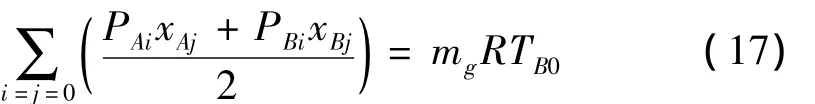
k=0的左端与k=1、2、3等相比少一项，这是因为此时第二项与第三项属于重复计算，只应保留一项。

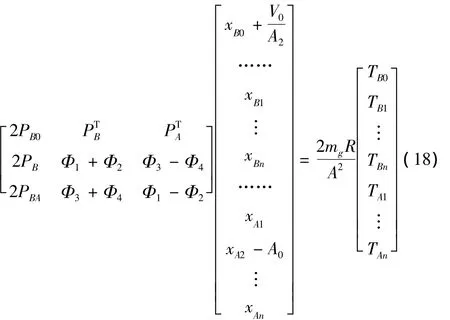
记:

则方程(15)、(16)、(17)可化为:

将式(5)～式(9)代入方程(3)，得:

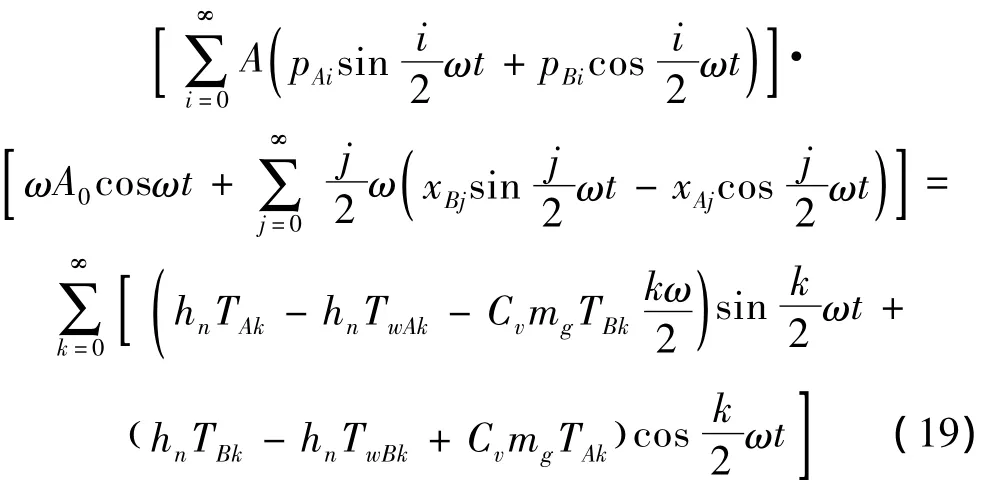
为书写简便起见，将方程中左端的ωA0cosωt合并到中，方程左端交叉相乘，将各项中的系数合并，并令其等于方程右端对应项系数，则:

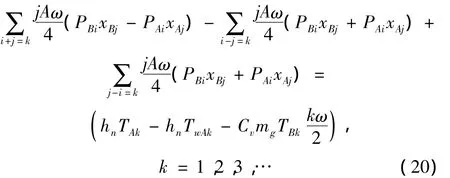
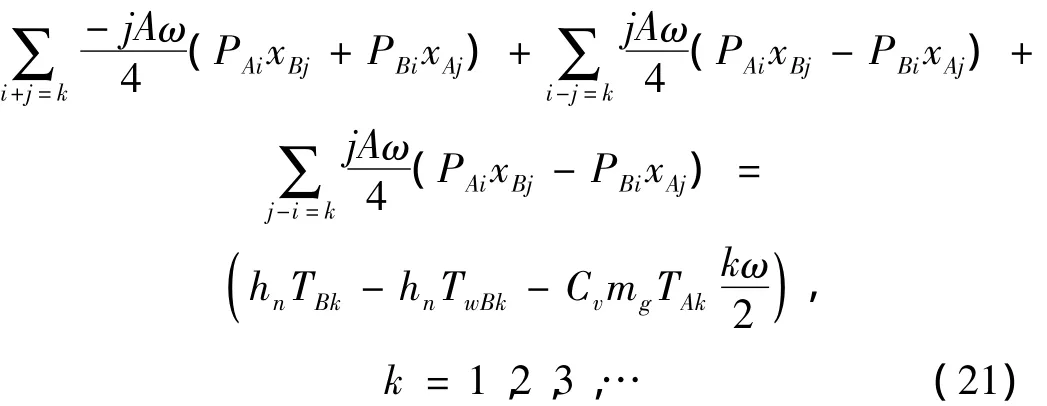
特别地，当i=j=1时有:

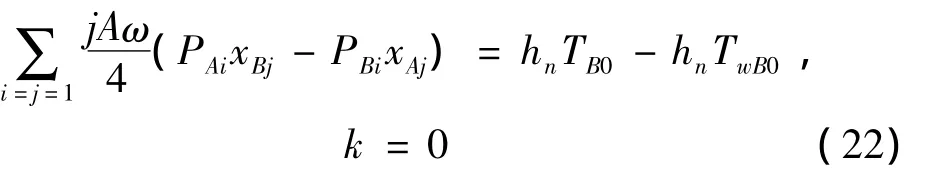
则方程(20)、(21)、(22)可化为:

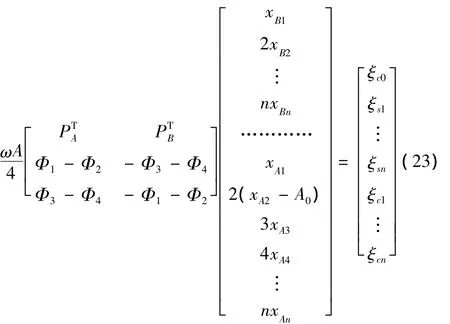
将式(6)～式(9)代入方程(4)，得:

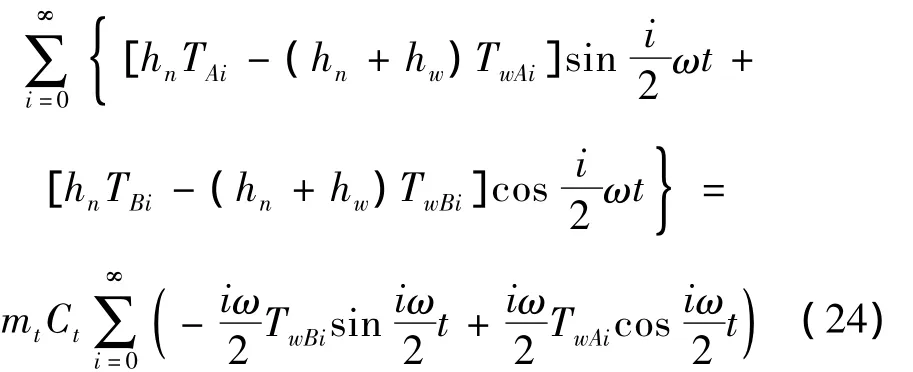
令对应项系数相等，得:

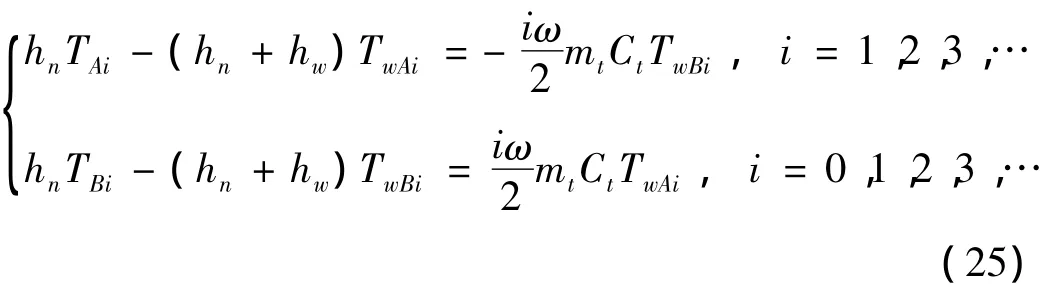
方程(25)可化为:

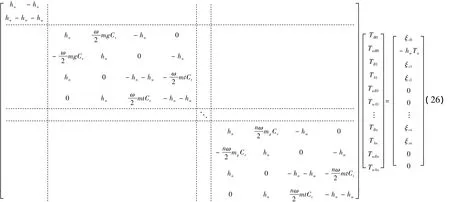
以上公式求解可用迭代法，通过计算机编程进行计算，其计算步聚按图8的流程进行。

4 算例分析

为了验证本迭代计算方法的可行性，下面对该方法进行算例分析。本算例源自某型车辆隔振，气动隔振器具有大行程，大功率重量比，无污染等优点，在豪华客车、载货汽车和高级轿车上得到越来越广泛的应用。本文所选参数为单个隔振器按比例所得，其值见表1所示。

必须说明的是，本迭代法中迭代结果与初始假设解中的项数有关，所取项数越多其解越精确，这与谐波平衡法的基本思想是一致的。该项数的取值与频率有关，从上面的仿真结果可知，在中频段，即系统线性化固有频率附近时，其非线性特性比较明显，亦即其倍/分频项比较多，所以在中频段时所取的项数要多些，其结果才会更精确;反之在低频和高频段时，系统表现出来的倍/分频分量相对要少，为了使计算简便，初始假设解中的项数可以相应取得少些。本算例中激励幅值取为0.025 m，激励频率取为20 rad/s，处于中频段比较靠近系统线性化固有频率，在其激励下，系统非线性现象比较明显，具有很好的典型性。初始假设解中的项数取10，用本迭代法进行了迭代，其迭代所得系数结果见表2所示。

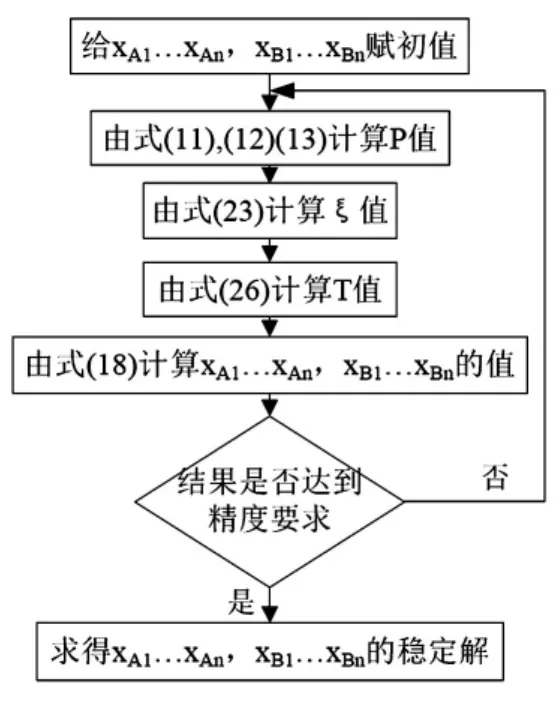
图8 求解迭代流程Fig.8 Iteration flow chart

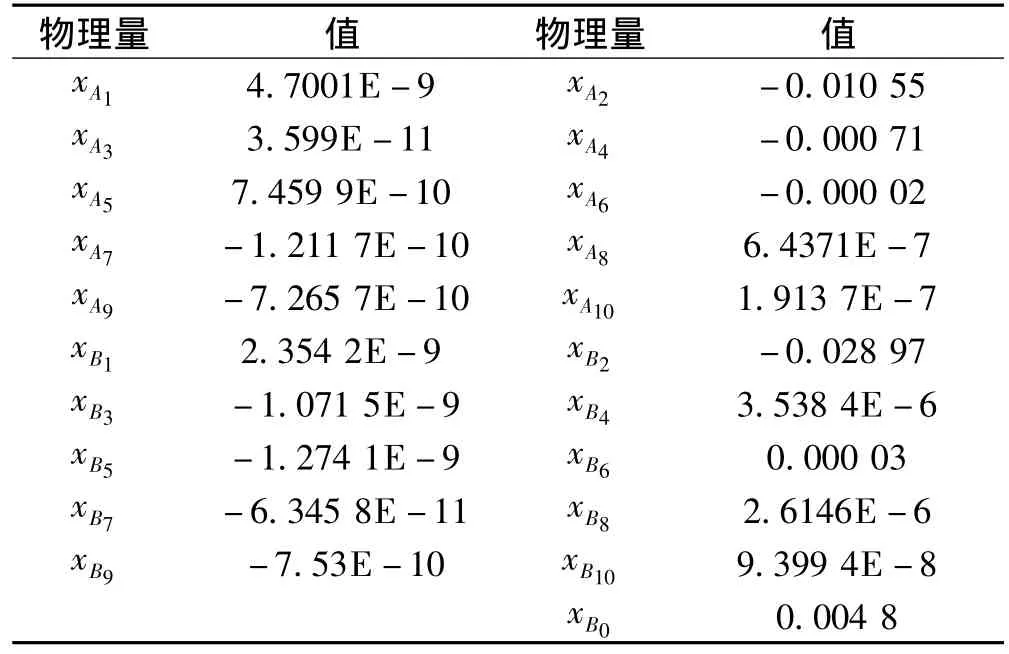
表2 系数计算结果Tab.2 Calculations of coefficients

从表2中可以看出，迭代系数中，相对偶数项系数来说基数项系数很小，即系统倍频现象明显，而分频现象微弱，从仿真曲线图2(c)中可以看出，响应频谱中出现了 20 rad/s，40 rad/s，60 rad/s，80 rad/s，100 rad/s，120 rad/s等频率，即其倍频现象很明显，和数值计算结果吻合性好。该数值计算结果和文献［12］实验所得结果也是一致的，文献［12］试验证明了空气悬架非线性振动系统的输出频率不但是异频输出，即不同于激励频率，而且输出频率基本都是激励频率的整数倍，即有很明显的倍频现象。从表2还可以看出倍数越高，系数越小，这和图5所得基频能量占系统总能量的比值接近1吻合。

图9 仿真与数值计算结果误差曲线Fig.9 Error curve of the simulation and numerical calculation results

将表2所得系数代入式(6)中，即可得振动幅值随时间变化曲线，图9是数值计算与仿真结果的误差曲线，图中仿真时间从1497 s～1500 s，此时间段系统已完全处于稳定状态。从图中可以看出，二者吻合性很好，误差很小，基本重合。

5 结论

本文建立了气动隔振系统的非线性模型，在此基础上对模型进行了仿真分析及数值计算。研究的主要结论有:

(1)系统具有很强的非线性特性，在单频简谐激励作用下，系统会出现明显的倍频、分频、零偏现象;

(2)系统在线性化固有频率附近，倍/分频、零偏现象明显，其值随激励幅值的增大而增大;

(3)在谐波平衡法的基础上，提出了一种可行的非线性数值解法，仿真与数值计算结果吻合性好，从而验证了该数值计算方法的有效性。

［1］Tomonori Kato，Kenji Kawashima，Koichi Sawamoto，et al.Active control of a pneumatic isolation table using model following control and a pressure differentiator［J］.Precision Engineering，2007，31(3):269－275.

［2］Chen Ping-chang，Shih Ming-chang.Modeling and robust active control of a pneumatic vibration isolator［J］.Journal of Vibration and Control，2007，13(11):1553 －1571.

［3］Lee Jeung-hoon， Kim Kwang-joon. A method of transmissibility design for dual-chamber pneumatic vibration isolator［J］.Journal of Sound and Vibration，2009，323(1):67－92.

［4］徐 伟，何 琳，吕志强，等.船舶主机气囊隔振系统动态特性分析［J］.振动与冲击，2007，26(7):122－124.

［5］方瑞华，解跃青，雷雨成.空气悬架理论及其关键技术［J］.同济大学学报，2003，31(9):1072－1076.

［6］潘世荣，张 军，胡水华.膜式空气弹簧在汽车座椅上的应用［J］.武汉汽车工业大学学报，1996，18(3):21－25.

［7］杨启耀，周孔亢，张文娜，等.半主动空气悬架Fuzzy-PID控制［J］.农业机械学报，2008，39(9):24－29.

［8］Koyanagi Shiro.Development of the air spring with variable nozzle［J］.Quarterly Report of RTRI(Railway Technical Research Institute)，1990，31(3):122 －127.

［9］Marcel Heertjes，Nathen van de Wouw.Nonlinear dynamics and control of a pneumatic vibration isolator［J］.Journal of Vibration and acoustics.2006，128(4):439 －448.

［10］温金鹏，李 斌，谭德伟，等.考虑织布弹性的软着陆气囊缓冲特性研究［J］.振动与冲击.2010，29(2):79 －83.

［11］陈 帅，李 斌，温金鹏，等.软着陆气囊缓冲特性与参数设置的理论研究［J］.振动与冲击.2009，28(4):25 －28.

［12］方瑞华.汽车空气悬架非线性振动理论和试验［J］.农业机械学报，2007，38(7):13 －15.

［13］尹万建.汽车空气弹簧悬架系统的非线性动力学行为研究［D］.北京:北京交通大学，2007.