运动介质中奇异边界元积分式的精确求解

杨迎春，周其斗

(海军工程大学 船舶与动力学院，武汉 430033)

边界元法是研究声辐射问题的主要数值方法之一。决定边界元法求解精度的主要因素是边界面上积分式的数值计算误差。这类积分式积分核的特点通常是含有格林函数或其在某一方向上的方向导数。特点决定了场点与源点在同一单元时积分式将具有奇性。如何精确计算奇异积分式是边界元法研究的重要课题之一。以往的文献大都只讨论静止介质条件下的计算，所用的方法主要有坐标变换法［1－3］，以及直接解析积分法［4］;Astley［5］与 Cowper［6］等也将高斯积分法用于计算。坐标变换法利用雅克比行列式与积分核分母相互约去因子来消除积分式的奇性，复杂的坐标变换会引入较多的舍入误差和截断误差。直接解析积分法只适用于特定问题，实用性不大。利用高斯积分法求解具有二阶弱奇性的积分式:Becker［7］认为对三维问题，积分核分母是源点与场点距离的二阶无穷小量，无法直接用高斯积分法求出正确的积分值;而Astley认为可以将含有奇点的单元再次剖分为更小的单元，在每一单元上重新布置高斯求积节点可以获得适当的分辨率，此方法在网格密度较高时程序实现具有很大难度。以上文献都没有给出介质运动条件下处理二阶弱奇性积分式的有效方法。

解决弱奇性积分式计算问题的关键就是要尽可能精确地求出奇点处的积分值。坐标变换和加密单元，都是为了减少奇点处的积分误差。本文主要研究介质运动条件下二阶弱奇性积分式的计算方法，首次推导出了奇点处的积分解析值。本文方法较常规方法更加易于数值实现，而且具有很高的精度。论文虽然只以三角形单元为例，但所述方法稍加变换也适用于其它形状单元，并可运用于光学等相似领域的研究。

1 二阶弱奇性积分式计算

1.1 边界积分方程中的弱奇性积分式

直角坐标系xyz中，假设介质以流速M沿z轴正向流动，则声传播方程为:

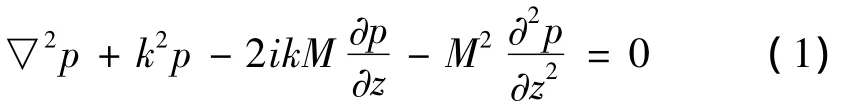
式中的p为声压，本文假定声波为简谐波，时间因数是exp(itω)，其中波数 k=ω/c，ω 是角频率，c为声速。式(1)共轭方程对应的格林函数方程为:

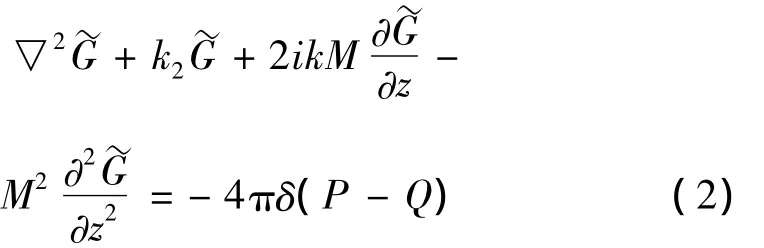
上式中 Q:(x1，y12，z1)为源点，P:(x2，y2，z2)为场点，为运动介质中的格林函数，式(2)对应的格林函数解为:

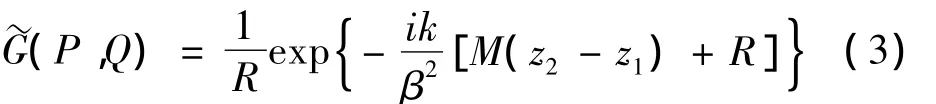
式中:

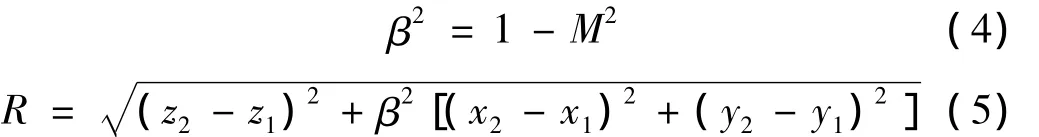
类似于静止介质中Helmholtz面积分公式的推导方法［8］，可以得到运动介质中的面积分公式:

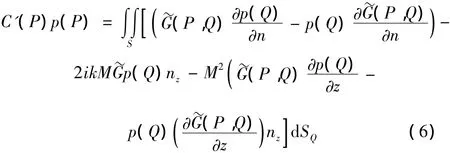
C'(P)是P点位置的函数，对外域辐射问题而言，nz是反射物面单位法向量n在z轴方向的分量，并且n指离介质。边界元计算需要对积分面S进行离散化，式(6)的离散式中将含有以下几类积分项:

三维空间中，场点与源点落在同一单元面SK上时，格林函数的分母R在场点附近趋于0，由于的分子有界，因此积分核将趋于无穷大，此时积分式在场点P处具有奇性。一般将式(7)的奇性定义为一阶弱性;而式(8)、式(9)的奇性定义为二阶弱奇性［9］。式(9)可看作是式(8)的一部分，可以用相同的方法处理。

常规数值方法，如高斯积分法，只能直接计算三维问题的一阶弱奇性积分式，若计算二阶弱奇性积分式则误差较大。为此，论文推导了一种按照积分区域的奇性，将面积分式分两部分积分的新方法:奇点部分由坐标变换计算出积分式的解析值;除奇点外单元面上的积分值，由高斯积分法求出。论文首先推导式(8)在奇点处的解析值。

1.2 二阶弱奇性积分式在奇点处的解析值

以三角形单元为例，将Sk用ΔA1A2A3表示，并建立图1所示的单元局部直角坐标系x'y'z'。

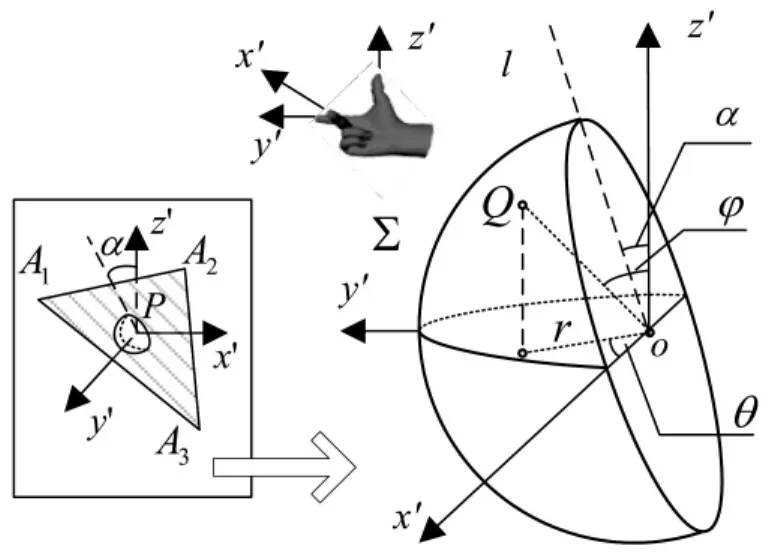
图1 运动介质中三角形单元上的半球积分面Fig.1 Integration hemispherical surface on triangle element in moving flow

局部坐标系原点o与三角形单元质心(场点)P重合;z'轴与总体坐标系中的z轴平行，并且方向相同。易证ΔA1A2A3所在平面上总存在点d，直线od与z'轴垂直。以od作为x'轴，垂直于z'轴与x'轴的直线作为y'轴。由右手法则确定x'轴和y'轴正向。平面y'oz'和ΔA1A2A3的交线l与z'轴成 α角。

记Q为球面上的任意源点，将线段oQ与z'轴的夹角表示为φ，oQ在x'oy'上的投影长度表示为r，并记r与 x'轴正向所成角为 θ，则 α≤φ≤π +α，0≤θ≤π，球坐标系与局部坐标系的关系为:

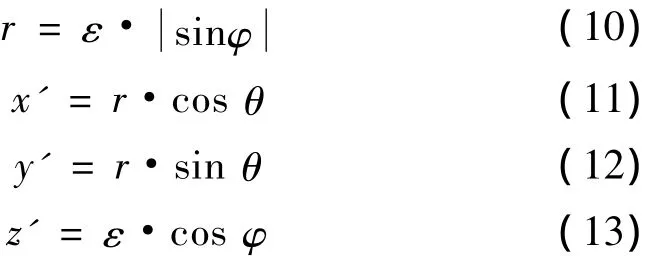
Q处的单位面法向量为:

于是可将式(8)在球面∑上的积分写为:

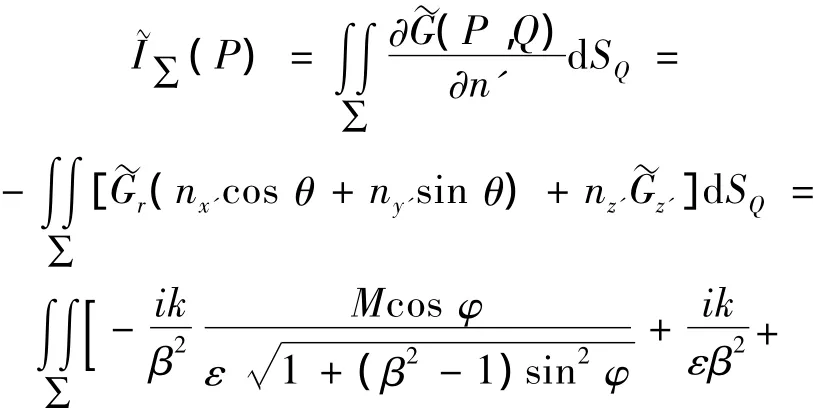
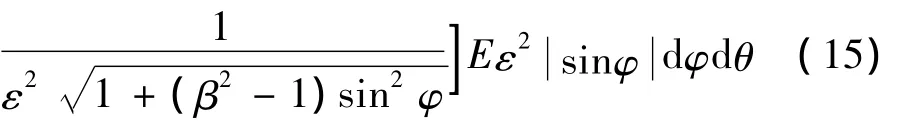
式(15)第二个等号后的负号是由源点与场点和面法线之间的相互作用关系确定的。～Gr与～Gz'分别是～G关于r和z'的偏导数。

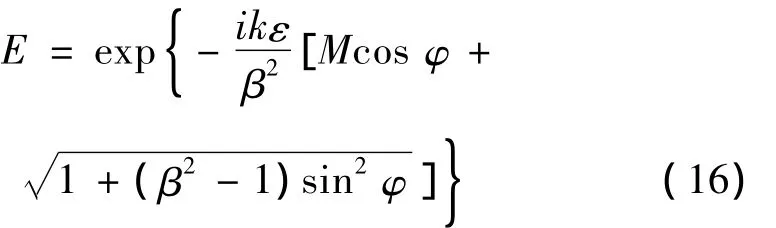
当ε→0时E→1，此时式(15)方括号中只有第三项对结果有贡献。做积分运算［10］:

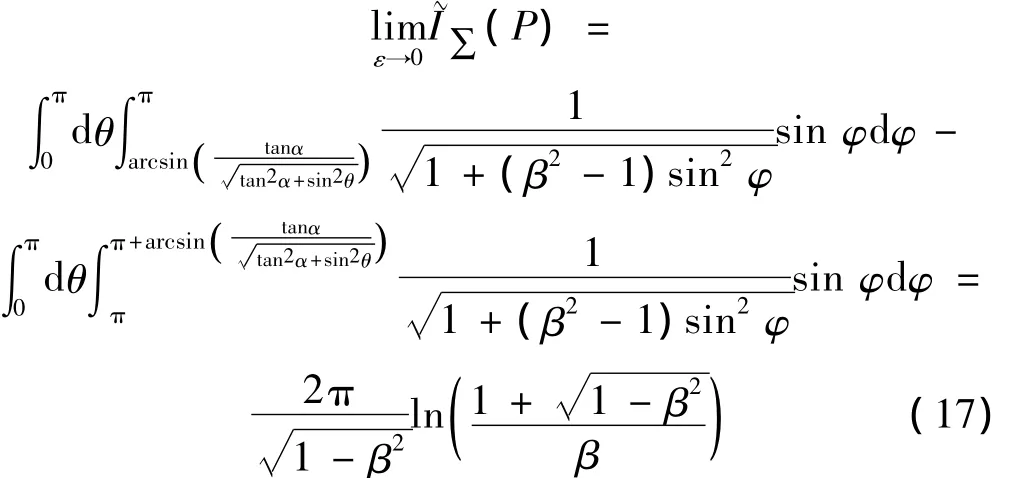
上式即为式(8)在奇点P处的解析值，并且与α无关。当M→1时，式(17)取极限为2π;本方法不适用于介质流速大于或等于1的情况。

1.3 高斯积分法

使用2.2节方法求出式(8)在奇点处的积分值后，单元Sk面上其他部分的面积分值可以用高斯积分法计算。使用高斯积分法的好处是，它可以用相对简单的迭代算法计算各种形状单元Sk上的面积分式。为了避免高斯积分法重复计算奇点处的积分值，推导了式(8)非奇性部分积分的变换式:

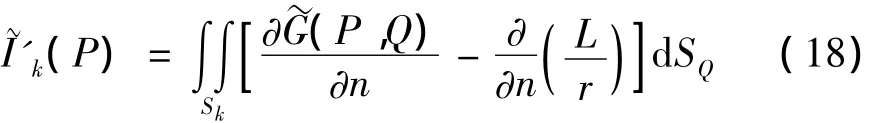
式中的r:

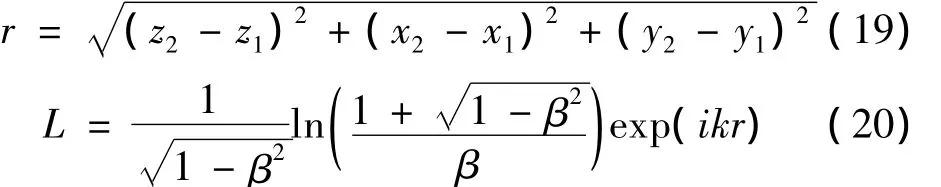
易于证明，式(18)中∂(L/r)/∂n在奇点P处的积分值与式(17)结果相同;而在其它部分的积分值为0。因此式(18)积分结果与式(8)非奇性部分的积分值相等。

论文以三角形单元的7点高斯法为例，说明如何布置高斯点以获得足够的精度，7点高斯法的详细步骤可参阅文献［10，11］。

将单元按质心(场点P)和三个顶点连线剖分为三份，如图2所示，在三个子单元上分别按照7点高斯积分法的规则布置求积节点。

由式(18)得到非奇性部分的高斯积分式为:

式中下标i表示相应的子单元编号;下标k表示子单元上相应高斯点的编号。Sk表示第i个子单元的面积，fik是式(18)的积分核在第i个子单元上的第k个高斯点处的计算值，wik是对应此点的权系数。式(21)计算结果加上式(17)表示的解析值，即可得到式(8)的完整积分值。

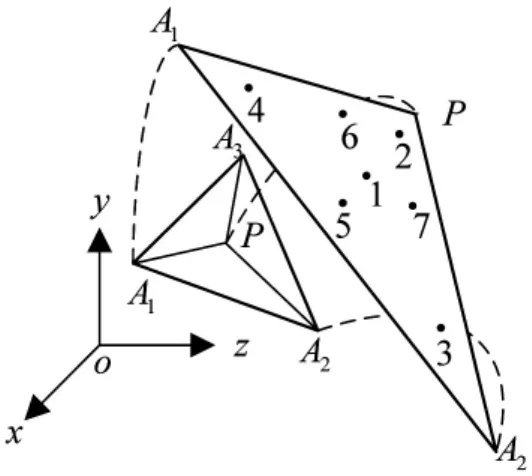
图2 三角形单元上高斯点布置方案Fig.2 The gaussian points location scheme on triangle element

对于式(7)，则将fik换为式(7)的积分核在高斯点上的计算值，式(21)计算结果即为式(7)的积分值。

对多个单元进行积分计算后发现，采用本文方法计算式(8)和式(9)要比Astley的结果具有更高的精度;而所用的子单元数目要比Astley的方法至少减小4个，求积节点密度至少减少2.25倍。

2 实验验证

为了检验方法，在流速为M的介质中作一个球径a=1 m的虚拟边界球面。球心处有一点源，球面外的部分作为外域。按照“简单源”理论［8］，点源将在球面上产生密度为σ的等效声源。等效声源在外域产生的辐射声场与点源直接在外域产生的声场，理想情况下应该相等。具体方法如下所述:

点源强度［12］满足N，对文献［12］中的点源公式进行变换，得到运动介质条件下点源在自由场中的声压解析式:

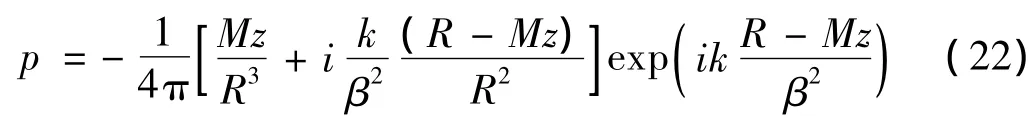
球面离散化后，由简单源理论［13］，球面任意单元k上的声压导数满足:

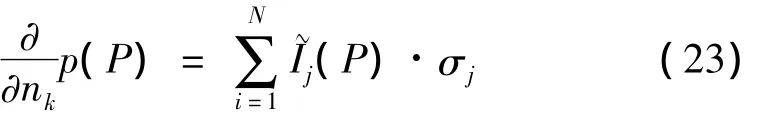
N为球面单元总数，nk是单元k上的法向量，与式(8)形式相同，σj是单元j上的源密度。场点P处的声压为:

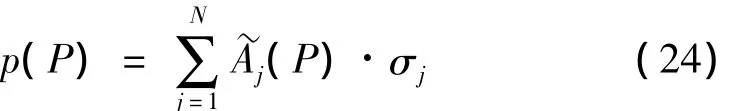
图3是球面边界元模型，共有254个节点，504个三角形单元。

计算了不同流速条件下，距球心2.5 m处的声场，0方向为流速方向，180方向为流速反向。流速为0，角频率为1000时的声压指向性如图4所示。

流速为0.5，角频率为1000条件下的声压指向性如图5所示。

图3 球面网格模型Fig.3 Meshes of sphere

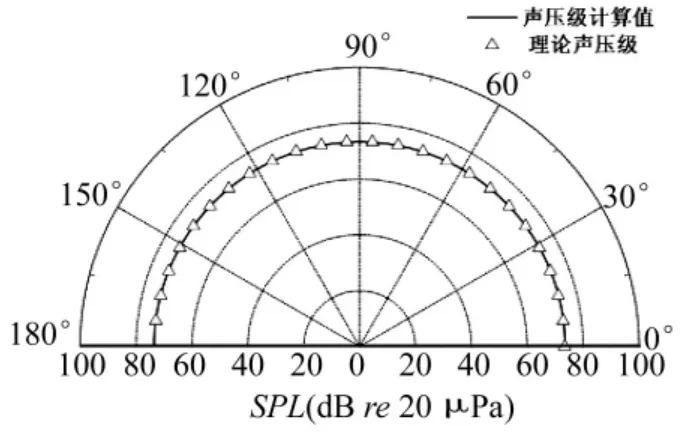
图4 声压级图(r=2.5 m，M=0，ω =1000)Fig.4 Sound pressure level(r=2.5 m，M=0，ω =1000)

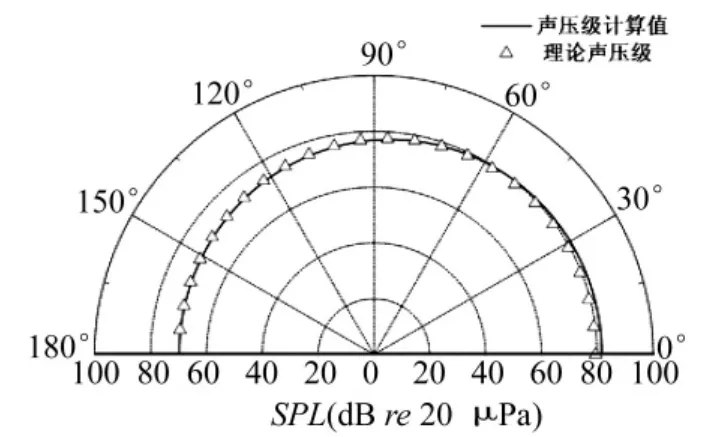
图5 声压级图(r=2.5 m，M=0.5，ω = 1000)Fig.5 Sound pressure level(r=2.5 m，M=0.5，ω = 1000)

图4、图5中的实线是数值结果，三角形点是理论值。由图可见，点声源在流速影响下的声压级具有了指向性，0角附近的声压级增大，180附近的声压级减小。由于流动介质中的计算要比静止介质中复杂，所以流动介质中的数值计算结果与解析值比较的误差相对较大。

3 结论

本文给出了三维声学边界元理论中，精确计算介质流动条件下具有奇性积分式的方法;给出了二阶弱奇性积分式在奇点处的解析值。数值实验表明，此方法与理论值符合较好。新方法与常规方法相比，更加易于编程实现，而且精度较高。

本文虽然只介绍了新方法在平面三角形单元上的应用，但本方法也可用于其它类型的单元。对于多边形平面单元，可以将其划分为多个三角形子单元分别进行积分运算;而对于曲面单元，则可借助型函数［14］先将曲面单元映射为平面单元，再用本文所述方法计算。

［1］Rizzo F J，Shippy D J.An advanced boundary integral equation method for three-dimensional thermoelectricity［J］.International Journal for Numerical Methods in Engineering，1977，11:1753－1768.

［2］Seybert A F，Soenarko B，Rizzo F J，et al.An advanced computational method for radiation and scattering of acoustic waves in three dimensions［J］.J.Aoust.Soc.Am，1985，77(2):362－368.

［3］Wu T W.Boundary Elementt Acoustics［M］.UK:WITpress，2000:51 －60.

［4］Chen JT， Chen K H. Dualintegralformulation for determining the acustic modes of a two-dimensional cavity with a degenerate boundary［J］.Engineering Analysis with Boundary Elements，1998，21(2):105 －116.

［5］Astley R J，Bain J G.A three-dimensional boundary element scheme for acoustic radiation in low mach number flows［J］.Journal of Sound and Vibration，1986，109(3):445 －465.

［6］Cowper G R.Gaussian quadrature formulas for triangles［J］.International Journal for Numerical Methods in Engineering，1973，7:405 －408.

［7］Becker A A.The boundary element method in engineering-A complete course［M］.UK:McGraw-Hill BOOK COMPANY，1992:112.

［8］Williams E G.Fourier acoustics:Sound radiation and nearfield acoustical holography［M］.San Diego:Academic Press，1999:Chapter 8.

［9］Mikhlin S G.Multi-dimensional singular integral equations［M］.Oxford:Pergamon Press，1965.

［10］数学手册编写组.数学手册［M］.北京:高等教育出版社，1979:259，1053.

［11］章本照.流体力学数值方法［M］.北京:机械工业出版社，2003:196－198.

［12］张海澜.理论声学［M］.北京:高等教育出版社，2007:232.

［13］Zhou Q，Joseph P F.A numerical method for the calculation ofdynamic response and acoustic radiation from an underwater structure［J］.Journal of Sound and Vibration，2005，283:853－873.

［14］Zienkiewicz O C，Taylor R L.The finite element method，volume 1:the basis［M］.U.K:Butterworth-Heinemann，2000:Chapter 9.