高位转换粘滞阻尼减震结构阻尼器合理阻尼系数研究

吴从晓，周 云，邓雪松，吴从永

(1.广州大学 土木工程学院，广州 510006;2广州大学 建筑设计研究院，广州 510405)

高位转换结构是指转换层位置设置超过《高层建筑混凝土结构技术规程》(JGJ3－2002)(下简称《高规》)中第10.2.2条规定的建筑，此种结构体系中转换层以下楼层中剪力墙落地较少，转换层的上下楼层刚度突变易产生薄弱层，是一种极不利于抗震的建筑结构形式［1］。随着商业化的发展、国有土地资源的紧缺和建筑使用功能的需求，目前不可避免该种体系在高层建筑的出现，为解决高位转换结构体系存在的本质问题，文献［2］和［3］提出了将耗能减震技术应用于高位转换结构体系中，形成高位转换耗能减震结构新体系，即在高位转换结构的转换层下部楼层中加入耗能减震装置(或代替原有的部分落地剪力墙)，通过耗能减震装置提供一定的附加阻尼或附加刚度来改变结构的动力特性，并利用耗能装置耗散输入结构的地震能量，对结构进行减震控制，减轻或避免结构在地震中产生破坏或倒塌。文献［4～6］对高位转换耗能减震结构体系进行了弹性和静力弹塑性分析研究，得出该种结构体系是可行的，并且采用该种耗能减震结构体系后能很好的改善原高位转换结构的抗震性能。

高位转换结构作为目前各城市建筑中采用较多的结构形式之一，由于其自身抗震性能差的缺点，采用被动控制的高位转换耗能减震结构必将成为主导体系之一，然而，我国现行的《建筑抗震设计规范》(下简称《抗规》)和《高规》相关章节中对高位转换耗能减震结构的设计方法与内容方面都没有涉及，从而制约了高位转换耗能减震结构体系在实际工程中的应用，为此，本文结合目前规范中对高位转换结构体系的框支层的层间位移角和结构的等效侧向刚度的限制要求，基于振型分解反应谱理论，通过调整框支结构刚度后，在满足规范要求的等效侧向刚度比和层间位移角限值前提下，调整结构的顶点位移与不调整结构框支层结构刚度的粘滞阻尼减震框支层减震结构等效阻尼比计算方法，推导出高位转换粘的顶点位移相等或相近的基础上，结合反应谱理论和线性粘滞阻尼减震结构等效阻尼比计算方法，推导出高位转换粘滞阻尼减震结构阻尼器的合理阻尼系数计算公式，该方法计算公式简单实用，可为指导高位转换耗能减震结构设计提供依据。

1 粘滞阻尼系数推导

1.1 计算模型

由于高位转换结构体系的转换层位置一般都布置于结构第三层以上，根据现有的研究成果和《高规》附E中的要求，对底部大空间层数大于1层时计算结构等效侧向刚度的结构模型作为结构本文的计算模型1(本文介绍的模型1中框支层的层间位移角和等效侧向刚度比是不满足规范要求，在模型框支层中需布置粘滞阻尼器，并且阻尼器在转换层以下楼层采用均匀连续布置)，如图1所示，模型中转换层上部结构总高度H2应与下部结构总高度H1接近，并且不应大于H1。对模型1中转换层以下框支层的剪力墙的数量或柱截面进行调整，使模型计算出的等效侧向刚度比满足高规中式(E.0.2)要求，此时的新模型为本文计算模型2。

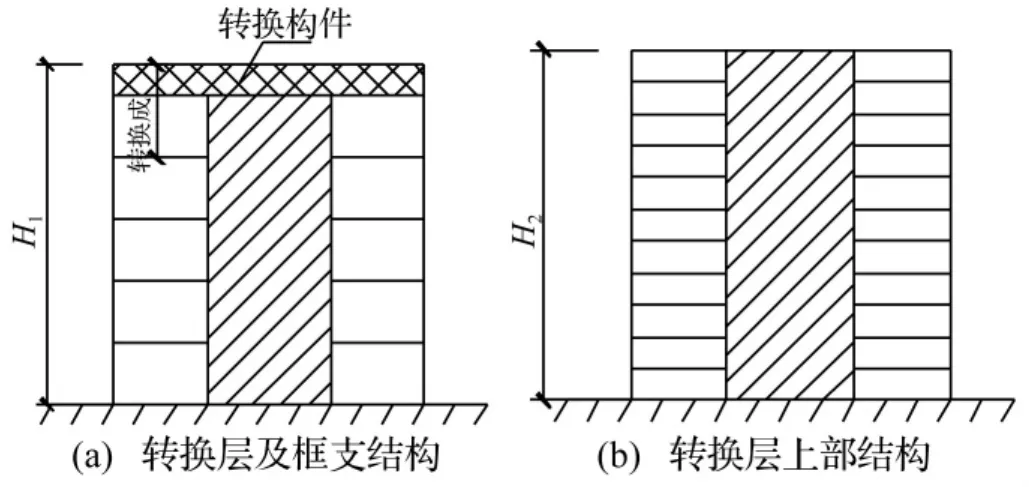
图1 计算模型Fig.1 Calculation models

1.2 结构顶点位移

对模型2进行地震作用下的反应谱分析，得出结构的顶点位移ystif，根据本文的前提条件，即模型1中框支层顶点位移和模型2框支层顶点位移相等，可得出:

式中:ystif为调整剪力墙数量或柱截面后模型2框支结构顶点位移;y1为布置粘滞阻尼器模型1的框支结构顶点位移。

根据结构动力平衡条件，布置粘滞阻尼器的多质点耗能减震结构的运动方程为［7］:

式中:CD为粘滞阻尼器具线性粘滞系数或等效粘滞系数矩阵;Cs为原结构阻尼系数矩阵;ξD为粘滞阻尼器的附加阻尼比;ξs为原结构阻尼比;M为结构质量矩阵;K为结构刚度矩阵分别为结构的加速度、速度和位移向量;ωn为结构第n阶圆频率。

为了使方程(3)能进行振型分解，则需要使结构的非比例阻尼矩阵对角化［8］，由瑞雷阻尼理论可得:

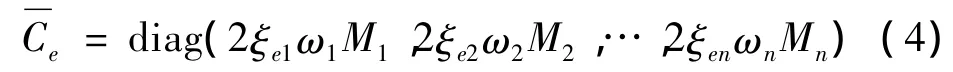
式中:M1，…，Mn为结构各振型广义质量，即 Mi=MA，A为结构振型矩阵。i

根据式(3)，结合振型分解反应谱法可得模型1——高位转换粘滞阻尼减震结构中框支结构顶点位移，即:

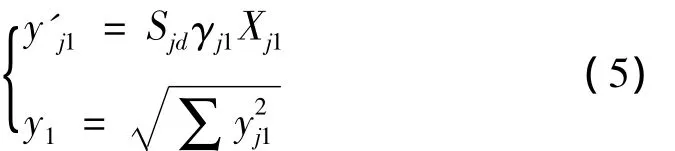
式中:y'j1为第j振型转换层以下结构顶点位移;Sjd为第j振型转换层以下结构的位移谱值;γj1为第j振型参与系数;Xj1为第j振型转换层以下结构顶点的水平相对位移。

将式(1)代入式(5)中，等式中只有未知谱位移参数，谱位移参数与结构的阻尼比是相互关联的，为此，通过计算谱位移参数，可推导模型1在满足式(1)条件下粘滞阻尼器需附加给结构的阻尼比，从而得出粘滞阻尼器粘滞阻尼系数。当模型1转换层以下框支层数较少时(小于8层)，可采用简化方法计算，计算时可不考虑扭转振型效应对结构顶点位移的影响。

1.3 粘滞阻尼系数计算

为了求出高位转换粘滞阻尼减震结构转换层以下框支层的顶点位移，则需求结构的位移反应谱，根据文献［8］～［13］，将《抗规》中的加速度反应谱进行转换可得到位移反应谱，即:

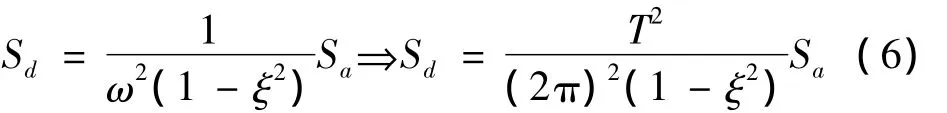
式中:Sd为位移反应谱;Sa为加速度反应谱;ω为结构频率;ξ为结构阻尼。

对于高位转换结构体系，转换层以下框支层的楼层层数一般都大于3层，为此，转换层以下框支层结构周期基本都大于0.1 s，并且在多数情况下结构转换层布置的位置的楼层数也不会超过20层，由高层结构周期的估算公式，可确定转换层以下框支层结构的周期在0.1≤T≤Tg，则模型 1——高位转换粘滞阻尼减震结构中框支结构的位移反应谱曲线为:

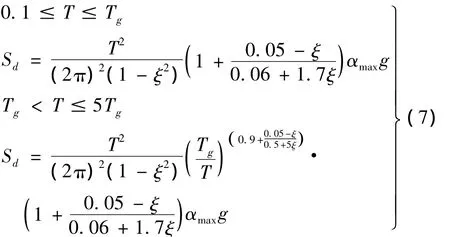
由式(1)～式(7)可求得布置粘滞阻尼器高位转换耗能减震结构转换层以下楼层的粘滞阻尼器的附加阻尼比 ξe1，…，ξen。

采用ETABS软件或SAP2000软件，对调整阻尼比后的模型1中的框支层结构进行反应谱分析，得出结构的层间位移和楼层剪力(在计算过程中由于阻尼器安装施工中的缝隙及其它因素的影响，当阻尼器两端的位移采用结构层位移值计算时，应对其值进行折减［14，15］)，由《抗规》公式(12.3.4 － 1 ～ 12.3.4 － 3)可得:

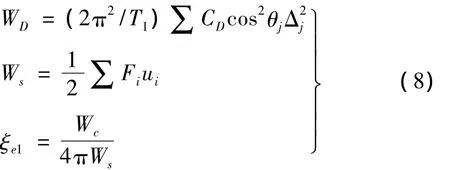
式中:WD为所有阻尼器往复一周消能的能量;Ws为结构的总应变能;Δj为第j个阻尼器两端的相对水平位移;θj为第j个阻尼器方向与水平方向的夹角;T1为结构的基本周期。

由式(8)可反算出结构中附加粘滞阻尼器的等效线性粘滞阻尼系数CD。

2 算例

2.1 结构概况

某20层高位转换结构，在结构第七层顶设置转换大梁，结构的平面布置如图2所示，结构2层和7层楼层层高为4.5 m;2～6层楼层层高为4.2 m，转换层以上楼层层高为3 m，构件的截面尺寸如表1所示，结构楼面活载为2.0 kN/m2，设计地震分组为第1组，场地类别为Ⅱ类，设防烈度为8度，设计基本加速度0.2g。

表1 构件参数Tab.1 Model parameters

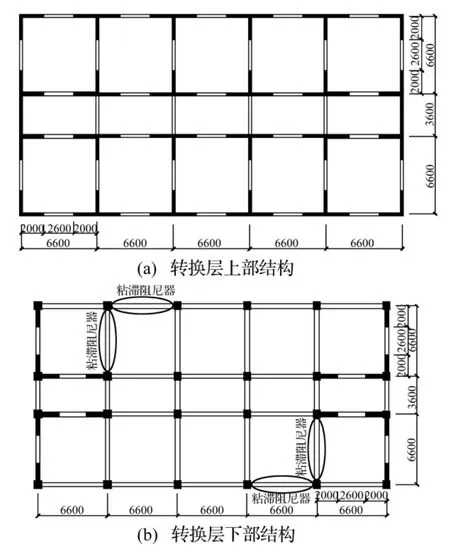
图2 模型1平面图Fig.2 Plans of model 1

2.2 分析结果

对原算例转换层以下框支结构进行修改形成模型2，平面如图3所示。按照《高规》计算得出结构等效侧向刚度比 γey=1.006、γex=0.97，基本能满足《高规》要求，采用反应谱法计算结构顶点位移yystif=15.54 mm、yxstif=13.88 mm，为使结构两轴方向的阻尼比接近，则y1=14.66 mm。由上节计算方法计算得出高位转换粘滞阻尼减震结构框支层顶点位移为14.66 mm时，结构总阻尼比ξ=0.266，则需要布置粘滞阻尼器的粘滞阻尼系数为CD=276 kN·s/mm。根据计算出的粘滞阻尼系数值，在框支层每层布置四组阻尼器，则每个阻尼器的线性阻尼系数取140 kN·s/mm，采用单斜支撑布置形式，阻尼器布置位置如图2(b)所示。

对高位转换粘滞阻尼减震结构(模型1)和普通结构(模型2)采用ETABS软件进行反应谱和时程分析，时程分析采用神户波(KOBE波)和北岭波(NORTHRIDGE波)，按规范要求调整地震波的峰值加速度。结构周期如表2所示，反应谱和时程分析的楼层剪力和层间位移角如图4～图5所示。从分析结果中可以看出，高位转换耗能减震结构的抗侧刚度明显小于普通结构，然而高位转换耗能减震结构的楼层剪力明显小于普通结构，减小约为50%;高位转换耗能减震结构在转换层以下框支结构的层间位移角也能满足规范要求的限值，与普通结构基本相同，但转换以上剪力墙结构的层间位移角明显的小于普通结构，减小也约为50%，可能会加大转换层附近结构层间位移的突变，对结构的抗震性能不利，为此，高位转换耗能减震结构体系易同时采用位移型和速度型耗能减震装置进行综合控制结构的地震反应，减小转换层位移突变。

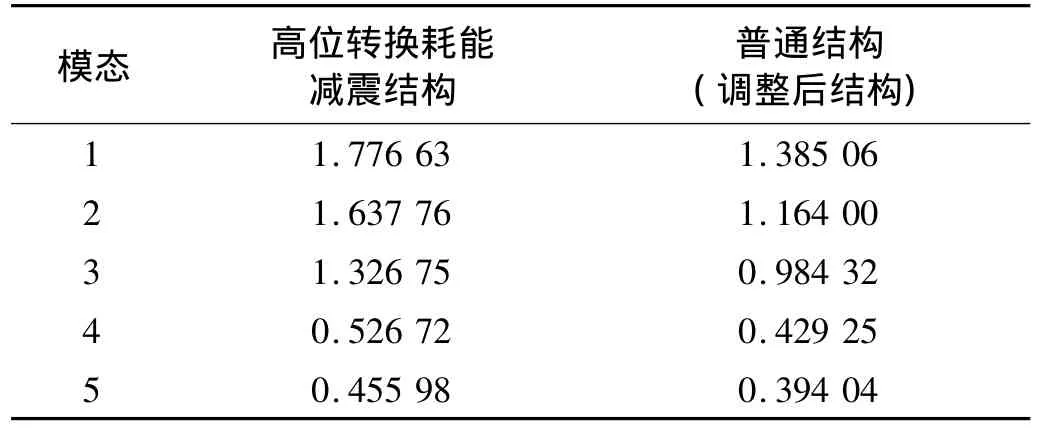
表2 结构周期Tab.2 Structural periods

图3 调整后平面图(模型2)Fig.3 Plans of model 2

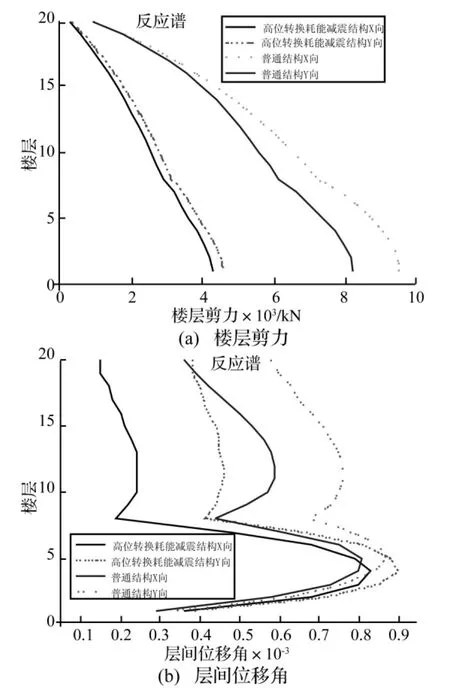
图4 反应谱分析结果Fig.4 Analysis results under response spectrum action

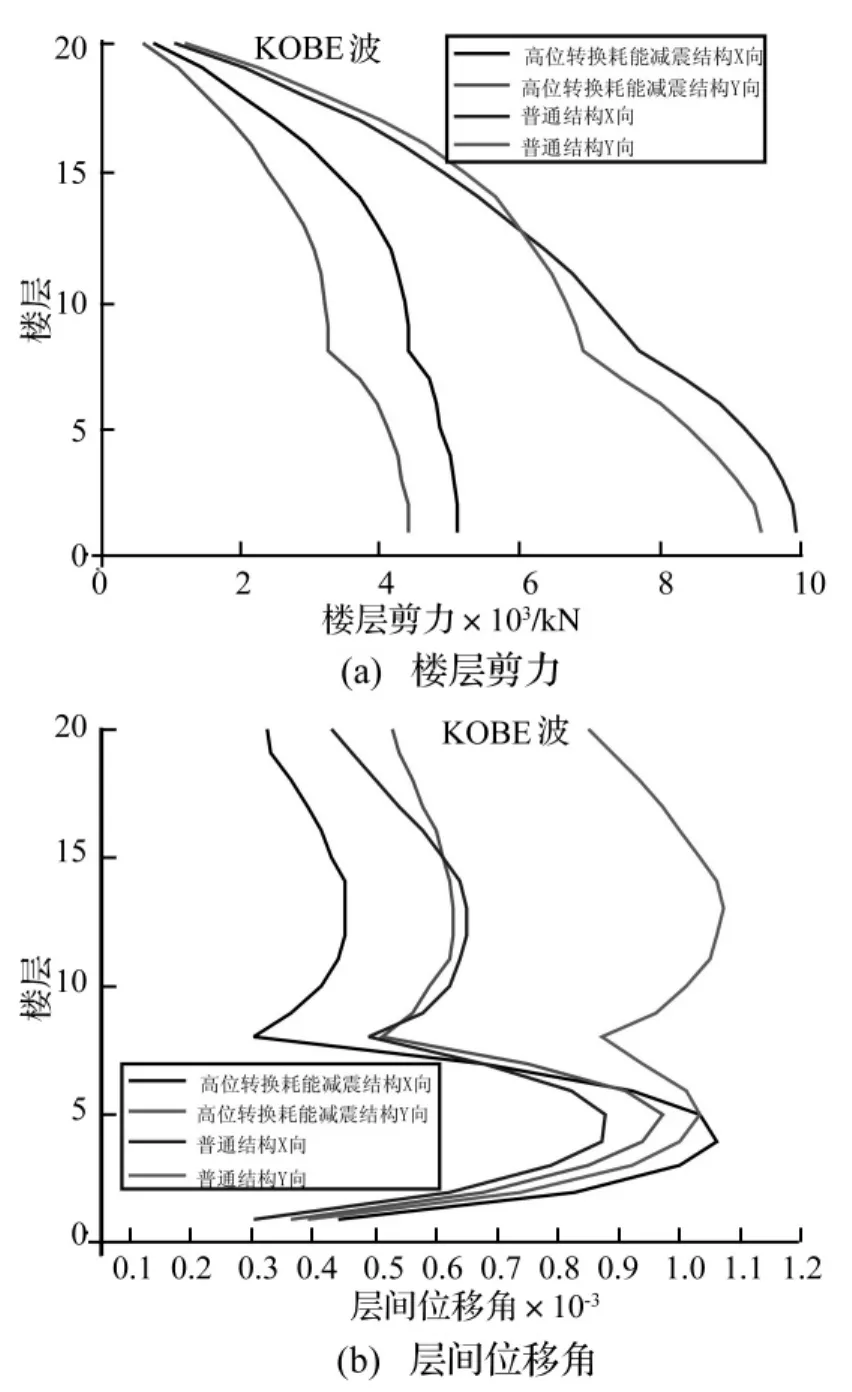
图5 KOBE波分析结果Fig.5 Analysis results under KOBE wave action

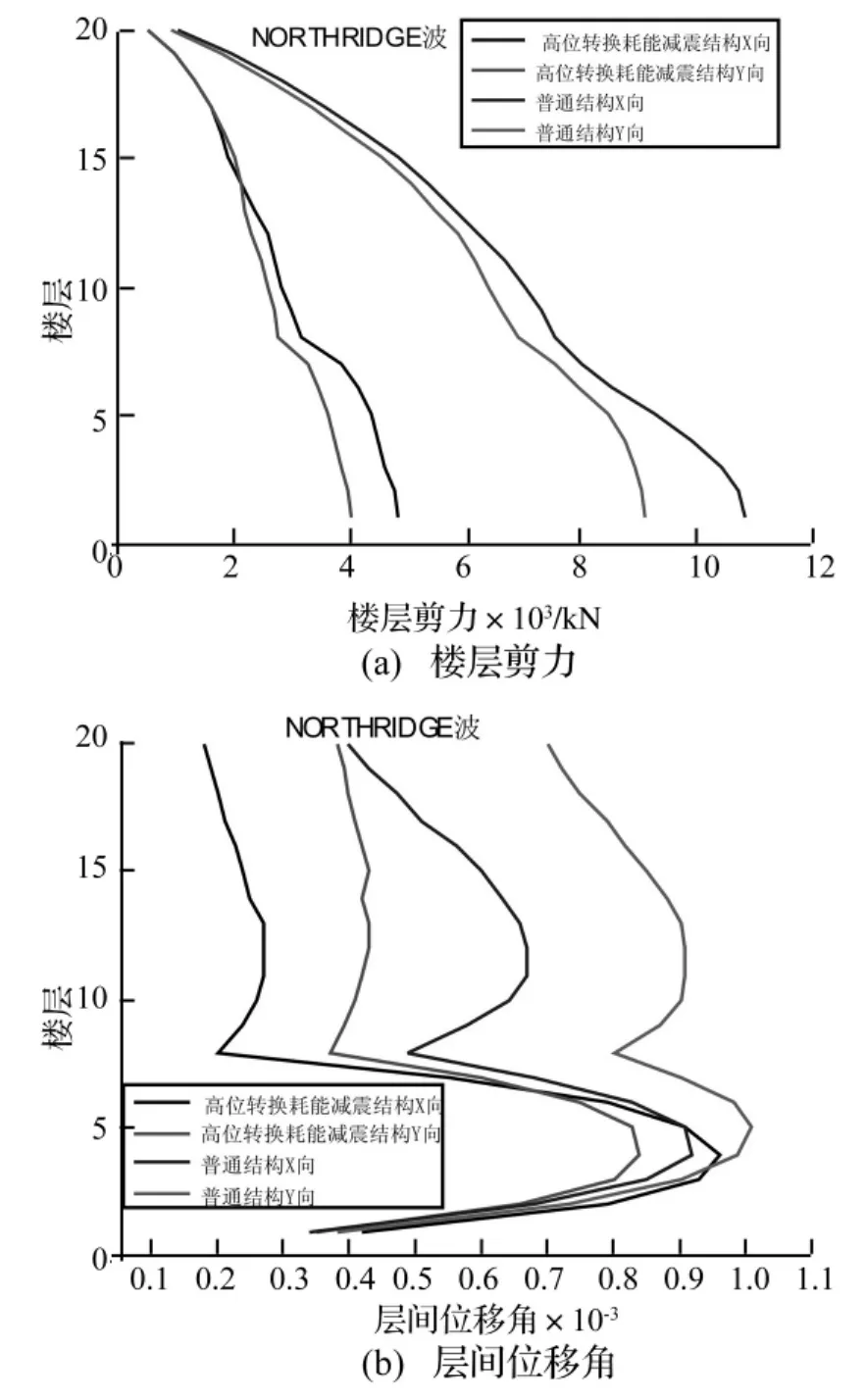
图6 NORTHRIDGE波分析Fig.6 Analysis results under NORTHRIDGE wave action

3 结论

本文对高位转换粘滞阻尼减震结构中粘滞阻尼器的合理阻尼系数取值进行了研究，得出以下结论:

(1)基于本文提出的高位转换粘滞阻尼减震结构的合理粘滞阻尼系数计算方法是可行的。

(2)采用高位转换粘滞阻尼减震结构同样能达到通过增加转换层以下框支层抗侧刚度方法(增加剪力墙数量)来满足规范限值要求，并且采用高位转换粘滞阻尼减震结构后结构的层剪力明显小于普通结构，结构抗震性能得到了进一步改善。

(3)高位转换耗能减震结构体系易同时采用位移型和速度型耗能减震装置进行综合控制方法或减少转换层上部剪力墙的数量实现更好的地震反应控制效果。

［1］徐培福.复杂高层建筑结构设计［M］.北京:中国建筑工业出版社，2005.

［2］周 云，吴从永，邓雪松，等.高位转换耗能减震结构新体系［J］.工程抗震与加固改造，2006，28(5):72－77.

［3］周 云，邓雪松，吴从晓.高层耗能减震结构体系概念和实现［J］.工程抗震与加固改造，2007，29(6):1－9.

［4］吴从晓.高位转换耗能减震结构体系分析研究［D］.广州:广州大学，2007.

［5］吴从晓，周 云，邓雪松，等.高位转换耗能减震结构体系静力弹塑性分析［J］.土木工程学报，2008，41(9):54－59.

［6］Wu Congxiao，Zhou Yun，Deng Xuesong，et al.Analytical study on seismic performance of the structure of high-level transfer with energy dissipation devices［C］.Guangzhou:South China University of Technology Press.International Symposium on Innovation＆Sustainability of Structures in Civil Engineering.2009:1650 －1655.

［7］郑久建.粘滞阻尼减震结构分析方法与设计理论研究［D］.北京:中国建筑科学研究院，2003.

［8］周 云.粘滞阻尼减震结构设计［M］.武汉:武汉理工大学出版社，2006.

［9］Lin Y Y，Chang K C.An improved capacity spectrum method for ATC-40［J］.Earthquake engineering and structural dynamics，2003，32:2013 －2025.

［10］周 云.金属耗能减震结构设计［M］.武汉:武汉理工大学出版社，2006.

［11］周 云.摩擦耗能减震结构设计［M］.武汉:武汉理工大学出版社，2006.

［12］周 云.粘弹性减震结构设计［M］.武汉:武汉理工大学出版社，2006.

［13］周 云.耗能减震加固技术与设计方法［M］.北京:科学出版社，2006.

［14］日本隔震结构协会.被动减震结构设计·施工手册［M］.蒋 通译.北京:中国建筑工业出版社，2008.

［15］翁大根，黄 伟，吕西林.钢框架消能减震体系研究与工程应用［C］//北京:科学出版社，第一届全国防震减灾工程学术研讨会，2005，广州.