煤块冲击破碎速度研究

刘 瑜，杜长龙，付 林，高魁东

(中国矿业大学 机电工程学院，徐州 221116)

煤块破碎是煤炭洗选的一个重要生产环节，它可以使原煤更适合洗选加工，也可以使产品煤满足用户对粒度的需求［1］。冲击破碎具有破碎比大和能耗低的优点，同时兼有中碎和细碎的双重作用，是煤块破碎的主要方法［2］。为提高冲击破碎的能量利用率，增加冲击破碎的生产能力，需要对煤块冲击破碎过程进行分析，确定其主要设计参数——冲击破碎速度的取值范围。

目前国外学者［3－6］对冲击破碎的研究多集中于冲击式破碎机的破碎性能，都没有对破碎时自由煤块与冲击板冲击碰撞过程进行分析，无法准确获得破碎所需的冲击速度。国内已有一些学者进行了冲击速度的研究，但多是采用数值模拟和计算机仿真方法。房琳等［7］用有限元方法通过MSC.Dytran软件对板锤冲击煤块的过程进行了仿真，得到了冲击过程中使破碎力损失较小的冲击速度。LI Fang-wei和 LI Yan-huan等［8］通过LS-DYNA软件对煤岩冲击破碎过程进行模拟，得到破碎煤需要的冲击速度值约为10 m/s。由于煤块形状的随机性和内部结构及材料性质的复杂性，通过计算机建立的冲击模型对煤块的形状、结构等进行了简化，与实际煤块存在差异，分析结果的必然与实际情况存在误差。曾洪茂和周恩普［9］从Hertz的冲击破碎基本定律出发，推导了冲击速度的数学表达式，但是在他们的推导过程中没有考虑破碎的能量损失，因此得到的理论冲击速度小于实际冲击速度。

本文将对自由煤块与冲击板冲击破碎过程进行分析，基于非线性接触模型［10，11］和裂缝假说确定煤块破碎所需的冲击速度，并通过煤块冲击破碎试验，修正冲击速度的理论表达式，得到与煤块自身物理性质相关的冲击速度计算模型，为煤块破碎时冲击速度的初选提供理论依据。

1 煤块冲击破碎速度

1.1 煤块冲击过程动力分析

为便于理论分析，首先做如下假设:

(1)煤块是半径为R的球体，且在冲击过程中不发生破碎。

(2)冲击板为刚性无限大平板，碰撞时不产生变形。

煤块与冲击板的冲击碰撞过程如图1所示，图中v1为煤块的冲击速度，δ为煤块冲击过程中的最大变形量，v2为煤块反弹后的速度。从图1可以看出，煤块与冲击板的碰撞过程可以分为压缩和恢复两个阶段，这两个阶段以煤块变形量最大的时刻为分界点。

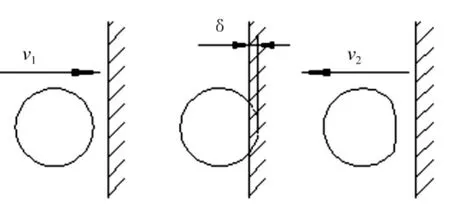
图1 煤块冲击过程分析Fig.1 Analysis of impact for lump coal

煤块是非线性脆性材料，内部存有裂隙，在碰撞阶段裂隙被压密会产生不可恢复的塑性变形。根据文献［10］的论述，脆性材料碰撞并且产生塑性变形的应该选择分段塑变碰撞模型。因此，煤块和冲击板的冲击过程用非线性接触模型来表示［11］:

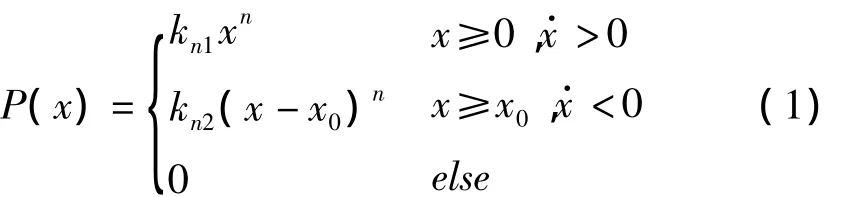
式中:P(x)为接触力;x为变形量;n为变形量幂次，n=;kn1为压缩阶段的接触刚度［12］，对于煤块和冲击板的冲击过程有，i=1，2，其中Ei和vi分别为两接触体的弹性模量和泊松比，下标"1"表示煤块，下标"2"表示刚体;kn2为恢复阶段的接触刚度;x0为煤块的不可逆变形量。

根据压缩阶段能量守恒，可以得到最大变形量xmax和最大接触力Pmax的表达式:

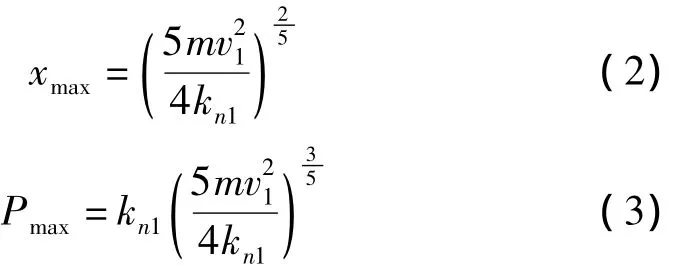
对应的内应力为:

式中:m为煤块的质量;ρ为煤块的密度。

1.2 煤块冲击破碎速度范围

煤块若要发生破碎，必须满足内应力大于煤块开始破碎时的极限应力，根据文献［13］中的分析，煤块破碎的极限应力为:

式中:γ为煤块增加单位表面积所需的表面能。

煤块冲击破碎所需要的应力必须满足σ≥σc，结合公式(4)，可以得到煤块发生破碎需要的冲击速度范围:

该公式为煤块发生破碎所需要的最小冲击速度，当冲击速度大于该数值时，煤块才有可能发生破碎。对于煤块的破碎，人们关心的是破碎后煤块的粒度，为此需要得到煤块被破碎到指定粒度所需要的冲击速度。

1.3 煤块破碎到指定粒度需要的冲击速度

常用的煤岩破碎理论有面积假说、体积假说和裂缝假说。由于实际煤块中存在很多裂隙，适合选择裂隙假说进行煤块的冲击破碎速度计算。

根据裂缝假说将体积为V的煤块从粒度Dp破碎到粒度dp所需的功耗为:

式中:KB为裂缝假说系数，可由试验得来。

煤块冲击碰撞过程中的能量转化关系有下面两种情况:

(1)煤块与冲击板冲击但不发生破碎。在这种情况下，煤块的初始能量——动能，在压缩和恢复两个过程中，被内部阻尼所损耗，因此初始的动能主要转变为阻尼损耗的能量和碰撞后煤块的动能，阻尼损耗的能量通过恢复系数体现。

(2)煤块与冲击板冲击且发生破碎。在这种情况下，内部阻尼仅在压缩阶段损耗能量，在压缩结束时煤块的内应力达到破碎应力，煤块发生破碎，其初始动能主要转变为压缩阶段的阻尼损耗能量和使煤块破碎的能量。

压缩阶段阻尼消耗的能量可以近似认为是压缩和恢复两个阶段阻尼所损耗的总能量的一半，即:

式中:WYZ为压缩阶段阻尼损耗的能量;WZ为整个冲击过程阻尼损耗的能量，e为碰撞恢复系数。

冲击破碎过程中的能量转化可以表示为:

式中:ET为煤块的初始能量，ET=12mv21;W为煤块的破碎能量。

由式(6)～式(7)可得用冲击破碎方法将质量为m的煤块由粒径Dp破碎到粒径dp所需的功耗为:

将式(5)代入式(8)，可以得到将煤块由粒径Dp破碎到粒径dp的冲击速度:

通过式(6)和式(11)可以确定煤块破碎需要的冲击速度。对于冲击式破碎机，其最小冲击速度可以通过式(6)获得，如果需要获得指定破碎粒度的产品煤，则需要结合式(11)来确定具体的冲击速度。

2 冲击破碎速度的试验修正

2.1 冲击试验设计

从新汶矿业集团协庄煤矿采集煤块进行试验，研究煤块破碎情况。试验之前，对煤的性质进行测量，得到试验煤块的平均普氏硬度为1.364，抗压强度为13.5 MPa。

依据重复原则、随机化原则和区组控制原则将试验确定为双因素四水平不等重复试验，且重复试验次数原则上不少于7次。结合常用破碎机破碎煤块的粒度分布情况和式(6)、式(11)理论冲击速度计算值，确定破碎粒度和冲击速度的四个水平值，如表1所示。共试验煤块235块，破碎121块，试验时量取煤块破碎前后的最大尺寸，并记录试验冲击速度，为后续研究提供依据。

表1 冲击破碎试验影响因素的水平值Tab.1 Level of factors in impact crushing expe riment

2.2 冲击破碎速度拟合公式

式(9)的等号右边由常数组成，在进行冲击速度公式修正时，将式子右边的前半部分视为一个未知数。式中含有两个不相关的量，即破碎前后的粒度值，因此必须进行多元回归分析。

常用的多元回归分析方法有线性和非线性两种。通过试算，线性回归方法得到的估计结果与试验测量的速度值误差太大，故采用非线性的多元回归分析。Matlab中的"nlinfit"函数专门用于非线性的最小二乘数据拟合，通过多次验证，采用如下形式的非线性模型能够较好的拟合试验数据:

式中:bi为常系数，i=1，2，…，6，可以通过试验数据获得。用协庄矿煤块的破碎试验数据进行拟合，可以得到适合于该煤矿的拟合系数:

将协庄矿拟合数据绘制曲面并与试验值对比，如图2所示。经计算有53.92%的拟合冲击速度值和试验值的误差小于5%，88.23%的拟合值与试验值误差小于10%，精度较高。

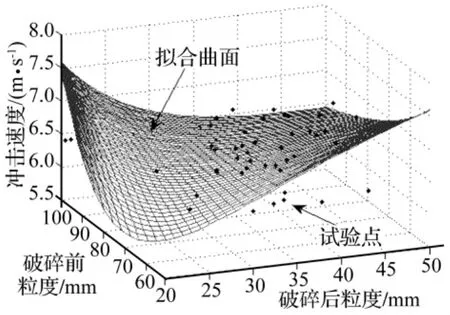
图2 拟合曲面与试验散点对比Fig.2 Comparison of fitting surface and experiment points

2.3 冲击破碎速度公式修正

式(12)拟合精度高，但是结构形式比较复杂，并不适合作为冲击破碎速度的初选公式，因此要利用试验数据对理论公式进行修正，得到适合工程应用的冲击破碎速度初步选择依据。

式(9)表明冲击破碎速度是破碎前后粒度的一次函数，经计算实际冲击破碎速度与理论速度相差不大，因此考虑在理论计算公式上添加修正系数，即:

式中:ai为常系数，i=1，2，可以通过试验数据获得。结合试验数据，对于协庄煤矿的煤块，有a1=0.075，a2=－0.493。

将修正后的冲击破碎速度理论值与试验值进行比较，有50%的理论值与试验值误差小于10%，70%的理论值与试验值误差小于15%，85%的理论值与试验值误差小于20%。这表明理论修正公式具有较高的精度，可以作为冲击破碎速度初选的理论依据。

3 结论

考虑煤块的脆性以及碰撞过程中的塑性变形，采用分段塑变模型得到了煤块与冲击板碰撞过程中的接触力。以裂缝假说为基础推导了煤块冲击破碎速度的理论公式，并以此为基础进行了冲击破碎试验。通过对试验数据的分析，得到冲击破碎速度的试验拟合公式和理论修正公式。通过两个公式的比较得出，试验拟合公式精度很高，但结构形式复杂，可以作为精确破碎的速度选择依据，理论修正公式能够满足工程应用所需的精度要求，且结构形式简单，适合作为初级破碎时冲击破碎速度的理论选择依据。

［1］智玉莲，韩志强，庞 怡.石料的筛分与破碎［M］.北京:人民交通出版社，1991.

［2］全国煤炭技工教材编审委员会.选煤机械［M］.北京:煤炭工业出版社，2002.

［3］Sadrai S，Meech J A，Ghomshei M，et al.Influ-ence of impact velocity on fragmentation and the energy efficiency of comminution［J］. International Journal of ImpactEngineering，2006，33(1－12):723－734.

［4］Nikolov S.Aperformance model for impact crushers［J］.Minerals Engineering，2002，15(10):715－721.

［5］Nikolov S.Modelling and simulation of particle breakage in impact crushers［J］. InternationalJournalofMineral Processing，2004，74(1):219 －225.

［6］Tavares L M，Carvalho R M.Impact work index prediction from continuum damage model of particle fracture［J］.Minerals Engineering，2007，20(15):1368－1375.

［7］房 琳，王武龙，李晓楠.基于仿真反击式破碎机破碎力与冲击速度的研究［J］.矿业快报，2007，457(5):42 －45.

［8］Li Fangwei，Li Yanhuan，Xu Zhenliang，et al.Numerical simulation on the impacting and comminuting of coal based on LS-DYNA［J］.Journal of Coal Science and Engineering，2008，14(4):644－647.

［9］曾洪茂，周恩普.冲击破碎机冲击速度、冲击时间和冲击力的确定［J］.矿山机械，1994，1:2－6.

［10］秦志英，陆启韶.基于恢复系数的碰撞过程模型分析［J］.动力学与控制学报，2006，4(4):294 －298.

［11］秦志英，赵月静，侯书军.物料冲击破碎过程的一种非线性力模型［J］.振动与冲击，2006，25(2):35 －38.

［12］徐秉业.接触力学［M］.北京:高等教育出版社，1985.

［13］徐小荷，余 静.岩石破碎学［M］.北京:煤炭工业出版社，1984.