复杂曲面加工过程多约束自适应进给率控制策略

任 斐， 孙 玉 文， 郭 东 明

（1.大连理工大学 精密与特种加工教育部重点实验室，辽宁 大连 116024；2.上海航天设备制造总厂，上海 200245）

0 引 言

随着航空航天、国防和汽车制造等工业的广泛发展，很多零件因采用整体结构件而使材料的去除量显著加大，提高该类零件的加工效率受到越来越多的重视.进给率定制是影响加工过程的重要因素，进行进给率的自适应定制对改善切削状况，提高加工质量和效率具有重要的工程应用价值.

在进给率定制模型中，通常以恒定材料去除率［1～3］或恒定切削力［4～6］为目标.Eridm 等［7］分别从理论和实验方面对基于两种模型的进给率优化方法进行了比较分析，指出前一种模型能获得更大的进给率，但随之增大的切削力有可能引起刀具的变形和磨损，甚至破坏加工过程的稳定性和机床本身.目前，基于恒力的进给率定制策略［8～11］通常假定预测的切削合力与进给率呈线性关系来修正进给率，使加工过程中切削合力保持恒定，但其依据的铣削力预测模型也多以近似圆弧计算切屑厚度.此外，在进给率优化模型的约束条件中，一般主要使用刀具横向断裂强度约束峰值力［8］，或考虑切屑厚度约束对进给率的制约［9］.由于加工中自由曲面上各点切削状态的复杂性以及进给率的加大，建立在水平直线槽切基础上的刀刃运动轨迹的近似圆弧假定已受到很大的限制，针对带有倾角的平面直线加工已有相应的修正公式［12、13］，但仍不能满足任意轨迹下精确铣削力预测的要求.此外，约束条件的不全面也可能对工件加工表面误差以及刀具和机床的安全性等带来不利的影响.

为此，本文提出一种基于切削力精确预测的进给率定制模型.该模型首先基于刀具与工件的相对运动分析，建立铣削力的预测模型；在此基础上综合考虑实际加工中的各种制约因素，实现以精度、刀具应力、扭矩等约束下材料去除率最大化为目标的进给率优化定制.

1 切削力精确预测模型

1.1 铣削力模型

对于球头铣刀刀刃上任意切削微元，根据切削力与未变形切屑厚度成正比的假设，建立切向（dFt）、径向（dFr）和轴向（dFa）微元切削力公式：

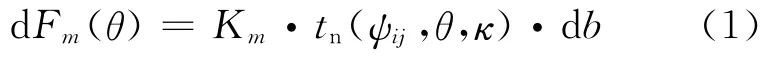
式中：m＝t，r，a；Km（MPa）表示切削力系数，可通过文献［14］所述验证方法获得；ψij表示第i个切削刃上第j个微元刀刃在刀具转角为θ时的角度，ψij（θ，z）＝θ＋2π（i－1）/N＋zj（tani0）/R0，zj表示该微元刀刃在刀具坐标系下的z坐标；tn（mm）为相应的未变形切屑厚度；db（mm）表示微元刀刃的厚度.

1.2 未变形切屑厚度

由式（1）可以看出未变形切屑厚度是影响铣削力仿真结果的重要因素之一.根据图1所示的几何关系，全局坐标系下切削微元的瞬时未变形切屑厚度可通过计算点P和Q之间的距离得到.

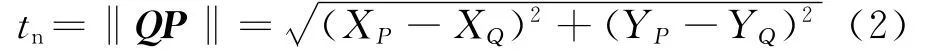
使用式（2）计算切屑厚度需解决：（1）描述P点对应的前刀刃轨迹；（2）定义线段CP.

图1 未变形切屑厚度计算示意图Fig.1 Schematic diagram of undeformed chip thickness calculation

1.2.1 任意微元刀刃的前刀刃轨迹 考虑复杂曲面加工中零件几何特征和刀具路径拓扑形状影响建立基于描述微元刀刃真实运动轨迹的切屑厚度准确计算模型.假设P点在全局坐标系下的坐标分量为XP、YP和ZP，根据文献［14］分析，前刀刃轨迹为

1.2.2CP与前刀刃轨迹的交点 设为t时刻P点的位置矢量，rcPl为相应的刀位点矢量，则CP可定义为

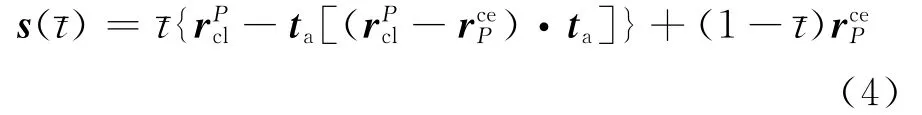
由给定的微元刀刃和式（3）、（4）可知交点满足

考虑到参数t＊和之间的隐式关系，使用数值方法求解该方程.通过迭代可解变换后前刀刃轨迹和CP的交点.当有多个交点存在时，根据文献［15］，可求出所有的交点（Q1，Q2，…），真实的未变形切屑厚度值为对应每个交点的未变形切屑厚度中的最小值

2 进给率优化模型

通过调节刀具进给率加快工件材料去除是提高加工效率的有效途径.本文基于提出的切削力精确预测模型，结合悬臂梁模型、应力模型和扭矩计算公式，分析了进给率调节过程中由切削力引起的刀具内应力、刀杆受力变形以及机床主轴扭矩的变化规律.通过约束这些影响加工过程的关键因素，在保证加工精度、刀具和机床安全的基础上，最大限度地实现高效率加工.

式中约束条件分别对应加工误差约束、刀具内应力约束和机床主轴扭矩极限.

2.1 材料去除率模型

在被加工曲面任意刀具路径的采样点处，材料去除率可由刀具进给率和行距的乘积描述：

式中：f为刀具进给率；l为给定加工误差条件下最大可行行距，

式中：［ε］为给定加工误差，κn（l）为行距方向曲面法曲率.

2.2 加工误差

刀具受力变形是曲面加工误差产生的重要原因.为保证零件加工精度，刀具变形引起的加工误差应控制在许可范围内：

2.2.1 刀具变形 基于将刀具简化为悬臂梁结构的假设对刀具受力变形进行分析.作用在切削合力位置的瞬时切削合力在刀具坐标系下分解为刀轴方向的力FcZ和刀具横截面内的力FcX和FcY.由于刀轴方向的刚度远远大于刀具横截面方向的，忽略刀轴方向的变形，只考虑刀具受FcX和FcY产生的弯曲变形.

定义瞬时切削合力对刀具在球心位置产生的变形为此刻的刀具变形：

式中：E为弹性模量；I为惯性矩；λ＝X，Y；运算法〈〉表示〈b〉＝b当b≥0，否则〈b〉＝0.

2.2.2 刀具变形引起的加工误差 在切削成形过程中，零件与刀具相互作用产生的对理论位置的偏离决定了加工误差.如图2所示，被加工曲面上点P由刀刃点B运动到理想曲面上点P＊加工生成.理想情况下，P与P＊重合，P与该时刻刀具球心点O＊间的距离为刀具半径：

但受加工参数以及刀刃几何形状影响（螺旋角不为零），B与P＊接触时，除刀刃点B之外的其他参与切削的微元产生的切削力使得刀具受力变形造成点P出现

刀刃切削后剩余材料厚度在点P＊法矢上的投影即为点P＊的加工误差：

式中：F为点P＊与其法矢构成的直线与以O为球心、R0为半径构成的球的交点.

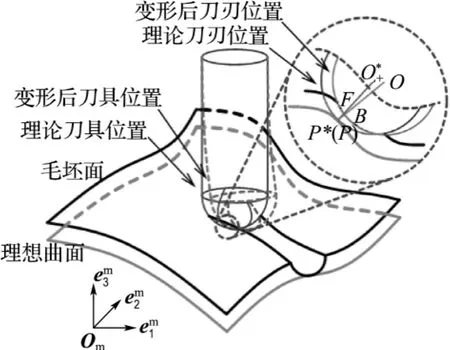
图2 由刀具变形引起的加工误差计算示意图Fig.2 Schematic diagram of establishing the machining error caused by tool deflection

2.3 刀具内应力

切削力引起的铣刀内部最大拉应力不能超过刀具材料的极限应力：

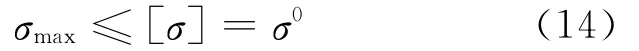
式中：σmax为刀具内部最大拉应力；σ0为刀具材料的极限应力，可由轴向拉伸实验获得.

加工中任意时刻刀具受力如图3（a）所示，在考虑轴向力拉压作用情况下，刀具横截面所受应力

式中：M x和M y为对过梁质心的x和y轴的力矩，I为惯性矩，A为刀具横截面面积.

在分析刀具横截面几何模型的基础上，给出惯性矩和横截面面积的解析计算公式.如图3（b）所示，刀具横截面区域由半径为r和rcf/2的多个圆弧构成，在△OzjBA中，根据余弦定理有

式中：Re（θ，zj）为横截面等效半径，又因为

式中：R（zj）为z＝zj截面处刀具半径，因此

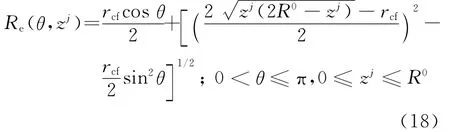
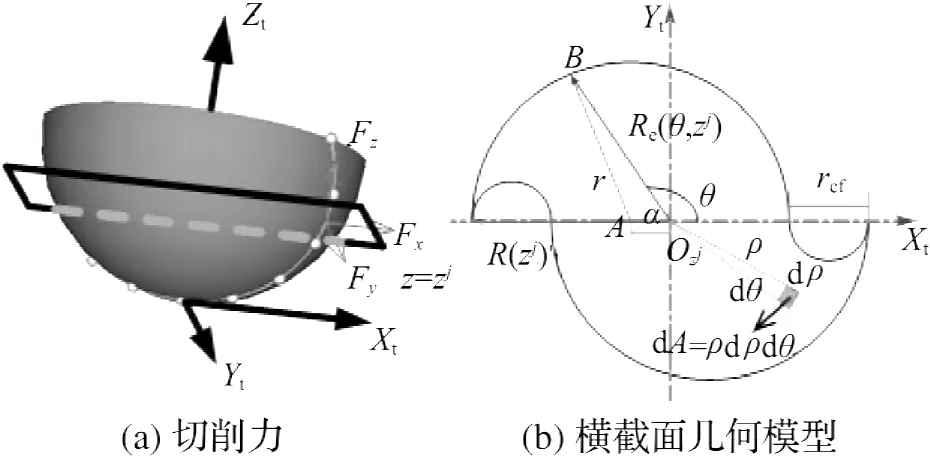
图3 内应力计算Fig.3 Calculating of the internal stress

根据定义和边界条件，可得横截面面积和惯性矩如下：

当0≤zj＜R0时

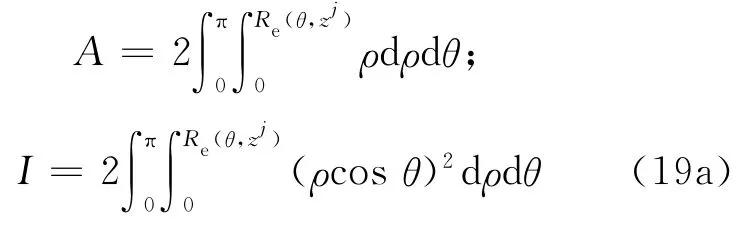
当zj≥R0时

加工中最大刀具应力通常发生在刀具横截面边界处，引入等效半径，则最大应力可表示为

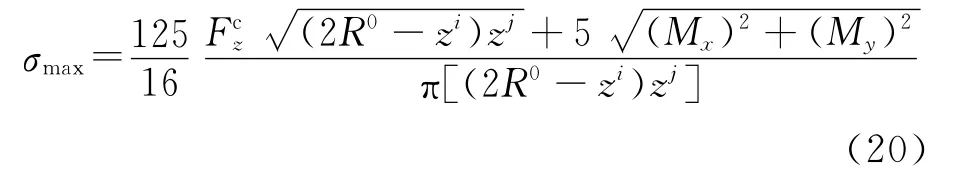
2.4 机床主轴扭矩极限

给定加工条件下，切削力产生的扭矩峰值不能超过机床主轴扭矩阈值.任意加工时刻，主轴所受扭矩Tc可表示为

式中：Ne为参与切削微元刀刃的个数；dFjt和Rj分别为刀刃微元j的切向力和半径，

对于各tr周期内 （tr＝1/S）

2.5 优化进给率计算

对于任一采样点，计算刀具转动一周内加工误差、刀具应力和机床主轴扭矩的最大值：εmax、σmax和Tcmax.计算最大值与给定阈值的比值，其中比值最大的即为当前进给率下的关键约束因素.根据关键约束因素，描述加工过程的一阶传递函数，以及比例积分控制，计算进给率的调节增量，并修正当前的进给率.使用修正的进给率重新计算约束因素峰值.整个过程循环迭代直到约束因素中的任意一个超过给定阈值.

在z域中，用一阶传递函数近似表达进给率和最大值之间的关系：

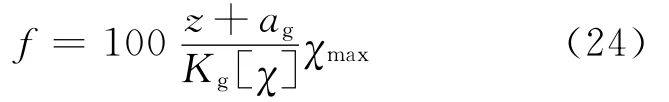
式中：χ＝ε，σ，Tc；ag＝－e－4，为固定的极点；Kg为时变增益，

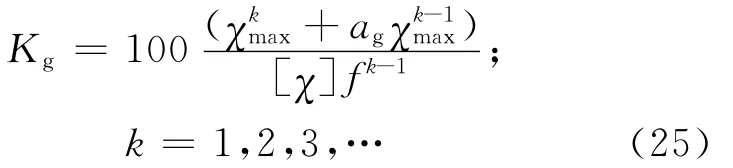
采用比例积分控制方法调节进给率

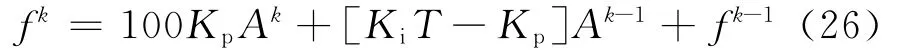
式中

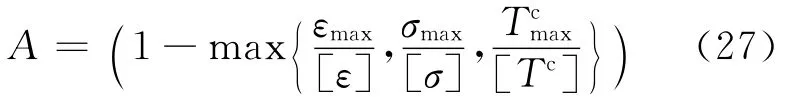
Kp、Ki、T采用文献［16］计算结果.

根据式（24）～（27）计算的进给率被写入相应NC代码中，构成优化的数控加工代码.

3 实验验证

为了验证所给模型，对图4（a）所示被加工零件以及由CAM软件UG生成的数控加工G代码程序进行自适应进给率定制.实验所用刀具为10硬质合金两刃球头铣刀，工件材料为45＃钢.设定许用加工误差εmax＝0.02 mm，刀具材料的极限应力σ0＝355 MPa，机床主轴扭矩极限Tcmax＝53 N·m.以各个代码对应的刀位点为采样点计算的刀具转动一周内加工误差、刀具应力和机床主轴扭矩的最大值见图4（b）.基于式（27）比较各个制约因素重要性，迭代计算出各个采样点对应的优化后的进给率.从表中（图4（b））可以看出，在不同采样点处制约进给率定制的因素各不相同，在采样点P14位置处，刀具应力约束起决定性作用，进给率以σ0为调节准则；在采样点P9位置处，机床主轴扭矩约束起决定性作用，进给率以为调节准则；在采样点P5和P18位置处，加工误差约束起决定性作用，进给率以εmax为调节准则.优化前后的进给率随工件长度L的变化如图4（c）所示.图4（d）给出优化前后采样点加工误差，可以看出随进给率调整加工误差增加但并未超过许用加工误差.基于优化后的数控代码，通过实际加工验证，进给率优化前加工时间约为71 s，进给率优化后加工时间仅约为38.6 s，加工效率提高45.6%.

图4 多约束进给率优化实验验证Fig.4 Verification of multi－constraints feedrate optimization model

4 结 论

本文给出了基于刀具运动分析的切削力模型和加工过程多约束的进给率定制方法.基于刀具－工件相对运动分析，推导出沿任意刀具路径拓扑形状加工复杂曲面过程中刀刃微元真实运动轨迹的解析表达，在此基础上给出了瞬时未变形切屑厚度精确计算结果，减少了使用基于刀刃运动轨迹为圆弧假设的切削力模型计算带来的误差.以刀具应力、加工误差、机床主轴扭矩为约束，给出用于进给率定制的有约束极值计算模型.通过分析球头刀横截面几何特性，给出了计算刀具变形、应力时所用到的面积、惯性矩等关键参数的解析计算公式，改善了使用等效半径计算面积和惯性矩对结果精度的影响.通过使用一阶传递函数表达加工过程，并采用比例积分控制方法实现了对进给率的调节.实例验证了该模型的可行性，在保证加工质量的同时提高了加工效率，非常适于复杂曲面高效高精度加工.

［1］WANG W P.Solid modeling for optimizing metal removal of three－dimensional NC end milling ［J］.Journal of Manufacturing Systems，1988，7（1）：57－65

［2］IP R W L，LAU H C W，CHAN F T S.An economical sculptured surface machining approach using fuzzy models and ball－nosed cutters ［J］.Journal of Materials Processing Technology，2003，138（1－3）：579－585

［3］JANG D，KIM K，JUNG J.Voxel－based virtual multiaxis machining ［J］.International Journal of Advanced Manufacturing Technology，2000，16：709－713

［4］SALAMI R，SADEGHIM H，MOTAKEF B.Feed rate optimization for 3－axis ball－end milling of sculptured surfaces ［J］.International Journal of Machine Tools and Manufacture，2007，47：760－767

［5］SUN Yu－wen，LI Dai－di，REN Fei，etal.Predictive force model based variable feedrate scheduling forhigh－efficiency NC machining ［J］.Lecture Notes in Computer Science，2008，5315：1076－1085

［6］GUZELB U，LAZOGLU I.Increasing productivity in sculpture surface machining via off－line piecewise variable feedrate scheduling based on the force system model［J］.International Journal of Machine Tools and Manufacture，2004，44：21－28

［7］ERIDM H，LAZOGLU I，OZTURK B.Feedrate scheduling strategies for free－form surfaces ［J］.International Journal of Machine Tools and Manufacture，2006，46：747－757

［8］KO J H，CHO D W.Feed rate scheduling model considering transverse rupture strength of a tool for 3D ball－end milling ［J］.International Journal of Machine Tools and Manufacture，2004，44：1047－1059

［9］BAILEY T，ELBESTAWI M A，EL－WARDANY T I，etal.Generic simulation approach for multi－axis machining，part 2：model calibration and feed rate scheduling［J］.Journal of Manufacturing Science and Engineering，Transaction of the ASME，2002，124：634－642

［10］FUSSELL B K，JERARD R B，HEMMETT J G.Robust feedrate selection for 3－axis NC machining using discrete models［J］.Journal of Manufacturing Science and Engineering，Transaction of the ASME，2001，123：214－224

［11］KARUNAKARAN K P，SHRINGI R.A solid model－based off－line adaptive controller for feed rate scheduling for milling process ［J］.Journal of Materials Processing Technology，2008，204：384－396

［12］LAMIKIZ A，LO′PEZ L N，DE LACALLE J A，etal.Cutting force estimation in sculptured surface milling［J］.International Journal of Machine Tools and Manufacture，2004，44：1511－1526

［13］IMANI B M，SADEGHI M H，ELBESTAWI M A.An improved process simulation for ball－end milling of sculptured surfaces［J］.International Journal of Machine Tools and Manufacture，1998，38：1089－1107

［14］SUN Yu－wen， REN Fei， GUO Dong－ming.Estimation and experimental validation of cutting forces in ball－end milling of sculptured surfaces［J］.International Journal of Machine Tools and Manufacture，2009，49：1238－1244

［15］SEDERBERG T W， NISHITA T. Curve intersection using Bezier clipping ［J］.Computer Aided Design，1992，22（9）：538－549

［16］FERRY W B，ALTINTAS Y.Virtual five－axis flank milling of jet engine impellers partⅡ：feed rate optimization of five－axis flank milling［J］.Journal of Manufacturing Science and Engineering，Transaction of the ASME，2008，130：011013