基于信号特征谱的地面运动目标分类

李彦兵 杜 兰 刘宏伟 徐丹蕾 关永胜

(西安电子科技大学雷达信号处理国家重点实验室,陕西 西安 710071)

1.引 言

现代战场环境中，由于不同的作战任务以及不同的环境需求，轮式车辆与履带式车辆往往承担不同任务。通常来说，轮式车辆重量轻机动性强，承担侦察或运输任务，履带式车辆重量大防御力强，承担作战任务。由于两种车辆承担任务种类的差异性，决定了其威胁程度不同，因此对战场环境中各种车辆目标进行分类在现代战争中具有重要意义。

自然界中许多物体在运动时，除了自身平动，物体上某些部件还会有相对物体的运动，称为微运动，如直升机飞行时主旋翼和尾翼的转动，车辆行进时车轮的转动等。这种运动是不同的物体所特有的，可以用来对特定目标进行探测和识别[1-3]，文献[4]利用数学模型分析了几种典型微运动形式，将微多普勒调制概念引入雷达领域。自此，对微动信息的提取以及利用微动信息对目标进行分类成为了雷达目标识别的研究热点。文献[5]基于直升机和人的实测数据利用小波变换和时频分析对微动特征进行了提取。结果表明微动特征反应了物体上非刚体运动部件的运动本质。文献[6]详细分析了人在各种步态下的微动特征，利用这些特征对人的各种步态进行了识别。这些研究成果表明，物体运动时的微动特征反应了物体的本质信息，能够用来对物体进行分类和识别。

在地面运动目标分类和识别领域，对于低分辨雷达，目标的距离像仅占一个或几个距离单元，同时目标回波中还存在杂波，因此从距离像中难以获取有利于目标分类和识别的信息。相比而言目标的多普勒信号，也即慢时间信号提供了目标自身的微动信息，并且沿慢时间维处理，可以将动目标和杂波分离，因而可以利用目标的微动特征对地面运动目标进行分类和识别。文献[7]在分析了轮式和履带式车辆多普勒谱差异的基础上，利用主分量分析(PCA)对目标的多普勒谱进行特征提取，利用提取的主分量特征使用线性判别分析(LDA)对车辆目标进行了分类。但由于目标多普勒谱主峰位置和谱展宽程度与目标平动速度密切相关，在进行PCA处理前需要对目标的速度进行对齐，增加了预处理过程，同时由平动速度变化带来的多普勒谱宽度变化也会对分类结果产生影响。本工作针对低分辨、短驻留时间条件下的地面运动目标分类问题，在分析轮式和履带式车辆微动模型的基础上，使用回波信号的特征谱对微动特征进行描述，并从特征谱中提取特征进行目标分类。

2.车轮和履带的微运动模型

目标与雷达之间有相对运动时，回波信号会产生多普勒频率

(1)

式中:λ为雷达发射信号波长;v为目标与雷达的径向相对速度。由式(1)，λ越短，多普勒频率对速度的变化越敏感。因此，为了更好的获得目标微多普勒信息，雷达通常以较短波长发射信号，也即雷达工作频率处于较高波段，如X，Ku，K，Ka波段。这种条件下，雷达波长远小于目标尺寸，目标散射特性满足光学区假设。若仅考虑目标的直接散射，则目标的雷达截面积可由多散射中心模型近似，此时雷达单天线接收到的目标微动部件的回波信号为

σjamming(t)exp[jφjamming(t)]

(2)

式中:Ak为第k个散射点的散射系数;f0为载频；τk为第k个散射点的时延；N为散射点总数；σjamming和φjamming是随机变量，分别表示干扰的功率和相位。经过混频后，得到的回波信号可以表示为

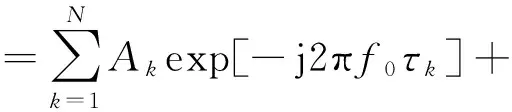
σjamming(t)exp[jφjamming(t)]

(3)

(4)

式中：R0为目标到雷达的径向距离；c为电磁波传播速度。将式(4)带入式(3)可得

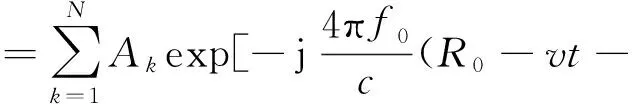
(5)

由式(5)可以看出，目标微动部件回波的相位由三部分组成，分别为由距离产生的相位、由平动速度产生的相位和由微动速度产生的相位。其中，由距离R0产生的相位为常数，分析时可以不考虑。假设目标的平动速度已经被补偿且干扰已经被抑制，下面建立目标微动部件的回波模型。首先考虑单散射点P转动的情况，设散射点转动半径为r0，角频率为ω，初始转角为θ0.则散射点P的微运动回波信号可以表示为

s(t)=Aexp[-jβsin(ωt+θ0)]

(6)

式中：A为散射点散射系数；β=4πf0r0/c=4πr0/λ，λ为雷达发射信号的波长。

式(6)可以使用傅里叶级数展开，有

(7)

式(7)中的傅里叶系数为

(8)

其中Jn为第一类n阶贝塞尔函数。

将式(8)带入式(7)可以得到转动单散射点P的微动回波信号形式

(9)

其次考虑多散射点的情况。对于车轮，如图1所示，假设有N个散射点均匀分布在圆周上，则N个散射点将有N个不同的初始转角。第k个散射点的初始转角可以表示为

θk=θ0+2π(k-1)/N

(10)

式中k=1,2,…，N.此时N个散射点的微动回波信号可以表示为

(11)

对于履带，如图2所示，其微运动部分的回波信号应为当散射点P分别位于AB、BC、CD、DA段所产生的微动回波之和。当P位于AB和CD段时，微运动为转动，CD段回波相对于AB段回波还附加一个由履带长度b带来的相位项。当P位于BC和DA段时，微运动为平动。由以上分析可知履带总的微动回波信号为

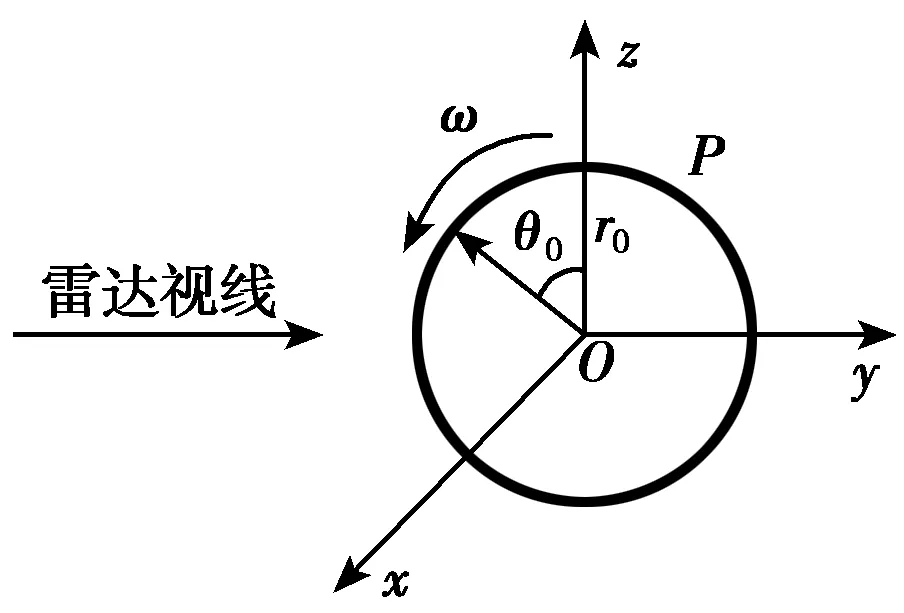
图1 车轮运动示意图

图2 履带运动示意图

s(t)=sAB(t)+sBC(t)+sCD(t)+sDA(t)

(12)

式中：N1，N2，N3，N4分别为AB，BC，CD，DA段的散射点数，假设各段上的散射点均匀分布，θk为不同散射点的初始转角：

θk=θ0+π(k-1)/Nm

(13)

其中：当散射点位于AB段时m=1，k=1,2,…,N1；当散射点位于CD段时m=3，k=1,2,…,N3；yk为不同散射点的初始位置：

yk=(k-1)b/Nm

(14)

其中，当散射点位于BC段时m=2，k=1,2,…,N2，当散射点位于DA段时m=4，k=1,2,…,N4.

式(12)中第一项和第三项表示履带AB段和CD段回波，第二项和第四项表示履带BC段和DA段回波。当平动速度为v时，履带BC段和DA段分别在0和2v处产生微多普勒调制。

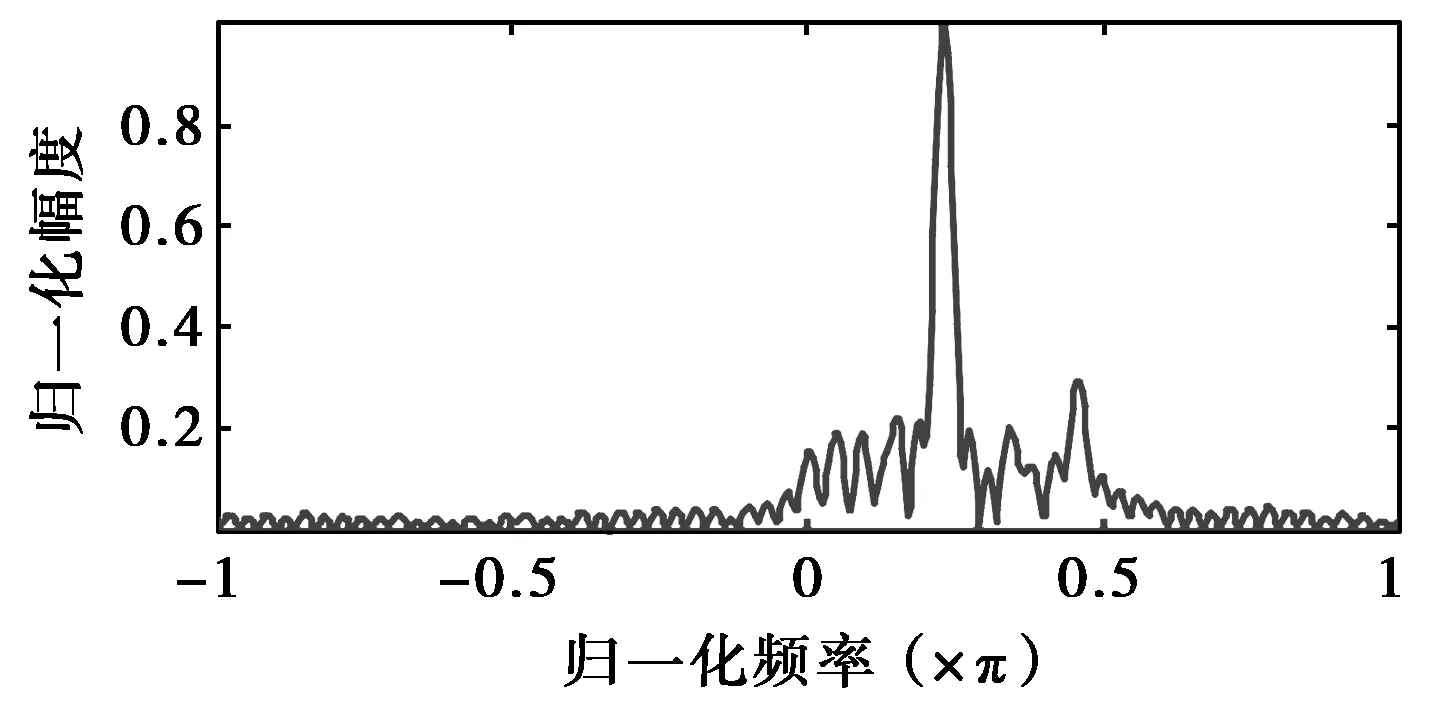
图3给出卡车和坦克未进行杂波抑制的实测多普勒谱。图中，多普勒谱的峰值频率对应目标的平动速度v。从图3可以看出，在实际中，由于轮胎的材质为橡胶，使得车轮对雷达照射信号能量的后向

(a) 轮式车辆

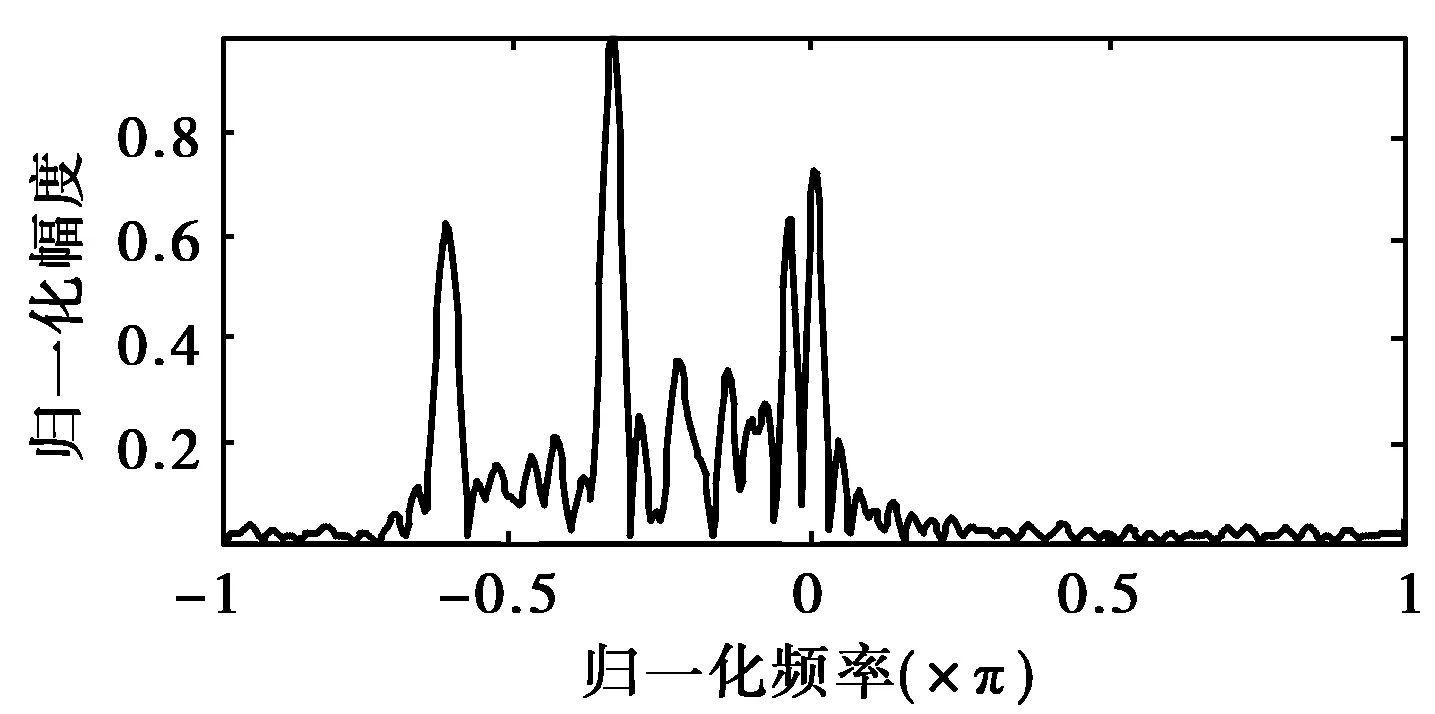
(b) 履带式车辆图3 车辆的实测多普勒谱

散射作用较小，微多普勒调制很难被观测到，因此轮式车辆多普勒谱成分简单，主要为平动多普勒成分，微多普勒成分不明显。而金属材质的履带的微多普勒调制较为明显，除平动多普勒成分外，在2v处以及0和2v之间均有微多普勒成分。对于轮式车辆和履带式车辆实测数据的多普勒谱的成分组成，文献[7]中的实测数据给出了类似结论。

3.基于特征谱的车辆目标分类

3.1 杂波抑制

地面运动目标的雷达回波信号中通常含有地物杂波。由于杂波并不包含目标自身信息，所以在对目标进行分类时，杂波成分是无用的，需要对其进行抑制。CLEAN算法可以从信号中去除特定的单频成分[8]，若在一定频带范围内多次使用CLEAN算法，则可以去除一定带宽的频率成分。因此，利用CLEAN算法可以对零频率附近的杂波成分进行抑制,其中杂波的谱宽可以由先验信息获得。使用CLEAN算法去除杂波前后的效果如图4所示。

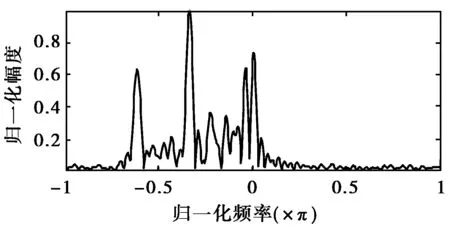
(a) 未去杂波

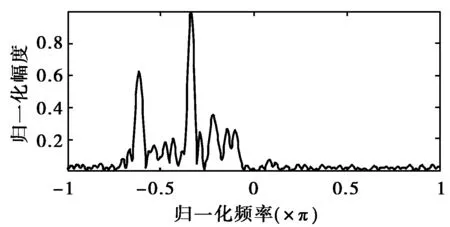
(b) CLEAN去杂波图4 CLEAN算法去除杂波前后对比

3.2 特征提取

由第二部分分析可知，实际中轮式车辆与履带式车辆微多普勒调制存在差异，轮式车辆微多普勒调制不明显，多普勒谱近似为由平动引起的单频分量。履带式车辆微多普勒调制现象明显，多普勒谱由平动和微动引起的频率成分共同构成。由式(11)和式(12)，车辆目标回波可以表示成谐波叠加形式，且轮式车辆和履带式车辆在谐波数量上存在差别，因此可以通过谐波分析的方法对车辆目标进行分类。文献[9]在分析了飞机的喷气发动机调制(JEM)现象的基础上指出，对于短驻留时间雷达，由于在一次相关处理间隔(CPI)中得到的脉冲数不足以包含一个转动周期，精确地估计谱间间隔是不易实现的，甚至连多谱勒谱宽也是难于估计的。但谐波数却是一个较为稳定的特征，并且可以通过信号的特征谱来描述。文献[9]还进一步指出，即便是在信号长度L小于谐波数M的情况下，提取的信号特征谱与理想情况下特征谱形状依然是近似的。由此可见，信号的特征谱是一个能够反应目标微动本质的较为稳定的特征。

信号的特征谱通过如下步骤获得：

1) 对长度为L的时域信号，滑窗得到L-W+1个长度为W的信号：X=[x1x2…xL-W+1]，其中，W为窗长，`也即特征谱维数；

2) 计算X的自相关矩阵：RX=XXH；

3) 对RX进行特征值分解，得到RX的特征值向量α，即为信号的特征谱。

图5给出轮式车辆和履带式车辆实测数据多次回波信号的特征谱。可以看出，特征谱反映出了轮式车辆和履带式车辆的差异，轮式车辆谐波成分较少，相应大特征值的个数较少；对于履带式车辆谐波成分较多，相应的大特征值个数较多。特征谱的最大特征值对应平动速度产生的频率成分。对于地面运动目标分类，特征谱相对于多普勒谱有两点优势：特征谱反映的是目标信号中的谐波个数，目标的平动速度的大小对于特征谱的分布并无影响，而对于多普勒谱，不同的平动速度会带来多普勒谱峰值位置的变化； 特征谱反映的是目标信号中各次谐波的能量相对大小关系，由目标平动速度不同导致的多普勒谱展宽现象对于特征谱分布也无影响。

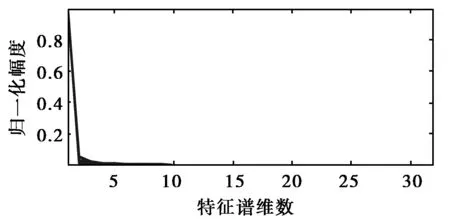
(a) 轮式车辆

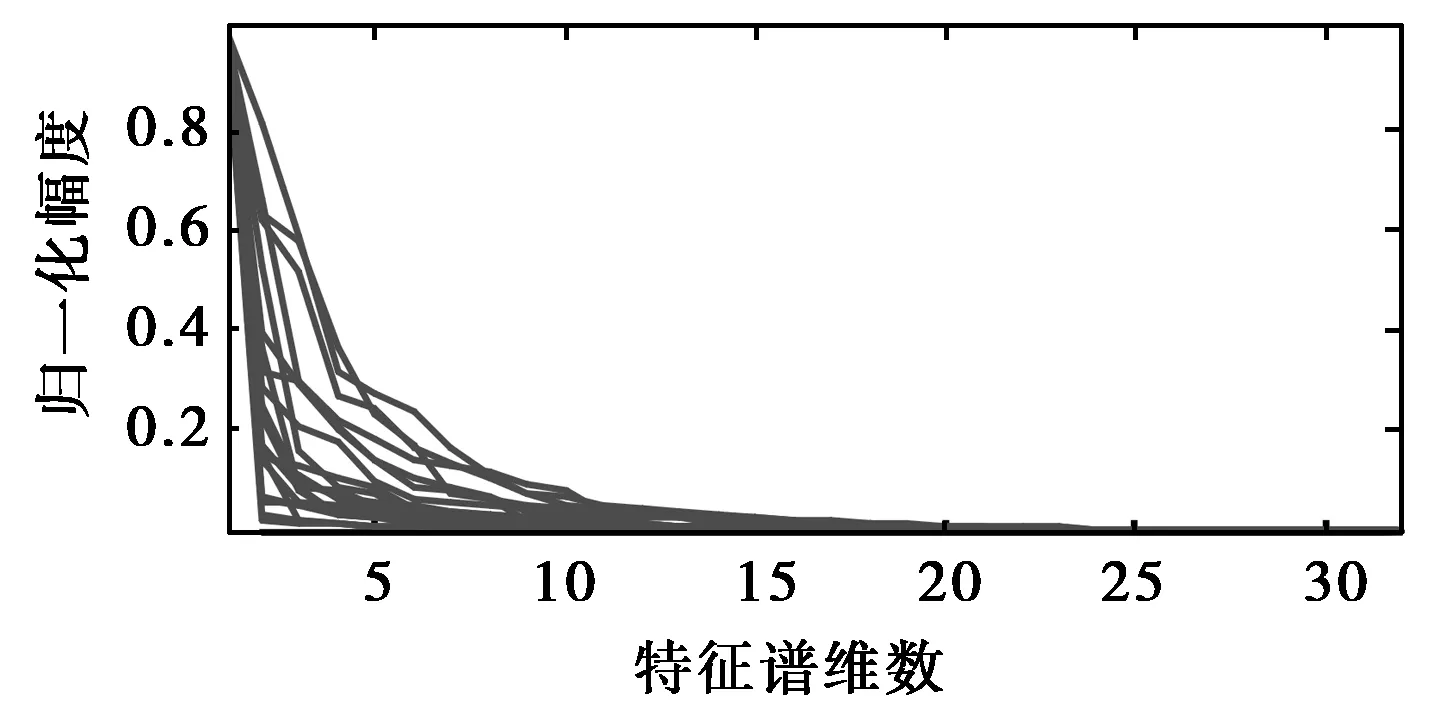
(b) 履带式车辆图5 车辆目标特征谱分布

得到了信号的特征谱后，可以直接使用特征谱作为特征向量进行分类，也可以提取描述特征谱散布程度的特征，设特征谱α=[α1，α2，…,αW]，α1≥α2≥…≥αW，对特征谱提取三种特征，分别为：

第1种：最大特征值贡献率

(15)

第2种：累积贡献率达98%时的大特征值数

(16)

第3种：最大特征值归一化后的特征值和

(17)

4.实验结果

4.1 仿真数据实验

实验首先使用仿真数据验证文中所提方法的有效性，仿真数据依据第2节建立的轮式和履带式模型产生，仿真中雷达参数如表1所示。

仿真中产生2种轮式车辆和2种履带式车辆数据，训练数据集使用其中1种轮式和1种履带式车辆数据，测试数据集使用与训练集不同车辆的数据，仿真使用的车辆目标参数如表2所示， 训练集中的车辆速度与测试集中的车辆速度有所差异，以验证在不同目标平动速度下，所提方法的有效性。仿真实验中，训练数据不加入噪声，测试数据按照不同信噪比(SNR)加入高斯白噪声评估分类性能。其中，对于每一个信噪比水平，均按蒙特卡罗(Monte-Carlo)方法加入高斯白噪声进行多次实验，实验使用支持向量机(SVM)作为分类器，SVM的核函数使用高斯核[10]，对高斯核参数进行寻优后，得到的分类性能随信噪比的变化如图6所示。图中特征谱是指直接使用特征谱作为特征向量进行分类，散布特征是指使用3.2节提出的三种特征进行分类。

表1 仿真实验的雷达参数

表2 仿真实验的目标参数

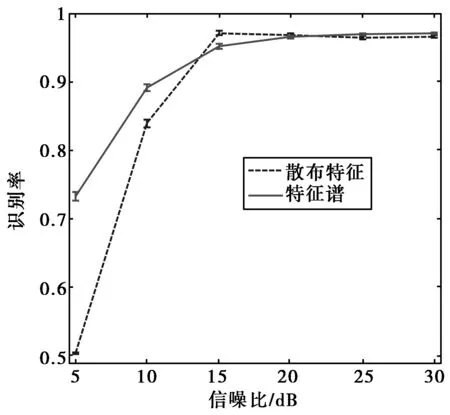
图6 仿真数据分类性能随信噪比的变化

对于每一个信噪比水平，图6给出使用特征谱和散布特征两种方式进行多次实验的平均识别率及其标准差。在信噪比为5 dB时，特征谱的识别率较差，而散布特征基本不具有分类能力；当信噪比由5 dB增至10 dB时，识别率有较大提升；当信噪比高于15 dB时，识别率较高且趋于稳定。由于微多普勒成分包含了目标微动结构的重要信息，而微多普勒成分在目标回波中所占比重相对于平动成分要小，在低信噪比情况下(SNR=5 dB)，微动信息被噪声污染，因此导致特征谱分类性能较差，而散布特征是描述特征谱局部信息的特征，在低信噪比时(SNR=5 dB)，微动信息被噪声污染，小特征值不是由微多普勒而是由噪声功率决定，因此导致散布特征不具有分类能力。同时，在5 dB至15 dB之间，不论是散布特征还是特征谱，相对于信噪比高于15 dB的情况其分类结果的标准差均较大，这是由于在信噪比较低时，微动信息受噪声影响较大，因此分类结果不稳定；相比之下，在信噪比较高时，微动信息受噪声影响较小，分类结果较为稳定。由仿真实验可以看出，使用特征谱方法对运动车辆目标进行分类时，适用于高信噪比情况，且分类结果对目标的速度变化是稳健的。

4.2 实测数据实验

接下来使用雷达实测数据验证所提方法的性能。实测场景中，雷达目标包括1种轮式车辆和2种履带式车辆，分别为卡车、坦克和装甲车。1个CPI中得到的脉冲积累数为64。训练数据集和测试数据集分别取自不同的时间段，训练数据涵盖了测试数据中的逼近和远离两种目标姿态，仅在录取时的环境上存在微小差异。为了测试算法对目标速度的稳健性，训练样本中的目标速度与测试样本中的目标速度处于不同范围，如表3所示。实验安排如下：首先评估识别率随窗长W，即特征谱维数的变化，其次给出所提方法与基于主分量分析(PCA)方法的对比，最后评估不同信噪比条件下的分类性能。实验选用SVM分类器，核函数选择高斯核函数。在实验中，每次从训练数据集中选取不同子集作为训练样本，用测试数据集进行测试，同时对核参数进行寻优。后面给出这样多次实验的平均结果。

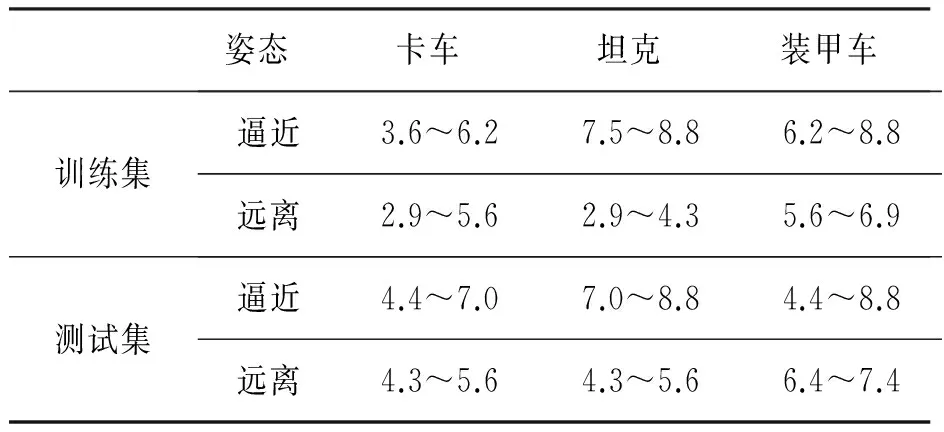
表3 实测数据集中3种车辆的速度范围/(m/s)

图7给出当信号长度为64时，识别率随特征谱维数即窗长W的变化。可以看出，识别率随着特征谱维数的变化是比较稳定的。这是因为，当特征谱维数减小时，低维的特征谱相当于高维特征谱的“采样”，它们具有相似的形状[9]。低维特征谱与高维特征谱同样反应了目标本身的微动信息，因此，使用特征谱进行分类的分类性能对于特征谱的维数具有稳健性。

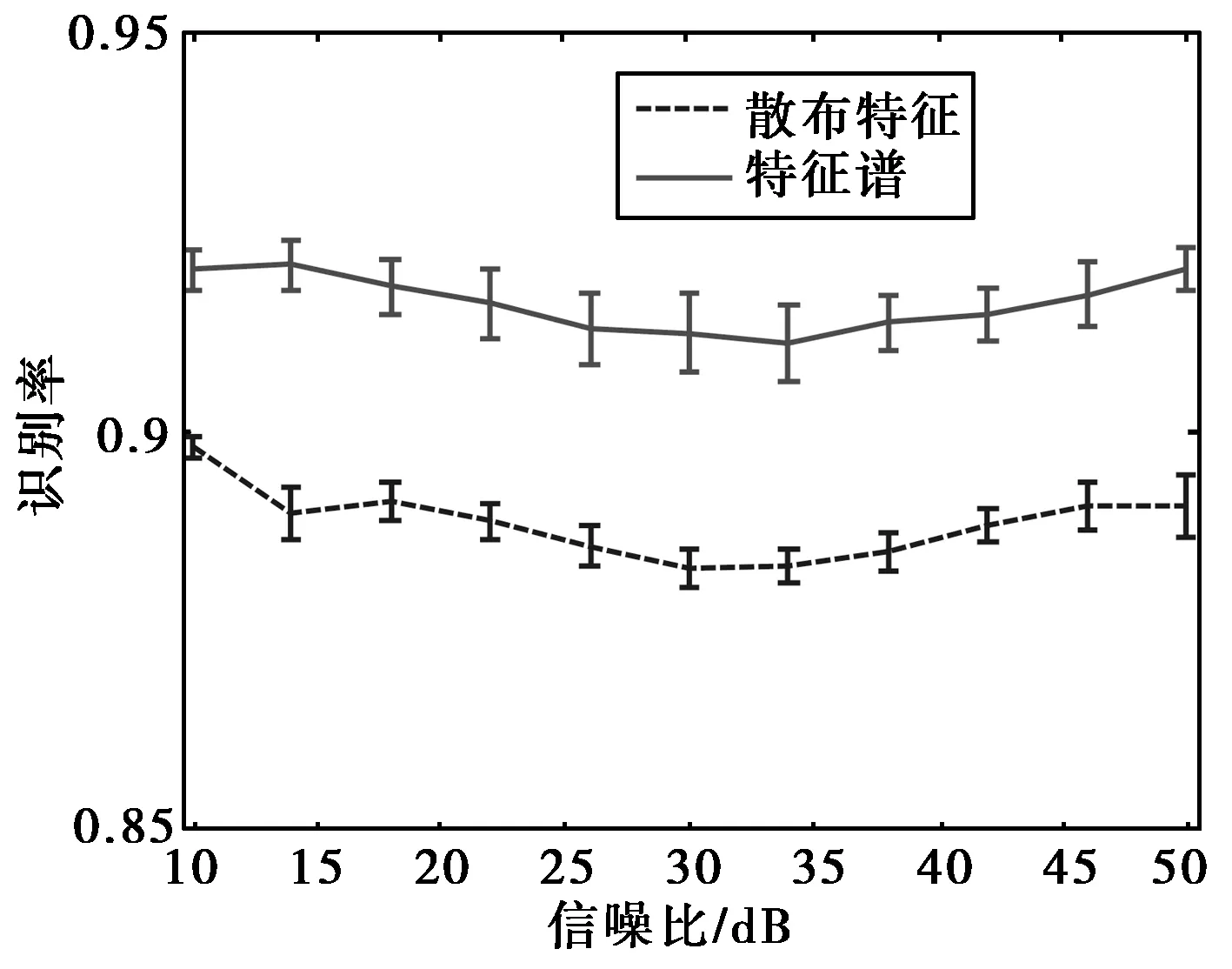
图7 分类性能随特征谱维数的变化

表4给出了当信号长度为64，特征谱维数为32时，所提方法与文献[7]中使用的PCA+LDA方法的分类结果对比，同时表4还给出了将文献[7]所提方法中的LDA换为SVM的分类结果作为对比。对于车辆目标的分类，文献[7]中使用PCA对目标多普勒谱进行降维，使用降维后的主分量对车辆目标进行分类，由于文献[7]中并没有给出主分量个数的选择方法，因此我们按照当PCA中大特征值的贡献率分别为90%，95%和98%时所对应的特征值数作为主分量个数进行实验。

从表4中可以看出，基于特征谱的分类结果优于PCA+SVM和PCA+LDA。由第2部分的分析可知，当平动速度为v时，车辆目标多普勒谱中的微动成分分布在0到2v之间，这是由车辆的结构决定的。因此，多普勒谱平动速度的变化对地面运动目标的多普勒谱产生两点影响：多普勒谱主峰的位置变化和多普勒谱的宽度变化。如图8所示，给出同一履带式车辆在不同平动速度下使用CLEAN算法抑制杂波后的实测多普勒谱。可以看出，平动速度的差异不仅使得多普勒谱的主峰位置发生了变化，同时使得多普勒谱的宽度发生了变化。对于基于PCA的特征提取方法，之前的速度对齐预处理可以消除多普勒谱主峰位置不同带来的影响，但无法消除平动速度带来的多普勒谱宽度不同对分类结果的影响。由3.2节分析可知，基于特征谱的特征提取方法既不存在速度对齐问题，也不受多普勒谱宽度变化的影响。因此基于特征谱的分类方法性能要优于基于PCA的分类方法。同时，从表4中还可以看出，基于PCA的分类方法，不论分类器选择LDA还是SVM，在大特征值贡献率为98%时的分类性能均比大特征值贡献率为90%和95%时有较大的提升，这说明对分类有较大贡献的微动信息分布在能量较小的主分量中，也即微动成分在目标多普勒谱中所占能量比例较小，这与上文中仿真实验结果分析一致。因此，实际中对于不同信噪比下分类性能的评估是一个重要问题。

(a) 平动速度较低

(b) 平动速度较高图8 平动速度变化对目标多普勒谱的影响

对于实测数据实验，通过对实测数据人工加入白噪声的方式评估不同信噪比下的分类性能。其中训练数据使用高信噪比数据，即使用未加噪声的数据，测试数据按Monte-Carlo方法加入不同信噪比高斯白噪声进行多次独立实验。实验中信号长度为64，特征谱维数为32，信噪比指脉冲积累前信噪比。图9给出在不同信噪比条件下的平均识别率及其标准差。可以看出，当信噪比为20 dB及以上时识别率较高，当信噪比降至15 dB以下时识别率下降较大，当信噪比降至5 dB时几乎不具有分类能力。另外，在信噪比较低时，平均识别率的标准差较大，在信噪比较高时，平均识别率的标准差较小，表明信噪比较低时分类性能受噪声影响较大，不稳定；而信噪比较高时，分类性能受噪声影响小，较为稳定。这与

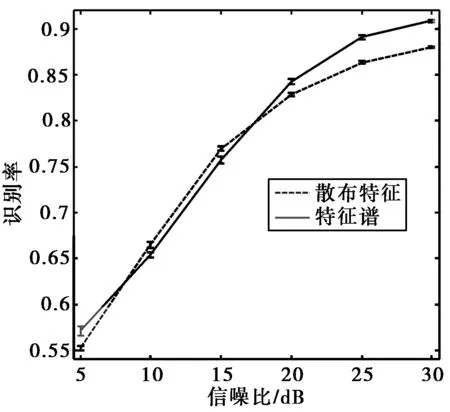
图9 分类性能随信噪比的变化

图6中所示仿真数据结果相符合。由此可得，在实际中利用目标微动特征进行地面运动目标分类时，如上文所述，目标多普勒谱的能量大多集中在平动速度引起的多普勒成分中，微多普勒成分能量相对较小。因此，在分类时要求信号具有较高信噪比，否则微动成分将被噪声污染，导致分类性能下降。

5.结 论

对于低分辨、短驻留时间雷达，从目标距离像中提取有利于地面运动目标分类的信息是比较困难的，自微多普勒概念提出后，使得人们认识到不同目标上的微动信息在一定程度上反映了目标的本质特征，为低分辨、短驻留时间雷达目标分类和识别提供了新途径。本工作利用微多普勒效应原理建立了轮式和履带式车辆的微动部件雷达回波模型，将车辆目标的雷达回波视为多次谐波成分的叠加并进一步通过对实测车辆目标多普勒谱的分析指出回波的谐波数是区分轮式车辆和履带式车辆的一个稳定特征，由此提出一种基于目标回波特征谱的特征提取方法。特征谱反映了目标回波中的谐波数量及其能量分布，且不涉及多普勒谱中平动速度成分的位置及多普勒谱的宽度，因此利用特征谱进行目标分类的结果不受目标平动速度变化的影响。需要指出，本工作所提方法利用目标的微动信息进行分类，因此要求雷达能观测到目标的微多普勒成分，对于多普勒信息无法获得的场景，如目标相对与雷达切向运动时，该方法是不适用的。

对于所提方法的性能，使用仿真数据的实验结果表明了基于特征谱的分类方法对地面运动车辆目标分类的有效性，指出在高信噪比条件下，利用目标回波的特征谱进行车辆目标分类能获得较好的分类结果；同时，使用实测数据的实验结果表明利用目标回波的特征谱进行车辆目标分类的结果对于特征谱长度具有稳健性且在地面运动车辆目标分类的应用中优于基于目标多普勒谱使用PCA进行特征提取的分类方法，并进一步验证了在高信噪比条件下，该方法具有较好的分类性能。

[1] 高红卫, 谢良贵, 文树梁, 等. 基于微多普勒特征的真假目标雷达识别研究[J]. 电波科学学报, 2008, 23(4): 775-780.

GAO Hongwei, XIE Lianggui, WEN Shuliang, et al. Research on radar target identification of warhead and decoys based on micro-Doppler signature[J]. Chinese Journal of Radio Science, 2008, 23(4): 775-780. (in Chinese)

[2] 杨立明, 曹祥玉. 直升机旋翼对回波的调制效应分析[J]. 电波科学学报, 2002, 17(1): 93-96.

YANG Liming, CAO Xiangyu. Analysis of the backscattered wave from a helicopter rotor[J]. Chinese Journal of Radio Science, 2002, 17(1): 93-96. (in Chinese)

[3] 童创明, 王光明, 张晨新, 等. 喷气发动机的JEM效应调制谱分析[J]. 电波科学学报, 1999, 14(2): 136-143.

TONG Chuangming, WANG Guangming, ZHANG Chenxin, et al. Analysis of J.E.M effect modulation spectra of jet engine[J]. Chinese Journal of Radio Science, 1999, 14(2): 136-143. (in Chinese)

[4] CHEN V C, LI F, HO S S, et al. Micro-Doppler effect in radar: phenomenon, model, and simulation study[J]. IEEE Transactions on Aerospace and Electronic System, 2006, 42(1): 2-21.

[5] THAYAPARAN T, ABROL S, RISEBOROUGH E, et al. Analysis of radar micro-Doppler signatures from experimental helicopter and human data[J]. IET Radar Sonar Navigation, 2007, 1 (4): 289-299.

[6] KIM Y, LING H. Human activity classification based on micro-Doppler signatures using a support vector machine[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(5): 1328-1337.

[7] STOVE A G. A Doppler-based target classifier using linear discriminants and principal components[C]//RTO SET Symposium on “Target Identification and Recognition Using RF Systems”. Oslo, Norway, 2004: 1-12.

[8] TSAO J, STEINBERG B D. Reduction of sidelobe and speckle artifacts in microwave imaging: the CLEAN technique[J]. IEEE Transactions on Antennas and Propagation, 1988, 36(4): 543-556.

[9] 陈 凤, 刘宏伟, 杜 兰, 等. 基于特征谱散布特征的低分辨雷达目标分类方法[J]. 中国科学: 信息科学, 2010, 2(4): 624-636.

[10] BURGES C J C. A tutorial on support vector machines for pattern recognition[J]. Data Mining and Knowledge Discovery, 1998, 2(2): 121-167.