基于优势关系的粗糙集的巷道支护方案评价体系

陈建宏，郑海力，刘振肖，杨瑞波

(中南大学 资源与安全工程学院，湖南省深部金属矿产开发与灾害控制重点实验室，湖南 长沙，410083)

建立可靠而合理的巷道支护方案评价体系不仅可以选择合理的巷道支护方案，而且可以鉴别实际巷道支护结果偏离预期结果的合理程度，分析其产生的原因，及时发现和解决支护方案的评价与优选中存在的问题。而巷道支护方案的评价与优选是一个复杂系统[1-2]，不仅要考虑支护的安全性、经济性、工期以及技术可行性等诸多因素，而且对各因素进行合理的评价分析，这对正确地评价与优选巷道支护方案也是很重要的。一直以来，巷道的支护方案的评价与选择大多是通过工程类比依靠经验确立，或者以模糊数学等数学理论进行确定[3-4]。依靠工程类比建立的巷道支护方案评价体系由于缺乏数学理论，容易产生偏差；而模糊数学对于此类影响因素较多的问题虽然有较强的建模能力，能较全面地考虑软岩支护方案选择时应该考虑的因素，但没有对方案优选的内在规律和各因素属性间的重要度进行分析，无法判断各因素属性对方案优选的影响程度，因此，建立可靠、全面、合理的方案评价体系对巷道支护方案的选择，是切实可行而又必要的。基于优势关系的粗糙集理论[5-6]是在传统粗糙集理论[7-9]的基础上，用优势关系代替不可分辨关系的粗糙集理论。它不仅综合、全面地考虑了巷道支护方案选择的影响因素，而且对影响因素中的偏好信息加以考虑，更加细致、全面。此外，在粗糙集进行方案评价与选择时进行了属性约简，简化了巷道支护方案评价选择时所应考虑的因素；同时，所产生的最优支护方案是一批最优方案，提高了方案的可选择性。在属性约简后应用灰色关联理论[10-15]对条件属性的相对重要程度进行优势分析，是一种对巷道支护方案较合理的方法。

1 巷道支护方案评价模型的建立

1.1 巷道支护方案评价体系影响因素的确定

巷道支护方案评价选择时要考虑的因素复杂，为了在对巷道支护方案进行评价优选分析时层次分明，条理清晰，可以采取分层评判的方式。各因素可以分为若干一级指标，每个一级指标之下又涵盖若干二级指标，先对子层因素进行分析，再对主层因素进行综合分析评判。

参考以往巷道支护时所考虑的影响因素，巷道支护方案评价优选时所考虑的因素可以按安全性、经济性、技术可行性以及工时消耗等若干个一级指标因素划分为相应的若干子层次，每个子层次又可涵盖若干二级指标。如安全性子层次可以按照评价安全性所要考虑的因素分成类似方案成功率、类似方案支护后巷道变形情况、应急措施以及对环境的影响等二级指标，相应地，经济性、技术可行性以及工时消耗等子层次也可以分成若干二级指标。巷道支护方案评价优选时考虑的影响因素见图1。

1.2 权数分配矩阵的建立

采用相对重要程度相关等级计算法确定巷道支护方案评价体系的各评价因素优先权重，其计算方法如表1所示。因素相对重要性比较见表2。

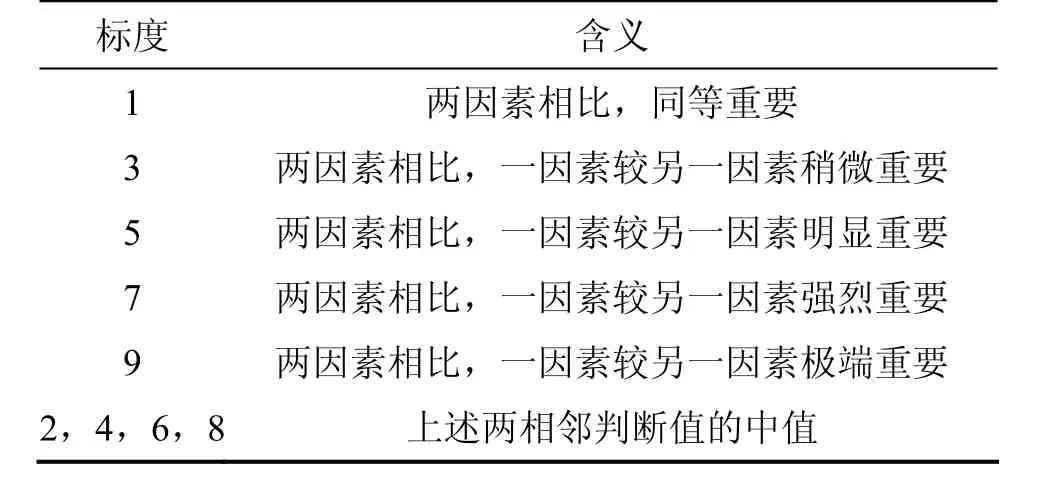
表1 相对重要程度相关等级计算法Table 1 Calculation method for relative importance level

表2 因素相对重要性比较Table 2 Relative importance comparison of factors

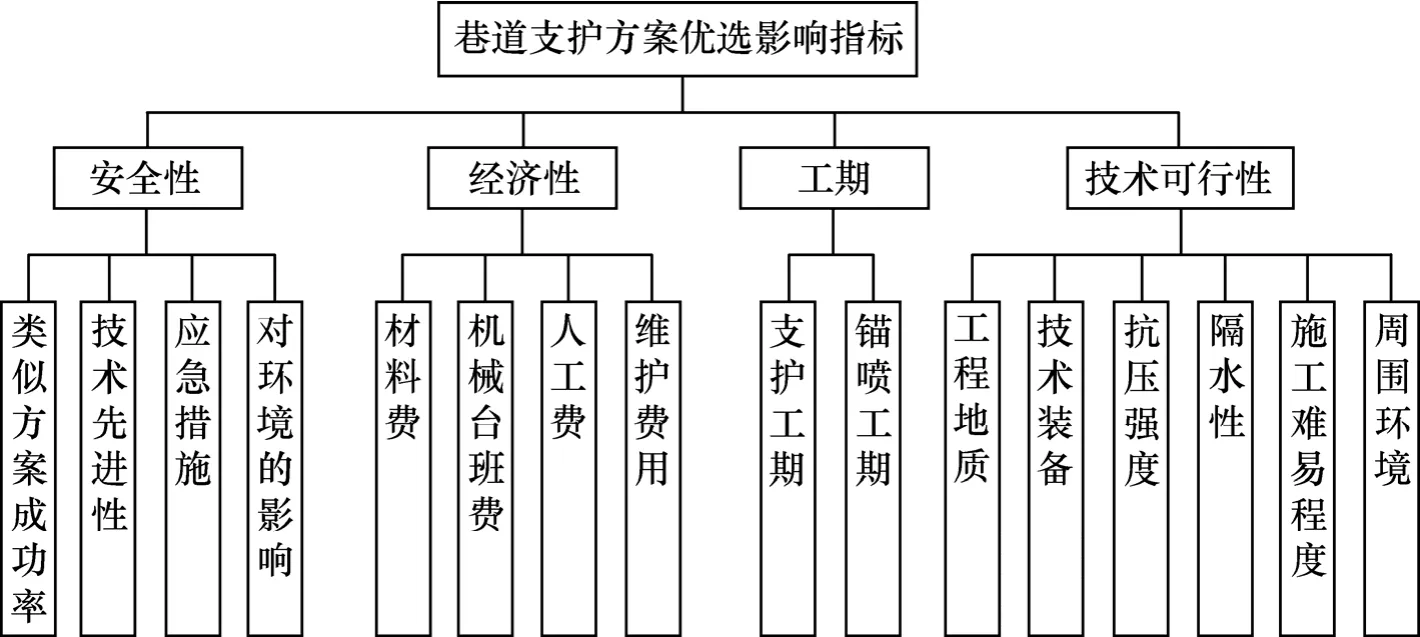
图1 巷道支护方案评价体系影响因素指标Fig.1 Influencing factors of laneway supporting schemes evaluation index system

每个因素的相对权重为：

m个因素的权重分配矩阵为：

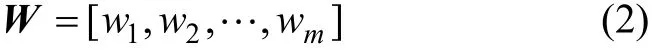
归一化处理后：

在式(1)～(3)中，i和j表示巷道支护方案评价体系中的指标因素，i=1，2，…，m；j=1，2，…，m。

1.3 评价决策表的建立

利用专家评分法对项目中所有的二级指标进行评分，并结合相应的二级指标的权重计算一级指标的分值，根据一级指标的分值及相应的权重，进一步计算各巷道支护方案的综合评分。根据专家对各巷道支护方案的评分生成巷道支护方案过程评价决策表。

1.4 数据离散

根据巷道支护方案评价指标体系的评分标准，每个指标(包括综合评价指标)都可分为优、良、中、一般、差5个级别。根据此分类级别，对巷道支护方案过程评价决策表进行数据离散，生成分级评价的偏好决策表。

1.5 约简的搜寻

对于偏好决策表中的条件属性和决策属性，这些属性包含偏好信息，即优、良、中、一般和差。按照决策属性，综合评价可分为5个偏好顺序类：Cl1={差}，Cl2={一般}，Cl3={中}，Cl4={良}，Cl5={优}。根据偏好决策类对论域进行划分，可得如下决策类的并集：

应用适当的约简算法，可搜寻到一定数量的约简，将包含属性最少且属性出现频率最多的约简视为最满意的约简，在指导巷道支护方案的评价优选时，就可以直接利用这些指标来进行，而忽略其他因素的影响。

1.6 偏好规则的生成

根据选定的约简属性生成最少偏好决策规则集D≥与D≤。

1.7 约简属性优势分析

进一步分析约简后的属性，计算各条件属性与决策属性之间的灰色关联度，对约简的条件属性集进行优势分析。基于优势关系的粗糙集理论建立的巷道支护方案评价优选模型见图2。

图2 巷道支护方案评价模型Fig.2 Evaluation model of laneway supporting schemes

2 实例分析

2.1 巷道支护方案初选

某铅锌矿的开采基本条件为：顶板为炭质泥岩，底板为砂质页岩，矿体倾角为 12°～17°，矿体平均厚度为9.3 m，围岩单向承压强度为24.6 MPa。

根据此基本条件，初步选择的巷道支护基本方案为：(1) 喷射混凝土加锚杆；(2) 喷射混凝土加钢筋网；(3) 半圆拱可缩性支架；(4) 梯形可缩性支架；(5) 梯形刚性支架。又根据各方案的支护率与所采用的支护材料的差别，将方案最终细化为n1，n2，…，n17等17种支护方案。

2.2 评价体系的建立

2.2.1 确定影响因素及相应的权重

确定的支护方案评价影响因素的一级指标有 4个：C={C1，C2，C3，C4}={安全性，经济性，工期，技术可行性}。二级指标有 16个：C={c1，c2，…，c16}={类似方案成功率，技术先进性，应急措施，对环境的影响，材料费，机械台班费，人工费，维护费用，支护工期，锚喷工期，工程地质，技术装备，抗压强度，隔水性，施工难易程度，周围环境}。一级指标与二级指标的对应关系如下。

安全性：C1={c1，c2，c3，c4}={类似方案成功率，技术先进性，应急措施，对环境的影响}；

经济性：C2={c5，c6，c7，c8}={材料费，机械台班费，人工费，维护费用}；

工期：C3={c9，c10}={支护工期，锚喷工期}；

技术可行性：C4={c11，c12，c13，c14，c15，c16}={工程地质，技术装备，抗压强度，隔水性，施工难易程度，周围环境}。

根据相对重要程度相关等级计算法，得到一级指标的权重矩阵：

W=[w1w2w3w4]=[0.19 0.37 0.11 0.33]。

各二级指标的权重确定如下：

安全性 R1=[r1r2r3r4]=[0.33 0.29 0.21 0.17 ]；

经济性R2=[r5r6r7r8]=[0.31 0.27 0.19 0.23]；

工期R3=[r9r10]=[0.57 0.43]；

技术可行性R4=[r11r12r13r14r15r16]=

[0.17 0.13 0.19 0.17 0.23 0.11]。

2.2.2 建立评价决策表

对于方案n1，应用专家评分法对安全性的二级指标评分结果为B1=[b1b2b3b4]= [88 90 85 87]。则方案n1的安全性评价指标综合得分结果为：

类似地，可以得到其他巷道支护方案的一级指标的评分结果。结合各一级指标的权重，建立起巷道支护方案评价决策表，见表3。

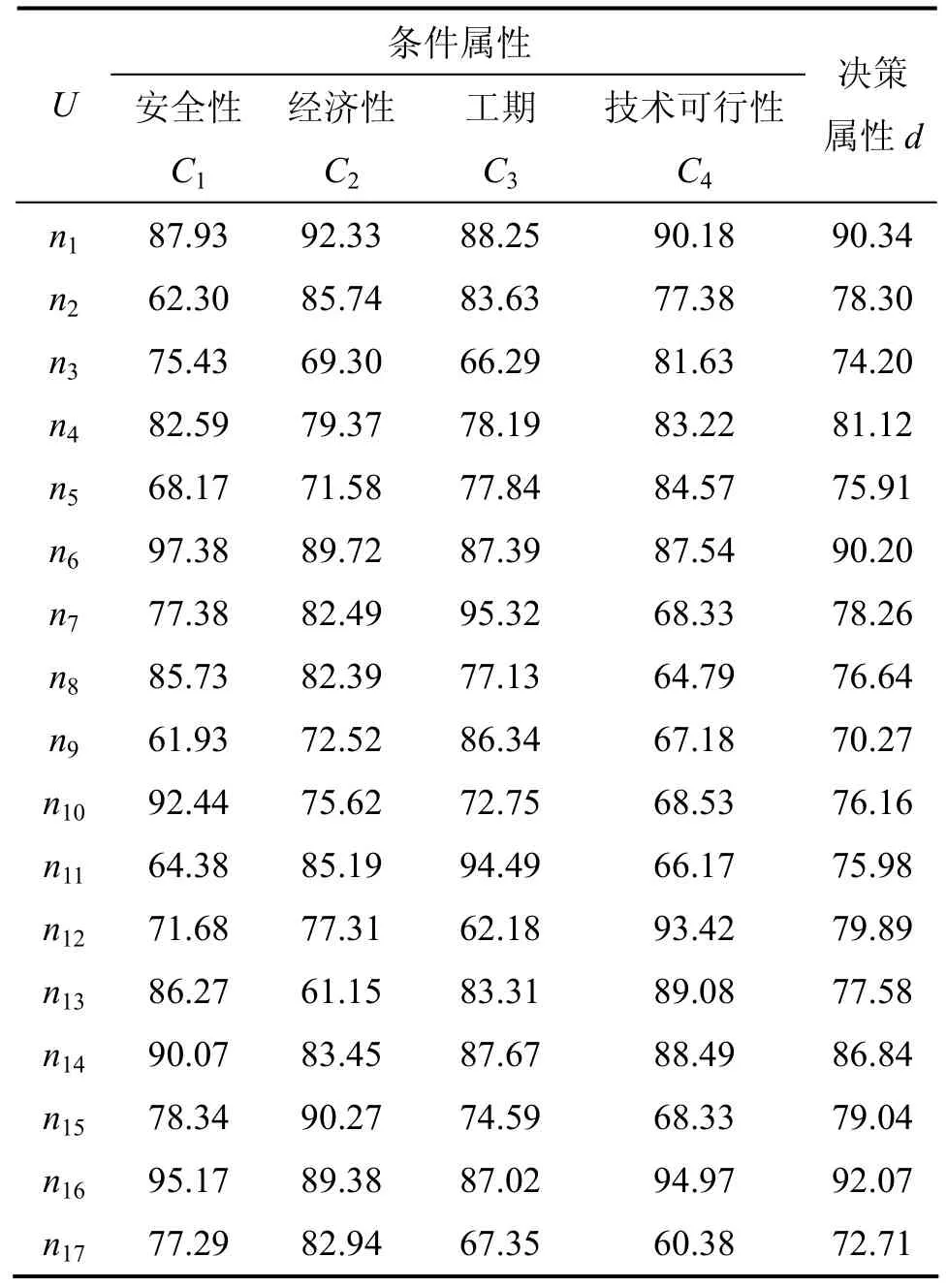
表3 巷道支护方案评价决策表Table 3 Laneway supporting schemes evaluation decision table

2.2.3 数据离散

对于评价决策表中的各个属性(包括条件属性和决策属性)的得分值，按[90，100]评为“优”，[80，90)评为“良”，[70，80)评为“中”，[60，70)评为“一般”，[0，60)评为“差”进行数据离散。得到偏好决策表，见表4。

表4 巷道支护方案偏好决策表Table 4 Preference decision-making table of laneway supporting schemes

2.2.4 约简的搜寻

对于表3中的条件属性与决策属性，显然这些属性包含偏好信息，从好到差的程度排序为优、良、中、一般。按照决策属性，综合评价可分为3个偏好顺序类：Cl1={中}，Cl2={良}，Cl3={优}。根据偏好决策类对论域进行划分，可得如下决策类的并集：

应用遗传算法进行属性约简，可搜寻到2个约简：{安全性，经济性，技术可行性}以及{安全性，经济性，工期}，可由以上约简生成偏好规则。

2.2.5 生成偏好规则集

选择约简{安全性，经济性，技术可行性}生成最少偏好规则集D≥与D≤，见表5和表6。

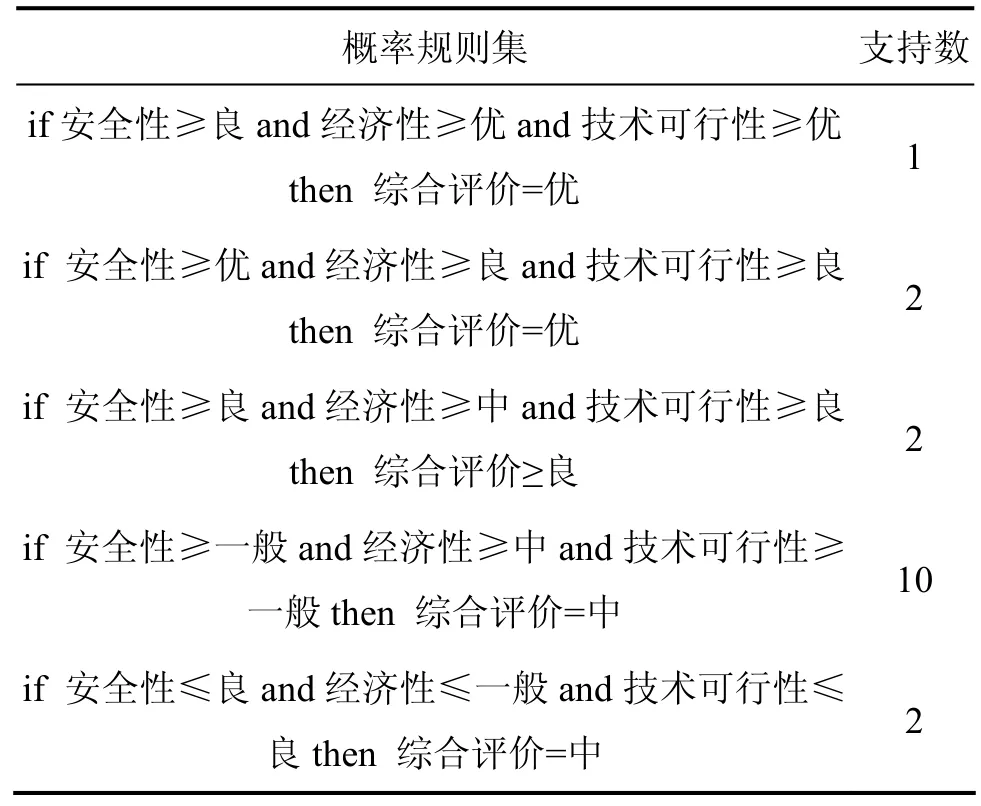
表5 D≥概率决策规则集Table 5 D≥ probability decision rules

表6 D≤概率决策规则集Table 6 D≤ probability decision rules

2.2.6 分析属性优势

以约简{安全性，经济性，技术可行性}为例，对约简后的属性进行优势分析。各序列的初值像如表 7所示。

进行始点零化像处理后，灰色关联度γ1d=0.924 4，γ2d=0.960 6，γ4d=0.965 2。γ4d＞γ2d＞γ1d，故在约简后的条件属性{安全性，经济性，技术可行性}中，针对决策属性，技术可行性＞经济性＞安全性。

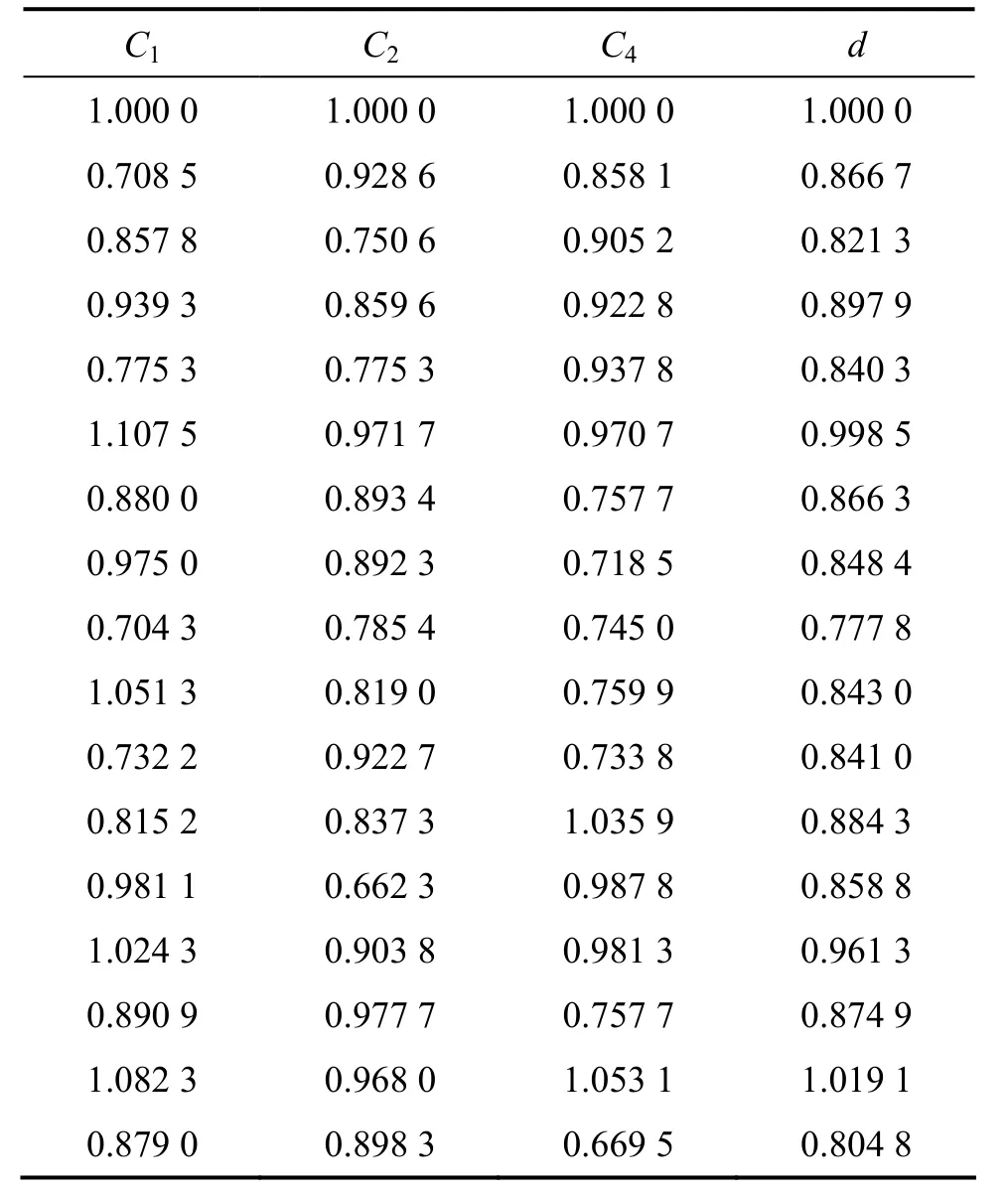
表7 序列的初值像Table 7 Series of initial value

2.3 结果分析

根据以上巷道支护方案评价体系的分析结果可知：n1，n6和 n17方案的决策属性为优，即支护方案n1，n6和n17比较适合于本矿山的巷道支护。又根据约简的结果可知：巷道支护方案的评价及选择可以用安全性、经济性及技术可行性或者安全性、经济性及工期等属性来表示，可以去掉冗余属性工期或者技术可行性。根据安全性、经济性及技术可行性生成偏好规则集时，D≥概率决策规则集的分类质量最好，达到100%，而D≤概率决策规则集的分类质量却不是很高。在对约简后的条件属性的优势分析中，技术可行性的重要程度最大，经济性的重要程度次之，而安全性不太重要。

3 结论

(1) 采用分层评判的方式建立巷道支护方案评价指标体系，将影响巷道支护方案选择的繁多复杂的因素条理化、清晰化。利用相对重要程度相关等级计算法确定各级指标的权重，并结合专家评分法建立支护方案评价决策表，减小了人为因素对方案优选的干扰。

(2) 利用灰色关联理论得出了约简后的一级指标评分值与方案评分值之间的灰色关联度，对各一级指标对方案选择影响程度以及因素属性间的重要度进行了分析。与传统的巷道支护方案优选体系相比，基于优势关系的粗糙集的巷道支护方案评价体系具有如下特点：评价体系不仅对支护方案进行了优选，而且对各影响因素与支护方案之间的关系进行了分析，考虑更加全面合理；考虑到指标因素中的偏好信息，生成了相应的偏好决策集，对各支护方案的分析更加全面和深入，并且更加符合实际情况。

(3) 利用重要程度相关等级法对各指标权重进行计算，权重计算方法科学权重构建合理。实验证明，模型可以较快地搜寻到约简，优势关系粗糙集理论可较快地对带有偏好信息的知识系统进行处理计算。

实践证明，可以将此评价体系推广应用到类似的方案评价优选中。在应用中，应注意针对具体条件合理选择方案优选的影响因素和评价指标，而且注意约简的选择。

[1] 姚宝珠. 软岩分类及软岩巷道支护方法[J]. 煤矿安全, 2003,34(12): 28-30.YAO Bao-zhu. Soft rock classification and supporting method soft failure laneway under high ground stress[J]. Journal of Coal Mine Safety, 2003, 34(12): 28-30.

[2] 李凝, 杨玉华. 软岩巷道支护技术调研[J]. 煤炭工程, 2003,34(12): 43-46.LI Ning, YANG Yu-hua. Soft failure laneway under high ground stress technology research[J]. Journal of Engineering, 2003,34(12): 43-46.

[3] 汤小凝, 李文军. 模糊决策在深基坑巷道支护中的应用[J].甘肃科技, 2008, 24(1): 112-114.TANG Xiao-ning, LI Wen-jun. The applications of fuzzy decision in deep foundation pit supporting[J]. Science of Gansu,2008, 24(1): 112-114.

[4] 勾攀峰, 汪成兵, 张道福. 巷道支护效果模糊综合评判[J]. 矿山压力与顶板管理, 2003(4): 4-8.GOU Pan-feng, WANG Cheng-bing, ZHANG Dao-fu. Effect of fuzzy comprehensive evaluation in laneway supporting[J].Journal of Mine Pressure and Roof Management, 2003(4): 4-8.

[5] 菅利荣. 面向不确定性决策的杂合粗糙集方法及其应用[M].北京: 科学出版社, 2008: 57-81.JIAN Li-rong. Facing the heterozygous uncertainty decision-making rough set method and its application[M].Beijing: Science Press, 2008: 57-81.

[6] 袁修久, 何华灿. 优势关系下的相容约简和下近似约简[J].西北工业大学学报, 2006, 24(5): 604-608.YUAN Xiu-jiu, HE Hua-can. Exploring judgment theorems and discernibility matrices useful in discovering valuable but hidden information from a certain class of decision tables[J]. Journal of Northwestern Polytechnical University, 2006, 24(5): 604-608.

[7] 张文修, 仇国芳. 基于粗糙集的不确定决策[M]. 北京: 清华大学出版社, 2005: 105-130.ZHANG Wen-xiu, QIU Guo-fang. Uncertain decision based on rough sets[M]. Beijing: Tsinghua University Press, 2005:105-130.

[8] 刘同明. 数据挖掘技术及其应用[M]. 北京: 国防工业出版社,2001: 156-188.LIU Tong-ming. Data mining technology and its application[M].Beijing: National Defense Industry Press, 2001: 156-188.

[9] 王国胤. Rough集理论与知识获取[M]. 西安: 西安交通大学出版社, 2001: 117-138.WANG Guo-yin. Rough sets theory and knowledge acquisition[M]. Xi’an: Xi’an Jiaotong University Press, 2001:117-138.

[10] 王立杰, 孙继湖. 基于灰色系统理论的煤炭需求预测模型[J].煤炭学报, 2002, 27(3): 333-336.WANG Li-jie, SUN Ji-hu. Coal required quantity forecasting based on grey system theory[J]. Journal of China Coal Society,2002, 27(3): 333-336.

[11] 张云龙, 刘茂. 灰色 GM(1,1)模型在火灾事故预测中的应用[J]. 南开大学学报: 自然科学版, 2009, 42(1): 11-15.ZHANG Yun-long, LIU Mao. Application of grey prediction model GM(1,1) in fire accident[J]. Acta Scientiarum Naturalium Universitatis Nankaiensis, 2009, 42(1): 11-15.

[12] 刘婕, 刘全稳, 徐剑良, 等. 圈闭的灰色关联分析方法研究[J].西南石油大学学报, 2007, 29(2): 72-74.LIU Jie, LIU Quan-wen, XU Jian-liang, et al. Gray correlative analysis of traps[J]. Journal of Southwest Petroleum University,2007, 29(2): 72-74.

[13] GU Hui, SONG Bi-feng. Study on effectiveness evaluation of weapon systems based on grey relational analysis and TOPSIS[J].Journal of Systems Engineering and Electronics, 2009, 20(1):106-111.

[14] XIE Nai-ming, LIU Si-feng. Research on evaluations of several grey relational models adapt to grey relational axioms[J]. Journal of Systems Engineering and Electronics, 2009, 20(2): 304-309.

[15] 刘思峰, 郭天榜, 党耀国, 等. 灰色系统理论及其应用[M].北京: 科学出版社, 1999: 174-194.LIU Si-feng, GUO Tian-bang, DANG Yao-guo, et al. The grey system theory and its application[M]. Beijing: Science Press,1999: 174-194.