摆线齿轮误差的测量及修形量计算
2011-05-10郭敬滨刘海军
郭敬滨,王 娴,刘海军,李 真
(天津大学精密测试技术及仪器国家重点实验室,天津 300072)
摆线针轮行星传动具有运转平稳、传动力矩大、单级减速比大等特点,被广泛应用于石油、机械、轻工、食品、航空及国防等工业.摆线齿轮是摆线齿轮泵和摆线齿轮减速机中的关键零件,而摆线齿轮的修形量(包括移距、等距)是影响摆线减速机性能的重要参数.如何选择这些参数、测出这些参数,成为人们最关心的问题.摆线齿轮的检测不仅是为了测量摆线齿轮的齿形误差,更重要的是为了获得实际修形参数及判断摆线齿轮加工时由于机床调整不当而产生的加工误差.为了对摆线齿轮的全齿廓误差进行测量及对修形量进行求解,笔者以极坐标测量原理为理论基础,研究摆线齿轮的极坐标跟踪测量技术及修形量参数的计算方法.
1 测量方法
摆线齿轮从齿廓曲线的生成方式来看,其齿形曲线类似于多凸轮曲线,且为直齿齿轮.测量摆线齿轮齿形误差可采用的方法有展成法、坐标法和啮合法[1-2].由于摆线齿廓曲线的形成参数较多,用展成法测量和用啮合法测量仪器结构都较复杂.而采用计算机控制的坐标测量系统比较容易实现齿形误差的测量.采用坐标测量时常用的有直角坐标系和极坐标系.采用直角坐标系测量时,测头运动行程一般相对较大,且每测一点,测头都经历退让、移到避障点、移动下一点、探测等步骤;而采用带有转台的极坐标系统,不仅测头的运动简单(测头只需要沿工件的径向作直线运动)、测量效率较高,且仅把摆线齿形看作是平面曲线,而其生成参数体现在数学模型中,这样就容易解决摆线齿轮误差的测量问题,其测量原理如图 1所示.为了满足实时跟踪的需要,该仪器采用基于数字信号处理器(digital signal processor,DSP)和现场可编程门阵列(field-programmable gate array,FPGA)的数据采集和控制系统[3].利用该测量技术可以对摆线齿轮的齿廓进行高效率、连续自动跟踪测量,以实现对摆线齿轮误差的综合测量和评定.

图1 跟踪测量系统原理Fig.1 Tracking and measuring system diagram
2 总体测量方案
采用图 1所示的测量原理测量时,其测球中心Mi的极坐标值()及测量压力角αi计算式为[4]

式中:rp为针齿中心分布圆半径;zc为摆线轮齿数;zp为针轮齿数;rQ为测头球半径;rrp为针齿半径;K1= a / rg为短幅系数,a为偏心距,rg为滚圆半径;φHp为啮合相位角.
根据摆线齿轮的极坐标方程,若采用在某一转角iφ下,直接测量在该转角下极径iρ的测量方法,将会使整个测量链缩短,易于保证测量精度,仪器结构也相对简单.为此,采用带有圆光栅的精密转台、直线电机、球形测头及测微装置等构建测量机构.将被测摆线齿轮安装在转台上,球形测头和测微装置安装在直线电机的移动座上,将直线电机自身的长光栅和导轨作为极坐标测量系统的径向基准,而角度基准为精密转台上的圆光栅.图 2为摆线齿轮测量装置的实物照片.

图2 测量装置实物照片Fig.2 Measuring device in-kind photo
采用图2所示装置进行跟踪测量时,控制系统按采样点(φi,ρi) 同时控制转台和直线电机运动,即摆线齿轮随转台旋转的同时,控制系统按极径ρi发出移动命令,控制测头向理想测量点(φi,ρi)处移动.当被测齿轮旋转到采样角度φi时,测头也同时移动到点ρi的位置.当圆光栅的计数值到达采样值,即被测摆线齿轮旋转到采样角时,系统发出采样信号,采集长光栅和测微装置的示值.
采用上述跟踪测量方案是为了减小测球磨损,并能防止测头在运动中被卡死.在图 2所示的微动装置中,在其内部弹性机构的作用下,球形测头将以一定的压力作用于旋转运动的齿面上.由于被测齿廓与测球之间有相对运动,将造成测球的磨损,影响测量精度.为提高测量精度、减小测球的磨损,在测量过程中,测头不依靠测头与齿廓接触点的径向分力推动移动(由于齿轮的旋转,在测头与齿廓的接触点将产生径向分力),而是由直线电机控制测头主动向采样点运动,这样,使测头与齿廓之间的接触力减小,可在很大程度上避免(或减小)测球磨损.
3 跟踪测量中采样方式的确定
为了便于进行误差分析及对修形量进行谱分析,测量时采用等啮合相位角方式进行采样.啮合相位角就是生成摆线时,滚圆相对于基圆的转角.啮合相位角由0°转到360°,生成一个齿廓的理论短幅外摆线;而摆线齿轮的齿廓是理论短幅外摆线的等距曲线.啮合相位角能表征摆线齿廓与针齿的啮合位置,所以,用等啮合相位角发采样信号比较合理.采用等啮合相位角采样时,其测量点在齿廓上的分布情况如图3所示.

图3 等啮合相位角Hpφ采样点分布情况Fig.3 Distribution of sampling points for interval epi- cycloid occurring-angleHpφ
从图3中可以看出,采样点在齿廓上的分布不均匀,从齿根到齿顶的采样过程中,测量点逐渐由疏变密,然后又由密变疏到齿根.对摆线齿轮来说,齿根、齿顶一般不参与啮合,齿廓中部对传动起主要作用.按照等啮合相位角采样,在齿廓中部的采样点较密,可以更好地反映齿轮的误差情况.所以,实验采用等啮合相位角采样,每一齿的采样点数 N = 3 6.
采用等啮合相位角φHp方式测量时,首先将参变量φHpi(i= 1 ,2,3,…)的值代入式(1),计算对应各个采样点的极角φi和极径ρi值.为实现跟踪测量,系统将根据采样点的极角φi和极径ρi值调整控制参数,使转台的旋转与直线电机的运动速度匹配.总之,测量过程中,转台连续转动,系统控制直线电机向采样点运动.对圆光栅进行连续计数,当计数值和采样点的极角值相等时,发出采样信号,采集长光栅、圆光栅和电感测头的值;长光栅和电感测头的值之和即为被测点所对应的极径值.直线电机继续向下一个采样点运动,直到旋转一周采集完整个齿廓上的点.根据这些值就可以算出齿轮各项误差值.
4 摆线齿轮的修形方法
摆线齿轮与其他齿轮一样,在啮合运转过程中,由于一些不可避免的制造误差(齿距偏差、齿形偏差、偏心误差等)、热膨胀及弹性变形等原因,常有发生齿形干涉的可能,有了齿侧间隙,就能有效地防止上述情况的发生.为了在传动中形成啮合侧隙,在加工中就要将摆线齿轮的齿厚减薄.摆线齿轮齿厚减薄是靠改变生成短幅外摆线等距曲线的参数来进行的.但齿厚减薄后,齿廓曲线就偏离了理论的短幅外摆线的等距曲线.通常把这种齿形称为修正齿形,或称为设计齿形.加工修正齿形的方法称为齿形修正法[5].在展成法加工中,通常采用的修正方法有移距修形法和等距修形法.
移距修形法在径向方向的修形量相同,但是法线方向的修形量不一样,在齿顶和齿根处的修形量大些,在齿廓中部的修形量小些,如图4所示.
等距修形使得齿廓在法线方向的修形量相同.为了使摆线齿轮齿顶、齿根部位的修形量大于齿侧面的修形量,采用“负移距加正等距”的修形方法.正等距修形是将加工用的砂轮圆弧半径(相当于针齿半径)加大,负移距修形是将砂轮向齿坯的中心方向移动.这样摆线齿轮与针齿轮啮合时,齿顶、齿根部位既有啮合侧隙,同时也不会发生干涉,有利于摆线齿轮的传动,如图5所示.

图4 移距修形法Fig.4 Moved distance modification method

图5 等距修形法Fig.5 Equidistance modification method
5 用傅里叶变换法求解摆线齿轮的修形量
摆线齿轮的检测不仅是为了测量摆线齿轮的齿形误差,更重要的是为了获得实际修形参数及判断加工时由于机床调整不当产生的调整误差.把实际齿廓曲线修形量称为实际作用值.由于等距修形和砂轮圆弧半径修整误差对齿侧间隙的形成及对齿廓法向误差的影响相似,为了便于分析,将两者统称为等效等距修形,用Δrrp表示.将移距修形和砂轮沿齿坯径向进给误差统称为等效移距修形,用Δrp表示.现采用傅里叶变换的方法求修形量的作用值[6-7].此值与设计者给定的修形量之差即为机床调整误差.
摆线齿轮齿廓的法向误差主要由等效等距修形、等效移距修形、偏心距调整误差和机床传动链误差引起.文献[6]利用傅里叶变换的方法,求解了摆线齿轮修形量.但经过理论分析发现,误差传递系数在频域对摆线齿轮齿廓法向误差的影响是周期性的,并且均为偶函数,其傅里叶级数的初相位为零,这些误差传递系数见表1,Krrp、Krp、Ka分别为等距修形、移距修形和偏心距引起的误差系数.
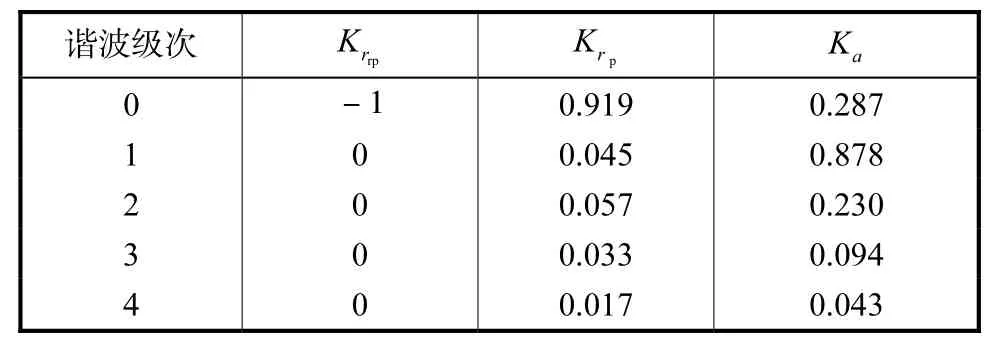
表1 各次谐波幅值的误差传递系数Tab.1 Error transfer coefficients of second harmonic Tab. 1 amplitude
图6为误差传递系数曲线.结合图6可以看出,等距修形量引起的误差系数为-1.Krp为移距修形产生齿廓误差的传递系数,它的变化为最上面的一条曲线,该曲线包含一个零次谐波系数[8],其值为0.919,说明移距修形量 Δrp中有0.919Δ rp是等效于等距修形量.由于移距修形在齿顶和齿根处的修形量较大,在齿廓中部的修形值较小,且有两个最小值,所以包含一个2次谐波,又由于其幅值不大,占的比重较小,所以系数为 0.045;同时还包含有3次谐波和4次谐波等.偏心距引起的误差系数 Ka比较大,在实际修形时,不采用偏心距修形,且在加工过程中,机床要精确调整偏心距,使其产生的齿形误差最小,使偏心距引起的齿形误差值尽量小,在计算修形量时,也同时计算出偏心距误差,以便调整机床时再进一步减小它.

图6 误差传递系数曲线Fig.6 Error transfer coefficient curves
在频域下,根据表1可构成方程式

式中 A0、A1、A2分别为摆线齿轮一个齿廓范围内的零次、1次、2次谐波分量.
将实验中求得的整个齿廓上测得点的法向误差进行傅里叶变换,求得各次谐波的幅值,将零次谐波、1倍齿频次谐波和 2倍齿频次谐波的幅值带入式(2),得到

解上述联立方程,得到

6 结 语
文中详细介绍了摆线齿轮的极坐标跟踪测量技术.研究表明,采用该测量技术可以对摆线齿轮的齿廓进行高效率、连续自动跟踪测量.通过对等啮合相位角的采样方式进行分析并进行相应的实验,求解出摆线齿轮的修形量.采用傅里叶变换的方法求解修形量可以消除安装偏心和机械传动链中的 1次谐波误差,减小了传动链中其他各次谐波误差的影响,计算出的测量值较符合实际情况.
[1]李 真,庄葆华,吴 迈,等.摆线齿轮误差与测量技术[J]. 机械传动,1997,21(1):38-41.
Li Zhen,Zhuang Baohua,Wu Mai,et al.The cycloidal gear error and measuring technology[J].Journal of Mechanical Transmission,1997,21(1):38-41(in Chinese).
[2]Lin Qijun,Guan Zhongmin. Measuring method of epicycloid rotor profile on 3-D coordinate measuring machine[C]//Proceedings of the1st China-Japan International Composition on Precision Machinery and Instrument Engineerings.Shanghai,China,ISPIE’97,1997.
[3]郑晓峰,方 凯,黄迎华. 一种基于DSP和FPGA的多轴运动控制卡的设计[J]. 自动化与仪器仪表,2006(4):18-20.
Zheng Xiaofeng,Fang Kai,Huang Yinghua.One kind of design for multiple spindle movement control card based on DSP and FPGA[J].Automation and Instrumentation,2006(4):18-20(in Chinese).
[4]李 真,庄葆华,吴 迈,等.摆线齿轮误差测量仪[J].工具技术,1996,30(5):39-42.
Li Zhen,Zhuang Baohua,Wu Mai,et al.The cycloidal gear error measuring instrument[J].Tool Engineering,1996,30(5):39-42(in Chinese).
[5]齿轮手册编委会.齿轮手册(上册)[M]. 2版.北京:机械工业出版社,2001.
Gear Handbook Editorial Committee.Gear Handbook(Volume one)[M]. 2nd ed. Beijing:China Machine Press,2001(in Chinese).
[6]翟海云.摆线齿轮误差及其在线检测技术的研究[D].天津:天津大学精密仪器与光电子工程学院,1998:1-10.
Zhai Haiyun. Study on the Cycloidal Gear Error and Its On-Line Measurement Technology[D]. Tianjin:School of Precision Instrument and Opto-Electronics Engineering,Tianjin University,1998:1-10(in Chinese).
[7]张世安.摆线针轮行星传动中摆线轮最佳修形量的分析与计算[J]. 机械科学与技术,2002,21(6):906-908.
Zhang Shi′an.The optimum profile analysis and calculation on cycloid disks in the cycloid gearing mechanism with small teeth difference[J].Mechanical Science and Technology,2002,21(6):906-908(in Chinese).
[8]翟海云,毕锋杰,陈林才,等.摆线磨齿加工误差的研究[J]. 机械传动,1998,22(2):20-22.
Zhai Haiyun,Bi Fengjie,Chen Lincai,et al.Study on the cycloidal attrition gear’s processing error[J].Journal of Mechanical Transmission,1998,22(2):20-22(in Chinese).
