汽车变速器传动齿轮对角修形量计算方法
2014-11-22褚超美
郭 枫, 褚超美
(上海理工大学 机械工程学院,上海 200093)
近年来,随着最高车速的不断提升,汽车变速器齿轮系统转速及载荷明显增加,已成为汽车变速器振动及噪声的主要影响因素.国内外理论研究及实践表明,齿轮修形是降低齿轮系统振动及噪声的有效措施[1].齿轮的修形方法有多种,传统的齿向及齿形修形方式能够很好地解决圆柱直齿轮的振动及噪声问题,并且修形量的计算方法已基本成熟.然而汽车变速器多以圆柱斜齿轮副来传递动力,由于斜齿轮的啮合线与轴线呈一定角度,传统的齿向及齿形修形方式将改变接触线上的载荷分布,增加了斜齿轮修形的难度.
对角修形主要应用于斜齿轮,修形量随接触线的推移而变化,而同一条接触线上的修形量基本上相同,最大修形量位于啮入或啮出的端部[2].修形区域见图1,Δ 为对角修形量.对角修形可运用径向剃齿或磨齿来实现[3],其修形齿面与渐开线齿面沿接触线相切,且齿对间基本保持全长接触,对重合度影响较小[4].因此,合理确定对角修形量对降低汽车变速器振动及噪声意义重大.
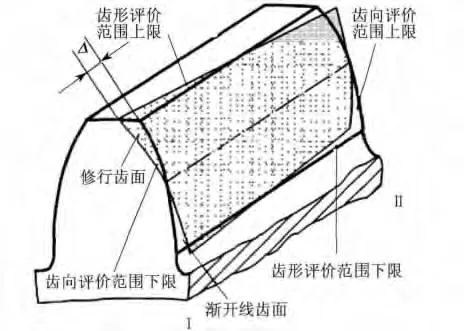
图1 斜齿轮对角修形区域示意图Fig.1 Diagram of bias aera of helical gear
由于对角修形方法的独特性,传统的齿向及齿形修形方法的有关计算公式无法直接应用于对角修形.王宪法等[3]以降低齿轮啮合刚度波动为前提,讨论了窄斜齿轮对角修形区域的选择原则,并提出了对角修形量的计算公式.本文则从齿轮几何学角度出发,首先根据对角修形参数的几何定义,建立斜齿轮副对角修形齿面的啮合方程,并根据啮合齿面连续相切接触条件来确定对角修形量,同时分析对角修形量对斜齿轮副啮合传动误差及啮合斑点的影响规律.
1 建立齿轮副工作齿面啮合方程
1.1 建立理论齿面方程
根据齿轮啮合原理,利用坐标变换的方法,建立斜齿轮副啮合齿对工作齿面的方程.
斜齿轮齿面是由标准渐开线绕基圆轴旋转并同时沿此轴平移的合成运动所形成的曲面[5],建立坐标系SⅠ,p和SⅡ,p分别与主动轮工作齿面的两个理论端面渐开线固定连接,坐标系Sh与变速器壳体固定连接,如图2所示,表示主动轮理论工作齿面的形成过程.
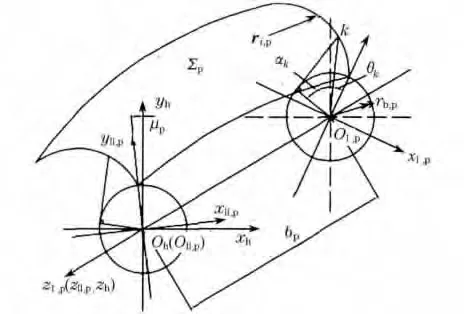
图2 斜齿轮渐开线齿面形成过程示意图Fig.2 Diagram of the formation process of involute flank of helical gear
图2中,曲面Σp是主动轮理论工作齿面,ri,p是理论端面渐开线,rb,p是基圆半径,k 是ri,p上任意一点.则ri,p是角Φk,p的函数
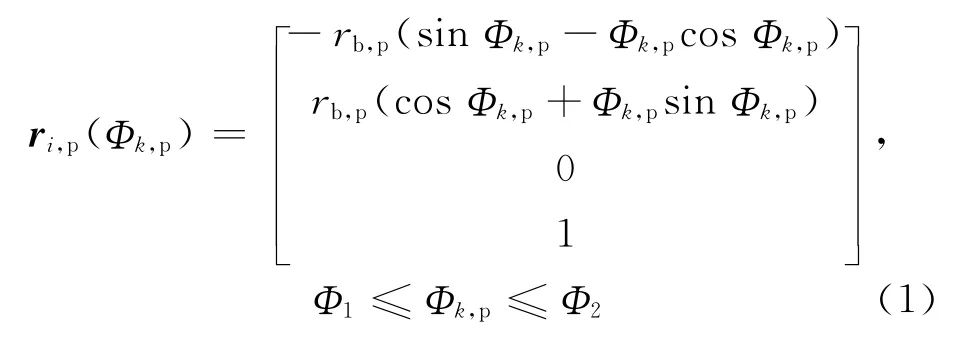
式中,Φk,p是ri,p上k点展角θk与压力角αk之和;当点k分别为ri,p上工作段起点及终点时,角Φk,p分别取Φ1和Φ2.
渐开线ri,p绕轴zⅠ,p逆时针旋转角度Ψi,p,同时沿轴zⅠ,p平移距离bi;并且0≤Ψi,p≤Ψmax,p,0≤bi≤bp,bp为 轮 齿 齿 宽.当 平 移 距 离 等 于bp时,旋转 角 度 达 到 最 大 值,即Ψi,p=Ψmax,p.Ψi,p与bi的关系有

式中,pp为螺旋比,pp=Hp/2π,其中Hp是螺旋线的螺距.
利用坐标变换的方法推导齿面Σp的方程,在坐标系SⅡ,p中表示为rⅡ,p

式中
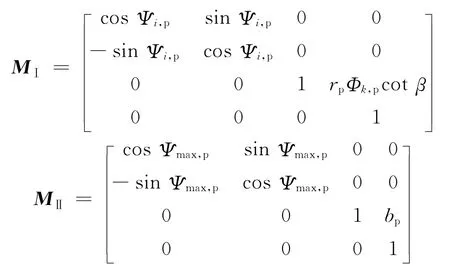
式中,rp为主动轮端面分度圆半径;β 为螺旋角;Φ1≤Φk,p≤Φ2,0≤Ψi,p≤Ψmax,p.
齿面Σp通过坐标变换在坐标系Sh中表示为rh,p
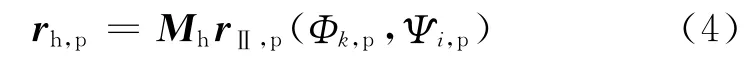
其中,
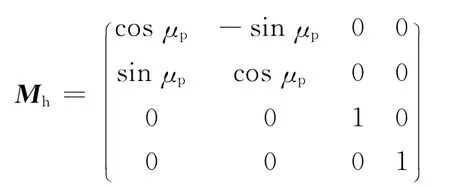
式中,μp 为齿槽半宽角.
与齿面Σp相啮合的被动轮理论工作齿面Σw在坐标系Sh中的表示rh,w
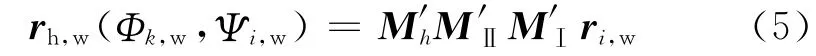
1.2 建立对角修形量方程
根据齿轮标准BS ISO 21771-2007,对角修形是在齿向评价范围的左右极限处渐开线法向压力角的变化.将上述齿形变化简化为渐开线在法向上的线性偏移,即修形曲线采用直线式,则对角修形量也是Φk及Ψi的函数.主动轮对角修形量可表示为
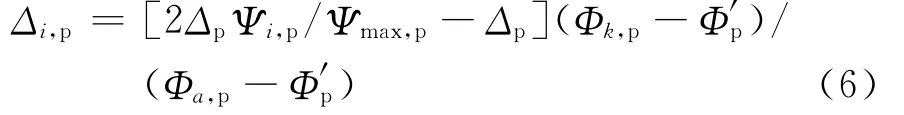
式中,Δi,p为ri,p上k 点法向偏移量;Δp为渐开线偏移量在齿形评价范围上限的值,即主动轮对角修形量;Φ′p为渐开线节点处展角与压力角之和;Φa,p为渐开线齿顶处展角与压力角之和.
被动轮对角修形量可表示为
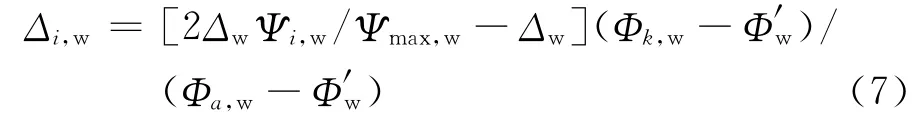
将对角修形量方程代入齿面Σp和Σw中,得对角修形后齿面rh,p,mod和rh,w,mod
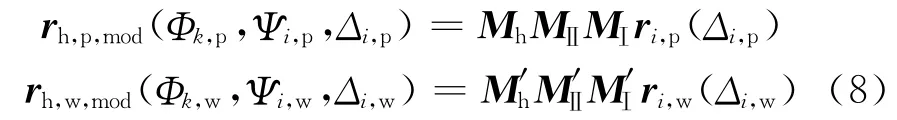
1.3 实际齿面啮合方程的建立
在齿轮啮合过程中,被动轮的实际位置与理论位置之间存在偏差即传动误差(transmission error,TE).国内外研究表明,传动误差是产生噪声及振动的主要激励,减小传动误差可以有效减少振动和噪声[6].
设传动过程中主动轮与被动轮理论旋转角度分别为ωp和ωw,传动比为N,则N=ωw/ωp.因有传动误差的存在,设被动轮实际旋转角度ω′w,则ωTE=ω′w-ωw即为传动误差.在坐标系Sh中,被动轮实际齿面rh,w,mod,act的方程应包括传动误差

式中,
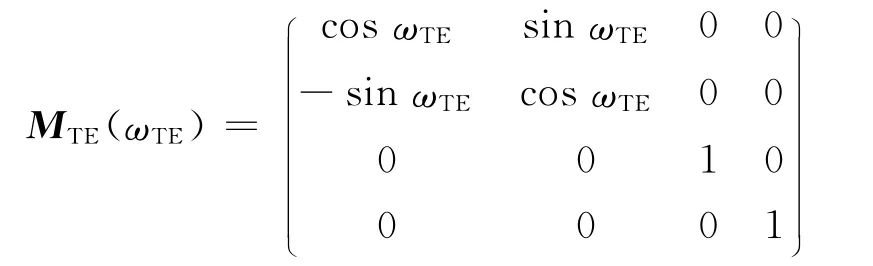
设两齿面Σp和Σw的法向量分别为np和nw,则有

式中,xp,yp,zp,xw,yw,zw分别是主、被动轮实际工作齿面在坐标系Sh中的坐标.
在实际啮合过程中,斜齿轮两啮合工作齿面在固定坐标系Sh中任意瞬时连续相切接触的条件为[7]
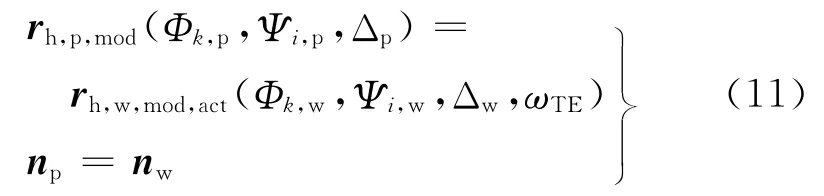
式(11)即为实际齿面啮合方程,其中包括2个矢量方程,共有6个未知数:Φk,p,Ψp,Φk,w,Ψw,Δp和Δw.传动误差ωTE设为常数,取额定工况下被动轮实际位置与理论位置的最大偏差.在给定参数Φk,p,Ψp,Φk,w和Ψw取值范围时,可确定主、被动轮对角修形量Δp和Δw.
1.4 啮合方程的等效解法
将上述啮合方程组(11)的求解问题转化为求两啮合齿面Σp和Σw间距最短及法向量角度偏差最小的优化问题[7],可表示为两齿面向量差的2范数与法向量外积的2范数的和,并求其最小值
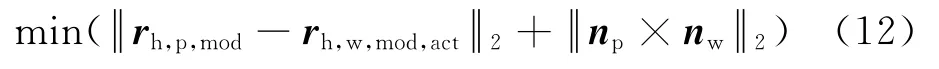
利用Matlab优化工具箱中有约束非线性优化函 数fmincon,求 得 最 优 解Δp(Φk,p,Ψp)和Δw(Φk,w,Ψw),作为实际对角修形量的参考值.
2 确定对角修形量初值
2.1 正交仿真试验应用分析
式(12)中对角修形量的初值需根据经验来确定.根据正交试验的原则进行仿真试验,研究不同对角修形量对传动特性的影响,并选取对角修形量的初值.
在实际啮合过程中,希望齿轮传动在保证强度及寿命的前提下尽量降低噪声及振动.根据经验选择传动误差和啮合斑点作为衡量齿轮传动特性的指标.将主、被动轮对角修形量Bp,Bw作为影响因素,并考虑其交互作用(Bp×Bw)的影响.根据经验,主、被动轮对角修形量各选择4个水平,Ⅰ:3μm;Ⅱ:7μm;Ⅲ:11μm;Ⅳ:15μm.齿轮系统额定工况扭矩64Nm,最大扭矩120Nm.常用工况为:30%~80%扭矩工况,即输入扭矩为36~96Nm.
正交表的选用原则是要考察的因素及交互作用的自由度总和必须不大于所选正交表的总自由度[6].所考察因素及其交互作用自由度总和为:(4-1)×(4-1)+(4-1)+(4-1)=15.正交表L16(45)的总自由度为:(16-1)=15.因此从常用正交表中选用正交表L16(45)[8].
2.2 仿真试验结果分析
综合考虑影响齿轮传动特性的各种因素,并适当地简化,使用英国SMT 公司的Masta仿真软件建立完整的某汽车变速器传动机构仿真模型.目标机型修形齿轮副参数见表1.
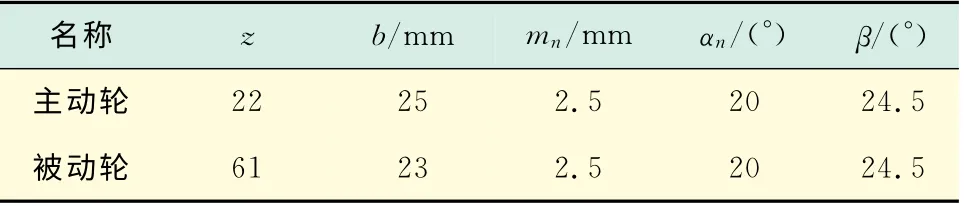
表1 修形齿轮副参数Tab.1 Parameters of modified gear pair
表1中,z为齿数;b为齿宽;mn为法向模数;αn为法向压力角;β为螺旋角.修形齿轮副原设计修形参数为:主、被动轮齿顶修缘量均为10μm;主、被动轮齿形鼓形量均为5μm;主、被动轮齿向鼓形量均为8μm,且采用等半径圆弧设计.
根据正交表L16(45)进行仿真试验,并对试验结果进行比较分析,选取最优水平及各指标的主要影响因素,分析对角修形对传动特性的影响.不同水平对角修形量在不同扭矩下的传动误差比较见图3.
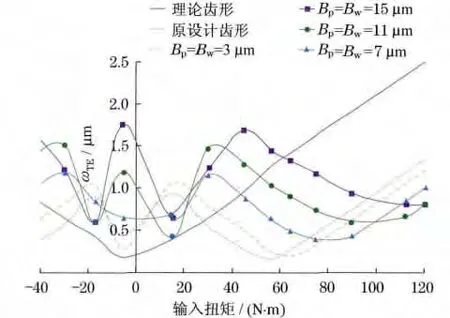
图3 不同水平对角修形量对传动误差的影响Fig.3 Influence of different levels of bias on transmission error
由图3可见,对角修形量均为3μm 时,常用工况下的传动误差较原设计齿形明显降低,但小扭矩及负扭矩工况下传动误差出现波动;随着修形量的增加,扭矩越大,传动误差降低越多,但传动误差降低的工况范围减小.
在额定工况即扭矩为64N·m 下,不同水平对角修形量对啮合斑点的影响如图4所示(见下页).可见,原设计齿形齿面载荷分布与轴线平行;而对角修形后齿面载荷沿接触线方向,分布更加合理;随着修形量的增加,最大接触应力先减小后增大.
根据试验结果作出额定工况下传动误差趋势图,如图5所示(见下页).可见,主、被动轮对角修形量Bp和Bw对传动误差的影响大致相当,其交互作用对传动误差的影响较大.随着修形量的增加,传动误差的值不断增大,即对角修形量不宜过大.最优修形量水平为Ⅰ水平,即Bp=Bw=3μm.
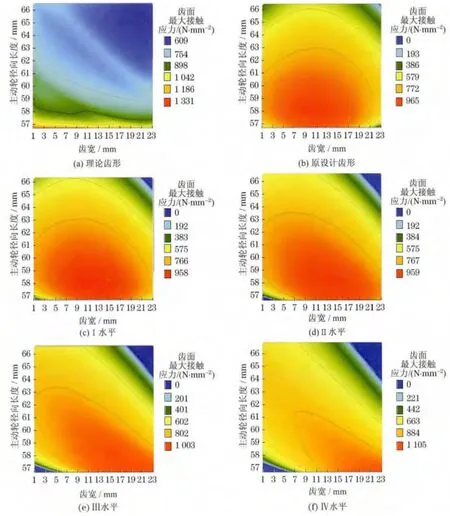
图4 不同水平对角修形量对啮合斑点的影响Fig.4 Influence of different levels of bias on bearing contact
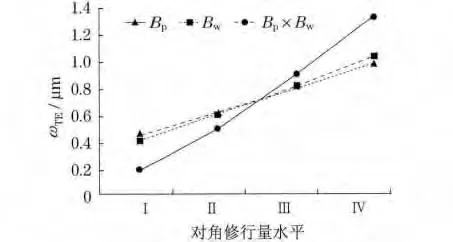
图5 不同水平对角修形量对传动误差影响的趋势Fig.5 Influence trend of different levels of bias on transmission error
3 啮合方程的求解
将试验分析的最优水平作为啮合方程求解的初值,并代入式(12),调用Matlab中fmincon函数求得最优解为Bp=4μm,Bw=5μm,即为额定工况下主、被动轮的对角修形量.用此结果并根据经验再选择几组对角修形量进行仿真试验比较,结果见图6.
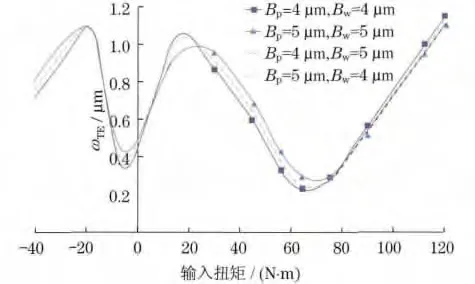
图6 理论计算对角修形量对传动误差的影响Fig.6 Influence of bias theoretically calculated on transmission error
当对角修形量均为5μm 时,大扭矩工况下传动误差降低较多,但此时小扭矩工况下传动误差恶化较严重.当对角修形量均为4μm 时,大扭矩工况下传动误差降低相对较少,但兼顾小扭矩工况,传动误差的改善也相对较好.当主、被动轮对角修形量分别为4μm,5μm 或5μm,4μm 时,修形效果大致相同,且介于上述两者之间.但考虑到经济性及加工工艺性,一般主、被动轮对角修形量相等.因此,综合考虑,目标机型对角修形量确定为Bp=Bw=4μm.在最大扭矩工况下,传动误差为1.15μm,较原设计齿形为1.34μm 下降了14.2%.
4 结 论
a.从齿轮几何学角度出发,建立了斜齿轮副对角修形后两啮合工作齿面满足瞬时相切接触条件的啮合方程.
b.针对齿面啮合方程及对角修形量均是齿形参数角Φk及Ψi函数的特点,提出了对角修形量的计算方法,可应用于不同齿形参数的斜齿轮副. c.根据正交试验仿真分析结果,主、被动轮对角修形量对传动误差的影响大致相当,其交互作用对传动误差的影响较大.随着修形量的增加,传动误差的值不断增大,即对角修形量不宜过大.
d.本研究提出的斜齿轮对角修形量计算方法可在兼顾其它工况的前提下,有效降低常用工况的传动误差,且齿面载荷分布更加合理.
[1]Stephen P.An advanced technology of finishing of topologically modified involute pinion for low-noise/noiseless car transmission[C]∥SAE 2005 Noise and Vibration Conference and Exhibition.Michigan:International Paper,2005:2435.
[2]李贤文,陈谌闻,唐群国.对角修形窄斜齿轮的弹流数值计算和膜厚测试[J].机械传动,1995,19(4):3-6.
[3]王宪法,李华敏.窄斜齿轮对角修形的最佳修形量计算及修形区域的选择[J].哈尔滨工业大学学报,1993,25(5):62-66.
[4]方宗德,张永才.斜齿轮的齿廓修形[J].汽车工程,1993,15(1):59-64.
[5]Faydor L L.Gear geometry and applied theory[M].2nd ed.Chicago:Cambridge University Press,2004.
[6]李润方,王建军.齿轮系统动力学——振动、冲击、噪声[M].北京:科学出版社,1997.
[7]尚振国,王德伦.修形斜齿轮啮和性质及误差影响分析[J].大连理工大学学报,2011,15(1):368-374.
[8]侯化国,王玉民.正交试验法[M].吉林:吉林人民出版社,1986.
[9]方宗德,张永才,蔺天存.斜齿轮的齿廓修形的实验研究[J].机械传动,1992,16(4):27-30.
