基于模糊算法的自调整温度控制系统

赵 阳，曲兴华，李 睿

(天津大学精密测试技术及仪器国家重点实验室，天津 300072)

温度具有非线性、强耦合、时变和大迟滞等特性[1]，在化工、冶金、工业炉窑等生产中，对温度的控制直接影响到许多产品的质量和使用寿命．目前温度的控制大多数采用传统的比例积分微分(proportion integration differentiation，PID)控制，这种控制方法结构简单、工作稳定、鲁棒性较强，但是对于静态与动态性能之间的矛盾、环境温度的变化及空间热源干扰等方面的影响还未能很好地加以解决．而近年来模糊控制技术[2]在这方面提供了新的解决方法，并逐渐被应用于实践中．本文在原有模糊算法的基础上，运用变论域的模糊控制算法．针对非理想的温度控制系统模型，引入了环境温度和控温点两个干扰量，并提出了模糊判决规则的二维查找方法．将此算法用于温度继电器自动检测系统中，使温度的控制可以根据模糊判决规则自动进行，且升降温平缓、快速，最终提高了系统的判断和辨识能力，从而实时地调节温度的变化速度．

1 模糊控制器的设计原理

模糊控制器的作用在于通过电子计算机，根据由精确量转化来的模糊输入信息，按照总结手动控制策略取得的语言控制规则进行模糊推理，给出模糊输出判决，再将其转化为精确量，作为反馈送到被控对象(或过程)的控制作用；反映了人们在对被控过程进行控制中，不断将观察到的过程输出精确量转化为模糊量，经过人脑的思维与逻辑推理取得模糊判决后，再将判决的模糊量转化为精确量，去实现手动控制的整个过程．可见，模糊控制器体现了模糊集合理论、语言变量及模糊推理在不具有数学模型、控制策略只有语言形式性描述的复杂被控过程中的有效作用．

2 变论域的模糊控制原理

在模糊逻辑温度控制中，双输入单输出是最常见的情形．双输入分别是温度偏差和温度偏差变化率，单输出是加热控制输出．在温度多点跟踪的控制过程中，受不同时刻、不同季节的环境温度影响，常规的固定论域以及与之对应的固定模糊判决规则的模糊控制已经不能达到要求，而变论域模糊控制方法则能够准确地调节温度的输出控制量[3]．

变论域模糊控制方法与常规模糊控制系统的差别在于：常规的模糊控制在对输入量进行模糊化及对输出量进行解模糊时，输入和输出量的论域为一定值，而变论域模糊控制是在常规模糊控制的基础上对输入量(温度偏差和温度偏差变化率)和输出量的论域分别加上一个伸缩因子[4]．这样输入量和输出量的论域就随着伸缩因子的变化而变化．

设温度偏差x的论域为[-E，+E]，通过“伸缩”因子α(x)变换为[-α(x)E，α(x)E]，其中α(x)为偏差变量 x的连续函数，α：[-E，E]→[0，1]，x|→α(x)．x的模糊子集分为 7个，即 E＝{ NB(负大)，NM(负中)，NS(负小)，ZO(零)，PS(正小)，PM(正中)，PB(正大)}．设精确变量x的论域对7个模糊状态的隶属度采用三角分布，则论域的膨胀与收缩如图 1所示．

图1 论域的收缩与膨胀Fig.1 Contraction and expansion of the variable domain

任给 x的一个增量Δx，相应地α有一个增量Δα．Δα与Δx呈正比．对于同样大的增量Δx，若 x越大，Δα也应越大；此外，α不超过1，故α越接近1，Δα也应越小，可以得到增量关系式为

式中k为比例常数．把Δx移至左边并令Δx→0，可得

采用分离变量法求解上述方程，则有

式中c为积分常数．根据条件α(0)＝0，可以得到

式中k′为设计参数，须根据实际控制环境来确定．

3 模糊控制输出的自辨别系统

常规的模糊控制中并没有考虑环境温度和控温点的差异．尽管常见的循环控温系统是与外界隔热，理论上不会与外界进行温度交换，事实上并不能完全达到设想状态，环境温度和控温点的影响仍然存在，所以依据控温系统所建立的控制模型中就必须考虑额外两个因素，分别是环境温度和控温点[5]．设环境温度为 T，控制温度为T′，模糊处理中可以改进成如图2所示的结构．

图2 改进的模糊处理系统Fig.2 System of the improved fuzzy processing

以上系统模型的模糊规则的选择要根据环境温度和控温点来查找，在程序中建立一个二维查找表，利用判断语句

可以查找到与T和T′相对应的判决规则．

4 温度继电器检查中改进模糊系统应用

4.1 温度继电器检测原理

生产温度继电器的重要环节是温度特性(升温时的动作温度和降温时的回复温度)的检测[6]．温度继电器通过将两种热膨胀系数相差悬殊的金属或合金彼此牢固地复合在一起形成碟形双金属片，当温度升高到一定值时，双金属片由于下层金属膨胀伸长量大，上层金属膨胀伸长量小而产生向上弯曲的力，弯曲到一定程度时瞬间翻转带动电触点，实现接通或断开负载电路的功能；温度降低到一定值时，双金属片逐渐恢复原状，恢复到一定程度便反向带动电触点，实现断开或接通负载电路的功能，从而把温度变化转换成机械式运动．如图 3所示，当温度上升时，双金属片的中心慢慢地从 O点向 B点移动，当速度变快时，双金属片的中心瞬时间从B点翻转到C点．这时如果温度下降，双金属片的中心从 C点慢慢向 F点移动，当到达 F点时，双金属片中心再次瞬时翻转到G 点(恢复原状)．做成一定形状的双金属片，能按照G →B →C →F →G 反复动作．从 B →C 的温度变化是接通动作温度，从F→G的温度变化是断开动作温度．利用上述反弹特性做成的双金属片式温度开关称为温度继电器．

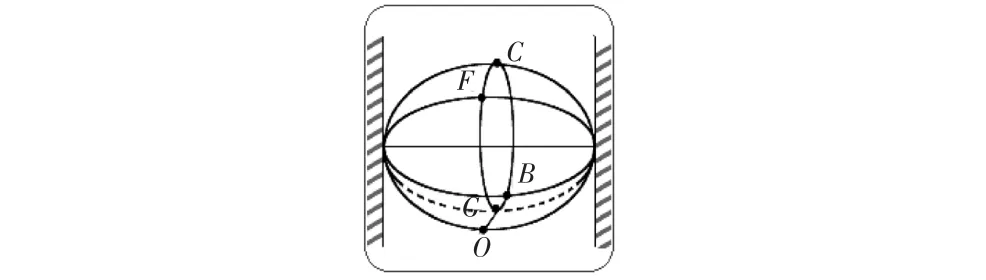
图3 碟形双金属片工作原理Fig.3 Operation principle of the dishing bimetallic strip

经理论分析和反复实验，检测温场的理想控温曲线如图 4所示．θ1为待测温度继电器接通温度的标称值，δ为表征动作温度分散性的参数，即动作温度在这个范围内都是可以被接受的．本例中接通和断开动作温度的上下限为±5,℃．

升温过程中，在0～t1段要快速加热，以提高检测速度，在接近t1点处开始动作温度范围内的温度实时模糊控制，如 t1～t2之间的温度曲线，使温度匀速、平稳上升，给温度继电器以足够的时间做动作．在接近动作温度点的区域内，温度变化速度过快或过慢都不利于实现对温度继电器的高精度检测，变化过快不利于温度的均匀性，过慢又会使检测速率变慢．经过大量实验证明，检测段以1.5～2.0,℃/min升温检测效果最佳．降温过程中，首先要快速降温，当到达断开温度响应范围时，对降温的控制要减慢并加入模糊控制，使温度曲线趋于匀速、平缓地降低，控制的目的也是要给继电器一个较为充裕的动作时间，使动作温度测量值准确．完成一次接通和断开检测后，可再次升温进入下个循环的检测，如图4中t4～t5段所示．

图4 温场自适应控温曲线Fig.4 Adaptive temperature control curve of the Fig.4区性 temperature field

4.2 温度继电器检测系统的系统架构

整个系统是由软件平台和硬件平台两部分组成．硬件平台以工控机为核心，外接串口通讯模块可以实现实验腔温度实时传递和三相固体继电器电力调整器(SSR)的电阻炉丝在线控制．同时通讯模块可以反馈温度继电器状态信号，以供软件及时记录并做出升降温响应，然后控制蜂鸣报警器报警，通知继电器状态变化．系统总体框架如图5所示．

图5 温度继电器检测系统的总体结构Fig.5 Structure of the temperature relay detecting system

电阻加热炉中的温度信号经过热电阻式温度传感器、A/D转换模块输入到工控机，经模糊算法判别处理，得到输出控制量，然后输出值经过 D/A转换模块，输出给三相SSR电力调整器，三相SSR电力调整器输出的电压值加在电阻加热炉丝两端．

鼓风机的作用是加强空气对流，变频器用来调节鼓风机的风速，使实验腔内的气流速度符合检测状态．通过鼓风机的空气对流作用，使实验腔内的温度分布均匀．

制冷压缩机在系统中起到降温冷却的作用，由于控温点的数量较多，并且从低温到高温之间的间隔跨度很大，最高控温点可到 300,℃左右．如此高的温度仅凭自然降温是非常缓慢，也是非常困难的．

在温度继电器检测系统中，还应该通过环境温度传感器测得环境温度，并将其传入系统中，以配合控温点来选择模糊算法判决规则[7]．

4.3 温度曲线拟合及实验数据

4.3.1 温度曲线拟合方法

在本系统中，采取了整体最小二乘法、折线法、折线法与最小二乘法相结合的方法进行误差校准．首先使用高量级的温度测头测定系统检测点处的当前温度，同时读出当前送入计算机的传感器电流模拟量值，在温度范围内测出一组数据；在测量温度数据时，要使温度稳定在一个点上一段时间，在温度值稳定后再读数．由于温度具有较大惯性，很难在一个点稳定一段时间．采用测量时手动调节输出，对输出量进行小范围内调节，使温度在一个点稳定．

温箱采用 SSR热力调整器的阶段性调整供热功率．这样的控制方法造成了温度曲线上升或者下降的非平滑性．不同温度分度内的拟合方程都存有差异．而如果采用折线法制定温度拟合曲线可以较为真实地反映由于分段性控制 SSR热力调整器引起的温度非线性走势，尤其是在结合高阶最小二乘法的分段式温度拟合曲线，可以克服由一阶拟合直线来反映温度变化的不足．

表1所示是标定后的温度传感器测量电流值，以及高精度温度传感器测量的温度值．此处分别利用全局式最小二乘拟合法、折线法和分段式最小二乘拟合法进行温度曲线拟合．

1) 最小二乘法拟合

对表 1数据做最小二乘法 4阶拟合后，得到的拟合多项式方程为

式中I为传感器输入电流值．

最小二乘法拟合后的最大拟合误差 vmax＝0.71℃，平均误差 v＝0.26 ℃，标准差σ＝0.34，极限误差δ＝1.39(99.73%)．从拟合后各点处误差值可以看到，最大的拟合误差出现在第 7点处，即温度为 140℃左右，说明实际曲线并非理想线性．

2) 折线法

本系统使用KST系列单输入通道数字式智能仪表显示温度．该仪表使用折线法补偿输入信号与显示数据的非线性，并在标定时进行修正．从小到大增加输入信号，在此过程中记录下各折线点的传感器电流测量值和温度标准值．

实验中，在温度继电器两极限温度范围内均匀选取段点，分 7段直线拟合，最大拟合误差 vmax＝0.94℃，平均误差v＝0.22 ℃，标准差σ＝0.39．

3) 折线法与最小二乘法拟合相结合

折线法与最小二乘法拟合的关键在于确定段点，而段点的显著特征为段点前后数据拟合曲线斜率的差异明显．对表1数据采用此方法处理，第6、7、8点处偏差最大，存在明显的折点，以此折点将曲线分为4段，每段分别进行最小二乘 4阶拟合，拟合方程各项系数如表2所示．

曲线拟合后的最大误差vmax＝0.22 ℃，平均误差v＝0.06 ℃，标准差σ＝0.10，各项误差指数均小于单独使用最小二乘法和折线法拟合的结果，减小了各点处测量误差，提高了拟合精度和整个区间内测量的可靠性．

表1 标准温度值与传感器电流值Tab.1 Standard temperatures and current values

表2 各段拟合系数Tab.2 Fitting coefficients of each segment

4.3.2 温度继电器通断实验

在 10月份选择相邻(气温条件相似)的两天，对型号为 JUG-7的同一个产品进行连续多次测量，从开机预热完成后每 20,min进行 1次完整的通断测量，分别使用固定论域和可变论域的模糊控制方法进行实验．

1) 固定论域模糊算法实验

考察同一零件通断温度的测量精度和仪器随时间的稳定性．其标准接通温度为 51.0,℃，标准断开温度为50.5,℃．测量结果如表3所示．

表3 固定论域模糊算法通断实验数据Tab.3 Experimental data of the fixed domain fuzzy algorithm

由测量数据可知，接通温度的平均值为 50.9,℃，与标准接通温度的偏差为 0.1,℃，标准差σ＝0.27；断开温度的平均值为 50.7,℃，与标准断开温度的偏差为0.2,℃，标准差σ＝0.31．根据表3绘制图6．

图6呈现3个区间变化趋势：在 09：00—14：00时段内，伴随着室内环境温度的提升，接通和断开温度向上攀升，并且两个特征温度之差也在 0～0.4,℃之间波动；在 14：00—17：00这段时间内，环境温度开始下降，特征温度曲线整体上亦呈现下降趋势；较为平稳的走势集中在 17：00—19：00这个时间段内，不仅两个特征温度走势较为平稳，而且温度间隔也趋近定值．

图6 固定论域模糊算法实验曲线Fig.6 Experiment curves of the fixed domain fuzzy Fig.6院 algorithm

2) 可变论域模糊算法实验

通常情况下，09：00—17：00环境温度变化较为迅速，09：00—14：00 环境温度上升，14：00—17：00环境温度下降，17：00—19：00环境温度较为稳定，呈现缓慢下降趋势．首先，应该在环境温度变化较为快速的时间段内提出相应的变论域系数，然后根据室内环境温度的变化速度和温度高低来自动判定使用哪个变论域系数，当环境温度变化较快时，应该缩小模糊算法的论域范围，提高系统的反应速度[8]．

本实验在 09：00—14：00之间将论域缩短为正常情况的 80%，根据式(5)，温度继电器的通断温度公差为±5,℃，得到论域伸缩因子k′＝0.064．

在 14：00—17：00之间将论域缩短为正常情况的 90%，根据式(5)，取温度继电器的通断温度公差为±5,℃，得到论域伸缩因子k′＝0.092．

在上述两个时间段内做论域收缩的模糊算法处理，得到继电器通断温度实验数据如表4所示．

由测量数据可知，接通温度的平均值为 50.9,℃，与标准接通温度的偏差为 0.1,℃，标准差σ＝0.12；断开温度的平均值为 50.7,℃，与标准断开温度的偏差为0.2,℃，标准差σ＝0.13．由表4绘制了图7．

由上面的两组数据和图表可以直观地看出，变论域模糊算法对于环境温度变化带来的干扰抵抗力更强，特征温度曲线波动更小．环境温度的上升或者下降会带来箱体内温度控制的不稳定性，例如环境温度上升趋势明显，则当箱体内温度也在上升且恰好达到温度继电器的接通温度点、触发继电器的接通动作时，由于此机械动作的延迟以及软件状态捕捉的延时，使得最终系统实测的特征温度值偏高于该产品的接通温度．正是由于环境温度的上升加速了箱体内控制温度变化，使得这个偏差值更加明显．而变论域模糊算法正是针对环境温度这一干扰源，对模糊控制域做相应缩小，对环境温度的变化灵敏度更高，能够更快速地做出温度调整．论域伸缩因子k′在每个时段都有差异，但在同一季节的每天的同一时段相差不会很大．可以根据季节的不同设置对应的每个时段的伸缩因子k′，这样也提高了该系统对外界环境的自适应性．

表4 可变论域模糊算法通断实验数据Tab.4 Experimental data of the variable domain fuzzy algorithm

3)总结

对比以上基于固定论域和可变论域的模糊算法的实验结论，可以很明显地了解到变论域的模糊算法能够使不同时段的温度控制更加平稳、舒缓，从而在一定程度上解决了由于环境温度未达到恒温标准而使待测工件的特征温度随着时间的延续而有较大的差别，即重复性能较差，严重影响了测量的准确度和精度．排除环境温度的变化带来的干扰，可以很大程度上提高模糊控制算法的现场抗干扰能力及系统的稳定性．

图7 可变论域模糊算法实验曲线Fig.7 Experiment curves of the variable domain fuzzy ig.7 algorithm

5 结 语

对温度继电器检测系统的不理想的温度控制模型做了补充，将环境温度和控温点的影响引入到模型分析中，提出了基于变论域算法和根据环境温度对模糊判决规则作相应选择的解决方案，并设计了基于模糊算法的改进控温系统．实验结果表明，该种方法相比以往未经改进的系统更稳定，对温度的控制更准确，重复性更好，抗气候和环境温度的影响也更强．所以，可以看出对模糊算法的改进方案在温度控制系统中是非常有效且适用的．

［1］张立平，曲兴华，孟宪伟，等. 温度继电器温度特性自动检测方法研究及应用[J]. 传感技术学报，2007，20(8)：1907-1911.

Zhang Liping，Qu Xinghua，Meng Xianwei，et al. Research and application of automatic measuring method of temperature relay[J].Chinese Journal of Sensors and Actuators，2007，20(8)：1907-1911(in Chinese).

［2］Sanchez-Lopez A，Arroyo-Figueroa G，Villavicencio-Ramirez A. Advanced control algorithms for steam temperature regulation of thermal power plants[J].International Journal of Electrical Power and Energy Systems，2004，26(10)：779-785.

［3］Montes J C，Llorca R M，Fernández L M. Interpretable fuzzy models from data and adaptive fuzzy control：A new approach[C]//IEEE International Conference on Fuzzy Systems．London，UK，2007：1591-1596.

［4］李洪兴. Fuzzy控制的本质与一类高精度Fuzzy控制器的设计[J]. 控制理论与应用，1997，14(6)：868-872.

Li Hongxing. The essence of fuzzy control and a kind of fine fuzzy controller[J].Control Theory and Applications，1997，14(6)：868-872(in Chinese).

［5］Zheng F J， Shi F， Feng X G，et al. Real-time fuzzy control for a kind of multivariable object[C]//Proceedings of the IEEE International Conference on Industrial Technology．Shanghai，China，1996：617-620.

［6］李 睿，曲兴华，王 义，等. 温度继电器温度特性检测系统的研制[J]. 传感技术学报，2004，17(3)：414-419.

Li Rui，Qu Xinghua，Wang Yi，et al. Develop for measuring system of measuring temperature characteristic of temperature relay[J].Chinese Journal of Sensors and Actuators，2004，17(3)：414-419(in Chinese).

［7］Thompson R，Dexter A. A fuzzy decision-making approach to temperature control in air-conditioning systems[J].Control Engineering Practice，2005，13(6)：689-698.

［8］Precup R E，Preitl S，Kilyeni S，et al. Iterative learning control approach to fuzzy control systems development[C]//The International Conference on Computer as a Tool. Warsaw，Poland，2007：692-697.