大型水电站分层取水叠梁门的脉动压力特性
2011-05-10宋慧芳高学平
宋慧芳,高学平,张 磊
(天津大学建筑工程学院,天津 300072)
近年来,随着对环保的重视,考虑到水体温度在大型水库中具有明显的沿深度成层型分布的特点,从不同库区水深度处放出的水,其水温显著不同,从而影响到下游的生态环境和用水效果.水电站分层取水方式正逐渐被采用,这种进水口结构设置多层叠梁门,以便根据不同水位在不同季节通过调节叠梁门的高度以达到引用水库表层水体的目的.
分层取水叠梁门的过流方式与通常的平板闸门过流方式有明显不同,水流从叠梁门顶流过而不是从闸门底部流过,因此其流激振动也与通常的平板闸门有所区别,目前对平板闸门流激振动的研究多是针对平板闸门闸下泄流引起的振动[1-5],而对叠梁门上过流引起的流激振动研究成果甚少.闸门在水流中的振动是闸门结构与水流相互作用、相互影响的过程,目前对于水流诱发振动分析而言,主要有两种方法[6]:一种是重力-弹性相似的水弹性模型试验,直接在模型上量测水流引起的流激振动特性;另一种是在重力相似的水力学模型量测作用在结构上的脉动水压力,然后建立数值模型计算闸门的流激振动特性.前一种模型试验需要严格做到水动力系统和结构动力系统的完全相似,在配置与水流-钢闸门系统严格水弹性相似的模型材料方面是比较困难的,且模型制作耗资较大;后一种方法只需要在常规的水力学模型上量测作用在闸门上的水流脉动压力,然后将试验所获得的水流整体脉动荷载作为荷载过程作用在闸门结构的有限元模型上进行瞬态时程分析,即可得到闸门的流激振动特性.对于第 2种方法而言,量测并分析作为闸门激励荷载的水流脉动压力是分析闸门流激振动的关键之一.雷艳等[7-8]通过布置在叠梁门上部和下部以及检修闸门的上、下游的4个测点,对分层取水进水口脉动压力进行了模型测量和分析,并对脉动压力最大幅值的取值进行了分析,但没有对作用在叠梁门上的水流脉动压力进行专门研究.
笔者通过水流模型试验量测作用在叠梁门上的水流脉动压力,并结合流场数值模拟结果对水流脉动压力分布规律和荷载特性进行了分析,其结论可为闸门振动分析提供荷载依据.
1 叠梁门水流脉动压力的量测与结果
1.1 模型设计和量测仪器
模型以某水电站工程设计为依据,进水口采用有机玻璃制作,模拟中间的3个进水口,包括拦污栅槽、叠梁闸门、检修闸门、事故闸门及通气孔、渐变段、部分引水管段等,图 1为进水口示意.各试验工况的主要参数见表1.

图1 进水口和模型试验布置示意Fig.1 Schematic of inlet and layout of model test

表1 模型试验工况参数Tab.1 Parameters in model test
测点的布置和测试框图如图2所示,其中各测点都位于闸门结构上横水流方向的中心点处.模型各机组的过流量由调节阀控制,在下游的量水堰测量.试验中采用点压力传感器测量了不同工况下 5#进水口叠梁门上的点脉动压力荷载,压力传感器在安装时保证与叠梁门面板垂直,避免存在影响测量准确性的倾斜和凹凸不平现象.水流荷载作用在压力传感器上,通过数据线传入数据采集系统,由计算机进行分析并输出结果.该水电站根据实际情况拟设置 3层叠梁门取水方案,工况 1为 1层叠梁门取水方案,放下1节闸门,单节闸门高12.68,m(压力测点为1#~8#);工况2为2层叠梁门取水方案,放下2节闸门,2节闸门高 25.36,m(压力测点为 1#~16#);工况 3为 3层叠梁门取水方案,3节闸门全部放下,3节闸门高38.04,m(压力测点为 1#~24#),其中奇数号(1#,3#,5#,…,23#)测点用于量测闸门上游侧所受到的脉动压力,偶数号(2#,4#,6#,…,24#)测点用于量测闸门下游侧所受到的脉动压力.

图2 压力测点布置示意Fig.2 Arrangement of pressure measuring points
1.2 试验测量结果
在分层进水口水力学模型试验中,经数据采集系统获得的是作用在叠梁门面板上的水流脉动压力的时域波形图,即压力脉动瞬时值的波形,其波形图是极不规则的,且是随机变化的[9],如何对水流脉动压力波形图加以分析,关系到能否为该结构设计方案提供正确荷载依据.现有的对于脉动压力的分析方法主要有两种:数理统计分析方法和频谱分析法.
通过对试验中采集到的不同工作水位下不同叠梁门运行工况时叠梁门上各点对应的脉动压力结果进行功率谱分析的方法,对作用在叠梁门上的水流脉动压力进行了分析.功率谱分析是把傅里叶分析法和统计分析方法两者结合起来考虑的.
水流脉动荷载为各态遍历的平稳随机变量,水流中一点脉动压力p′的相关函数为

可以通过傅里叶变换得到频率空间相应点的脉动压力频谱 Sp′p′(ω),即
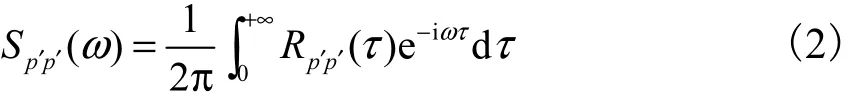
其逆变换为

在进行功率谱的实际计算时,并不是采用直接由脉动压力的相关函数来求其功率谱密度函数,而是通过快速傅里叶变换(fast Fourier transform,FFT)技术,直接求得各测点的水流脉动压力的功率谱函数及各测点之间的互谱密度函数.
表2~表4分别给出了3种工况下各测点脉动压力功率谱分析结果,图3和图4分别给出了工况1的1层叠梁门工作时和工况2的2层叠梁门工作时闸门上部分测点的脉动压力时域波形图和功率谱分析结果.

表2 脉动压力功率谱分析结果(工况1)Tab.2 Power spectrum analytical results of fluctuating pressure(case 1)

表3 脉动压力功率谱分析结果(工况2)Tab.3 Power spectrum analytical results of fluctuating pressure(case2)

图3 工况1部分测点脉动压力时域波形及功率谱曲线Fig.3 Time domain waveforms and power spectra of fluctuating pressure in case 1
从试验结果可以看出:①在各工况下叠梁门的不同部位脉动压力特性有所不同,在叠梁门下游侧底部位置出现了较大的脉动压力,而作用在叠梁门上游侧和下游侧上部的水流动水压力接近于静水压力,没有明显的压力脉动现象;②作用在叠梁门下游侧底部处的脉动压力优势频率均在 0.1,Hz左右,属于低频动荷载;③随着叠梁门高度的增加,闸门底部脉动压力的范围也增大.

图4 工况2部分测点脉动压力时域波形及功率谱曲线Fig.4 Time domain waveforms and power spectra of fluctuating pressure in case 2
2 试验结果分析
由于叠梁门附近的水流流态直接影响其荷载特性,为进一步分析作用在叠梁门上脉动压力形成的原因,本文采用数值模拟手段对进水口的水力特性进行了模拟,数值模拟采用标准k-ε紊流模型.
数值模拟的边界条件如下:库内距进水口较远断面为进流边界,压力按静水压力分布规律给出;引水主管渐变段下游管道断面为出流边界,出流边界流速按引水主管平均流速给出;固壁边界采用无滑移条件,粗糙影响程度由壁函数确定.
模型求解采用有限体积法,二阶迎风格式,压力-速度耦合采用压力校正法,离散方程采用 TDMA法求解,时间差分采用全隐格式.
图5给出了工况3(3层叠梁门取水)时叠梁门附近的流场分布.
综合水力模型试验和数值模拟结果可以有下述结论.
(1) 经叠梁门的下泄水流运动类似于完全淹没情况下薄壁堰的水流运动.不同的是,由于水流受到进水口塔体结构在水流向的约束,形成向叠梁门下游面挤压的有压下曳运动.
(2) 沿叠梁门后下曳的水流,由于门顶的挑射作用,主流偏向进水口结构的一侧,并在叠梁门下游面形成分离的漩涡区.由于塔体的挤压作用,这一漩涡区的厚度(沿进水口方向的尺度)较之薄壁堰后分离区的厚度大为减小,这部分水流对叠梁门顶产生的压力扰动也很小.但是在进水口部位,塔体结构的约束消失,加之受到水流 90°转向的牵引作用,漩涡运动得到充分发展,从而可以将叠梁门后水流形成的漩涡以进水口上缘的高度为界分为上下两部分.在分离区的上部,分离区的水流开始几乎是紧贴着叠梁门的下游面向上回流至门顶附近,再在挑射水流的拖曳作用下向下运移(见图 6).这部分水流对叠梁门的紊动荷载很小,动水压力接近于静水压力.在分离区的下部分,即在叠梁门正对着进水口的部分,充分发展的漩涡形成在垂向尺度与进水口高度同量级、横向尺度与叠梁门净宽同量级的最大涡旋到次生的各级漩涡组成的紊动级联结构,对叠梁门下游的下部分产生强烈的、瞬变的动水冲击作用.按照紊流的发生和发展的理论,最大尺度的涡旋持有最大的紊动能量和较低的脉动频率.图 4中的 2#测点就是在此区域内利用压力传感器测到的典型的瞬时脉动压力的时域波形和功率谱曲线.显然,作用在这一区域的水流脉动压力,无论叠梁门升至任何高程,都是可能诱发叠梁门产生流激振动的主要激振力.
(3) 紊动涡旋的垂向最大尺度与叠梁门的高度有密切关系,工况3水位最高,叠梁门高度也最高,下曳水流具有的惯性也最大,形成的分离区和漩涡垂向尺度就最大,所以工况3叠梁门下游侧较大区域存在较大的脉动压力,且各点的功率谱曲线具有较一致的主频和较相似的曲线形状(见表 2~表 4和图 6),可以认为这4个测点(2#、4#、6#、8#)是在同一个大漩涡的作用下,随着测点高程的增加,高频小漩涡是逐渐减小的,在最底部 2#测点处小漩涡最多,8#测点处的小漩涡最少.
(4) 作用在叠梁门上部分的动水压力,由于水流在叠梁门附近基本与闸门平行,不存在垂直于板面的大的脉动压力,动水压力接近于静水压力.
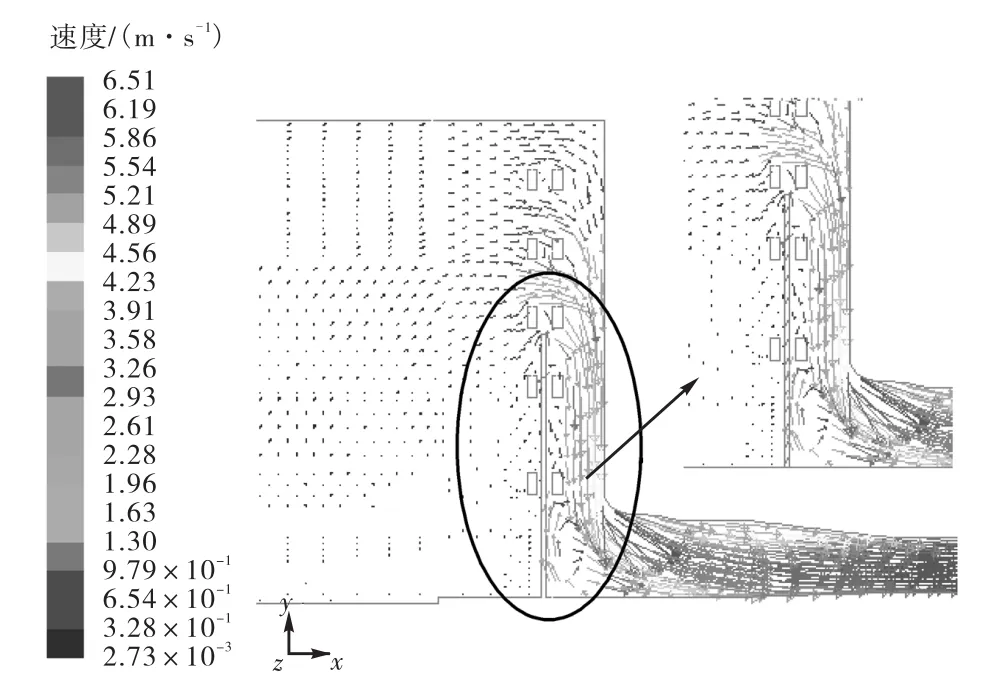
图5 工况3叠梁门附近的流场Fig.5 Flow field near stoplogs gate in case 3

图6 工况3部分测点脉动压力功率谱曲线Fig.6 Power spectra of fluctuating pressure in case 3
3 激振力的点面转换
计算结构物的流激振动需要知道水流整体的脉动荷载,即面上的总脉动荷载.一般情况下,作用在面上各个点的脉动压力是由在相应点附近水流不同尺度漩涡的运动而引起的[10],因此,面上各点的脉动压力通常具有不同的幅值和频率(见图 7(a)).由于均化作用,面脉动压力的幅值P′( t)通常小于点脉动压力绝对值的总和∑ |p ′( x, t)|,而面脉动压力的频率特性是各个不同频率脉动压力频率的综合反映,也与各点脉动压力的频率不尽相同.一般情况下,需要应用按结构可能振动的作用面积特制的面压力传感器直接量测面脉动压力的幅值和频率特性,这就使得水流激振力的量测受到较大的限制.

图7 点脉动压力和面脉动压力示意Fig.7 Point fluctuating pressures and area fluctuating pressures
据上述对叠梁门顶过流水流特性的分析,叠梁门激振力主要来自闸门后侧底部水流转向发生的大漩涡运动,在叠梁门宽度相对于泄水孔宽较窄的情况下,在闸门后侧发生的大漩涡具有准二维漩涡的特性,此时闸门的有效受力面整个地被准二维的大漩涡所覆盖.通常水流紊动的大尺度漩涡的能量直接来自均流,含有紊动能的绝大部分,也是形成紊流能谱峰值-主频率的主要漩涡.在此水流条件下,从对工程产生流激振动的最不利情况考虑,可以将作用在叠梁门上的激振力的点面转换关系做如下的简化.
设在闸门受水流脉动压力有效作用面 Ae上的点脉动压力为p′(x,t)、面脉动压力为p′(t),一般情况下,前者是时域和空域中的随机函数,后者是时域的随机函数,如图 7(a)所示.针对对叠梁门水流特性的分析,略去水流次级漩涡的影响,在某一瞬时 t,在有效面上各点出现幅值相近、位相相同的点脉动压力为p′(t),见图7(b),于是在该瞬时有
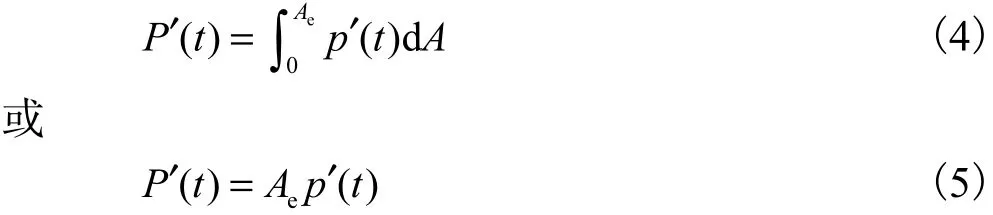
根据概率理论,作为平稳随机函数的水流脉动的面压力和点压力的方差可分别写为

将式(4)代入式(6)并考虑式(7),有
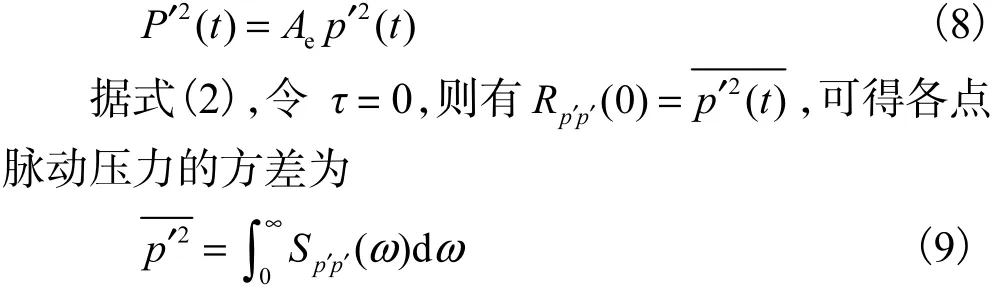
即一点的脉动压力的方差,等于相应频谱曲线下所包含的面积.同理,对于面脉动压力p′(t),有

据式(12)可以将量测的点脉动压力谱转换为引起流激振动所需的水流整体作用在闸门上的激振力.图8给出了根据上述方法计算得到的工况1下作用于叠梁门上下游两侧面脉动压力(激振力)结果,从图中可以看出面脉动压力与点脉动压力的特点相同,作用于上游侧的面脉动压力分布比较均匀,作用于下游侧靠近底部位置的面脉动压力较大.

图8 工况1叠梁门上的激振力Fig.8 Excited power on stoplogs gate in case 1
在计算结构物反应谱(应力谱、位移谱等)过程中,激振力主频率的作用要比其方差间的少许差异重要得多.但上述推导过程中,略去次级漩涡在闸门不同位置处产生的点脉动压力方差值的差异所产生的影响,可以通过选用测点中具有最大脉动压力方差的功率谱来推求最不利的功力反应或其他适中方差的功率谱的功力反应予以补偿.
4 结 论
(1) 各工况下作用在叠梁门不同部位的脉动压力特性有所不同,在叠梁门下游侧底部位置出现了较大的脉动压力,而作用在叠梁门上游侧和下游侧上部的动水压力接近于静水压力.
(2) 在叠梁门下游侧底部位置形成的紊动涡旋的垂向最大尺度与叠梁门的高度有关,水位越高,叠梁门高度越高,由于下曳水流具有的惯性也越大,形成的分离区和漩涡垂向尺度越大.
(3) 作用在叠梁闸门下游底部的水流脉动压力主要是由于水流 90°转向引起的准二维大漩涡产生的,大漩涡含有最强的紊动能量和较低的脉动频率,是可能诱发叠梁门产生流激振动的主要激振力.
(4) 针对叠梁门的水流特性,提出了一种利用量测的点脉动压力转换为计算流激振动所需要的面脉动压力的简化方法.
[1]杨 敏,练继建,林继镛. 水流诱发平板闸门振动的激励机理[J].水动力学研究与进展,1997,12(4):437-449.
Yang Min,Lian Jijian,Lin Jiyong. The excited mechanism of flow-induced vibrations of plate gate[J].Journal of Hydrodynamics,1997,12(4):437-449(in Chinese).
[2]李火坤. 深孔平板工作闸门流激振动物模-数模预测[J].南昌大学学报:工学版,2007,29(4):395-400.
Li Huokun. Prediction of flow-induced vibration of deep plate gate using physical and numerical model[J].Journal of Nanchang University:Engineering and Technology,2007,29(4):395-400(in Chinese).
[3]Thang N D,Lin Q H,Naudascher E. Flexural streamwise vibration of gate plates under vortex action[J].International Conference on Flow Induced Vibrations,1987,37(2):171-181.
[4]Jongeling T H G. Flow-induced self-excited in-flow vibrations gate plates[J].Journal of Fluids and Structures,1988(2):541-566.
[5]Hardwick D J. Flow-induced vibration of vertical-lift gate[J].Journal of the Hydraulics Division,1974,100(5):631-644.
[6]倪汉根,刘永林,刘 斌,等. 弧形闸门流激振动的物模-数模预报[J].水动力学研究与进展(A 辑),2005,20(1):24-32.
Ni Hangen, Liu Yonglin,Liu Bin,et al. Prediction of tainter gate vibration using combined physical and numerical models[J].Journal of Hydrodynamics(Ser A),2005,20(1):24-32(in Chinese).
[7]雷 艳,刘礼华,魏晓斌,等. 某水电站分层取水进水口脉动压力模型试验[J].武汉大学学报:工学版,2007,40(2):70-73.
Lei Yan,Liu Lihua,Wei Xiaobin,et al. Model experiment study on fluctuating pressures in variable elevation intake for a certain hydroelectric station Engineering[J].Journal of Wuhan University:Engineering and Technology,2007,40(2):70-73(in Chinese).
[8]雷 艳,刘礼华,魏晓斌,等. 分层进水口导水叠梁门模型脉动压力最大幅值取值分析[J].水动力学研究与进展(A 辑),2007,22(3):273-277.
Lei Yan,Liu Lihua,Wei Xiaobin,et al. Analysis on determining maximum amplitude of model fluctuation pressure on training stoplogs gate with varying elevation intake[J].Journal of Hydrodynamics(SerA),2007,22(3):273-277(in Chinese).
[9]Ishi I. Flow-induced vibration of long-span gate(Part I):Model development[J].Journal of Fluids and Structures,1992,6(5):539-562.
[10]Zhao Yaonan.Mechanism of wall pressure fluctuation beneath the open channel flow[J].Journal of Hydrodynamics,1989,1(1):55-65.
