波浪条件下海底管线与沙质海床间的相互作用
2011-05-10白玉川杨细根冀自青戚晓明
白玉川,杨细根,冀自青,戚晓明
(天津大学建筑工程学院,天津 300072)
在海洋石油开采过程中,如果由于管道失稳等因素而引起管道内油气的泄露,将造成巨大的经济损失和严重的海洋环境污染,因此需要从管道稳定性出发,研究管道的横向运动和垂直运动.波浪引起的水动力载荷是作用在海底管道上的最主要的动力荷载,而海床土壤提供给管道的侧向阻力是管道得以稳定的主要因素.海底管道的稳定是一个波浪、管道和海床三者之间动力耦合作用的复杂问题.研究管土相互作用,正确评价土体对管道阻力的作用,对于确保管道的稳定性、安全性和经济性,对于完善有关设计规范都有着重要的意义.
数值模拟方面,Verley等[1]对管土相互作用问题进行了量纲分析,提出了描述管道侧向失稳的力-位移模型.针对埋置管线,Lai等[2]在可渗刚性海床的假定下,利用有限差分法和有限单元法对海底埋设管线所受的波浪力进行了数值计算.基于同样的假定,Lennon[3]利用数值方法对该问题进行了研究.Mac-Pherson[4]对海底埋设管线在无限深海床情况下求得了解析解.邱大洪等[5]基于一阶椭圆余弦波理论给出了无限深海床中埋设管线上的非线性波浪渗流力的解析解.任艳荣等[6-7]讨论了ABAQUS软件处理管土作用中的接触面及砂质海床上的海底管道稳定性的问题,宋岩新等[8]将 ABAQUS后处理二次开发应用于海底管线稳定性分析.大量的实验资料和理论知识表明,利用大型商业软件建立数学模型模拟海底管线的受力变形及失稳,具有广泛适用性.笔者选择沙土作为研究对象,研究了波浪条件下海底管线与多孔介质(沙质)海床的相互作用.
1 埋设管线上的波浪力理论计算
坐标选取及部分参数如图1所示.

图1 坐标系的定义Fig.1 Definition of coordinate system


由于渗流遇到管线时发生散射,因此可以把此渗流场内的孔隙水压p分为无管时波浪引起的渗流压力1p和管线引起的摄动压力2p两部分[5],即式中:i为虚数单位;λ为波数;ω为角频率;γf为水的比重;n为孔隙率;ks为渗透系数;βf为孔隙水的压缩系数;G为土的剪切模量;ν为泊松比;r、rl分别为到管线圆心、到第 l个圆圆心的距离;An、Bn可由边界条件的代数方程解得;ly为第l个管圆心的纵坐标.
将波浪渗流压力在管线表面上积分,可得作用于单位长度管线上的总波浪渗流力,分别用 Fh和 Fv表示这个力的水平分量和竖直分量,则
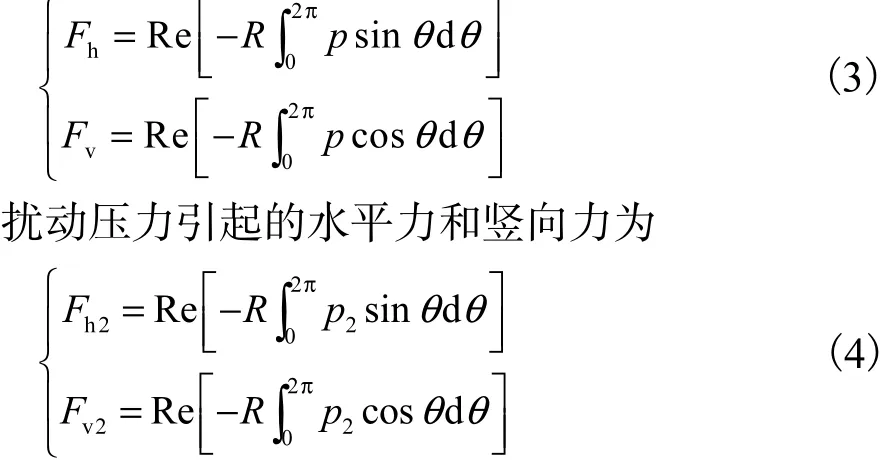
2 ABAQUS中对管土模型的研究
为使模型简单化,采用在岩土工程中常用的Mohr-Coulomb塑性模型,计算中使用Mohr-Coulomb破坏和强度准则.
2.1 管土接触问题
接触问题的特点是具有单边约束和未知接触区域.为此必须解决以下4方面问题:①物理模型;②几何运动规律;③本构规律;④建立方程与求解方法.
ABAQUS中接触算法如图2所示.

图2 接触分析逻辑流程Fig.2 Logical flow chart of contact analysis
2.2 平衡初始地应力
在有关土的工程数值计算中,初始地应力场是必须予以重视的问题.不管采取何种方式施加初始应力场,始终要满足平衡条件和屈服条件,基于这两个条件,假设自重的应力场与静水压力就是初始应力场,直接将重力荷载和静水压力施加于有限元模型中并施加相应的边界约束,计算得到重力荷载下的应力场.再将得到的应力场和重力荷载一起施加于原始模型,便可得到一个既满足平衡条件又不违背屈服准则的没有位移的应力场.
2.3 验证模型
建立长25,m、宽10,m、高10,m 的三维海床土体模型,模拟简单平衡地应力情况,结果如图3所示.

图3 平衡地应力前后土体的位移分布Fig.3 Soil displacement distribution under the unbalanced Fig.3 and balanced in-situ stress
海床模型网格采用 8节点六面体线性减缩积分单元(C3D8R8),管道壳结构网格采用 4节点四边形有限薄膜应变线性减缩积分壳单元(S4R).在海床模型的侧面位移为 S1、S3,施加约束 S1= S3= 0 ,不约束S2(竖直方向 y的位移),在海床底面施加约束S1= S2= S3= 0 .
从图 3可以看出在平衡地应力前土体的位移达到分米的数量级,在平衡地应力后土体位移在微米的数量级,可满足工程要求.
3 管道-海床模型的建立及计算结果分析
3.1 模型的建立及荷载的施加
管土模型由管和海床两部分组成,海床采用连续的三维实体模型;管采用三维壳结构.海床模型长25,m、宽 10,m、高 10,m;管模型直径为 1,m,厚度为0.2,m,埋置在海床下 1.5,m 深(距管道中心).在网格划分时管土接触处进行局部细化.
管土模型受到的主要荷载有管道的自重和波浪产生的动荷载.本文将第2.1节所述的渗流力简化成一对正弦变换的面荷载施加在海床模型两侧,以模拟波浪对海床和管道的作用,并忽略模型上表面的剪切力.在模拟管土作用时,将管道两端固定,海床底部施加三向固定约束,其余边界无约束.
3.2 平衡地应力后的土体位移
对土体平衡地应力后在模型中附加管道,进行数值计算得到土体的竖向有效应力分布,如图 4所示.

图4 平衡地应力后土体竖向有效应力分布Fig.4 Distribution of vertical effective soil stress under bal-Fig.4 anced in-situ stress
3.3 管道在自重荷载下的变化
在上述模型的基础上,增加一分析步,并在此分析步中施加管道在y方向上的荷载.边界约束初始条件保持不变,得到的土体应力变化如图5所示.
在管道自重的作用下管道会发生 y方向的竖直位移,弯曲的位移量级在毫米级,对管道的稳定性影响较大.管道在y方向的竖直位移见图6.
管道在自重荷载的作用下还会产生小变形的屈曲,为验证管道是否发生屈曲,现将管道从中截开,选取沿管道圆周的各点测量其位移(见图 7),发现各点位移均在 1.23×10-3m 的量级,但仍有较小的位移差,这个位移差就是由于管道自身的屈曲而产生的,由于位移差的数量级在 1 0-5m 左右,相对于直径为1,m、壁厚为0.2,m的管道来说,管道自重造成的屈曲对管道的稳定性影响不大.但管道屈曲是破坏海底管道稳定性的最直接的重要原因之一.

图5 施加管道重力后的土体应力Fig.5 Soil stress under gravity

图6 管道在自重荷载下的竖直位移Fig.6 Pipe vertical displacement under gravity
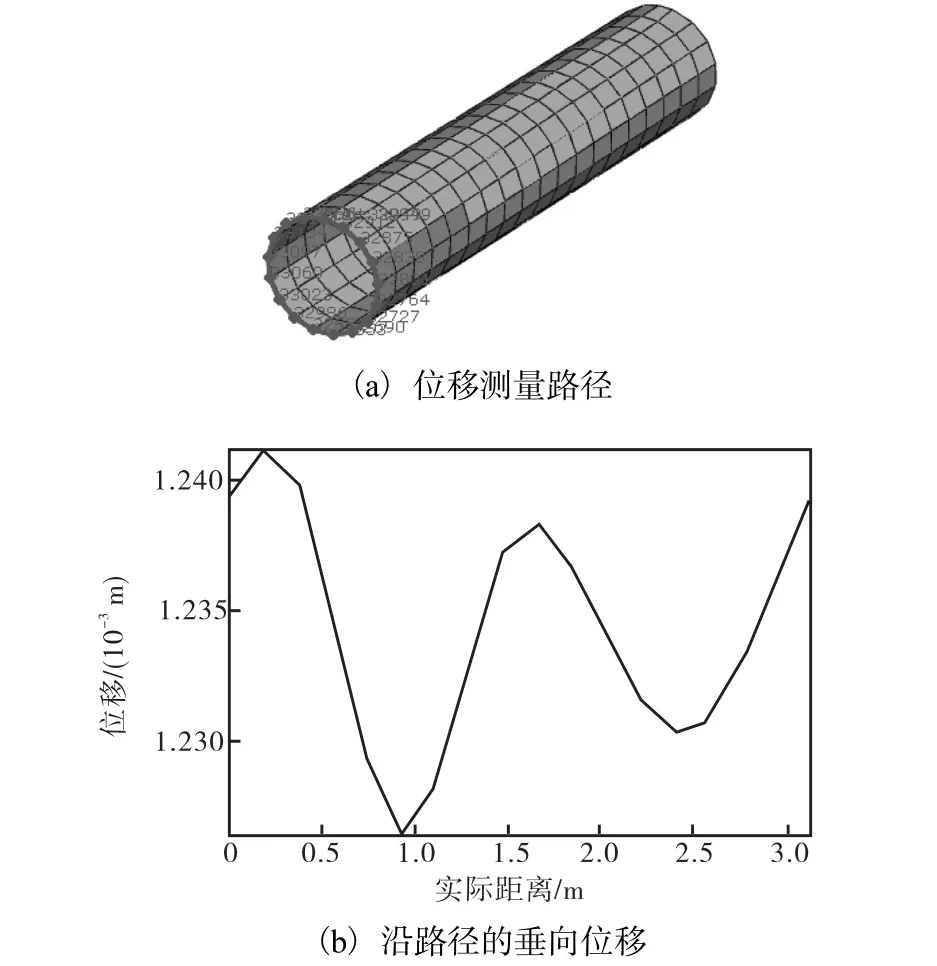
图7 位移测量路径及沿路径的垂向位移分布Fig.7 Schematic of measurement path and displacement Fig.7 map around circle of pipe
3.4 管道在自重和波浪荷载联合作用下的变形
本文模型只是对海床-管道-波浪的初步模拟,故波浪荷载的施加采取简化渗流力的方式,即在海床模型两侧施加一对同向的正弦变化的面荷载.
通过计算得土体的位移如图8所示.

图8 计算得到的土体位移Fig.8 Soil displacement
管道受土体的挤压及自重作用会产生侧向的弯曲,最大位移约为 1 .6× 1 0-4m(见图 9),其值比自重作用下的管道最大变形小1个数量级.
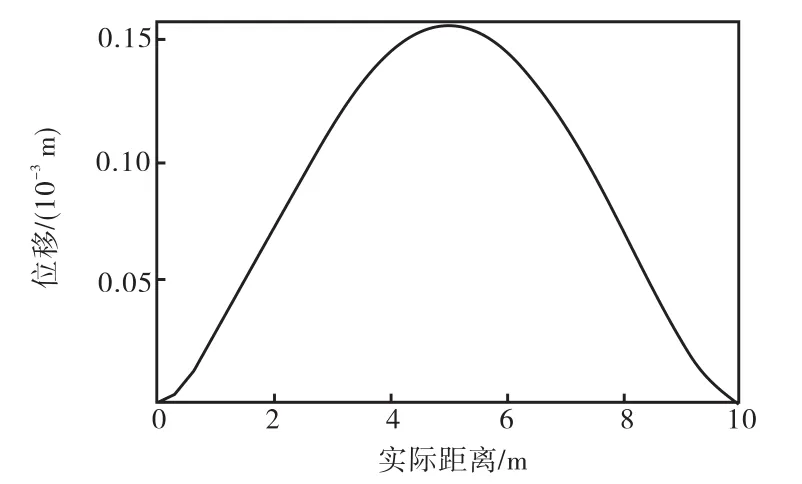
图9 管道沿长度方向在y方向的位移Fig.9 Displacement in y direction at the length
管土模型在两种荷载的作用下,管道既产生水平向(x方向)又产生竖直向(y方向)的位移.在两者的共同作用下,管道将产生较大的弯曲和较小的侧向扭曲.为表现出管道的侧向扭曲,在沿管道长度方向上选取一圆周路径并测出此路径上管道水平向(x方向)的位移,结果见图10.

图10 管道沿管周路径在x方向的位移Fig.10 Displacement in x direction around circle
将图 10中的位移数值与图 9管道总位移相比,可得管道的侧向扭曲位移约为 5 .5× 1 0-7m,远较竖直弯曲位移小.
管道与土体直接的接触作用是影响管道稳定性的重要因素,管道与土体接触面之间产生的压力如图11所示.

图11 管道与土体之间接触压力的变化Fig.11 Varied conact pressure between pipe and soil
3.5 埋置管道的破坏方式
从数值模拟的初步计算结果可以初步得出埋置管道的几种破坏方式:①管道自重及管道中流体重力导致管道产生弯曲,当弯曲挠度大于抗弯挠度时管道就会发生破坏,但实际表明这种破坏一般不会发生;②波浪荷载以及海底的复杂环境造成管道的侧向扭曲,这种变形对管道的破坏较弯曲的危险系数较大;③管道内外温度差以及其他原因造成管道在横断面上的屈曲变形破坏性较严重,如海底热油管道.实际中管道的破坏方式远远不止以上3种,海底环境的复杂性可能造成海底管道更为复杂的破坏方式.
4 结 论
(1) 在利用 ABAQUS软件解决有关土的问题时,若要考虑变形,则必须进行地应力平衡.从验证模型中可以看出平衡地应力的效果明显.平衡初始地应力不仅能够得到重力作用下满足平衡条件、不违背屈服准则的应力场和位移场,较好地体现土的分层现象及结构由于重力荷载在土体产生的附加应力和位移,而且能够较好地体现土对结构的挤压效应,为以后的分析建立良好的接触条件.
(2) 利用 ABAQUS软件对海床进行平衡地应力、周期振荡等处理,建立海管埋设模型,进行受力分析并通过软件进行计算处理后得出管道弯曲变形、屈曲变形曲线,可由此判定管道的破坏形式.
(3) 本文利用 ABAQUS软件对海床-管道模型进行了初步的建模,并简单地施加了重力以及波浪荷载,模拟出的土体位移和管道变形以及管土接触面之间的接触压力等均和实际情况基本吻合.但初步建模的结果误差比较大,造成误差的原因可能有地应力平衡不充分、荷载条件施加较简单等,这种误差在进一步的建模中可以逐步减少.
[1]Verley R L P,Torbjion Sotberg. A soil resistance model for pipelines placed on sandy soils[J].Journal of Offshore Mechanics and Arctic Engineering,1994,116(3):145-153.
[2]Lai N W,Domingguez R F. Numerical Solution for Determining Wave-Induced Pressure Distributions Around Buried Pipelines[R]. USA:Tex A & M Univ Dep Civ Eng Rep COE 182,1974.
[3]Lennon G P. Wave-induced forces on buried pipelines[C]//ASCE.USA,1983:505-518.
[4]MacPherson H. Wave forces on pipeline buried in permeable seabed[J].Journal of the Waterway Port Coastal Ocean Division,ASCE,1978,104(4):407-419.
[5]邱大洪,宋昭晨. 波浪渗流力学[M]. 北京:国防工业出版社,2006.Qiu Dahong,Song Zhaochen.Wave Seepage Mechanics[M]. Beijing:National Defence Industry Press,2006(in Chinese).
[6]任艳荣,刘玉标,顾小芸. 用 ABAQUS软件处理管土相互作用中的接触面问题[J]. 力学与实践,2004,26(6):43-45.
Ren Yanrong,Liu Yubiao,Gu Xiaoyun. Analysis for the interface of the pipe/soil interaction by ABAQUS software[J].Mechanics and Engineering,2004,26(6):43-45(in Chinese).
[7]任艳荣,刘玉标,顾小芸. 利用 ABAQUS软件分析砂质海底管道稳定性[J]. 中国海洋平台,2001(5):68-72.
Ren Yanrong,Liu Yubiao,Gu Xiaoyun. The stability analysis of naked pipeline laying on a sandy seabed based on ABAQUS program[J].China Offshore Platform,2001(5):68-72(in Chinese).
[8]宋岩新,杨 庆,唐小微,等. ABAQUS后处理二次开发在海底管线稳定性分析中的应用[J]. 中国海洋平台,2008(4):18-22.
Song Yanxin,Yang Qing,Tang Xiaowei,et al. The application of ABAQUS secondary development in the stability analysis of submarine pipelines[J].China Offshore Platform,2008(4):18-22(in Chinese).
