蚁群算法在PWM驱动系统EMC建模中的应用
2011-04-24刘金凤王旭东周美兰
刘金凤, 王旭东, 周美兰
(哈尔滨理工大学电气与电子工程学院,黑龙江哈尔滨150080)
0 引言
目前,脉冲宽度调制(pulse width modulation,PWM)电机驱动控制系统因为具有良好的运行特性,已经在工业和民用装置中得到了广泛应用,但是他所带来的电磁干扰(electromagnetic interference,EMI)问题也日趋严重。PWM调制过程中产生的电压变化率可达到5~15 kV/μs,由此产生的电磁干扰是对PWM系统电磁兼容性能的巨大考验。近年来,许多学者都进行了PWM驱动系统传导干扰特性的研究,文献[1-2]利用仿真软件建立了PWM系统的仿真模型,通过时域和频域两种方法进行模型的验证,但是由于这些模型没有考虑到干扰源的高频模型,所以其模型仅适合1 MHz的低频段。文献[3-4]采用实验测试和理论计算相结合的方式进行系统建模,该计算求解过程缓慢,同时存在大量的假设和简化,并不能反映真实寄生参数在高频干扰作用下所带来的影响。
本文以他励直流电机的PWM驱动系统为研究对象,通过深入分析系统高频特性,建立系统的电磁兼容(electromagnetic compatibility,EMC)模型,对于参数的确定采用实验与蚁群算法相结合的方式,即先利用阻抗分析仪得到系统的阻抗频率特性,再建立模型参数的向量集合,利用蚁群算法进行参数的快速智能搜索和优化,直到满足精确度要求,最后输出该算法所选取的电路模型参数。
1 PWM驱动系统的干扰传播通道
控制系统目前多采用脉冲宽度调制斩波方式,即对主电路系统采用降压或升压斩波技术,实现对直流电机的控制。二象限直流斩波电路作为一套直流电机的控制电路,复合了降压和升压斩波技术,使其既适用于驱动直流电机模式,又适用于再生制动模式。
经过国内外学者对PWM系统的传导干扰的大量研究发现,因为共模和差模传导干扰的形成机理、耦合路径等都不尽相同,所以需要分开研究。通过对PWM系统的电磁干扰特性进行分析得出结论:由于电路本身存在的寄生参数为共模传导干扰的传播提供了丰富的传播路径,导致共模电流会通过对地的寄生参数流入其他系统并对其产生影响,所以,共模传导干扰的危害要远远大于差模干扰,共模干扰成为PWM系统干扰的主要成分和抑制对象[5-6]。
图1为PWM驱动系统工作时,采集的MOSFET开关管漏源极之间电压变化的时域波形,开关管每次通断时,都会产生瞬态的电压尖峰。
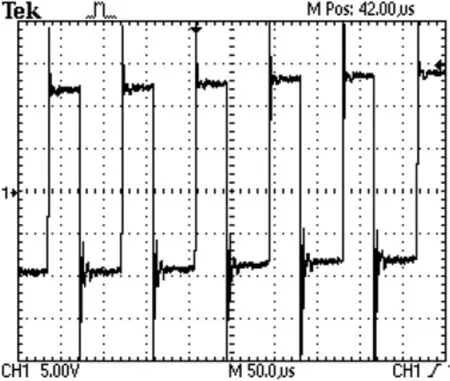
图1 开关管端电压时域波形Fig.1 Time domain wave of switch terminal voltage
图2为在电磁兼容实验室测量得到的开关管对地产生共模电流的时域波形。由图2可知,开关管在每次通断瞬间都会形成强烈的共模干扰电流,于是形成系统的干扰源。为了检测系统中存在的共模传导干扰频谱,需要在直流侧串入线性阻抗稳定网络 (line impedance stabilization network,LISN)。LISN有两个作用:一是可以为被测设备提供稳定的50 Ω接地阻抗用以保证测试结果的可比性;二是减小电网干扰对测试结果造成的影响。

图2 共模电流时域波形Fig.2 Time domain wave of common mode current
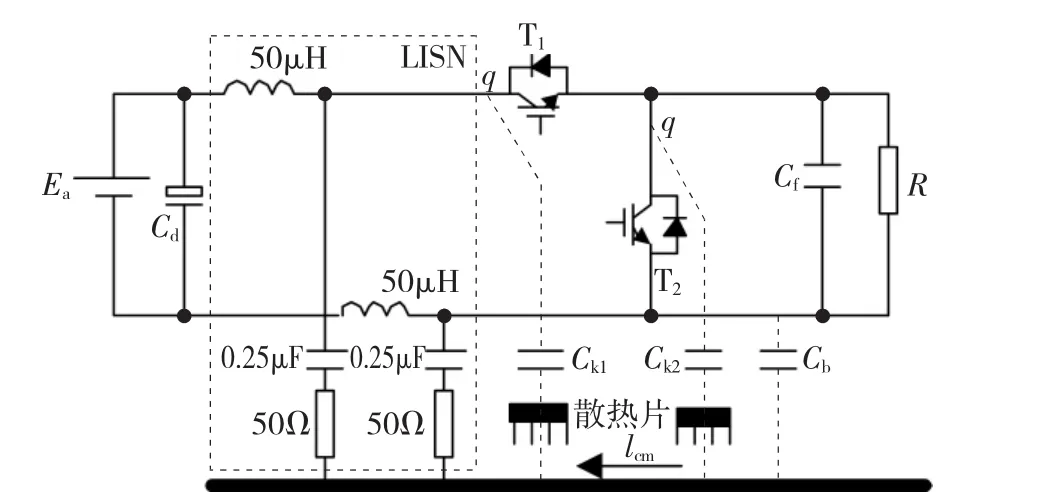
图3 PWM变换器传导干扰传播通道Fig.3 Conducted interference coupling paths of PWM converter
PWM驱动控制系统共模传导干扰传播路径如图3所示,引起共模电流的原因是由于开关管漏极与散热器之间形成很大的高频寄生电容Ck,当开关管通断时,由于变换器q点存在寄生电容导致该点对参考地的电位不停地发生变化,这个变化的电位对寄生电容进行充放电,引起共模电流。共模电流流过寄生电容Ck1和Ck2,再经过散热器到达参考地,然后再通过LISN的50 Ω电阻和0.25 μF电容回到直流侧。同时系统直流母线对地也存在寄生电容Cb,为共模电流提供了丰富的传播路径[7-8]。
图4为PWM驱动控制系统的电源端串接LISN后,通过电磁干扰接收机观察规定的50 Ω阻抗上存在的共模传导干扰的频谱。

图4 实测共模干扰频谱Fig.4 Measured result of common mode interference spectrum
由图4可知,该系统在0.7~6 MHz之间的共模干扰超过国际A类标准的限制,不满足电磁兼容标准EN55022的要求。
2 PWM驱动控制系统共模干扰模型分析
2.1 共模干扰电压源分析
由于对电气装置的电磁兼容问题进行分析时,通常是考察电磁干扰的频谱幅值特性,而且EMC标准所规定的限值也是以频谱幅值形式给出的,所以就需要对PWM驱动控制系统共模电压进行频谱分析。
根据参考文献[9],PWM变换器的共模干扰电压源表达式为
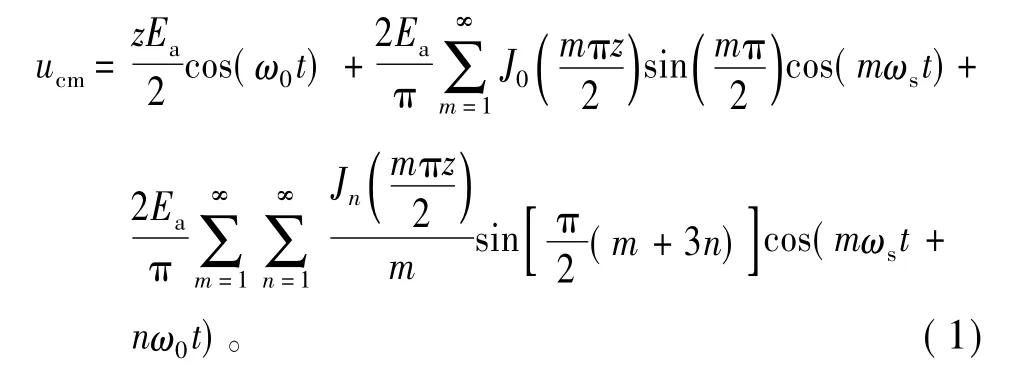
式中:ucm为变换器输出的共模电压;z为调制比;Ea为正负直流母线电压;ω0为调制波角频率;ωs为载波角频率;J0和Jn分别为0阶和n阶贝塞尔函数,根据公式性质,这里的贝赛尔函数全部采用第一类贝赛尔函数。
但是该频谱模型没有考虑开关管开关信号的上升时间。假设上升时间tr与下降时间tf相等,则开关信号的幅值频谱为

式中fs=ω0/(2π),而优化函数β(fs)是由共模电压时域信号的上升时间来决定的。在该电机驱动控制系统中,开关信号幅值 A=3.3 V,占空比 α=0.5,IPB180N04S3型开关管上升时间tr=54 ns,开关频率fs=10 kHz,将参数代入式(4),于是计算得到优化函数的值为0.017。
2.2 高频等效电路模型分析
根据图3对PWM驱动控制系统的传导干扰分析,建立的PWM驱动控制系统高频等效电路模型如图5所示,其中电压源ucm1和ucm2分别为主回路开关管和续流开关管两端高频共模干扰电压源。

图5 PWM系统高频EMC模型Fig.5 High frequency EMC model of PWM system
在研究高频共模干扰电流时,直流侧和负载侧滤波用电容Cd和Cf对高频信号近似于短路,于是直流电源被认为短路,同时在正负直流母线侧接入的LISN在共模通道中可以等效成两条支路的并联,即等效成 0.5 μF 电容、25 μH 电感和 25 Ω 电阻。Lk1和Lk2分别为主回路和续流回路开关管的散热器与参考地连接线之间的等效电感,Ck1和Ck2分别为主回路和续流回路开关管漏极对参考地的等效寄生电容,Cb为直流母线正负极对参考地的等效寄生电容。
3 蚁群算法
蚁群算法(ant colony algorithm,ACA)是对自然界蚂蚁的寻径方式进行模拟而得出的一种仿生算法。蚂蚁个体之间是通过在其所经过的路上留下一种称为“信息素”(pheromone)的物质来进行信息传递的。信息素可以理解为个体之间相互影响的一个正反馈机制,信息素越多的路径吸引的蚂蚁越多,最终实现最优路径的选择,这就是蚁群算法的基本原理。蚁群算法有两个重要特征,其一是蚂蚁在群体觅食过程中所体现出来的正反馈过程,在这个过程中,通过反馈机制的调节,可以对系统的较优解起到一个自增强的作用,从而使问题的解向着全局最优的方向进行,并能获得全局的相对最优解;另一特征是分布式并行计算能力,算法可以在全局的多点同时进行解的搜索,从而避免了陷入局部最优解的可能[10]。
3.1 ACA算法基本原理
假定有h个待优化的参数,记为P1,P2,…,Ph,对于其中任一参数Pi(1≤i≤h),将其设置为可能取值范围内的N个随机非零数,形成一个集合QPi。全部蚂蚁从蚁巢出发去寻找食物,每只蚂蚁从集合QPi出发,根据集合中每个元素的信息素τj(QPi)和状态转移概率,独立随机地从每个集合QPi中唯一地选择一个元素。状态转移概率和信息素的计算分别根据式(7)和式(8)计算得到,即
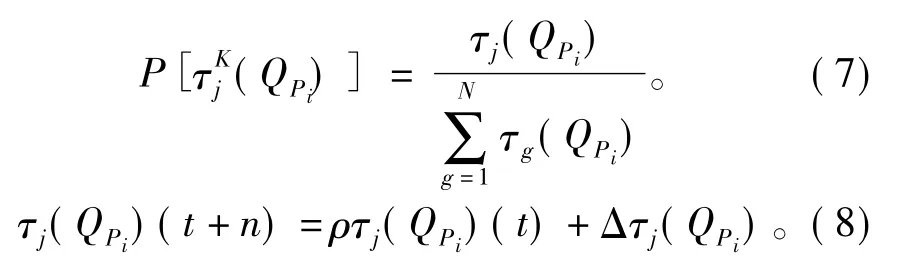
式中:τj(QPi)(t)为在第t时刻留在集合QPi的第j个元素上的信息素;τj(QPi)(t+n)为在经过n时刻留在集合QPi的第j个元素上的信息素;ρ为残留信息的持久程度,则1-ρ为信息的挥发程度;Δτj(QPi)为蚂蚁在本次循环中留在集合QPi的第j个元素上的信息素增量,他是所有蚂蚁在该元素上信息素增量的和,该增量的计算取决于算法计算输出与实际输出的偏差,偏差越小,信息素增加的就越多。当蚂蚁在所有集合中完成元素的选择后,他就到达了食物源,此后按一定规则调节集合中各元素的信息素。这一过程被反复进行,直至找到最优解或达到给定的迭代次数而停止搜索。
3.2 ACA算法参数选择
由ACA算法搜索路径的机理可知,算法中有关参数的不同选择对蚁群算法的性能有着至关重要的影响,但是算法参数的设置目前在理论上还没有依据,是通过反复匹配和调整后凭经验得到的。解空间规模N和蚂蚁组数K的设置与最优解的搜索效率、解的精确度,以及解的全局性等优化性能紧密相关。若问题的局部最优点较为密集,则可选择较大的N,K的选取与N直接相关,N越大,则所需的K就越大,但 K的选取还应考虑算法的时间复杂性[11]。残留信息持久度一般为 0.5≤ρ≤1,取 0.7左右为最佳;信息素总量Q一般取为1≤Q≤10 000,其值对算法的影响不大。由于Q比ρ的取值范围要大得多,所以实际调整中,可先随机设定ρ值后,再调整Q值,以得到较理想的解。在基本确定Q值后,再反过来调整ρ值,寻找更优的解。如此反复调整,最终逼近两参数的理想组合[12]。
3.3 ACA算法在PWM系统高频建模中的应用
由PWM电机驱动控制系统共模等效电路可知,由于系统采用的主回路和续流回路开关管为同型号、同批号的MOSFET管,同时开关频率相同,所以其寄生参数基本相同,包括开关管的漏极对参考地的寄生电容Ck和散热器对参考地的寄生电感Lk,于是为了减少算法的迭代次数,简化算法的参数选取过程,近似认为两管寄生参数相同。于是在该等效电路中需要利用蚁群算法确定3个参数,即开关管寄生参数Ck和Lk以及直流母线对地寄生参数Cb。在分析系统高频等效电路阻抗参数时,干扰源按短路分析计算,于是可得到如图5所示的高频等效电路阻抗计算的H函数为

根据电路和开关管特性可以设置蚁群算法所需输入,即等效电路参数的候选解数组(3×30,3个待选等效电路参数,每个参数根据经验计算得到30个待选解)。蚁群算法参数设置为:最大循环次数Nc=200;蚂蚁数目K=100;信息素总量Q=700;残留信息持久度ρ=0.7;偏差量E控制在0.1以内。初始时刻信息素增量设置为零,即所有蚂蚁都置于蚁巢中,其算法流程如图6所示。每只蚂蚁根据状态转移概率来决定解空间的选取,再将每只蚂蚁选择的电路参数带入到阻抗的H函数计算式中统计出矢量系数,然后利用freqs()函数计算矢量系数构成的模拟滤波器的幅频输出响应,该函数的频率范围为150 kHz~30 MHz。根据函数的计算输出与期望输出的偏差来更新每只蚂蚁的信息素,待所有蚂蚁都到达食物源以后,记录最优解的偏差,若偏差达到要求则停止计算,否则继续。若100只蚂蚁经过200次循环都没有达到精确度要求,则考虑算法是否适合该类问题的求解。

图6 蚁群算法确定电路参数流程Fig.6 Fixed circuit parameters flowchart by ACA algorithm
4 实验与仿真
4.1 实验论证
为了获得PWM系统的高频EMI模型,首先需要通过实验获得系统的阻抗幅频特性,然后将其等效为一个集总参数电路,使得在整个频段内的等效电路阻抗与实测绕组阻抗一致。电机阻抗测试采用安捷伦公司的Agilent 4249A型精密阻抗分析仪,他的扫描频率范围为40 Hz~110 MHz,覆盖了本文所要研究的传导干扰频段。采用静态测量方法,即主回路电源断路,测量门极在高速开关信号控制作用下,所产生的对地高频阻抗频率特性。图7为PWM驱动控制系统的阻抗频率特性。由阻抗分析仪得到的阻抗频率特性曲线可知,开关管对地确实存在引起共模干扰的对地寄生参数,这些参数所组成的阻抗频率特性呈现电容特性。在扫频频率达到20 MHz左右时,其阻抗输出值达到最小,接近600 Ω左右,并趋于稳定。

图7 PWM驱动控制系统阻抗频率特性Fig.7 Impedance frequency characteristics of PWM driving control system
4.2 等效电路参数仿真分析
为了获得等效电路参数,需要利用图7中阻抗分析仪得到的阻抗频率特性关系,将该频率特性关系输入到Matlab的蚁群算法输入端口,作为蚁群算法进行参数选择的基准,每只蚂蚁根据信息素和状态转移概率从候选解数组中选取3个等效电路参数后带入到式(9)的H函数中,再通过freqs函数计算幅频响应,与阻抗分析仪得到的基准值进行比较,直到满足精确度要求完成参数选择,利用蚁群算法进行参数集合的优选,其算法训练曲线如图8所示。

图8 蚁群算法训练曲线Fig.8 Training wave of ACA
由算法训练过程的仿真结果可知,采用蚁群算法进行电路仿真模型的参数选择时,训练步数不足20次就已经达到了0.1的仿真精确度,随着训练步数的增加,其精确度逐步趋于稳定。算法最终输出等效电路参数为:Ck=60.2 pF;Lk=1.8 μH;Cb=193 pF。
图9为实测阻抗频率特性与仿真输出阻抗频率特性对比图,由图9可见,在整个EMC频段内,仿真曲线较好地再现了实测曲线。

图9 仿真与实测阻抗频率特性对比Fig.9 Comparison of simulation and experiment for impedance frequency characteristics
4.3 PWM系统共模干扰仿真频谱分析
为了验证所建模型和干扰源分析的正确性,将干扰源分析和高频等效电路模型引入到PSPICE电路分析软件中,其仿真模型如图10所示。在研究高频共模干扰电流时,直流侧电容Cd对高频信号近似于短路。在正负直流母线侧接入的LISN在共模通道中可以等效成两条支路的并联,即等效成0.5 μF电容和25 Ω电阻。直流电源被认为短路,25 μH的电感来自于从LISN到直流侧电容的等效电感。
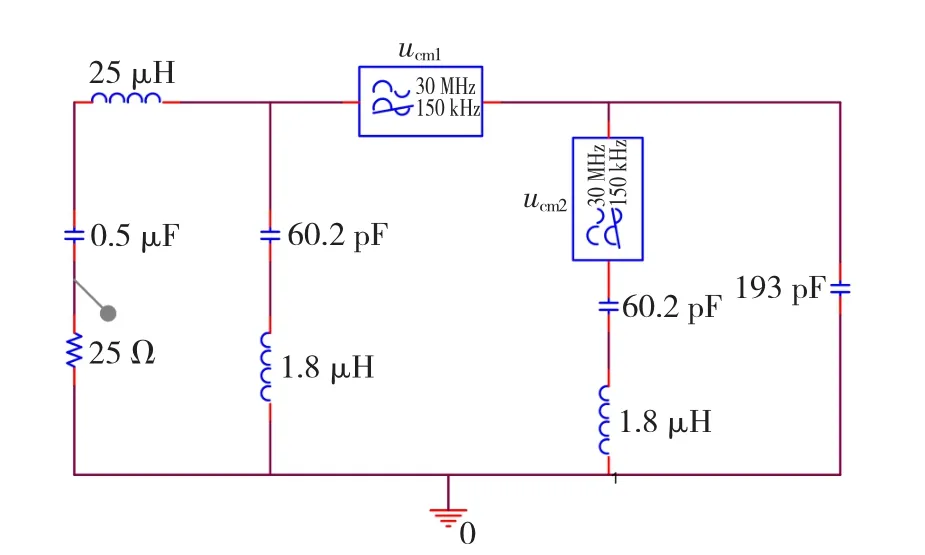
图10 电路仿真模型Fig.10 Model of circuit simulation
MOSFET的等效高频干扰源采用PSPICE中的行为仿真模型。从理论上讲,所有有源器件皆可转化为含受控源的等效电路进行分析,仿真行为模型就是电路仿真软件的受控源中的新成员。在PSPICE中有4种理想受控源:电压控制电压源;电流控制电流源;电压控制电流源;电流控制电压源。这几种受控源具有输入阻抗无限大、输出阻抗为零、带宽无限大、任何工作环境下增益为定值等完全理想化的特性。而仿真行为模型则是可以根据用户的需要,调整其输入输出转移特性曲线,幅频、相频特性曲线,因此他会产生更加逼真的描述谐波失真、带宽受限等非理想特性[13-14]。仿真行为模型是电压控制电压源和电压控制电流源型受控源的延伸,他们都是利用数学运算方式描述的,常用的行为模型皆存在于ABM.olb库中。将前面分析得到的PWM变换器的共模电压幅频特性输入到该模型中,作为仿真系统的受控源。同时在代表LISN的25 Ω电阻的上端口设置一个测量电压频谱的Probe探针,然后在仿真设置窗口中设置分析类型为交流分析,并将扫描频率范围设置在150 kHz~30 MHz范围内。
图11为利用PSPICE电路仿真软件得到的LISN侧共模电压在整个传导干扰频段(150 kHz~30 MHz)的仿真频谱图。

图11 驱动控制器共模传导干扰频谱Fig.11 Spectrum of common-mode conducted EMI in drive controller
从该仿真频谱中可以看出,直流电机的PWM驱动控制系统在工作过程中存在对地的共模传导电磁干扰,特别是在500 kHz~3 MHz的频率范围内,系统的共模传导电磁干扰的强度高于直流电机单独工作过程中的共模干扰强度,证明功率开关管在工作过程中的共模干扰加载到了直流电机中,导致整个系统的共模干扰强度已经超过了国际电磁兼容的A类标准。
图12为利用PSPICE电路仿真软件得到的LISN侧共模电压在不同频段的仿真频谱与实验频谱对比图。由仿真和实验的共模干扰频谱对比图可知,利用蚁群算法建立的等效电路模型较好地反映了高频共模干扰的实验频谱,也充分证明了所建模型的正确性。

图12 驱动控制系统共模干扰仿真与实验频谱对比Fig.12 Comparison of simulation and experiment for drive controller common mode interference
5 结语
为了弥补目前PWM驱动控制系统高频等效电路模型中的缺陷,采用蚁群算法来确定等效电路模型中的参数,算法不仅训练速度快,而且仿真精确度高。通过Matlab仿真结果与阻抗分析仪的阻抗测试实验结果的对比,以及PSPICE电路仿真结果与LISN的共模干扰频谱结果的对比,证明了基于蚁群算法的PWM驱动控制系统的高频仿真模型的准确性较高,能够实现系统电磁兼容性能的预测,为后续电磁干扰的抑制奠定了基础。
[1] 姜保军.PWM电机驱动系统传导共模 EMI抑制方法研究[D].哈尔滨:哈尔滨工业大学电气工程及自动化学院,2007:53-57.
[2] 单潮龙,马伟明,王铁军,等.逆变器驱动电机系统EMC模型建立及直流侧传导干扰研究[J].海军工程大学学报,2003,15(1):1-6.SHAN Chaolong,MA Weiming,WANG Tiejun,et al.Conducted EMI analysis and modeling of DC power supply with an inverter load[J].Journal of Naval University of Engineering,2003,15(1):1-6.
[3] MOREAU Maxine,IDIR Nadir,LE MOIGNE Philippe.Modeling of conducted EMI in adjustable speed drives[J].IEEE Transactions on Electromagnetic Compatibility,2009,51(3):665-672.
[4] LAI J S,HUANG Xudong,PEPA Elton,et al.Inverter EMI modeling and simulation methodologies[J].IEEE Transactions on Industrial Electronics,2006,53(3):736-744.
[5] HAMZA Djilali,JAIN Praveen K.Conducted EMI noise mitigation in DC-DC converters using active filtering method[C]//PESC'08-39th IEEE Annual Power Electronics Specialists Conference,June 15-19,2008,Rhodes,Greece.2008:188-194.
[6] 孟进,马伟明,张磊,等.PWM变频驱动系统传导干扰的高频模型[J].中国电机工程学报,2008,28(15):141-145.MENG Jin,MA Weiming,ZHANG Lei,et al.High frequency model of conducted EMI for PWM variable-speed drive sytems[J].Proceedings of the CSEE,2008,28(15):141-145.
[7] AGGELER Daniel,BIELA Juergen,KOLAR Johann W.Controllable dv/dt behaviour of the SIC MOSFET/JFET cascode an alternative hard commutated switch for telecom applications[C]//25th Annual IEEE Applied Power Electronics Conference and Exposition,February 21-25,2010,Palm Springs,USA.2010:1584-1590.
[8] FUNAKI Tsuyoshi,ARIOKA Hisato,HIKIHARA Takashi.The influence of parasitic components on power mosfet switching operation in power conversion circuits[J].IEICE Electronics Express,2009,6(23):1697-1701.
[9] 裴雪军.PWM逆变器传导电磁干扰的研究[D].武汉:华中科技大学电气与电子工程学院,2004:34-37.
[10] 苏文海,姜继海,刘庆和.直驱式电液伺服转叶舵机退火蚁群寻优 PD 控制[J].电机与控制学报,2010,14(1):102-106.SU Wenhai,JIANG Jihai,LIU Qinghe.PD controller based on simulated annealing ant colony optimization algorithm in direct drive electro-hydraulic servo rotary vane steering gear[J].Electric machines and control,2010,14(1):102-106.
[11] JENNINGS Alan L,ORDÓÑEZ Raúl,CECCARELLI Nicola.An ant colony optimization using training data applied to UAV way point path planning in wind[C]//2008 IEEE Swarm Intelligence Symposium,September 21-23,2008,Saint Louis,USA.2008:4668302.
[12] 王旭东,刘金凤,张雷.蚁群神经网络算法在电动车用直流电机起动过程中的应用[J].中国电机工程学报,2010,30(24):95-100.WANG Xudong,LIU Jinfeng,ZHANG Lei.Application of ant colony algorithm neural network in the starting process of DC motor used in electric vehicle[J].Proceedings of the CSEE,2010,30(24):95-100.
[13] BIOLEK Dalibor,BIOLEK Zdenek,Biolková Viera.PSPICE modeling of meminductor[J].Analog Integrated Circuits and Signal Processing,2011,66(1):129-137.
[14] BEN HADJ SLAMA Jaleleddine,HRIGUA Slim,COSTA Francois,et al.Relevant parameters of SPICE3 MOSFET model for EMC analysis[C]//2009 IEEE International Symposium on E-lectromagnetic Compatibility,August 17-21,2009,Austin,USA.2009:319-323.
