挠性高稳定度卫星载荷扰动力矩补偿研究

赵江涛，李 果

(1.北京控制工程研究所，北京 100190;2.中国空间技术研究院，北京 100094;3.空间智能控制技术重点实验室，北京 100094)

有效载荷高分辨率观测，要求卫星平台的指向精度和姿态稳定度.针对某些三轴稳定卫星，尽管观测时间可连续，但为扩大观测视场，提高空间观测范围，有效载荷相对卫星平台运动.而相应的扰动力矩影响平台的指向精度和姿态稳定度.

文献［1-3］针对GEOS I～M系列气象卫星的扫描镜扰动，研究并采用基于载荷和星本体动力学模型的运动补偿.文献［4-6］针对GEOS N～Q系列气象卫星的扫描镜扰动，提出并采用基于姿态测量信息的运动补偿.主要方法:根据星体的姿态(由动力学估计或敏感器测量)修正运动有效载荷的运动量，进而提高载荷的指向精度.但要求精确的载荷与星体相互作用的动力学模型，或者要求高精度、高带宽的姿态敏感器，且平台稳定度很差.

文献［7-8］针对带红外扫描相机和红外凝视相机的预警卫星，提出前馈控制姿控动量轮补偿扰动的方法.针对载荷扰动力矩大于动量轮的最大输出力矩，且扫描相机扰动具有周期性，前馈补偿控制器输出延时一个扫描周期，且使动量轮输出力矩脉冲的中心和扫描相机干扰力矩脉冲的中心重合.该方法对凝视相机的扰动无效，并且补偿效果反比于载荷扰动力矩和动量轮最大输出力矩的比值.

文献［9］针对带运动天线或机械手的卫星提出一种利用动量轮的自适应补偿方法.针对动量轮与有效载荷的响应时间不同，提出超前或滞后校正，但针对大扰动力矩补偿效果不明显.

文献［10］对新一代气象卫星的载荷扰动补偿问题进行了研究，但力矩前馈补偿的执行机构建模为一阶惯性环节，未深入研究执行机构的问题，如摩擦力矩.

本文研究利用专门的补偿机构，补偿有效载荷的大扰动力矩，对其摩擦力矩和输出力矩延迟设计了补偿控制律，并前馈控制偏航轴动量轮以满足5×10－4(°)/s(3σ)的高稳定度要求.

1 系统仿真平台

建立卫星的姿态仿真系统，以验证力矩前馈补偿的效果，包括姿态反馈控制和帆板转动驱动.

1.1 动力学方程

根据拟坐标下的拉格朗日方程［11］推导含4个动量轮(3个正交一斜装)、2个补偿机构、2个大扰动力矩运动有效载荷和2个大型挠性帆板的卫星动力学方程为

挠性太阳帆板转动动力学方程:

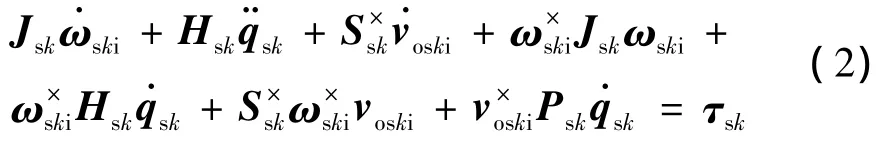
挠性太阳帆板振动动力学方程:

刚性附件转动动力学方程:

1.2 动量轮模型

姿态控制的执行机构为动量轮，其近似传递函数为

其中Tw为动量轮的时间常数，取Tw=0.1 s/rad.

1.3 姿态控制器

忽略帆板的挠性及各轴间的耦合作用，各通道均可视为双积分环节.按照如下方法计算PID的控制参数［10］:

其中BW为系统带宽，取0.1Hz.以滚动通道为例，考虑动量轮时PID和PD控制的Bode图如图1所示.

图1 滚动通道PID和PD控制bode图

当增益为 －3dB时，角频率为0.654rad/s，即0.104Hz，均满足带宽要求.但PID的积分环节引入一个s=－0.0217的极点，易使系统不稳定.因此，选择该方法计算的PD控制器.

1.4 SADA细分驱动

太阳帆板对日定向，需要相对卫星平台转动.某些卫星平台一般由间接驱动型SADA驱动太阳帆板，取步进电机的步进角为1.8°，步进周期为4.32s，减速箱减速比为N=100∶1.

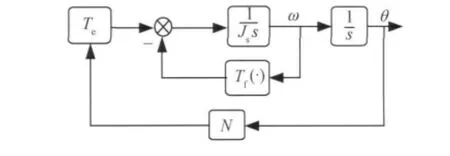
图2 帆板驱动系统结构框图

图中，

表1 SADA各参数的意义以及取值

由图3(K=4时，未细分)可见，帆板每次步进均为一振荡衰减过程，相应的扰动力矩较大且高频振荡.为减小SADA对卫星平台的扰动，利用正余弦细分驱动原理［12］对SADA细分.

细分数K从理论上讲可为任意正整数，但实际频率控制由分频电路产生，实际应用中K取2n.对不同K值进行仿真，结果如图3所示.

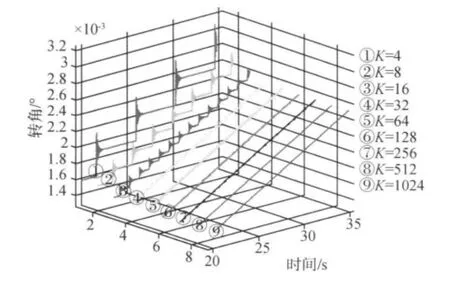
图3 K不同取值时转角时间关系曲线

当K=8、16、32 时(步进角 2、4、8 细分)振荡逐渐减弱，扰动力矩相应减小;K=256、512、1024时转角的高频振荡基本消失，扰动力矩非常小.

当K=512时，仿真得平台的姿态稳定度为2.44 ×10－4(°)/s(3σ)，优于指标 5 × 10－4(°)/s(3σ).因此，此仿真平台可验证补偿效果并确定能否满足姿态稳定度要求.

2 力矩补偿原理及补偿控制律设计

2.1 力矩补偿原理

力矩前馈补偿原理:根据有效载荷的运动规律，前馈控制补偿机构以补偿有效载荷扰动.其框图如图4所示.

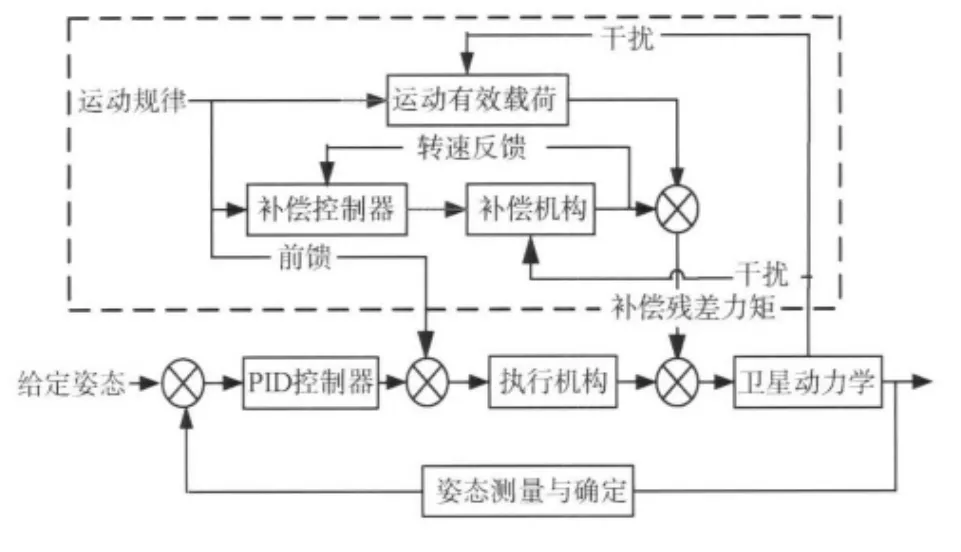
图4 前馈补偿结构框图［10］

其中扫描型运动的有效载荷(假设为扫描相机)和定标型运动的有效载荷(假设为凝视相机)的运动规律如下:

扫描相机工作时沿滚动轴进行南北方向的一维线阵扫描，加减速阶段均为正弦规律.凝视相机随常平架(外框)东西方向转动到指定位置，再由指向镜完成南北方向的扫描，加减速过程均按1/4正弦规律.相应的扰动力矩如图5所示.

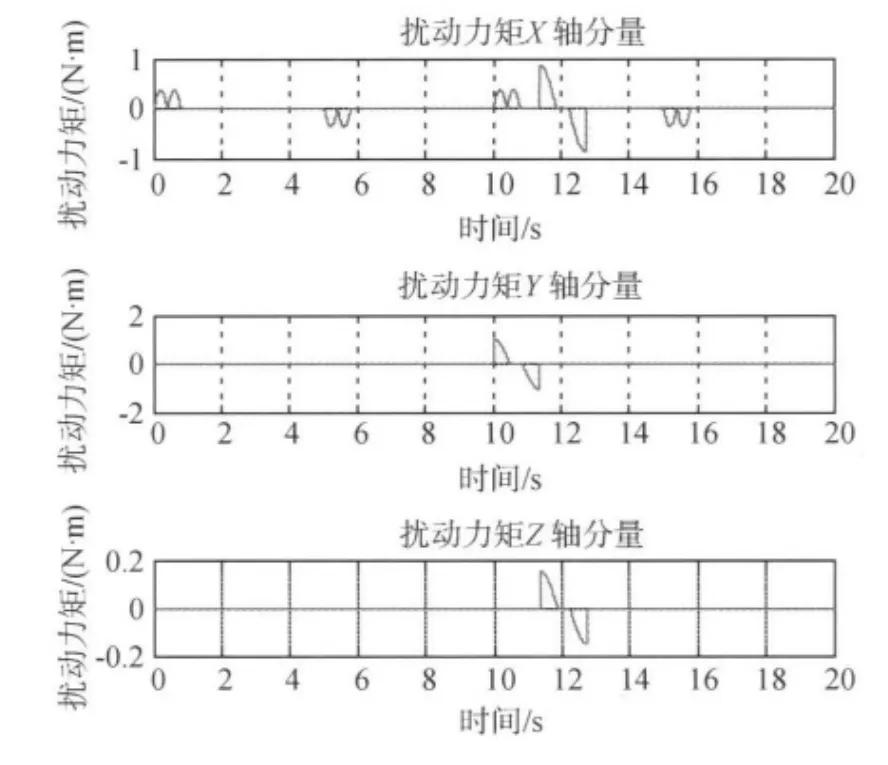
图5 有效载荷扰动力矩曲线

力矩补偿所用的补偿机构最大输出力矩1.6 N·m，工作于反作用状态，忽略其限速和反馈电动势饱和问题.其仿真模型框图如图6所示.

图6 补偿机构仿真模型框图

补偿机构仿真模型的状态方程为:

但补偿机构的摩擦力矩和输出力矩延迟影响补偿机构力矩输出特性，并且在无载荷扰动时引入摩擦力矩扰动，需设计补偿控制律，以提高补偿效果.

2.2 补偿控制律设计

针对补偿机构可供反馈的信号只有其转速的特点，提出基于参考模型的转速闭环补偿方法，其方框图如图7所示:

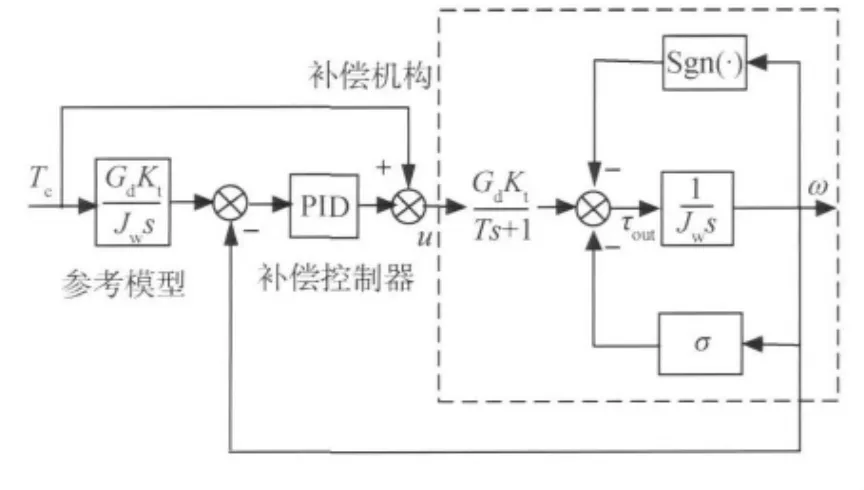
图7 基于参考模型的转速闭环补偿控制律

表2 补偿机构各参数的意义及取值

其中，摩擦力矩建模为库仑摩擦+粘滞摩擦模型，且库仑摩擦视为常值扰动.此时从输入指令到输出力矩的传递函数:

实际应用中，测量存在噪声且补偿机构存在力矩波动，微分对噪声起放大作用，影响补偿性能.因此，在PID控制环节处加一低通滤波器，形式如:

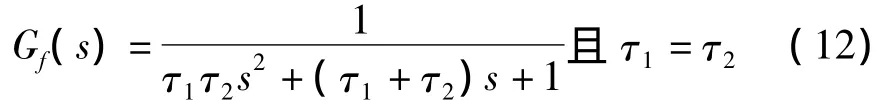
带滤波器的传递函数为

此处:Kp=35，Ki=40，Kd=0.5，τ1=τ2=0.00097.

加入滤波器前后的系统bode图如图8所示.可见，加入滤波器使系统在1.25Hz左右的相角超前特性略有增加，但可忽略;幅值基本没影响，即对系统所需频率的影响可忽略.

加入滤波器前补偿机构的闭环极点:

s1= －145.3701，s2= －86.0696，s3= －1.1675.

加入滤波器后:

s1= －1400.4，s2= －80.4，s3= －1.167，s4= －315.0+137.7i，s5= －315.0 －137.7i.

可见，加入滤波器对系统的动态性能影响很小，但可明显滤除由微分带来的补偿量噪声.

补偿控制律的补偿效果仿真如下所示.

可见，补偿控制律能够较好的补偿摩擦力矩和输出力矩延迟.

2.3 偏航轴前馈控制

凝视相机启动时扰动力矩耦合至偏航轴，而仅依靠该轴动量轮的反馈控制，由于带宽和最大输出力矩等原因补偿不及时.因此，利用前馈力矩补偿［7］，将凝视相机的运动规律前馈至该动量轮，以更及时的补偿扰动.但动量轮响应时间、幅值受限及扰动的快速性决定不能采用比例前馈，特采用如下的前馈律:

其中，Tzc为偏航轴动量轮前馈补偿指令力矩，τlz为凝视相机偏航轴耦合扰动力矩.

3 力矩补偿效果仿真

采用上节的补偿控制律和补偿机构补偿载荷扰动，扫描相机按规律运动，凝视相机在20s时启动，目标转角为(10°，10°)，帆板初始转角为0°，仿真结果如下:

由中心刚体姿态角曲线和角速度曲线得补偿效果如表3所示.分析帆板模态坐标曲线易得，凝视相机启动引发第一、二、四、五阶模态较强的振荡，但第一阶为主.帆板基本呈匀速转动，扰动力矩较小.

对比各轴的稳定度和指向精度发现，各轴均可满足稳定度要求，但凝视相机启动时偏航轴稳定度为4.81 ×10－4(°)/s，不满足稳定度要求.对比偏航轴动量轮输出力矩和载荷扰动力矩偏航轴分量可见，动量轮由于幅值受限和响应时间原因，前馈补偿效果不理想.

因此，借鉴补偿机构设计技术，改进偏航轴动量轮，修改电机结构以提高其最大输出力矩至0.3 N·m，改进驱动控制以降低响应时间至60ms.偏航轴动量轮改进后，稳定裕度增加，不必重新设计控制器.前馈力矩指令正比于耦合力矩，重复上述仿真，结果如图10中a)、b)和c)的曲线所示.

偏航轴前馈补偿结果如表3所示，与改进前相比，偏航轴稳定度提高近六倍，指向精度提高近九倍，不再是稳定度和指向精度的瓶颈.凝视相机启动时偏航轴稳定度为0.79 ×10－4(°)/s，仍满足稳定度要求.

表3 偏航轴前馈补偿的补偿效果

因此，此力矩补偿方法有效，且补偿效果明显.并且，SADA扰动已为卫星平台的稳定度的主要限制因素.

4 结论

本文针对卫星平台高稳定度的要求，对帆板驱动机构(SADA)进行正余弦细分，并运用专门的力矩补偿机构补偿运动有效载荷的大扰动力矩.针对补偿机构的摩擦和延迟设计了补偿控制律.对于偏航轴，改进偏航轴动量轮并前馈控制以实施力矩补偿.由仿真结果可以看出，力矩补偿后的姿态稳定度优于5 ×10－4(°)/s(3σ)的指标要求.

［1］ Kamel A A，Bhat M K P，Gamble D，et al.GEOS I～M image motion compensation system［C］.AIAA Aerospace Design Conference，Irvine CA，Feb.3-6，1992

［2］ Peter Y C.Slew disturbance compensation for multiple spacecraft payload［C］.ASS/AIAA Astrodynamics Specialist Conference，Stowe VT，Aug 7-10，1989

［3］ Yu Z F，Yang Z C.Analysis of scan mirror motion and its compensation for three-axis-stabilized satellite［J］.Key Engineering Materials，2003，243-244:93-98

［4］ Markley F L，Bauer F H，Deily J J，et al.Attitude control system conceptual design for geostationary operational environmental satellite spacecraft series［J］.Journal of Guidance，Control and Dynamics，1995，18(2):247-255

［5］ Mark D M，Peter Y C.Slew disturbance compensation for multiple spacecraft payloads of a flexible spacecraft［C］.AIAA Guidance，Navigation and Control Conference，Hilton Head Island，SC，Aug 10-12，1992

［6］ Advanced Missions Analysis Office Goddard Space Flight Center.Geostationary Operational Environmental Satellite(GOES-N Report)Technical Appendix.Volume 2［R］.PB92-147123，1991

［7］ 魏世隆，曹喜滨，张世杰.具有运动部件的预警卫星姿态前馈复合控制［J］.航天控制，2004，22(3):45-49

［8］ 张世杰，曹喜滨.跟踪弹道导弹时预警卫星姿态前馈协同控制［J］.飞行力学，2004，22(3):57-60

［9］ Katsuhiko Y，Shoji Y.Adaptive attitude control for an artificial satellite with mobile bodies［J］.Journal of Guidance，Control and Dynamics，1996，19(4):948-953

［10］ 陈守磊.带运动有效载荷卫星的补偿控制研究［D］.北京:北京控制工程研究所，2007

［11］ Leonard M.Hybrid state equations of motion for flexible bodies in terms of quasi-coordinates［J］.Journal of Guidance，Control and Dynamics，1991，14(5):1008-1013

［12］ 斯祝华.帆板驱动对卫星姿态的影响及姿态控制方法研究［D］.北京:北京控制工程研究所，2010