基于多输入多输出特征模型的高超声速飞行器自适应姿态控制*

王 勇，龚宇莲，王丽娇

(1.北京控制工程研究所，北京 100190;2.空间智能控制技术重点实验室，北京 100190)

本文所研究的类X-20飞行器是参照美国的X-20飞行器为原型构造的研究对象，由升降舵、方向舵和副翼3个舵面进行控制.此类航天器一般自80km处开始再入，最后水平着陆，突出特点是飞行包络线范围大(高度可达100km，速度可达20多马赫)，很难用单一的运行环境来描述高超声速流场.与亚声速和超声速飞行器相比，高超声速飞行器的运行环境要复杂的多，会受到许多因素的影响，主要包括动压效应、粘性效应、强/弱真实气体效应、低密度效应、机体表面辐射等［1］.其主要气动特性包括以下几个方面:气动弹性［2］、高超声速的影响、机体/推进力/结构动力学互相作用［3-4］、数据库的不确定性和速度变化较大的影响等.以上诸多问题都为控制器的设计提出各种挑战，在高超声速条件下，现有的制导与控制技术已经难以完全适用.对控制器设计的影响总结起来主要包括如下几个方面:

1)耦合的影响:主要包括3个控制通道的耦合和飞行姿态/气动力耦合.一般的飞行器主要考虑控制通道的耦合，而对于高超声速飞行器，由于飞行器姿态影响气动参数，气动参数的变化又引起气动力和力矩的变化，反过来导致飞行器姿态变化，因此在高超声速飞行过程中必须考虑姿态对气动力的影响.在飞行器动力学模型中具体体现在姿态动力学、运动学方程中3个姿态角及角速度的耦合，质心动力学方程中速度、攻角与侧滑角的耦合，气动力、力矩中3个输入舵偏角的耦合和姿态对气动参数的耦合.

2)较大的外部随机扰动和大范围变化的气动参数的影响:主要体现在对临近空间、高超声速条件下气动数据库的不确知性.由于临近空间的特殊性，无法在地面风洞进行有效的模拟实验，很难建立较为完备的气动数据库.而在大范围的飞行过程中，相对于再入点大气密度变化约10000倍，气流的变化也比较剧烈，因此控制器必须有足够的鲁棒性.

3)强非线性、强时变的影响［5］:高超声速飞行器对于飞行条件的变化是非常敏感的.高超声速条件下，攻角变化对系统过载影响很大，且存在大攻角舵效耦合带来的时延非线性动态特性问题，这些非线性因素给控制系统的设计带来非线性控制和解耦合等方面的问题.

根据文献［5］，高超声速飞行器须着重解决控制变参数、实时性等问题，进一步提高导航、制导精度，更好地协调高超声速飞行器快速性与稳定性之间的矛盾，提高高超声速飞行器可控性和抗干扰能力.

2010年4月22日，美国发射的HTV-2再入滑翔飞行器发射9min后失败，飞行异常的特点是“沿着纵轴缓慢偏转，直到翻滚速度达到极限值，触发自主飞行系统命令飞行中止”.分析认为:“飞行过程对若干空气动力学的关键参数认识有限［6］”.以上案例充分说明在高超声速条件下对于耦合与气动特性认识的不足导致控制失效.

针对以上问题，国内外学者在鲁棒控制、自适应控制、滑模变结构、神经网络逼近动态逆、增益调度及LPV控制等方面进行了许多尝试.文献［7］采用H∞/μ综合的方法对高超声速飞行器控制系统进行了设计.文献［8］通过线性分式变换(LFT)把线性变参数(LPV)方法用于X33姿态控制器的设计.文献［9］研究了自适应滑模控制器的应用，验证了跟踪指令速度的有效性，作者在对系统不确定性作了一定限制的假设下研究变结构控制器的设计.文献［10］应用动态逆方法研究了X-38再人大气层的姿态控制问题.由于神经网络具有强大的拟合作用，因此许多文献［11-13］采用神经网络来逼近动态逆，设计了各种自适应律进行姿态控制.国内学者也在以上领域进行了探索.李菁菁等［14］采用一种将自适应滑模变结构控制与动态逆控制组合的鲁棒自适应控制方法，用于临近空间高超声速飞行器的再入阶段飞行控制系统设计.黄显林等［15］针对一个吸气式高超声速飞行器模型，推导了LPV模型用于控制设计和开环分析，设计了以动压和马赫数为增益变量的飞行控制系统.周丽等［16］采用RBF神经网络在线逼近系统的不确定性及外界干扰条件下，提出了一种利用动态面控制技术简化回馈递推方法的控制律对空天飞行器进行姿态控制.

以上各种方法的突出特点是同时考虑鲁棒性和系统的时变性，采用鲁棒和自适应相结合的方法进行控制器设计，但由于原动力学模型非常复杂，以此为基础设计的控制器往往较为复杂，运算量大.而基于特征模型的全系数自适应控制，在原有动力学模型上提取输入输出主要关系，建立考虑控制要求的特征模型，然后在此基础上利用自适应控制器进行控制就会使得问题简化，而且设计出的控制器结构简单易于工程实现.

本文首先分析了系统的耦合关系，在此基础上基于特征建模的思想，采用分散控制的方式，在高超声飞行器六自由度模型的基础上得出了一个考虑输入耦合的特征模型，并采用黄金分割自适应的方法设计了控制器.针对大扰动和气动参数大范围变化这一难点，通过数值仿真验证了控制器在再入过程中、在气动参数变化较大和有风的条件下实现了很好的姿态跟踪，充分验证了该控制器应对以上问题的有效性.

1 高超声速飞行器动力学模型

主要符号说明:

m:飞行器质量(kg);

Ω =［ψ，θ，φ］T:偏航角，俯仰角，滚转角(rad);

α，β:攻角，侧滑角(rad);

V:飞行器质心速度(标量)(m/s);

g:重力加速度;

u，v，w:本体系下飞行器质心速度在三个坐标轴的投影(m/s);

ωb=［ωx，ωy，ωz］T:本体系相对于水平坐标系的转动角速度(rad/s);

ωe=［ωe，x，ωe，y，ωe，z］T:水平坐标系相对于地球惯性系的角速度(rad/s);

ρ:大气密度(kg/m3);

S，L:分别为飞行器参考面积和参考长度(m2，m);

F=［Fx，Fy，Fz］T:本体系下气动力 (N);

M=［Mx，My，Mz］T:本体系下气动力矩(N·m);

CF=［CF，x，CF，y，CF，z］T:沿轴向、侧向、法向气动力系数;

CM=［CM，x，CM，y，CM，z］T:滚动力矩系数，俯仰力矩系数，偏航力矩系数;

δ =［δe，δr，δa］T:升降舵偏角，方向舵偏角，副翼舵偏角 (°);

Jx，Jy，Jz，Jxz:本体系下转动惯量和惯量积.

1.2 质心动力学模型

高超声速飞行器本体系下质心动力学方程可写为

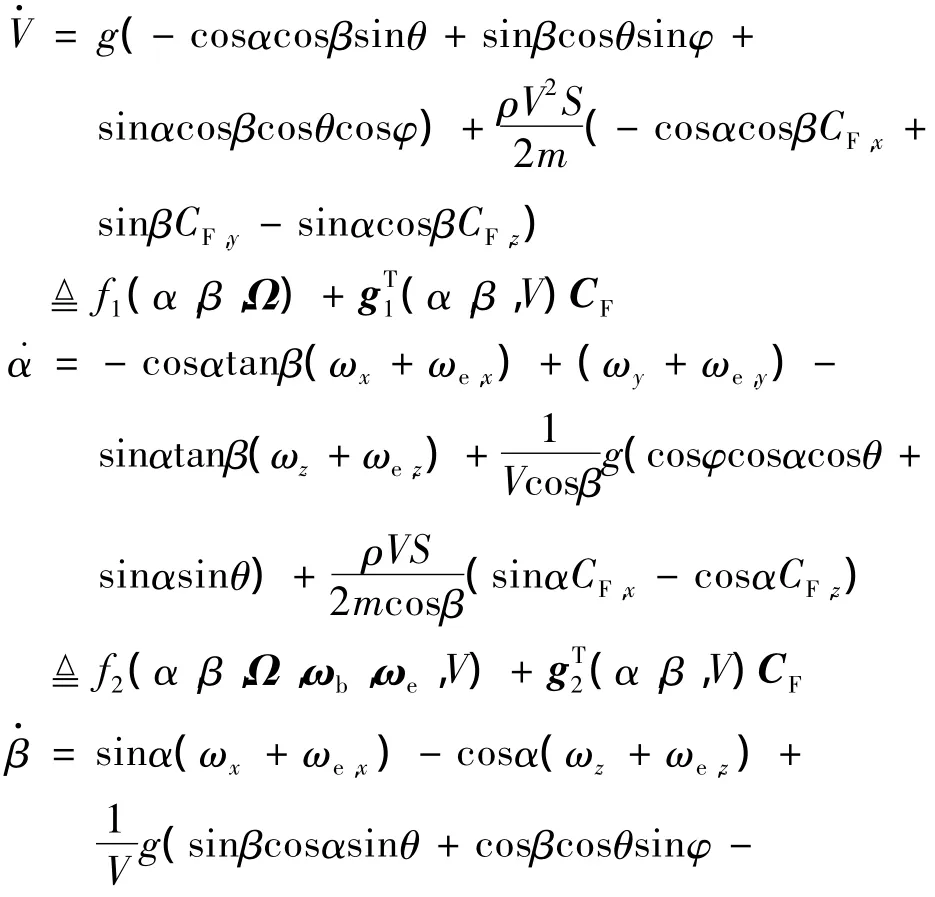
用速度V，攻角α和侧滑角β表示的本体系下速度分量的运动学方程为

1.2 姿态动力学模型

在本体系下，飞行器姿态动力学方程可写为

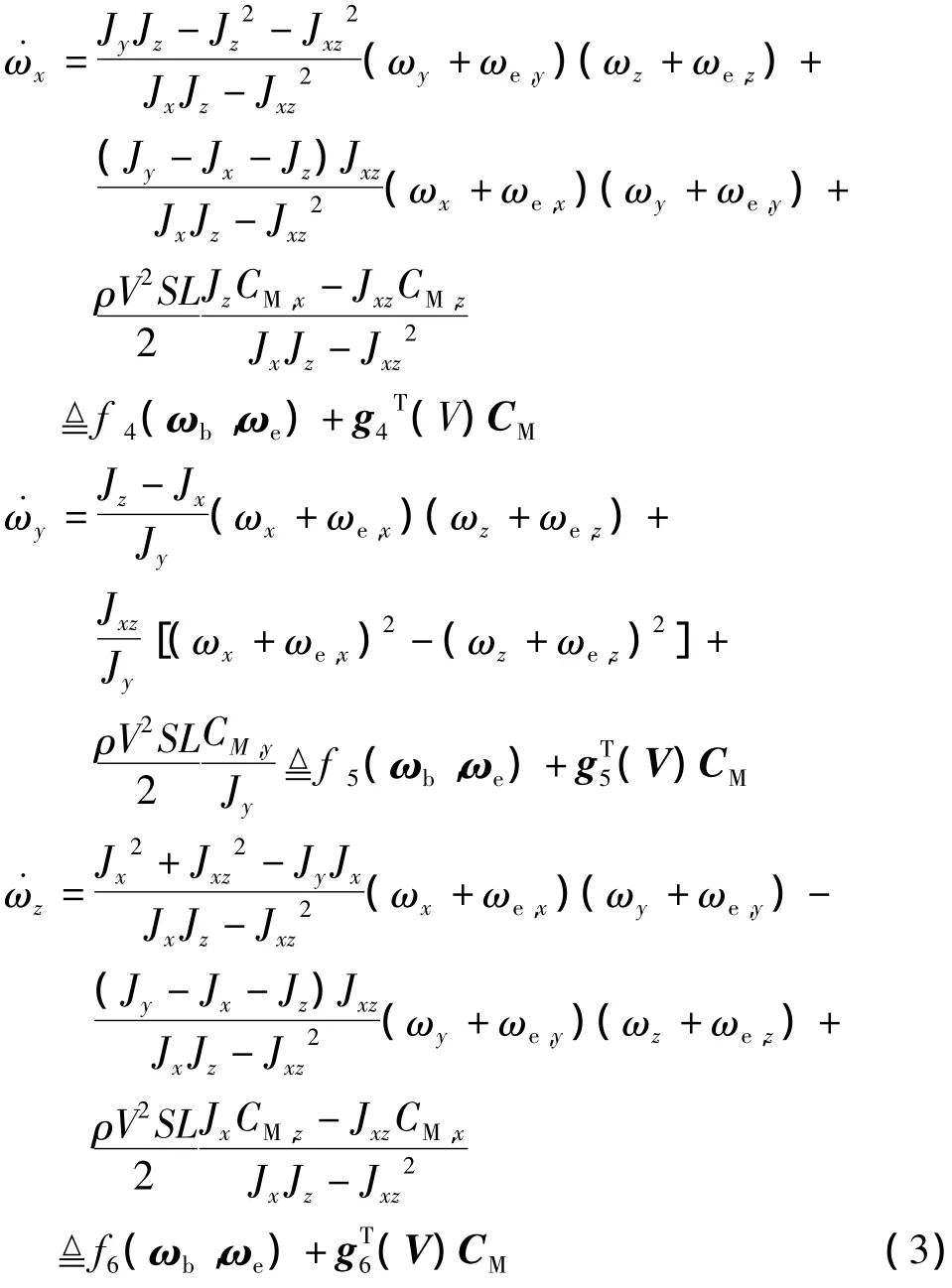
本体系下姿态角与角速度关系可表示为

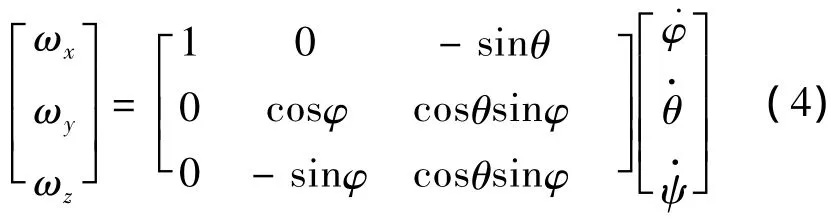
2 特征模型推导

观察在本体系下的质心动力学方程和姿态动力学方程，可以看到，以V，α，β，ωx，ωy，ωz作为状态变量，在假设ωe较小的条件下，整个系统可以看作由两个时间尺度不同的动力学子系统组成:慢子系统V，α，β和快子系统ωx，ωy，ωz(或，)，前者反映飞行器的轨迹运动，而后者反映飞行器的姿态运动，两个子系统形成级联形式.考虑到舵偏对气动力的影响很小，相比而言对气动力矩的影响却很大.因此，基于这种突出特性，对于慢子系统来说，它的实际控制输入应当是快子系统的输出(ωx，ωy，ωz)，对于快子系统来说输入为舵偏角.因此，以α，β，φ作为输出，在侧滑角较小的假设下，对系统进行简化可以得到以下主要关系:

1)α←ωy←My:α的变化主要由ωy决定，ωy的变化主要由外部输入My决定，而影响My的舵偏是升降舵;

2)β ← ωx，ωz←-Mx，Mz:β 的变化在 α 较小时主要由 ωz决定，而 ωz的变化主要由-Mx，Mz决定，同样，在α较大时，主要由ωx决定，但最终还是取决于-Mx，Mz，-Mx，Mz又主要取决于方向舵和副翼;

3)φ←ωx←Mx，-Mz:φ的变化主要由ωx决定，ωx的变化主要取决于Mx，-Mz，即主要由方向舵和副翼控制.

从以上主要耦合关系可见，攻角通道相对独立，滚转角和侧滑角通道在输入上互相耦合.下面根据上述的主要关系基于原动力学方程构建特征模型.

2.1 攻角通道

对式(1)中的求导，得

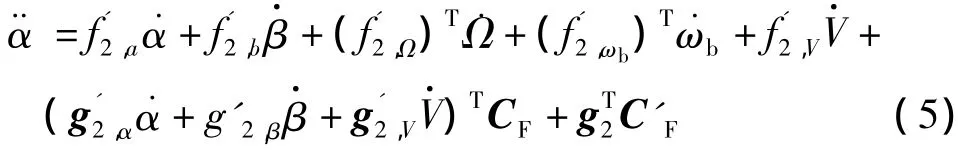
由于气动力或气动力矩系数都是攻角、侧滑角、高度和马赫数及舵偏的非线性函数，很难获得其解析表达式，下面为了处理方便，对气动力或气动力矩系数泰勒展开可得

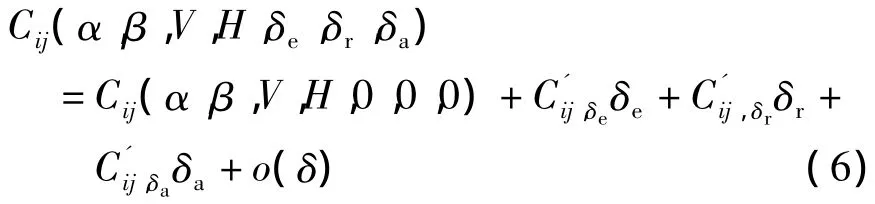
对其求导可得

把式(1)、(3)、(6)和(7)代入(5)可得

其中，

对其离散化并写成特征模型的形式有

其中，

其中，h为采样周期，常数0＜ε≤1.

2.2 侧滑角通道

把式(1)、(3)、(6)和(7)代入(9)得

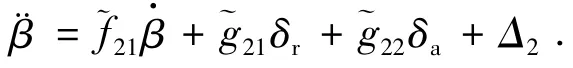
其中，

勃列日涅夫为重新斯大林主义化，主要通过一些行政措施对站在反斯大林主义立场上的人施加压力，但又不采取或很少采取极端的手段，如逮捕判刑等。“一般的做法是革职，给予严厉的党纪处分，直至开除党籍，以及用越来越巧妙的手段搞臭和迫害持不同政见者，包括公开诋毁中伤他们，送入精神病医院，乃至驱逐出境，剥夺苏联国籍等等。”[33]191

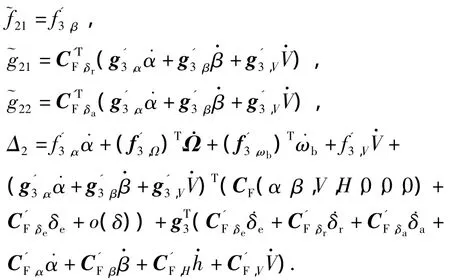
对其离散化并写成特征模型的形式有

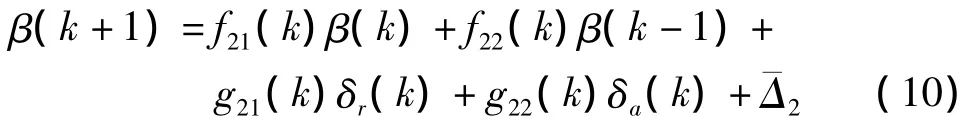
其中，

2.3 滚转角通道

仿照上面步骤，进行如下处理.对式(4)中

进一步求导，得

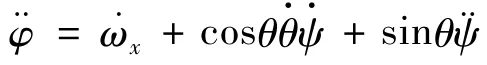
把式(3)中的表达式代入可得

其中，

对其离散化并写成特征模型的形式有

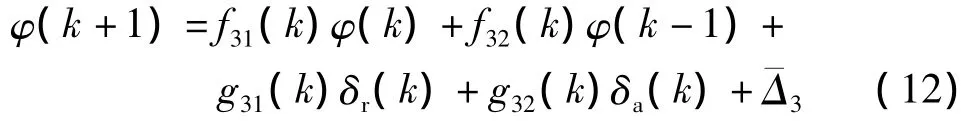
其中，

综合式(8)、(10)和(12)，高超声飞行器动力学模型以升降舵、副翼、方向舵为输入，以攻角、滚转角和侧滑角为输出的三输入三输出系统可以用如下二阶时变差分方程组来等效表示系统输入输出关系.

其中，fi，j，gi，j，i，j=1，2，3 为时变系数.

3 控制器设计

针对上面特征模型，可把攻角通道看作单输入单输出系统，其他两个通道看作是双输入和双输出系统，采用分散控制.利用文献［17］中提出的黄金分割自适应控制器和维持跟踪、逻辑微分、逻辑积分控制器，由于以上控制器除双输入双输出通道的黄金分割和维持跟踪控制器考虑耦合与文献［17］不同外，其他均完全一致.因此，此处只列出滚转角和侧滑角通道的黄金分割和维持跟踪控制器的具体形式.系统为一双输入双输出系统，可利用求逆解耦，设计控制器如下.

3.1 滚转角、侧滑角通道控制器设计

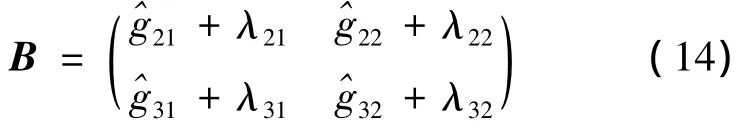
设，j(k)为参数估计值;λi，j为设置参数，i，j=1，2，3

1)黄金分割控制器

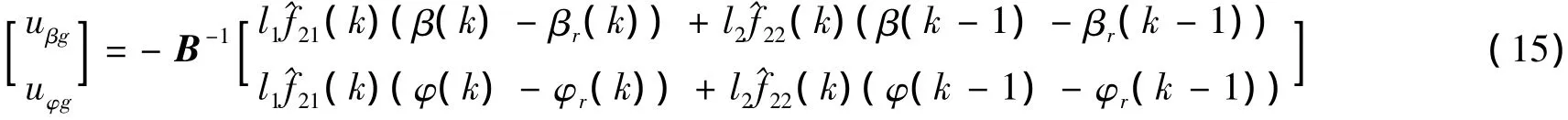
其中l1=0.382，l2=0.618 ，βr，φr为参考轨迹.

2)维持跟踪控制器

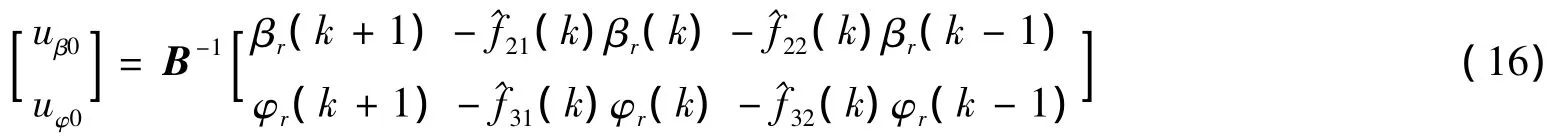
3.2 参数辨识

系统辨识算法采用梯度法，以特征模型(13)作为辨识的参数化模型，根据文献［17］中“全系数自适应控制理论”的系数特性选择辨识初值.

4 仿真验证

为验证该控制器性能，对此类X-20飞行器，给定初始条件为飞行器从60km高空，以6000m/s初始速度开始飞行.为了验证其鲁棒性，在存在以下不确定性因素下，进行仿真.

a)气动力矩系数偏差:±30%(在气动力矩处叠加一慢变的振幅为气动力矩3/10的正弦信号模拟气动力矩系数偏差);

b)转动惯量偏差:±10%(在转动惯量处叠加一慢变的振幅为转动惯量1/10的正弦信号模拟转动惯量偏差);

c)大气密度偏差:45km高度以下取±10%，70km高度以上取±25%，45～70km高度按线性插值;

d)考虑风速的影响:风向取水平侧风，风速随高度插值计算，数据数表如表1所示.

表1 风速数据表

设定具体仿真如下:

1)为验证跟踪能力，令滚转角跟踪一幅值为180°，周期为30s的方波信号，攻角保持15°，侧滑角保持0°.分别对没有上述扰动和存在扰动的情况下进行仿真，如图1所示.

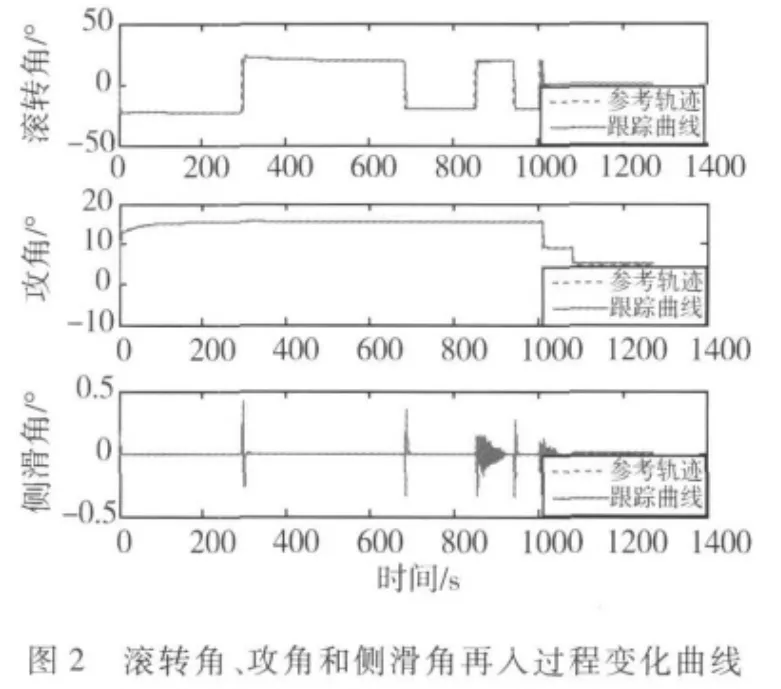
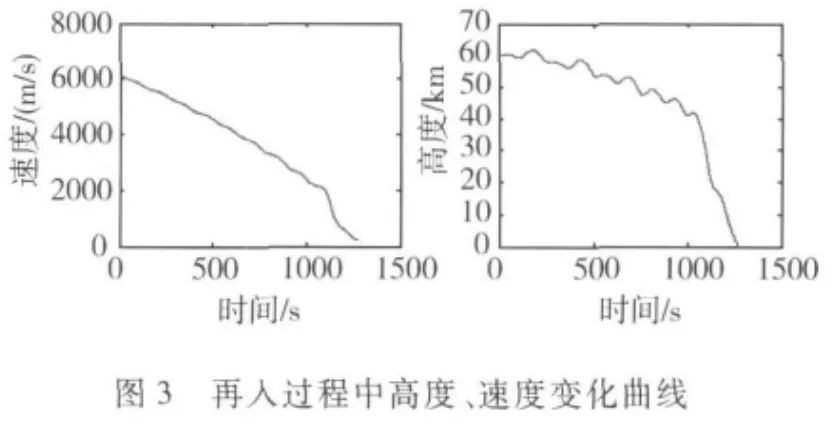
2)为验证整个再入过程中对制导律的跟踪能力和对大扰动、飞行环境大范围变化的鲁棒性，跟踪一个再入制导轨迹，滚转角来回翻转实现横向航程的控制，利用攻角变化实现纵向航程的控制，侧滑角保持0°，如图2所示，并在图3中给出整个飞行过程的高度和速度变化曲线.

5 结论

采用特征建模的思想，就是在原来复杂的动力学模型的基础上抓住系统输入输出的主要关系，得到考虑控制要求的更为简洁的特征模型，使得控制器设计简化.从最后的仿真结果可以看到，根据系统的耦合关系，采用分散控制策略构建特征模型，并基于此得到的黄金分割自适应控制器在飞行器再入过程中，在大扰动、大范围变化的气动参数的情况下可以较好地完成姿态跟踪，并能够在长距离的、环境剧烈变化的飞行条件下实现再入.充分证明了这种方法处理复杂控制问题的有效性.

［1］ 朱云骥，史忠科.高超声速飞行器飞行特性和控制若干问题［J］.飞行力学，2005，23(3):5-8

［2］ 刘子强，崔尔杰，傅光明，等.高超声速飞行器的空气弹性问题［C］.中国第一届近代空气动力学与气动热力学会议，绵阳，2006

［3］ Fidan B，Mirmirani M，Ioannou P A.Flight dynamics and control of air-breathing hypersonic vehicles:review and new directions［C］.The 12thAIAA International Space Planes and Hypersonic Systems and Technologies，Norfolk，Virgina ，December 2003

［4］ 许赞，谢长川，杨超.高超声速飞行器若干气动弹性问题［C］.第十届全国空气弹性学术交流会，日照，2007

［5］ 孙未蒙，张靖男，郑志强.高超声速飞行器控制技术的几个增长点［C］.中国航空学会控制与应用第十二届学术年会，西安，2006

［6］ DARPA explains falcon HTV-2 flight failure［Z］.http://www. flightglobal.com/articles/2010/11/9/350005/darpa-explains-falcon-htv-2-flight-failure.November 19，2010

［7］ Gregory I M，Chowdhry R S，McMinn J D，et al.Hypersonic vehicle model and control law development using H∞and μ synthesis［R］.NASA TM-4562，1994

［8］ Smith R，Ahmed A.Robust parametrically varying attitude controller designs for X-33 Vehicle［C］.AIAA Guidance，Navigation，and Control Conference and Exhibit，Denver，CO，August 2000

［9］ Xu H J，Mirmirani M D，Loannou P A.Adaptive sliding mode control design for a hypersonic flight vehicle［J］.Journal of Guidance，Control，and Dynamics，2004，27(5):829-838

［10］ Georgie J，Valasek J.Selection of longitudinal desired dynamics for dynamic inversion controlled re-entry vehicles［C］.AIAA Guidance，Navigation ，and Control Conference and Exhibit，Canada，2001

［11］ Matthew D J，Anthony J C，Eric N J.Evaluation of an adaptive method for launch vehicle flight control［C］.AIAA Guidance，Navigation，and Control Conference and Exhibit，Austin，Texas，August 2000

［12］ Xu H J，Mirmirani M，Ioannou P A.Robust neural adaptive control of a hypersonic aircraft［C］.AIAA Guidance，Navigation，and Control Conference and Exhibit，Austin，Texas，August 2003

［13］ Johnson E N，Calise A J，El-Shirbiny H A.Feedback linearization with neural network augmentation applied to X-33 attitude control［C］.AIAA Guidance，Navigation，and Control Conference and Exhibit，Denver，CO，August 2000

［14］ 李菁菁，任章，宋勋，等.临近空间高超声速飞行器鲁棒自适应控制方法［J］.上海航天，2010，27(5):1-6

［15］ 黄显林，葛东明.吸气式高超声速飞行器纵向机动飞行的鲁棒线性变参数控制［J］.宇航学报，2010，31(7):1789-1797

［16］ 周丽，姜长生，钱承山.一种基于神经网络的快速回馈递推自适应控制［J］.宇航学报，2008，29(6):1888-1898

［17］ 吴宏鑫，胡军，解永春.基于特征模型的智能自适应控制［M］.北京:中国科学技术出版社，2009