一种在轨改善偏置动量卫星控制精度的方法
2011-04-17魏春岭
柯 旗,王 勇,魏春岭
(1.北京控制工程研究所,北京 100190;2.空间智能控制技术重点实验室,北京 100190)
偏置动量卫星作为一种配置简单、可靠长寿的卫星在低轨道遥感卫星、高轨道通讯卫星上得到广泛应用.一般偏置动量卫星都采用对地定向三轴稳定的控制方式,在卫星的-Y轴(即轨道法线方向)装有一个偏置在固定角动量的动量轮.由于偏置动量卫星的定向性所产生的陀螺罗盘效应,使得卫星的偏航误差将随卫星在轨道上的运动耦合为滚动误差,这样控制系统只用控制滚动角和俯仰角就可维持卫星的对地姿态,因此只需一个红外地球敏感器就可以提供控制系统所需的测量信息.在正常对地定向运行过程中,偏置动量卫星控制回路的构成是:采用红外地球敏感器的测量信息进行姿态确定,俯仰轴采用PID轮控方式,滚动和偏航轴采用磁控.这种卫星的姿态控制精度一般约在0.5°以内.
1 问题的提出
偏置动量卫星技术成熟,控制简便.然而卫星在轨飞行期间常常可以发现:遥测参数显示中的滚动角偏在坐标轴一侧,峰峰值可能不大,但最大(最小)值可能超出1°,这远远超出了偏置动量卫星的控制精度指标,如图1所示.
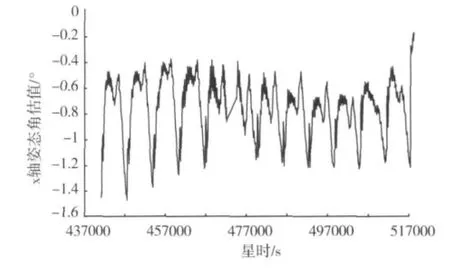
图1 某卫星一天滚动角估值的遥测曲线
从图1可以看出,滚动角有一个常值偏差,从偏置动量卫星的控制系统构成上,可以推断出这个偏差的来源主要有两个:1)红外地球敏感器的系统误差;2)偏置动量轮的安装误差.
下面就这两个误差源进行具体分析.
2 误差源的分析
2.1 红外地球敏感器系统误差的影响
红外地球敏感器数据处理中除了随机误差外,还包括安装误差、标定误差、算法模型误差等多重误差,我们暂且将这些误差项都叫做系统误差,归为常值误差类.用数学仿真模拟当红外有系统偏差和没有系统偏差的情况,姿态对比曲线见图2~3.
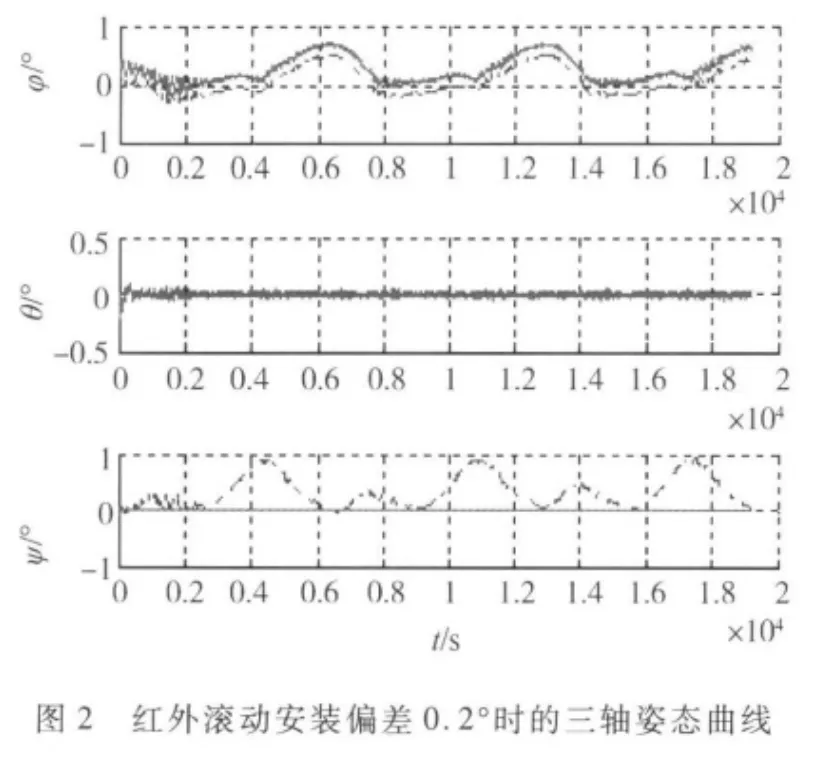

图3 红外无系统偏差的三轴姿态曲线
从图2和图3可以看出,红外地球敏感器有无系统误差前后,姿态角的幅值变化不大,但红外地球敏感器在有系统误差的情况下,滚动轴明显向坐标轴一侧偏移了.
卫星上的磁力矩器产生磁矩矢量,和当地地磁场作用生成磁控力矩的表达式如下:

式中,T是磁控力矩,M是磁力矩器输出的磁矩矢量,B是地磁场强度矢量.
当卫星正常对地定向工作时,Y轴磁力矩器采用的磁控规律为

式中,My是Y轴磁力矩器输出磁矩,Bx,Bz是地磁场强度在本体系下X轴和Z轴的分量,和是卫星滚动角和滚动角速度的估计值.
由式(1)和(2)可以得出X轴输出的磁控力矩为

式中,Tx是X轴的磁控力矩.可以看出,红外地球敏感器的系统误差的影响主要在式(3)的右侧第一项上,如果令

式中,Δφ为系统误差,则

由于Δφ是一个常值,当Δφ和符号相同时,Tx力矩比实际需要力矩要大;而当Δφ和符号相反时,Tx力矩比实际需要力矩要小,特别是Δφ和幅值相仿时,滚动角就表现为被推向坐标轴的一侧.另外,由于BxBz是一个周期变化量,变化频率为2ω0(ω0为轨道角速度),所以KpBxBzΔφ 项在一个轨道周期内的积分的角动量接近于0,因此长期看,红外地球敏感器的系统误差产生的磁控力矩对卫星实际角动量影响不大,也就表现为滚动角虽然偏置在坐标轴的一侧,但幅值大小变化不大.
2.2 动量轮的安装偏差的影响

由于偏置动量卫星在卫星-Y轴方向有一个常值角动量,此角动量是由动量轮提供的,卫星的动力学方程为如果动量轮的转轴和星体Y轴平行时h=[0,hy,0]T,则当动量轮有安装误差时(假设动量轮转轴绕星体X轴旋转了α角,绕Z轴旋转了β角,当α和 β 较小时)h'=[hyβ,hy,-hyα]T,带来的干扰力矩约为 TH=[-hyαω0,0,-hyβω0]T(ω0为轨道角速度).动量轮安装偏差对姿态的扰动见图4~5.
从图4和图5可以看出,动量轮的安装偏差同样可以导致滚动角偏移坐标轴的情况发生,同时滚动角和偏航角的幅值还有所增长.这明显是动量轮安装偏差产生一个的常值干扰力矩的影响所至.

图4 动量轮安装偏差对姿态的影响(α=0.3°,β=0.3°)

图5 动量轮无安装偏差的三轴姿态曲线
从这一现象引出了一个卫星本体坐标系定义的问题:一般卫星是先定义一个本体坐标系,然后在安装各测量敏感器和执行机构时向这个本体坐标系看齐,测量和控制也都是施加在这个本体系上的.但由于偏置动量卫星的特殊性,其偏置动量方向和轨道面法线一致时,星体的姿态最佳.但当动量轮的安装不平行于星体的Y轴,而测量和磁控的实施还是基于本体坐标系时,轮子的干扰力矩就会对姿态产生不良影响.
3 修正方法
综合上述分析,可以认为滚动姿态的常值偏差既可能由红外系统偏差造成,也可能由于动量轮安装偏差引起的,或是两者合力所致.但红外系统误差的影响只会导致姿态偏向坐标轴的一侧,对姿态的幅值没有影响;而动量轮的安装偏差对姿态的偏移和幅值都有影响.
对上述问题的解决办法是:1)红外系统误差的影响可以方便地采用增加红外误差修正项(一般简称为红外安装偏差)来加以改正.2)动量轮的安装偏差虽然问题出在动量轮身上,但从系统的角度考虑,令卫星的偏置角动量方向指向轨道法线控制效果最佳,可以通过重新设定本体坐标系来改善动量轮安装偏差带来的负面影响,即设定动量轮的输出轴方向为卫星的-Y轴.这样,对于以原来本体坐标系为基准的测量敏感器来说,与新坐标系的偏差可以归结为一种安装偏差.因此,动量轮的安装偏差也可以通过调整红外地球敏感器的安装偏差来修正.综上所述,对于偏置动量卫星滚动姿态偏移的问题,都可以通过修改红外滚动的安装误差来实现.这种方法经过在轨测试,是可行的,而且效果明显.
下面给出了两颗在轨卫星调整红外安装误差前后的姿态曲线图.
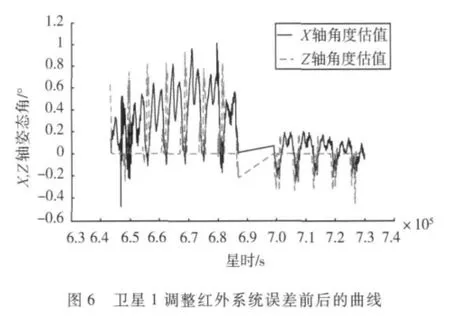
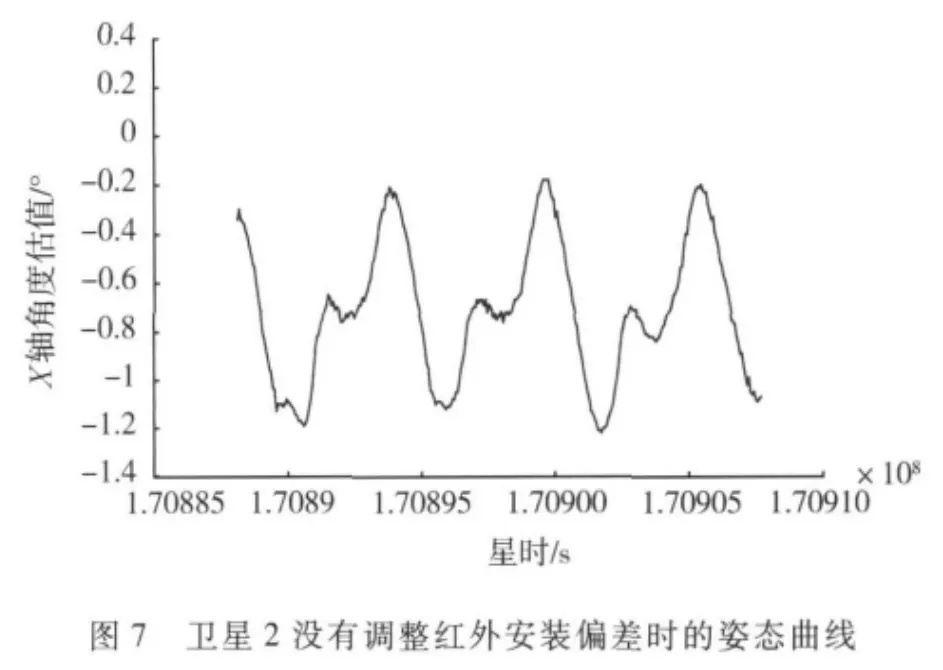
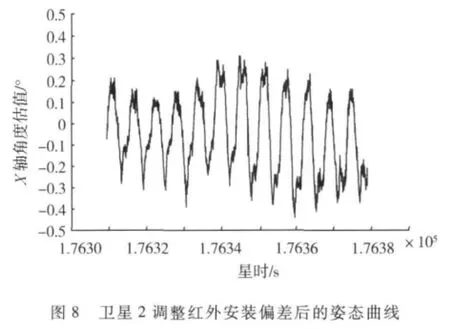
从图6中可以看出,修改了红外安装偏差后,滚动姿态的偏移得到纠正且幅值也减小,说明其中有动量轮的安装偏差的因素;而图7和图8中,经过修正,只是姿态的偏移减小了,而姿态幅值没有发生变化,因此这个误差因素主要来自红外的系统偏差.
4 结论
综上所述,偏置动量卫星发生滚动角偏向坐标轴的一侧的问题,原因在于红外地球敏感器的系统偏差和动量轮的安装偏差.其中,红外的系统偏差会影响姿态的偏移,而对幅值影响不大;但动量轮的安装偏差对二者都有影响.
对这种姿态偏移的修正方法就是在红外的数据处理中增加安装误差修正项.从卫星的在轨应用中可以看出上述方法是行之有效的,可以明显地改善姿态控制精度,并有很好的推广价值.
[1] 章仁为.卫星轨道姿态动力学与控制[M].北京:北京航空航天大学出版社,2006
[2] 屠善澄.卫星姿态动力学与控制[M].北京:宇航出版社,2002
