一种组合体航天器帆板的光照遮挡计算新方法
2013-09-19黄岸毅李俊峰
黄岸毅,宝 音,李俊峰
(1.中国西安卫星测控中心宇航动力学国家重点实验室,西安710043;2.清华大学航天航空学院,北京100084)
1 引言
在航天器电源系统设计中能量平衡分析和计算是一项重要的工作,即通过负载、帆板发电情况计算得到电池组的工作状态,判断其是否满足设计需要。每一时刻的帆板发电信息,主要取决于太阳光与帆板法线的角度、帆板发电效率、光照强度、遮挡面积等。受遮挡的帆板不发电,组合体航天器的遮挡关系复杂,所以计算太阳帆板的遮挡面积对组合体航天器非常重要。
通常航天器会在帆板和舱体的连接处设置支架,使其间距增大,可以较大程度避开遮挡的高发区。在航天器的交会对接飞行试验中,追踪飞行器和目标飞行器通过对接机构完成物理连接后,形成组合体并进行联合飞行。组合体外形尺寸进一步增大,太阳帆板数目增多,组合体本体对太阳帆板的遮挡更为严重,同时还存在帆板对帆板的遮挡。目前国内外相关研究较少,文献[1]提出了一种简化圆柱形舱体模型,通过直接计算其轮廓在帆板上的投影确定遮挡范围,计算量较小但对舱体的简化较多。由于光压面积分析与遮挡分析有一定的相似性,可借鉴其中离散化与有限元的思想[2-3]。
本文提出一种计算组合体光照遮挡的新方法,根据舱体轴线与帆板转轴垂直的几何关系,将舱体沿轴线离散化为若干平面,将待分析帆板离散化为点,以判断离散点沿太阳矢量逆向是否经过离散的舱体平面或其它帆板平面来判断是否遮挡。对于轴对称航天器由于离散平面均为圆形,计算过程简捷、适于计算机实现。
2 航天器模型建立
图1为典型轴向对接航天器模型的平面视图,第三节将针对此类航天器设计遮挡计算方法。

图1 组合体模型Fig.1 Combination model
2.1 基本假设
基于本文的研究背景,其遮挡分析模型可进行如下假设:太阳光为平行光,不考虑光线的透射和反射,航天器为轴对称体,多个组合体对接后也仍保持整体的轴对称性。
设定太阳帆板的转轴与本体对称轴垂直,帆板可绕转轴360°旋转,同时转轴可随本体轴向旋转。
2.2 坐标系定义
轨道坐标系(O0-X0Y0Z0):Z轴指向地心,X轴在运动平面内与Z轴垂直,指向前进方向,原点为航天器质心,Y轴为轨道平面法线方向,与Z轴、X轴构成右手系。
本体坐标系(Ob-XbYbZb):定义航天器轴向为X轴,帆板转轴为Y轴,这里为方便计算取原点位于航天器轴向的某一侧(见图1,取底部中心为原点),Z轴可由右手坐标系特性得出。对组合体取其中某一本体坐标系作为组合体的本体坐标系即可。
帆板坐标系(Ov-XvYvZv,对每个帆板单独定义):定义帆板转轴由舱体向外部方向为帆板坐标系的Y,帆板平面的负法向为Z轴,X轴与YZ构成右手系。显然若不考虑厚度则帆板位于XY平面内。
2.3 模型主要参数
建立模型需要下述信息(图1):
舱体设为一系列同轴圆(控制截面)拉伸和连接的结构,对应图中舱体部分的横线,需要给定每个控制面X方向的位置和圆的直径。
帆板参数:每一块帆板的转角(帆板在本体坐标系XY平面内时为0,沿其帆板坐标系+Y方向逆时针转动为正);帆板的长度和宽度(通常一块帆板可再细分为沿Y轴以一定间隔并列分布的若干块,此时需给出详细的长宽及间隔大小);帆板坐标系原点在本体坐标系的三维坐标(用于定位帆板)。
在实际应用中,每块帆板由数千个电池片单元组成,故需要的参数为每一个单元中心在帆板平面坐标系中的位置及其单元面积。这些单元的集合即可看作离散化后的帆板。
3 遮挡计算算法
航天器本体坐标系下的太阳矢量可由航天器轨道根数和姿态信息(主要为偏航,侧摆等)以及太阳相对地球的位置计算得到[4],这里给出太阳矢量为S=[S1S2S3]T。
帆板转轴默认设置为平行于本体系的Y轴,若其本身也存在绕X轴的旋转,即转轴方向发生变化,在分析时可认为太阳矢量绕X轴向相反方向转动了相同的角度,这样得到一个等效的太阳矢量X',帆板转轴仍按照不转动来处理,得到的结果是相同的。
对组合体而言,遮挡可以分为两类:舱体对帆板和帆板对帆板的遮挡。把这两类结果求并集就是帆板受到的全部遮挡。
3.1 舱体对帆板的遮挡
首先将舱体离散化为平面集。根据给定的控制面,按照合适的间隔用相邻的两个控制面插值得到均匀分布的离散圆形平面(数据包括该圆平面的X坐标,直径d),如图2。

图2 模型离散示意图Fig.2 Schematic diagram of discredited model
对于每个帆板单元中心点在帆板坐标系的坐标(x,y),将其变换到本体坐标系中的(X,Y,Z)。

其中Apb为帆板坐标系到本体系的转换矩阵。(X0,Y0,Z0)为每块帆板坐标系原点对应的本体系坐标。
将每个帆板离散单元沿着太阳矢量方向投影到组合体本体的各个圆形截面上,设投影点在某一离散平面上的坐标为X'、Y'、Z'在本体坐标系中有二者的连线与太阳矢量平行:

因投影点在离散平面上,所以有:X'即该圆形截面数据中的已知量,则根据(2)式可求得k,X',Y'的值。
设圆截面的直径为d,则投影点到组合体离散面圆心的距离为:

与圆的直径d比较,若r<d/2则投影点在圆内,显然此时该平面遮挡住了帆板单元(图3)。
若r>d/2则投影点在圆外,即帆板单元未受到遮挡。如图4所示。
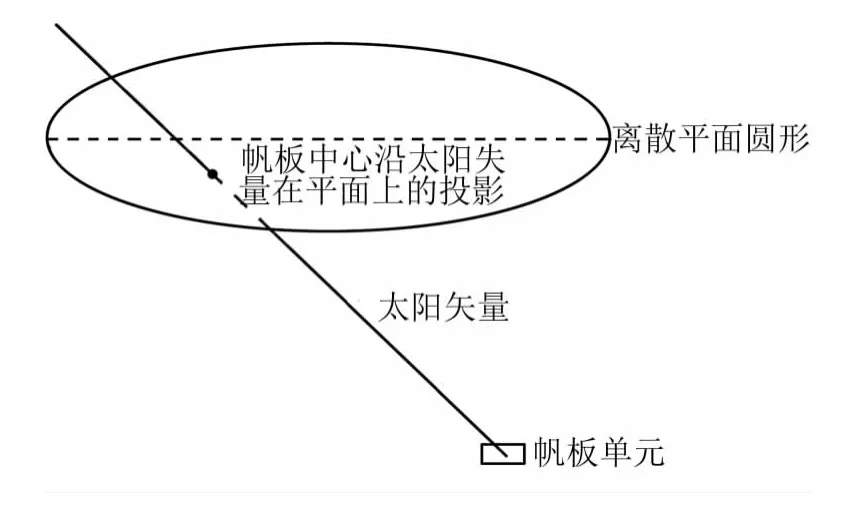
图3 帆板单元受到遮挡示意Fig.3 Panel unit in body shadow

图4 帆板单元未受遮挡示意Fig.4 Panel unit out of shadow of body
对一个帆板单元遍历判断所有的离散平面,若有一个遮挡就表示其受到航天器本体的遮挡,若所有的平面都未遮挡则认为未受到航天器舱体的遮挡。
3.2 帆板之间的相互遮挡
遮挡帆板可看作是一个平面矩形,判断其是否遮挡住另一帆板的某个单元,与3.1节类似。只需求出平面上该单元沿太阳矢量逆向的投影点,投影点在矩形范围内即为遮挡。
单元坐标(X,Y,Z)与2.1相同,不同点在于帆板平面与可以绕其转轴转动,投影点坐标(X',Y',Z')的X'不是已知量,需要补充方程,这里按照式(2)求解得到式(4):
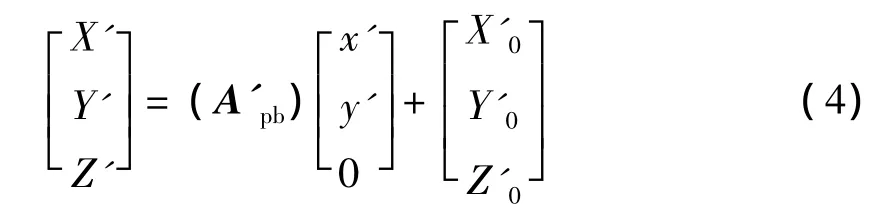
式(4)表示投影点在遮挡帆板平面上,一定是该帆板平面坐标系下某一点(Z坐标为0)经过坐标变换得到的,A'pb为遮挡帆板的帆板系到本体系的转移矩阵,(X0,Y0,Z0)为帆板坐标系原点对应的组合体本体系坐标。
解得(X',Y',Z')和(x',y')后,只需判断遮挡帆板坐标系下(x',y')的大小。例如给定的帆板坐标系下的其大小约束为下式表示的矩形:-1.5<x'<1.5,1<y'<8,则满足这个式子表明要分析的单元被遮挡帆板遮挡住,不满足则表明未遮挡住。
上述几何关系见图5。

图5 帆板单元受到其它帆板遮挡Fig.5 Panel unit in shadow of other panel
4 仿真结果
4.1 参数设置
设航天器舱体控制面如表1所示。

表1 舱体控制面参数(mm)Table 1 Parameters of body sections(mm)
两组对称帆板大小分别为:6.4 m×3 m,6 m×2 m。位置参数如下:
转轴处本体X坐标分别为1.8 m,16.0 m;帆板与本体X轴的最近处距离分别为2.8 m,2.5 m。
4.2 不同太阳光入射方向和帆板转角的遮挡分析结果
根据给定参数绘制遮挡图形如下,黑色为受到遮挡的单元。
1)当太阳矢量为(1,0,0),帆板转角均为 -90°时:此时帆板都正对太阳光,无舱体遮挡(图6-1)。
2)太阳矢量为(cos20°,- sin20°,0),帆板转角均为 -90°:由于太阳光矢量与X轴有20°的夹角,但还在XY平面内,所以存在舱体对右侧帆板的遮挡(图6-2)。
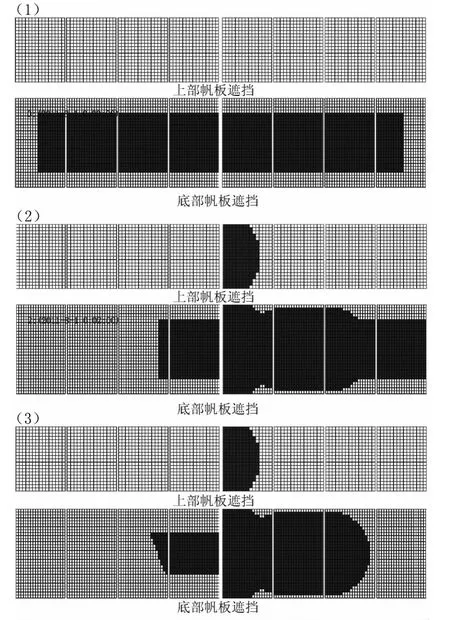
图6 遮挡结果Fig.6 Shadow result
3)太阳矢量为(cos20°,- sin20°,0),上部左右帆板转角分别改为 -45°和 -10°:舱体遮挡不变,帆板遮挡由于上部帆板的转动(相当于侧身)而变小,同时上部帆板也受到了很小的舱体遮挡(图6-3)。
4.3 结合实际航天器轨道和太阳位置计算得到的一个周期遮挡率变化
遮挡率即帆板受遮挡面积/总面积,以某300 km高度近圆轨道为例,由精密轨道动力学模型[5]计算一个周期左右,结果如图7所示。这里假定航天器姿态为三轴稳定Z轴对地指向,帆板自动转动确保其始终面向太阳。
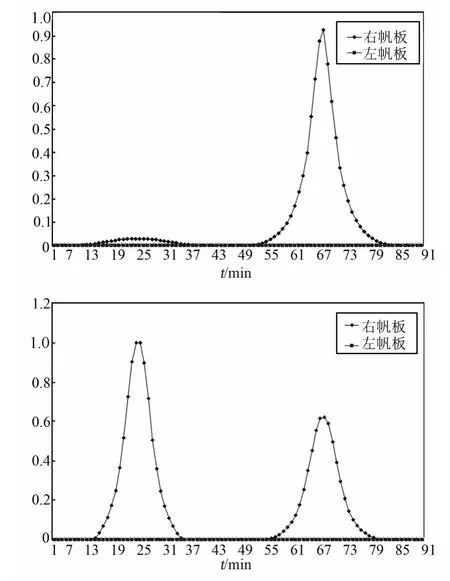
图7 遮挡率变化Fig.7 Change of shadow rate
从图中可见,一个轨道周期内帆板所受遮挡存在一个峰值,两对帆板的时间正好错开,这是由于太阳光沿着本体X正向照射时,上部的帆板几乎不受舱体影响,底部的帆板受舱体影响很大且可能受到别的帆板的遮挡。反之则底部的帆板受影响较小。除峰值处其它大部分时间由于太阳光与XY平面夹角较大(斜射时本体投影绝大部分不在帆板范围内),所以基本无遮挡。
5 结论
本文基于几何学方法建立了轴对称组合航天器的太阳帆板遮挡模型,能够对不同姿态和帆板转动状态下的帆板遮挡情况进行快速分析,可自动适应不同的模型参数。与圆柱体遮挡计算[1]相比更精确,且可以很容易的将其推广到非轴对称体,只需得到相应的离散平面集合即可进行分析。仿真结果表明,所建模型能够精确地分析各太阳帆板遮挡面积和遮挡区域,可根据分析结果由电路信息计算太阳能电池组的发电功率并进一步根据负载进行能量平衡分析。本方法已经在实际航天任务电源系统分析中得到应用。
[1] 黄海兵,唐国金,李海阳.组合体太阳帆板遮挡分析[J].系统仿真学报,2009,21(11):3215-3218.
[2] 刘暾,赵志萍.卫星太阳光压力矩计算中有效作用面积的计算[J].南京理工大学学报,2007,6(31):684-688.
[3] Marek Ziebart.Generalized analytical solar radiation pressure modeling algorithm for spacecraft of complex shape[J],Journal of Spacecraft a Rockets,2004,41(5):840-848.
[4] 章仁为.卫星轨道姿态动力学与控制[M].北京:北京航空航天大学出版社,2001:39-70.
[5] Long AC,Cappellari JO,Velez CE,et al.Goddad Trajectony Determination System(GTDS)-Mathnatrcal Theory(Rev 1)[M].Goddard Space Flight Center,1989:20-110.
