基于RCMAC网络的动态逆再入制导方法研究

吴 浩，杨 业

(北京航天自动控制研究所，北京 100854)

升力式再入飞行器在长距离飞行过程中从稀薄大气进入稠密大气，受到气动偏差、大气密度偏差、风场干扰等因素的影响较大，而飞行过程中对机体所承受的多约束条件以及终端约束等条件有严格要求.因此，设计的制导方法需要具有良好的鲁棒性.传统的标准轨迹制导是通过控制升阻比(L/D)在纵向面内的投影来实现对标准升阻比的跟踪［1-2］.其控制结构从以往的PID控制［1，3］发展到动态逆控制［4］的方式.动态逆方法能够有效消除飞行器系统的非线性因素，在伪线性系统基础上通过相应的控制方法实现解耦和协调控制，但由于其对模型的依赖程度较高，在存在偏差或干扰较大的情况下，逆误差会使得控制效果恶化，引起制导精度降低.因此，神经网络［5］、滑模控制［6］等方法与动态逆相结合成为了当前飞行器制导控制的研究热点.

本文在基于动态逆的阻力加速度跟踪制导的基础上，引入自回归小脑模型神经网络(RCMAC)网络对模型的不确定项和外部干扰进行在线补偿，应用Lyapunov方法推导出RCMAC网络的权值更新规则，证明了闭环系统的稳定性.仿真结果验证了方法的有效性.

1 升力式再入飞行器运动模型

在再入飞行的过程中，假设地球模型为球形，飞行器为刚体，其受到的外作用力仅有升力、阻力和重力，忽略地球自转的影响，则描述飞行器运动的方程组可表示为［7］:

式中:r是飞行器地心径向距离，r=h+R0，h是飞行器当前高度，R0是球形地球模型的半径;θ和φ分别是飞行器当前的经度、纬度;v是当前的速度值;γ表示弹道倾角，是速度矢量与当地水平面间的夹角;ψ是航迹偏角;L和D分别是飞行器受到的升力加速度和阻力加速度，L=CLρv2Sm/(2m)，D=CDρv2Sm/(2m)，CL和CD是对应的气动升力和阻力系数;Sm是飞行器的有效面积;ρ是当前高度下对应的大气密度;α和σ分别是攻角和倾侧角，作为控制输入量.

2 标准轨迹的设计

对以阻力加速度-速度为投影坐标的飞行走廊而言，需要考虑过载、动压、驻点热流等多约束条件，其中最大的平衡滑翔能力对应最小阻力加速度，即走廊的下边界;最大驻点热流Qsmax、最大动压qmax、最大过载nmax构成了飞行走廊的上边界.

在忽略地球自转影响的条件下，剩余航程的表达式为

将式(2)与式(1)中的速度表达式相除，若满足准平衡滑翔条件，即弹道倾角γ≈0，可得

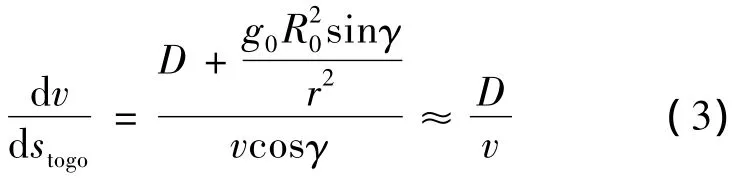
根据上式可以建立不同攻角和倾侧角模式下的速度和剩余航程间的映射关系，进而给出标准轨迹对应的阻力加速度和速度指令.

3 基于RCMAC网络的动态逆再入制导方法

3.1 基于阻力加速度的动态逆再入制导原理

大气密度与高度关系可用指数函数来描述:ρ=ρ0e-h/hs，则大气密度对时间求导有ρ.阻力加速度对时间求二阶导数，忽略D/CD项，有2.阻力加速度对时间的二阶导数为

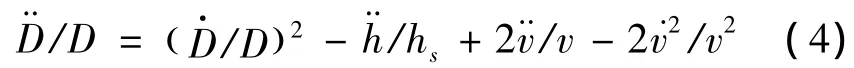
对和求导，对高度求两阶导数，有

将式(1)中的代入式(4)，并令u=Lcosσ/D，x=［rvγ］T整理得

其中，

引入伪线性控制量υ作为新输入，采用动态逆方法设计非线性控制器［8］，可得

使得与新输入υ量呈线性关系，有υ.

由于高速再入飞行过程中的气动参数变化、建模不精确以及外界干扰等不确定性因素的影响，将导致逆误差的产生，系统的实际动态特性可表示为:

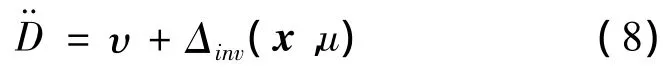
其中Δinv(x，u)为逆误差项.动态逆方法对于被控对象模型的精确程度要求很高，一旦出现系统干扰或误差项，控制效果会有一定程度的下降，因此本文引入RCMAC网络估计逆误差项，以提高动态逆方法对于不确定系统的鲁棒性.

3.2 RCMAC网络的结构

RCMAC网络是Lin等［9］在高斯基CMAC基础上提出的一种带有自回归单元的网络.其结构与广义高斯基CMAC网络类似，但是在联想单元的每个高斯基函数中引入了自回归单元，实现了网络的动态映射，在学习效率和动态响应速度有较大提高，适用于非线性系统的实时控制，其结构图如图1所示.

图1 RCMAC网络结构图

图中各区域分别是:

1)输入空间:对输入变量进行标准化处理，保证xi是连续有界的.

2)联想单元:对输入x1～xn进行量化.即将每个输入的区域划分为nB个块(Ai1，Ai2，…，AinB).输入xi对应的第j个块的接受域基函数为:

其中mij和σij分别是第i个输入的第j块的隶属度函数的中心值及宽度，xqi代表加入自回归单元后的输入，其表达式为:

qik＞0表示自回归增益系数，φik(t－T)代表延迟时间T的φik值.

3)接受域空间:将量化后的联想单元通过多维接受域函数形成空间中的元素.第k个多维接受域函数和相应的接受域空间定义为

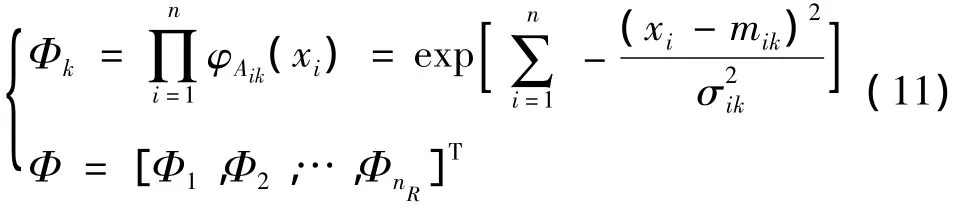
其中nR为结合后的接受域个数.

4)权值空间:W=［w1，…wi，…wnR］T，其中 wi=［wi1，wi2，…wim］.调整隶属度函数的中心值和宽度相当于调整步骤2)中的量化方式，从而调整多维接受域元素的位置和对输入状态的覆盖程度.

5)输出空间:将权值矩阵与接受域向量相乘得到系统输出，即 y=［y1，y2，…，ym］T=WTΦ.

3.3 基于RCMAC网络的动态逆再入制导

基于RCMAC网络的动态逆再入制导的结构图如图2所示.

图2 基于RCMAC网络的动态逆再入制导结构图

从图中可以看出，伪线性控制量υ由线性控制项υk、指令信号υcx、RCMAC网络输出υnn和鲁棒自适应项υr组成，即

其中线性控制项υk可设计为PD控制器，即υk=Kp(Dcx-D)+Kd()，Kp和Kd是线性控制器系数，υcx=cx.若定义e=Dcx-D，根据式(8)可整理得

假设1.根据神经网络的逼近原理可知，存在理想的RCMAC网络和相应的理想网络权值W*，理想的高斯基函数Φ*及函数中心值m*、宽度σ*和自回归系数q*，使得RCMAC网络一致逼近任意光滑非线性函数 Δinv(x，u)，即

取υnn=T，进一步展开式(13)，可得

假设2.若定义由可假设，即常数ψΔ为Δ的上界，误差上界估计误差，其中Δ表示对ψΔ的估计.

定理1.对于式(6)描述的非线性系统，采用如图2所示的再入制导结构，其中动态逆控制表达式为，伪线性控制项表达式为(7).在满足假设1和2的前提下，设计RCMAC输出υnn和鲁棒自适应项υr为

若将自适应调节规律选择为

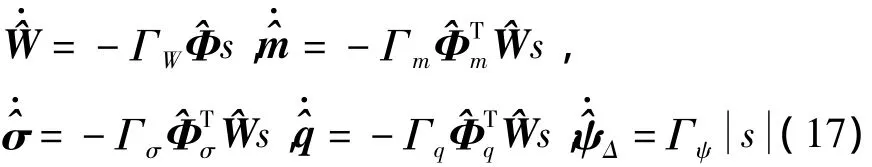
其中 ΓW，Γm，Γσ，Γq，Γψ＞0，则闭环系统所有信号最终有界.

证明.对s求导，代入式(15)可得

选择Lyapunov函数

对其求导可得

将式(15)和泰勒展开式代入可得

代入式(16)和(17)可得

由假设2的条件可知≤0，则闭环系统所有信号最终有界，定理得证.

由于式(16)中υr带有符号函数sgn(·)，即要求控制信号和执行机构瞬间转换，而在实际应用中这种转换容易引起抖振现象，因此将sgn(·)用饱和函数sat(·)代替，其表达式为

其中Λ＞0为设定的边界层厚度，可根据|s|的值适当选取，达到减弱系统抖振的目的.

4 仿真算例及结果分析

以X-20飞行器为例，飞行器初始状态［h0，θ0，φ0，v0，γ0，ψ0］=［62000m，0°，0°，6000m/s，0°，0°］，攻角固定为 15°.RCMAC 网络的输入为xNet=［Dcx－Dcx－］T，ni=2，no=1，每一维均分为 20级进行量化，初始权值均置为0，初始中心值mij平均分布，宽度σij由输入范围和量化等级确定，自回归增益q为 －0.1～0.1间的随机值.RCMAC的ΓW=0.2，Γm=0.05，Γσ=0.01，Γq=0.005，Γψ=0.01，边界层厚度Λ=1，PD控制器的增益系数取为Kp=0.005，Kd=0.08.

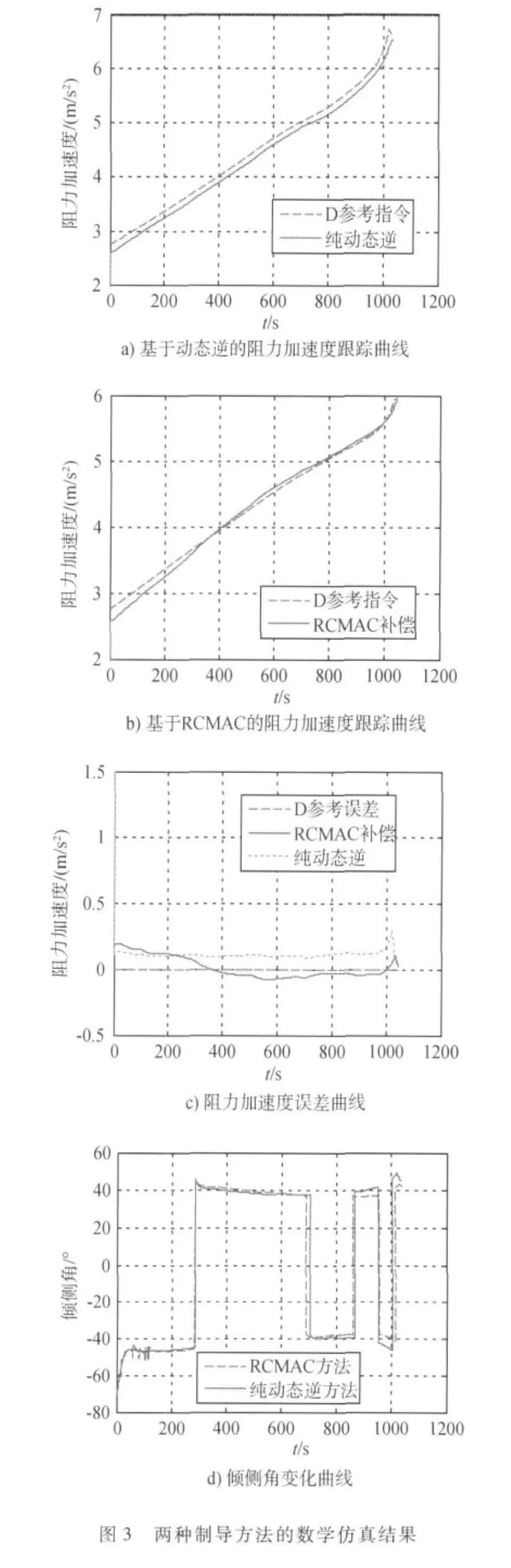
图3给出了升力系数偏差+15%采用动态逆方法和基于RCMAC网络的动态逆方法的三自由度仿真结果.其中a)和b)分别是基于两种方法的阻力加速度跟踪曲线，图c)是阻力加速度跟踪误差的比较.表1给出了基于RCMAC网络方法在气动偏差下的终端状态参数.

表1 气动偏差下的再入终端参数

通过仿真结果可看出，当升力系数偏离额定状态时，纯动态逆结果存在明显的跟踪误差，但引入RCMAC网络进对逆误差进行补偿之后，削弱了不确定因素的影响，误差明显减小，降低了非线性动态逆对精确模型的依赖.而表1中不同气动偏差下的终端高度、速度结果均能满足精度的要求，显示出该方法具有一定的鲁棒性.

5 结论

本文研究了升力式再入飞行器的制导方法.针对动态逆跟踪控制方法依赖于模型精确度的问题，提出了基于RCMAC网络的动态逆控制结构，利用RCMAC网络的非线性逼近能力和自学习能力和相应的控制结构，估计系统中存在的不确定项，实现了对规划出的阻力加速度指令的跟踪.X-20飞行器的三自由度仿真结果显示出该制导律的有效性.

［1］ 赵汉元.飞行器再入动力学和制导［M］.长沙:国防科技大学出版社，1997

［2］ Leavitt J A，Saraf A，Chen D T，et al.Performance of evolved acceleration guidance logic for entry(EAGLE)［C］.AIAA Guidance，Navigation and Control Conference and Exhibit，Monterey，California，2002

［3］ Hu J X，Chen K J，Zhao H Y ，et al.Hybrid entry guidance for reusable launch vehicle［J］.Journal of Astronautics，2007，28(1):213-217

［4］ Saraf A，Leavitt J A，Chen D T，et al.Design and evaluation of an acceleration guidance algorithm for entry［J］.Journal of Spacecraft and Rockets，2004，41(6):986-996

［5］ Calise A J，Rysdyk R T.Nonlinear adaptive flight control using neural networks［J］.IEEE Control System Magazine，1998，18(6):14-25

［6］ Hall C E，Leavitt J A，Chen D T，et al.Design and evaluation of an acceleration guidance algorithm for entry［J］.Journal of Spacecraft and Rockets，2004，41(6):986-996

［7］ 阮春荣.大气中飞行器的最优轨迹［M］.北京:北京宇航出版社，1987

［8］ 郑总准，王永骥，吴浩，等.基于FCMAC干扰观测器的动态逆再入制导［J］.华中科技大学学报，2010，38(1):96-100

［9］ Lin C M，Chen L Y，Chen C H.RCMAC hybrid control for MIMO uncertain nonlinear systems using slidingmode technology［J］.IEEE Transactions on Neural Networks，2007，18(3):708-720