敏捷卫星快速姿态机动方法研究

王淑一，魏春岭，刘其睿

(1.北京控制工程研究所，北京，100190;2.空间智能控制技术重点实验室，北京，100190)

国际上卫星技术发展十分迅速，从发展趋势上看，单颗卫星的功能日趋完善和复杂，具有快速姿态机动能力的卫星可完成更多的任务，受到各方关注［1］:利用敏捷姿态机动能力，在测绘领域可实现同轨立体成像，在空间对抗领域，可实现攻击载荷的快速瞄准，提高快速反应能力.国际上具有敏捷姿态机动能力的代表性卫星如 Pleiades、IKonos-2、Orb-View-3、WorldView等.Pleiades卫星是典型的敏捷卫星，采用太阳同步轨道，轨道高度694km，具有高敏捷的特点:俯仰和滚动通道的机动能力达到10s机动10°，25s机动60°，通过姿态机动可实现2天全球覆盖;卫星能提供多种图像产品:点目标图像、连续条带图像、拼接条带图像和立体图像.Pleiades卫星采用4个型号为CMG 15-45S(角动量15N·m·s，提供的最大力矩为45N·m)的控制力矩陀螺实现三轴姿态控制，CMG选用“金字塔”安装构形，框架轴与4个斜面垂直.

采用控制力矩陀螺群控制的卫星，要求姿态快速机动和快速稳定的同时，还要实现较高的姿态指向精度和姿态稳定度，为满足敏捷卫星快速机动和快速稳定控制，本文提出了一种按照欧拉轴-角方式、沿最小路径机动的轨迹规划方法，给出规划轨迹后，采用简单的PID控制律、利用CMGs即可实现敏捷卫星的快速姿态机动和稳定控制.

图1 Pleiades卫星和在轨机动飞行示意图

1 动力学及PID控制律

纵观国外敏捷卫星可知，一般敏捷卫星的刚性较好、多采用固定太阳翼、具有支杆结构，同时采用CMGs或者大力矩飞轮作为执行机构进行姿态机动控制.下面给出由CMGs进行控制的刚性系统的动力学模型［2］:

式中 J= [Jx，Jy，Jz]分别为卫星三轴转动惯量，ω=[ ωx，ωy，ωz]为 三 轴 姿 态 角 速 度，Td=[Tdx，Tdy，Tdz]为 三 轴 环 境 干 扰 力 矩，Tc=[Tcx，Tcy，Tcz]为CMGs产生的三轴控制力矩.

采用CMGs控制时，整个系统的控制框图简化如图2所示.

在大角度机动的情况下，由于用欧拉角描述姿态运动会导致奇异，因此这里用四元数描述星体的姿态运动.设相对轨道坐标系的规划四元数为qr，规划角速度在惯性系的表示为ωr，则误差角［3］和误差角速度计算如下:

为了满足快速机动的要求，在姿态机动阶段，构建了具有快速跟踪能力的前馈控制和大带宽的PD控制器，而在稳态运行时采用PID控制器，统一的控制器设计如下［4］:

其中:Kp为三轴比例控制系数矩阵，Kd为三轴微分控制系数矩阵，Ki为三轴积分控制系数矩阵.

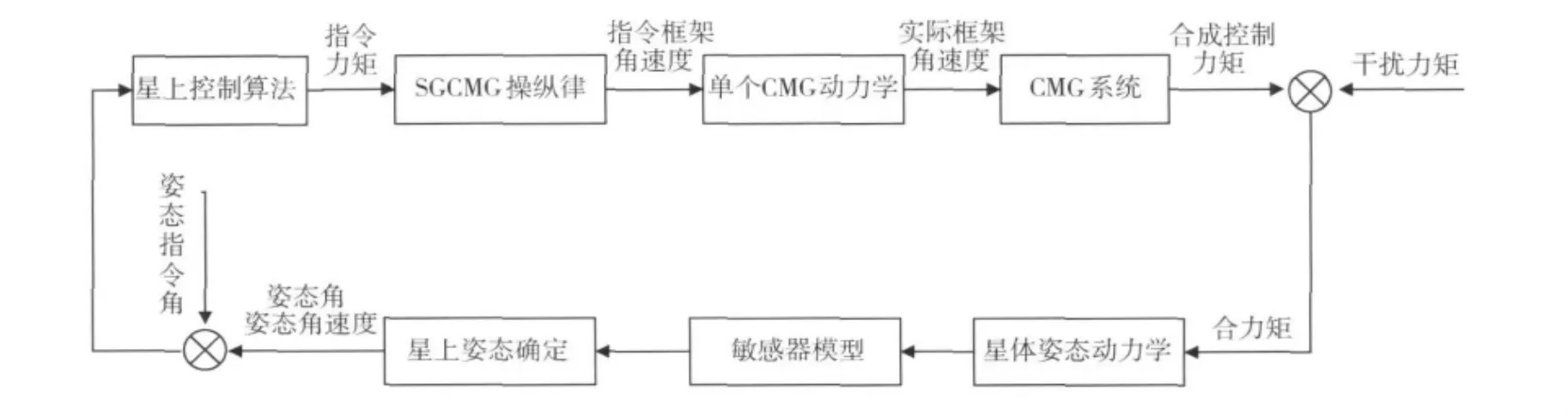
图2 控制系统框图

2 基于欧拉轴－角的轨迹规划

对于结构上近似刚体的卫星，采用大力矩飞轮和CMGs均能获得较高的转动速度，为了在较短时间内实现较大角度机动，需要对机动过程中的绕某特征主轴的角速度进行精细规划，缩短机动过程所需时间.下面基于欧拉轴-角方式，对沿特征主轴的机动角速度进行了三段式规划，设计出机动过程的四元数轨迹，实现对三轴大角度机动的跟踪控制.

2.1 特征主轴的计算

设机动起始点相对轨道系的四元数为q0，目标点相对轨道系的四元数为qt，则此次姿态机动的特征主轴四元数qbt0为:

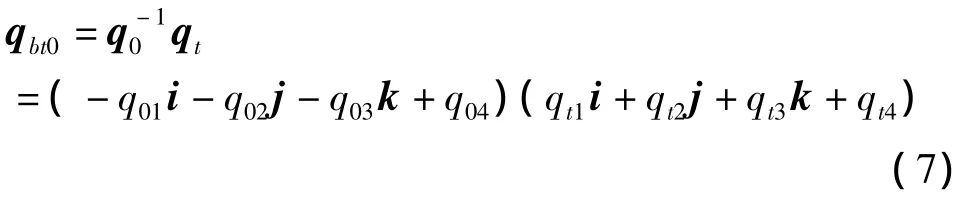
将此次机动的特征主轴(ix，iy，iz)在本体系表示为

2.2 角速度轨迹规划

不考虑稳定过程，为实现时间最优控制，应采用Bang-Bang控制，但考虑到系统受陀螺的测量范围和执行机构最大角动量包络限制，将卫星沿特征主轴的机动过程规划为加速、匀速、减速三段，规划出的沿特征主轴机动的欧拉角和角速度如图3所示.

图3 沿特征主轴的欧拉角轨迹示意图

图中，tm为姿态机动开始时刻;t1为姿态机动加速结束时刻;t2为匀速运动结束时刻;t3为机动结束时刻.卫星机动的实际角加速度a可根据执行机构能力确定.

姿态机动的规划角速度轨迹的转折时间点分别为

t1=tm+tr;tr为加速时间，可根据最大角加速度和陀螺测量量程等综合确定.

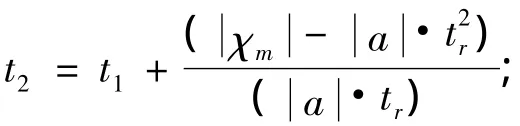
若t2＞t1，则有匀速运行段，此时:t3=t2+tr;

否则:t3=tm+2

2.3 目标四元数、角速度和补偿力矩计算

令规划后的相对初始四元数q0的机动四元数为qm，则

可得姿态机动过程中的规划四元数qr及规划目标角速度ωr分别为

为实现快速机动，可对姿态机动加减速段所需力矩进行前馈补偿，前馈补偿力矩公式如下:

其中J为星体转动惯量阵.

3 CMGs的操纵律设计

为保证卫星的敏捷机动性能，卫星平台的重量、功耗往往受到限制，通常仅配置4个SGCMG，4个SGCMG的构型中，一般以金字塔［5］构型为最优，这里也选用金字塔构型的CMGs.

图4 CMG金字塔构型图

由于控制力矩陀螺群构型限制以及CMG个数的限制，系统机动过程中可能出现构型奇异.系统中采用奇异鲁棒伪逆操纵律［6］，可以避开框架“锁死”现象，取

式中，C为陀螺群的雅克比矩阵，令各SGCMG的转子角动量相等，记为h.其中E3=εj(j=1，2，3)为适当选择的小量，λ为需要设计的标量参数.由于引入权系数，鲁棒伪逆控制律含小量力矩误差，但在奇异点处仍有可控性，在非奇异处，εj可为零，当det(CCT)趋向于零时，则εj增大.

4 数学仿真

以一个轨道高度为700km的太阳同步轨道卫星为例，轨道倾角为98°;星体机动的最大角速度取为2(°)/s;控制器系统的阻尼比取1.0，系统带宽0.3Hz;设置初始三轴姿态角均为0°，机动的目标姿态为滚动角45°，俯仰10°，偏航角0°;机动到位稳定一段时间后，再回零姿态，从仿真结果看，机动到稳态时间不超过35s.

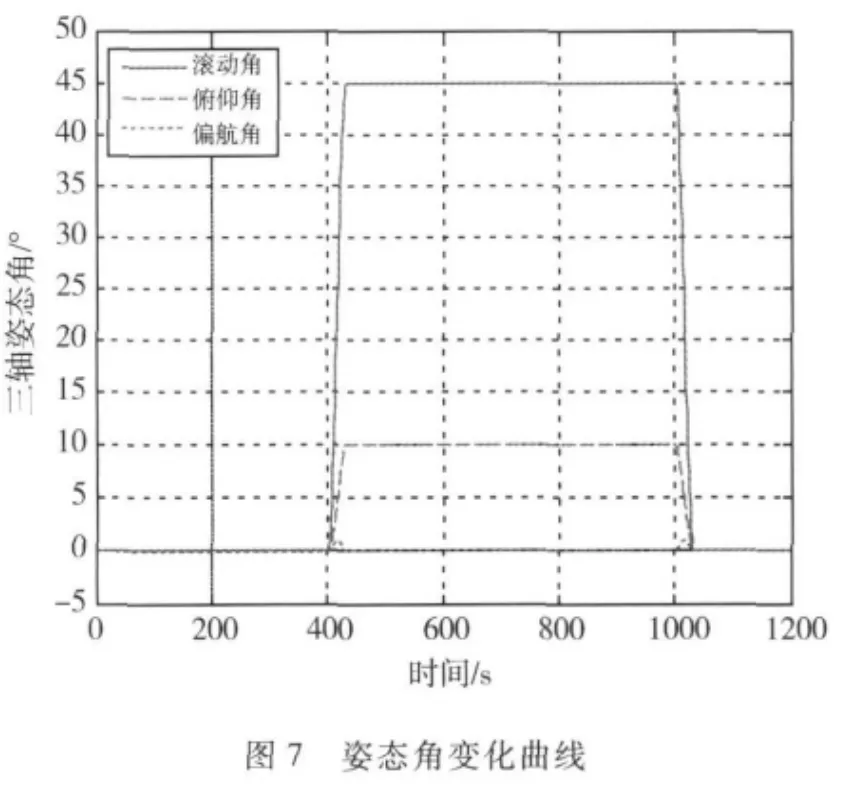
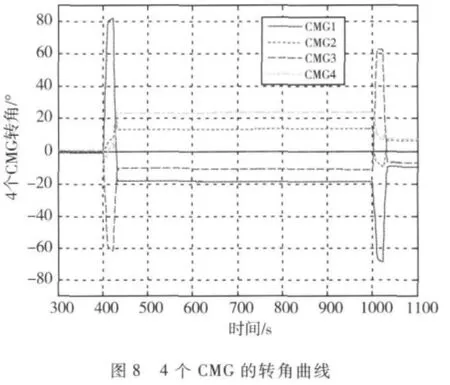
按照前述姿态机动策略和控制律，星体三轴姿态角和姿态角速度变化曲线如图5～7所示，CMG转角曲线如图8所示.

从上述仿真结果可以看出，通过对机动过程进行三段式规划，能够缩短机动过程需要的时间，并为机动到位后的稳定过程提供较好的初始条件.

图5 过程中姿态角速度变化曲线

5 结论

本文研究了一种基于CMGs控制的三轴大角度姿态机动方法，给出了基于欧拉轴-角的三段式轨迹规划，沿特征主轴按给定的欧拉角轨迹规划出机动四元数，采用简单的PD控制律实现了三轴大角度姿态机动.数学仿真表明:该机动策略可实现三轴大角度快速机动，并为快速稳定提供较好的初时条件.对于快速机动的敏捷卫星而言，是一种简单可行的机动策略.

［1］ 吴忠，吴宏鑫.“和平号”空间站SGCMG系统及其操纵律［J］.航天控制，1999，17(2):76-80

［2］ 章仁为.卫星轨道姿态动力学与控制［M］.北京:北京航空航天大学出版社，1998

［3］ 韦娟，宁方立.误差四元数及其在航天器姿态控制中的应用［J］.飞行力学，2006，24(2):60-62

［4］ 汤亮，徐世杰.采用单框架控制力矩陀螺群的卫星侧摆机动控制研究［J］.航天控制，2003，21(2):1-6

［5］ Gmargulies A J N.Geometric theory of single-gimbal control momnet gyro system［J］.The Journal of the Astronautical Sciences，1978，(2):159-191

［6］ 刘付成.一种改进的SCMGs奇异鲁棒伪逆操纵律算法［J］.上海航天，2009，26(2):1-8