车身的模态分析及疲劳寿命计算

2011-04-10毛彩菊

制造业自动化 2011年11期

毛彩菊，王艳

MAO Cai-ju1,WANG Yan2

（1. 南京信息职业技术学院，南京 210046；2. 中国地质大学长城学院，保定 071000）

0 引言

随着对汽车舒适性要求的不断提高，汽车的振动逐渐成为人们所关注的重要指标之一。对承载式轿车车身，其动力学特性很大程度地影响着整车的平顺性，用计算机分析以及通过试验辨识车身的动态性能，并根据实验结果提出相应的优化设计方案，是提高汽车平顺性的关键。

模态分析是动态分析的前提，是动态分析的主要组成部分。对车身进行模态分析可以了解车身对激振力的响应，从而对车身优化设计方案的动态特性进行分析，是车身设计过程中关键的设计环节。过去研究车身结构的模态特性通常利用试验模态方法，该方法的缺点是耗时多、实验方法复杂、实验耗资多，无法满足车身的设计和开发初期就对乘坐舒适进行控制和评价的要求。有限元技术作为一种新兴的技术正在不断地发展，为车身的开发设计提供了有效的模态分析的方法，为控制车身的固有频率与振型提供了技术支持。依据模态分析理论，对于大型的结构，只需求出前几阶固有频率和相应的振型，因为对车身动力特性影响最大的是低阶振动。利用有限元分析平台ANSYS软件对车身进行模态分析，并对其动态特性进行评价。

另外，汽车的疲劳寿命计算也是提高整车性能重要因素，利用有限元技术对车身进行疲劳寿命评估是一种高效的方法，通过车身疲劳寿命的计算，可以为车身的优化设计提供有利的理论依据。

1 有限元模型的建立

1.1 模型的简化

对于全承载式车身结构车型，车身骨架属于关键的承载体，各种载荷通过骨架将力传递到车身的不同位置，使得整个车身都承担承载。由于车身骨架不仅是一个非常复杂的空间薄壁结构，而且包含大量的应力蒙皮，然而一些非关键的承载部件对骨架结构的变形和应力分布没有太大的影响，而对分析的效率和可靠性却影响很大。所以，在进行有限元建模的时候，可以对车身进行必要的简化，进而可以提高计算的效率和正确性。

1）忽略一些无关紧要的非承载件：对于某些方便使用和辅助承载而设置的构件（如：扶手、裙部、制动踏板支架等），因为这些部件对车身的变形和应力分布几乎没有影响，可以忽略。

2）车身表面光顺化：车身表面上的孔、台肩、凹部和翻边等在条件允许的情况下可以忽略使表面光滑。

3）主从节点原则：出于对结构模型病态问题的考虑，对于位置较近的构件结合点则采用适当合并或“主从节点”的方式处理，避免仿真过程中可能会引起的方程病态。

4）蒙皮处理：蒙皮是对骨架刚度加强作用不大的结构，不考虑应力蒙皮的加强作用。

5）载荷分配：载荷的分配直接影响计算结果，应对地板、乘客、座椅及行李等质量做合理的分配，使之作用在适当的位置。

1.2 车载质量的处理

车身骨架的车载质量主要是动力总成、备用轮胎、散热器、压缩机、油箱、司机座椅、乘客及卧铺、行李箱、清洁水箱、卫生间等。通常可以根据车载质量的空间布置情况将它们换算成节点载荷施加在其布置位置的节点上，但这种处理方法在车身受侧向或纵向加速度作用时，不能考虑到这些质量对车身骨架侧向载荷的贡献。所以，把部分空间位置上比较零散的质量(比如，乘客、卧铺、行李等)，用质量单元直接设置在车身支点位置的结点上，支点所设置的质量单元的质量为该支点实际承受的质量，惯性矩为该支点实际承受的质量对该支点的惯性矩；将质量分布比较集中的载荷(比如，发动机、油箱等)，在设备质心位置创建质量单元，其质量等于该设备的质量，然后将该质点与设备的支撑点刚性连接起来。

2 有限元分析理论基础

2.1 基于有限元技术的模态分析

利用ANSYS软件的模态分析模块对车身进行固有频率计算，可以根据计算结果对车身的振动性能做出评价，是分析车身动态特性的有效方法。模态分析用于确定车身结构的振动特性（固有频率和振型），它们是承受动态载荷结构设计中的重要参数。在进行车身的模态分析中，采用区块Lanczos法，不考虑阻尼影响的系统自由振动方程是[3,4]：

式(1)的解可以假设成以下形式：

式中：φ为n阶特征向量，m；ω为向量φ振动的频率，Hz；t为时间变量，t0为由初始条件确定的时间常数，s。

将式(2)代入式（1），就得到广义特征值问题：

求解以上方程可以确定φ和ω，结果得到n个特征解(ω12,φ1)、(ω22,φ2)、…、(ωn2,φn)，其中特征值 ω1、ω2、…、ωn代表n个固有频率，并有0≤ω1〈ω2〈...〈ωn，特征向量(φ1,φ2,...,φn) 代表了n个固有频率的振型。

2.2 基于有限元技术的疲劳分析

对车身进行疲劳寿命计算时，可以利用ANSYS软件的疲劳分析模块，这是一种简洁、有效的方法。在进行疲劳寿命计算时，利用了简化的弹塑性假设，并采用Miner累积疲劳求和法则，其计算过程有以下几个步骤[5,6]：

1）定义材料疲劳特性：在计算使用系数时，应该考虑材料的弹塑性性质，而且要定义材料的疲劳特性。在ANSYS软件中是利用材料的S-N曲线的方法，也就是材料的最大的应力强度与应力循环次数的关系曲线。在计算过程中，首先将已知的S-N曲线输入ANSYS疲劳分析模块中。

2）选择疲劳分析点，定义应力集中系数：利用ANSYS软件进行疲劳寿命计算时，需要确定疲劳计算的节点位置，并且给定计算位置的应力集中系数，而应力集中系数通常是依据指定位置的形状变化来决定的。

3）存储计算点的应力值：车身在受到撞击力时，损伤位置会产生很大的应力，在加设置载荷事件时通常采用两载荷个步。第一个载荷步为零载荷步，应力值可以通过手工输入；第二个载荷步是最大的额定载荷，节点的载荷值可以从静应力的结果数据库读取。

4）疲劳计算：利用ANSYS软件对车身进行疲劳寿命计算之前，车身应该满足109次数量级的应力循环的要求，因此疲劳计算前，赋予载荷时间109次的循环数。

上面四个步骤都完成之后，就可以直接利用疲劳模块进行疲劳寿命计算了。

根据车身在实际运行中的受力状态，可知其疲劳应该是低周疲劳。利用ANSYS软件的疲劳分析模块对车身进行基于有限元技术的疲劳分析是十分有效的方法，可以进行车身的疲劳寿命的预测计算分析，最终能有效地预测出疲劳寿命次数。

表1 车身的前6阶模态分析结果（单位：Hz）

3 车身的有限元分析

3.1 车身的模态分析

根据该车身的结构，应该选择抗压，尤其能抗弯曲和扭转的单元进行网格划分，因此，板壳单元是比较理想的选择。由于该车身有许多装配工艺孔、过渡圆角等细小结构，这些结构对车身整体性能影响不大，同时为了能提高计算效率，在进行有限元分析时，可以将这些细节忽略不计。在有限元分析软件ANSYS中，选用shell63单元。该单元有4个节点，每个节点有6个自由度，各节点上的厚度可以不等，这种参数的没置能构成一个变截面的壳单元。

图1 车身结构示意图

网格类型与有限元计算所需时间以及计算精度有着直接的关系，因此确定网格类型是有限元建模的一个很重要的方面。三角形单元的适应性好，能划分各种复杂形状的模型，且计算速度快，但计算精度不高，可以作为划分的基本分网工具。四边形单元精度较高，适用于静动态分析的细致计算，但进行自由网格划分网时易产生畸变网格，导致计算的失败，考虑到本文中车身曲面的复杂程度和计算精度要求，最终采用两种单元共同来划分网格。整个车身模型共划分16584个节点，12347个单元，划分网格后的模型如图2所示。

图2 车身的有限元模型

3.1.1 基于ANSYS的车身模态分析

利用ANSYS软件，利用BLOCK LANCZOS方法对车身进行模态分析，取前6阶进行研究，其计算结果如表1所示，各阶固有频率所对应的振型如图3所示。各阶固有频率所对应的振型为分别为：

1）第一阶振型：车身前顶棚局部振动；

2）第二阶振型：车身后顶棚局部振动；

3）第三阶振型：车身一阶扭转；

4）第四阶振型：车身一阶弯曲；

5）第五阶振型：车身前梁局部振动；

6）第六阶振型：车身侧面局部振动。

图3 车身前6阶固有频率所对应的振型

该车前6阶固有频率集中在8.3-19.8Hz之间，根据实验可知，该车车身共振频率在5.3-7.8Hz之间,发动机怠速频率约为20-26Hz之间，因此车身低阶模态频率需要在8-20Hz之间。而该车身发生一阶扭转振型时的固有频率为9.7Hz，发生一阶弯曲振型时所对应的频率为12.9Hz，通过模态分析实验结果可知，该车车身的固有频率恰巧落在了所必须的频率范围内，可以有效地避免发生车身的共振。

3.1.2 车身的实验模态分析

车身的实验模态分析可以通过采集车身的输入输出信号参数识别对车身的模态参数进行测量。操作方法如下：首先在车身静止的状态下给其施加激振力，通过对激振力和振动响应的测量，获得激励点和各个测量点间的传递函数，然后可以形成传递函数矩阵。最后通过对传递函数的曲线拟合，根据模态分析理论识别车身的模态参数。

车身的模态分析试验系统主要有以下几个组成部分。激振部分：该部分主要由功率放大器、信号发生器和激振器构成；振动信号测试和数据采集系统部分：该部分由阻抗头、速度传感器、电荷放大器和数据转换和记录器构成；信号分析和频响函数分析部分：该部分由模态分析软件和电脑构成。

为了能够保证系统可靠稳定，在实际测试前采取单点激振和双点激振的方式进行预测试，保证试验系统各个部分无异常。将车身线框图导入模态分析软件中，定义好车身几何点，同时依据车身的实际结构和测试点的安排规律确定所有测试点，将车身的前纵梁位置定义为测试点，利用双点激振的方法，利用随机信号作为激振信号。

在车身的模态实验分析的实验中，数据采样频率取为1024Hz，设定分析频率为300Hz，拾振传感器取为12个，采取移动传感器的方式进行分批测量。车身的测试点试验数据的采集和频响函数的分析同时进行，同步观相干函数和频响函数，相干函数在0.95以上为有效数据，相干函数紊乱的测试点无效，需要重新测试。每个测试点实施40次激励，然后取它们的均值使用，这样能够提高测试精度，减少测试误差。

通过测试可以求出车身的前6阶固有频率，其结果如表2所示。

表2 车身实验模态分析的前6阶模态测试结果(单位：Hz)

从车身的实验模态分析结果可以看出，测试的固有频率和有限元分析的结果误差均控制在4%以内，验证了有限元分析结果的正确性，并且为有限元计算模型的设计提供了依据。

3.2 车身的疲劳寿命计算

3.2.1 材料的S-N曲线

该车身为钢制造车身，通过查金属材料手册绘制出了车身制造材料的的S-N曲线，如图4所示。

3.2.2 疲劳计算参数

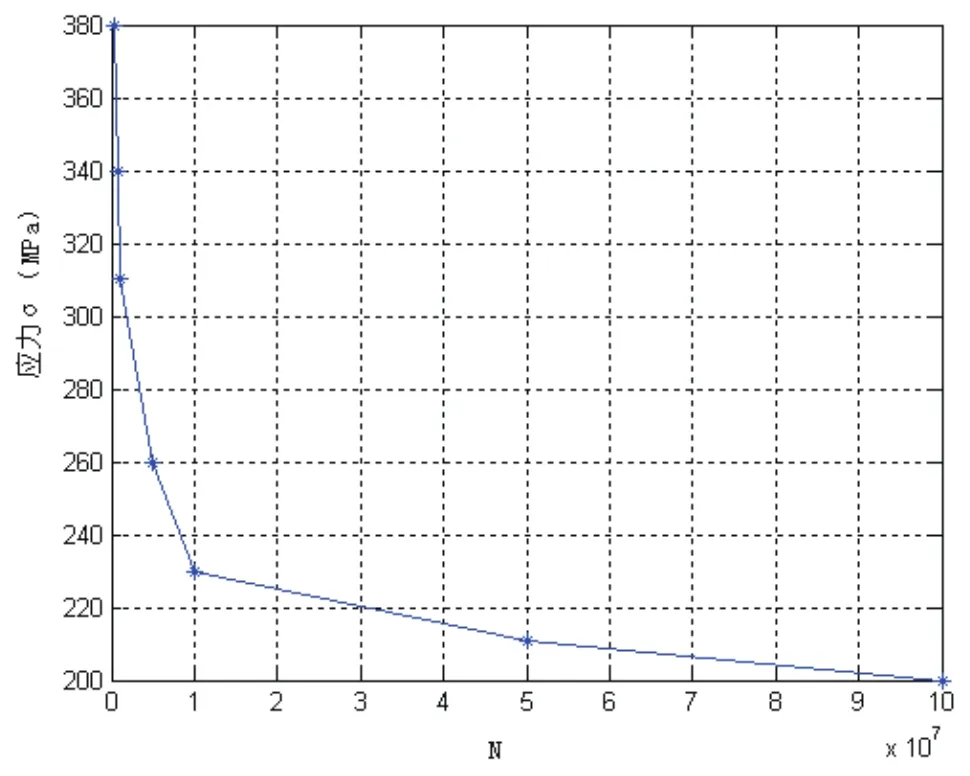
图4 车身制造材料的S-N曲线

可以利用平均应力修正寿命法对事故车车身进行疲劳寿命计算，所采用的模型主要有S-N曲线模型和以下几个理论模型：

Goodman直线力学模型：

其中，σmax为最大应力；σ-1为疲劳极限；σm为平均应力；σb为静强度；σs为屈服极限。3.2.3 疲劳寿命计算结果

利用上述力学模型计算疲劳分析参数设置，在ANSYS的疲劳分析模块中进行计算，最后得出结论。其计算结果如表3所示。从表中可知，利用S-N线性模型计算结果的最小，利用Gerber抛物线力学模型的计算结果最大，利用Goodman直线力学模型的计算结果介于上述两种模型的计算结果的之间。疲劳寿命的差异是由于这三种模型的假设以及计算误差导致的。对同类型的车身进行统计，表明疲劳计算结果与实际的车身疲劳寿命基本吻合。