对水波干涉图样成因的再认识

马新亚

(宿州第二中学 安徽宿州 234000)

当两列周期相同的水波相遇时，在它们重叠的区域里，水面上出现了一条条相对平静的区域和剧烈振动的区域．这两种区域在水面上的位置是稳定不变的，而且平静的区域和剧烈振动的区域交替出现．对于上述水波干涉图样的形成原因，教材上给出了这样的解释:“如图1所示，两组同心圆表示从波源发出的两列波的波面，实线圆表示波峰，虚线圆表示波谷．如果在某一时刻，水面上的某一点(如图1中的a点)是两列波的波峰与波峰相遇，那么经过半个周期，一定是波谷与波谷相遇．波峰与波峰相遇时，质点向上的位移最大，等于两列波的振幅之和;波谷与波谷相遇时，尽管质点的位移是向下的，但也是最大，也等于两列波的振幅之和．因此，在这一点，两列波引起的振动始终是加强的，质点的振动最剧烈，振动的振幅等于两列波的振幅之和．如果在某一时刻，水面上的某一点(如图1中的b点)是两列波的波峰与波谷相遇，经过半个周期，就变成波谷与波峰相遇．在这一点，两列波引起的振动始终是相互削弱的，质点振动的振幅等于两列波的振幅之差．如果两列波的振幅相同，质点振动的合振幅就等于零，水面保持平静．虚线圆与虚线圆的交点，或者实线圆与实线圆的交点，是振动加强区，它们连成的区域用粗实线画出;虚线圆与实线圆的交点为振动的减弱区，它们连线的区域用粗虚线画出．从图1中可以看出，情况与实验结果是一致的．”

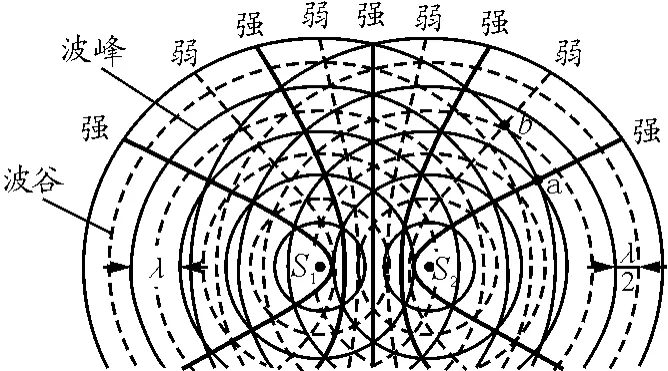
图1

对于这样的解释，学生提出问题:“为什么虚线圆与虚线圆的交点，实线圆与实线圆的交点的连线上的所有点都是振动加强点，虚线圆与实线圆的交点的连线上的所有点都是振动减弱点?加强区和减弱区为什么会如图中所示那样稳定且交替的分布?”

2 对水波干涉图样成因的解释

2． 1 平面简谐波的波动方程

平面简谐运动在一个方向上传播所形成的波，叫平面简谐波．若已知一列横波(纵波情况类似)以速度v沿x轴正向传播，波源O点的振动方程为

这就是波动方程．

2． 2 振动加强点和振动减弱点形成的条件

如图2所示，设两相干波相遇区域中任一点P到两相干波源S1和S2的距离分别为r1和r2，波源S1和S2的初相位分别为φ1和φ2，则两相干波在P点引起的两分振动的相位差为

两相干波在P点引起的合振幅为

当Δφ=2nπ时，A=A1+A2在该处发生相长干涉;

当 Δφ =(2n+1)π 时，A= │A1－A2│，在该处发生相消干涉．

图2

2． 3 振动加强点和振动减弱点连接形成的线的曲线方程

对于图2中所示的干涉，波源S1和S2同频率、同振动方向、同相位，距离波源为r处的点的振动方程为

设两相干波相遇区域中任一点P到两相干波源S1和S2的距离分别为r1和r2，则两相干波在P点引起的两分振动的相位差为

两相干波在P点引起的合振幅为

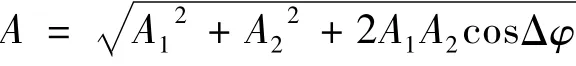
当 Δφ =2nπ，亦即当│r2－ r1│ =nλ(n=0，1，2，3，…) 时，A=A1+A2在该处发生相长干涉;

当Δφ =(2n+1)π，亦即当 │r2－r1│ =该处发生相消干涉．

现以S1和S2连线的中点O为坐标原点，以S1和S2连线为x轴，以过O点且垂直S1和S2连线的直线为y轴建立平面直角坐标系．设S1和S2的间距为d，现分几种情况叙述振动加强点满足的曲线方程．

(1)若│r2－r1│ =0，则加强点满足的曲线为y轴，曲线方程为x=0．

(2)若│r2－r1│ =λ，则加强点满足的曲线方程为

(3)若│r2－r1│ =nλ，则加强点满足的曲线方程为

从以上的讨论中可以看出，所有振动加强点连成的线是一系列不连续双曲线，且到两相干波源S1和S2距离差越大的点对应的双曲线，其中心线越偏离S1和S2连线的中点O，且其渐近线斜率越小，以上结论同样适用所有振动减弱点连接形成的线．

综上所述，同频率、同振动方向、同相位的两波源S1和S2所形成的波在相遇区域中叠加，所有到S1和S2距离相等的点形成振动加强区，该区域在S1和S2连线的垂直平分线上;所有到S1和S2距离相差半个波长的点连线形成振动减弱区，该区域分布在以S1和S2连线的中点O为对称的双曲线上，曲线中心到中点O的距离为半个波长．所有到S1和S2距离相差一个波长的点连线形成振动加强区，该区域分布在以S1和S2连线的中点O为对称的双曲线上，曲线中心到中点O的距离为一个波长，曲线所对应的渐近线的斜率更小一些．以此类推便形成了教材上的水波干涉图样．