起重机超静定杆系结构弹性稳定分析中的有限元误判与应对

孟丽霞，陆念力，胡燕东

（哈尔滨工业大学 机电工程学院，黑龙江 哈尔滨 150001）

随着材料科学的迅猛发展，高强度结构钢开始广泛应用于大型起重运输与工程机械和建筑结构中，此时相对于结构的强度和刚度验算而言，起重机金属结构的稳定性校核的重要性愈加凸显.起重机设计规范中除了要求验算整体稳定的同时，还要求验算各杆件的局部稳定［1］，很多文献从不同角度对结构整体失稳和局部失稳的计算方法进行了探讨［2，3］.桁架结构向实腹式结构等效的稳定性计算方法、不同结构形式对整体失稳和局部失稳的影响以及整体稳定和局部稳定临界力的关系等问题受到了普遍关注［4-7］.

有限元法及其应用软件是大型复杂桁架结构计算分析的最有效方法.随着工程中有限元方法的广泛普及，越来越多的设计人员直接采用有限元法这一先进的计算手段进行机构的强度、刚度和稳定性分析，大大地提高了计算精度和效率［8］.通常的有限元方法及其应用软件虽可较好地解决结构强度和刚度分析问题，但对结构稳定性极限状态的判断尚无很好的手段.用ANSYS等现有的有限元应用软件对结构进行稳定性分析时，不区分整体失稳和局部失稳，只一概而论地称之为失稳.对静定桁架结构而言，单肢失稳就意味着整体失稳，因为静定桁架中任何1根杆件的失效，整体将成为几何可变体系，结构丧失原有稳定工作形态，也因此失去原有的承载能力.对超静定结构则未必，单肢或局部失稳后，结构受力条件会发生变化，产生局部失稳后的载荷重新分配.因此，当采用有限元法对超静定桁架结构进行稳定性分析时，得到的失稳临界力并非真正的结构失稳时的极限载荷，有时整体结构真实失稳临界力远大于局部失稳临界力.在工程中设计人员更关心结构实际能够承受的稳定临界载荷，即整体结构何时出现失稳，它是确定结构稳定性的安全储备、优化结构设计的依据.

1 梁杆系统精确有限元方程及其在稳定性分析中的应用

1.1 有限元特征值屈曲分析的理论基础

结构稳定性的能量准则表述为：弹性力学系统总势能Π的正定二阶变分是保证结构静力稳定的必要和充分条件，即：

式中：δ为对势能Π求变分，即δ2Π表示对Π求二阶变分.

在有限单元组成的结构中，若不考虑初始缺陷，结构总势能表示为

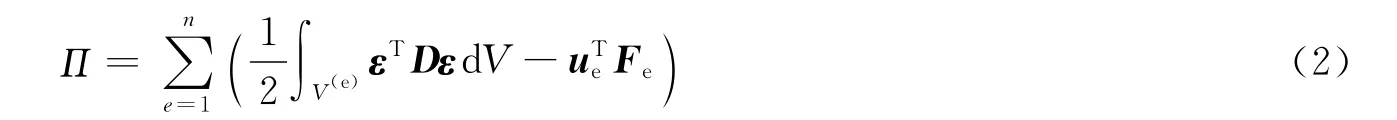
式中：V（e）为单元体积；ε为单元应变列阵；D为单元弹性矩阵；ue为单元位移列阵；Fe为单元节点载荷列阵.

总势能关于节点广义位移向量u的二阶变分为

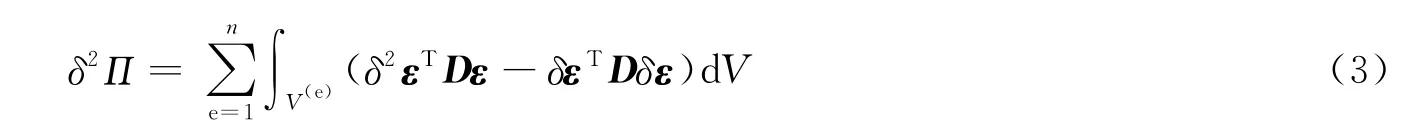
由非线性有限元理论得

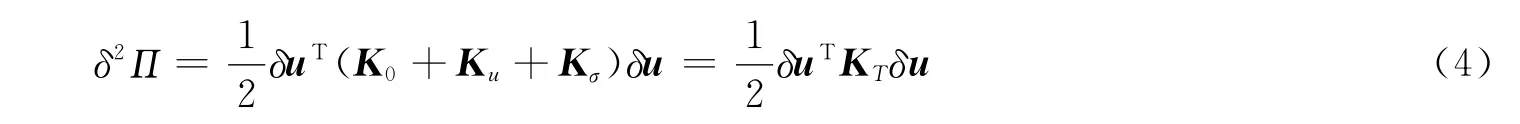
式中：K0为线性刚度阵；Ku为大位移刚度阵；Kσ为几何刚度阵；KT为切线刚度阵.

可见，总势能Π的二阶变分δ2Π＞0与正定的KT是等价的.因而结构失稳的临界条件也可以表示为

在弹性稳定所涉及的小变形情况下，略去大位移刚度阵Ku，式（5）可表为

Kσ是关于系统载荷的函数，由此可解得整体结构的临界载荷.对于线性屈曲问题，屈曲前的结构处于初始模型的线性平衡状态，应力和外载也为线性关系.如果令结构处于某一载荷状态下的几何刚度矩阵为，则由线性关系将式（6）改写为

1.2 基于二阶理论的梁单元精确刚度阵

由上述分析可知，有限元法求解稳定问题的精度取决于切线刚度阵KT的精确度.文献［5］运用二阶理论给出了梁单元精确刚度阵：

这就是一般有限元软件中所用的梁单元切线刚度阵.

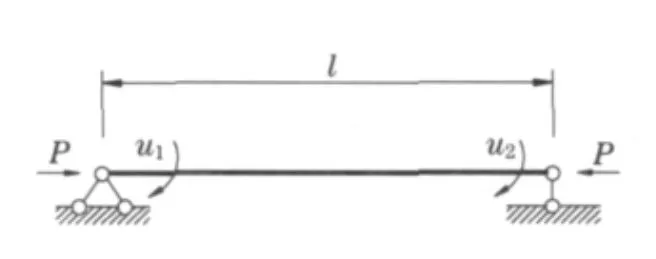
图1 2端简支轴向受压的铰支杆Fig.1 Simply supported column with axial force

1.3 典型结构的失稳算例

图1为2端简支轴向受压的铰支杆，2端承受轴力P作用，分别产生角位移u1，u2.此结构中只有1个单元，由精确刚度式（8）得其刚度阵为

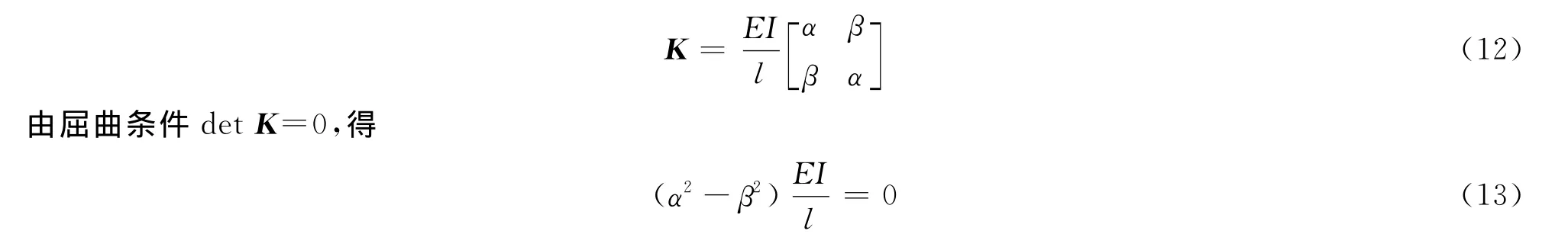
由屈曲条件det K＝0，解得临界力Pcr＝12EI／l2，与精确解误差达21.6%.当把构件划分为2个单元时，误差可减至0.7%.

2 有限元法在超静定杆系结构弹性稳定分析中的误判

如前所述，有限元方法判断结构失稳的依据是系统切线刚度阵的行列式值为零.这其中并无局部失稳、单肢失稳或整体失稳的考虑.有限单元法是解决复杂结构分析问题的强有力工具，已成为共识.随着计算机速度与容量的提高，以及各类结构分析软件的出现，人们对有限元软件的信任与依赖越来越大.在ANSYS等成熟的著名商用有限元程序为人们解决了一个又一个复杂的结构分析难题时，除对自身应用软件建模能力不自信之外，极少有人怀疑有限元方法及分析软件本身可能带来的问题.但当涉及梁杆系统超静定结构稳定分析时，不得不重新冷静地审视有限元方法本身带来的问题.

考察图2a中的二单元超静定结构的稳定性，设杆1、杆2的截面积为A1＝A2，截面惯性矩为I2＝3I1，承受轴力N 作用.直接用解析法可得系统的临界力为

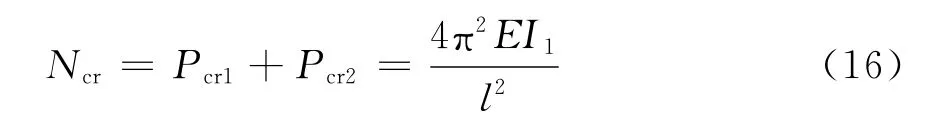
而用有限元方法计算的系统临界力为

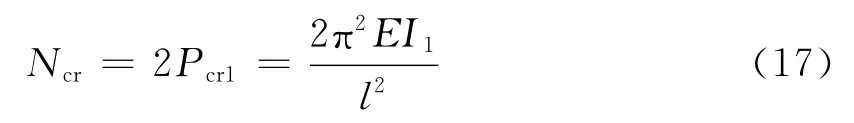
显然有限元方法计算系统临界力是错误的，因为系统临界力居然小于杆2单独的临界力为

再考察图2b中的倾角相同、大小均为θ的对称二杆结构，当二杆截面积相等时，无论截面惯性矩是否相等，由解析法得到的系统临界力皆为

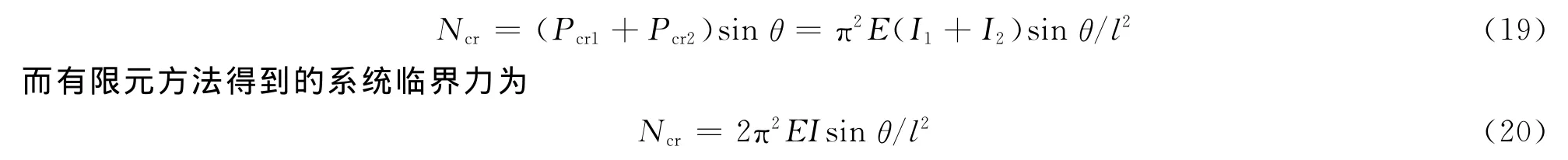
式（20）中，I为I1，I2中的较小者，显然与解析法得出的解有差别.

由这2个简单超静定结构实例不难发现，当结构中某根杆件首先失稳时，有限元程序即给出整体失稳的判断，这是典型的误判.

考察图3中的二单元静定结构和图4中的三单元超静定结构，均承受轴力P作用.设2图中杆1、杆2的材料参数相同，均为φ20mm的钢管，图4中杆3材料使用φ12mm的钢管.运用有限元软件ANSYS和SAP计算，得到图3的二单元静定结构屈曲载荷为120.47kN，图4的三单元超静定结构屈曲载荷为51.628kN.三单元超静定结构多了1根构件，其他结构与二单元静定结构相同，可是有限元软件算出的屈曲载荷居然比二单元静定结构屈曲载荷低得多，显然又是误判.

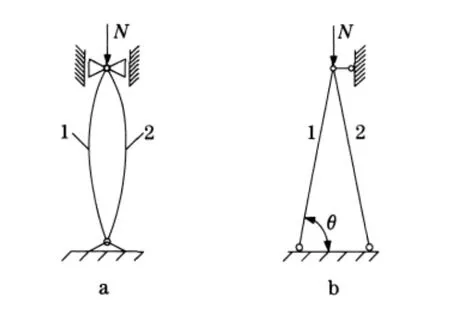
图2 二单元超静定结构Fig.2 2-element statically indeterminate structure

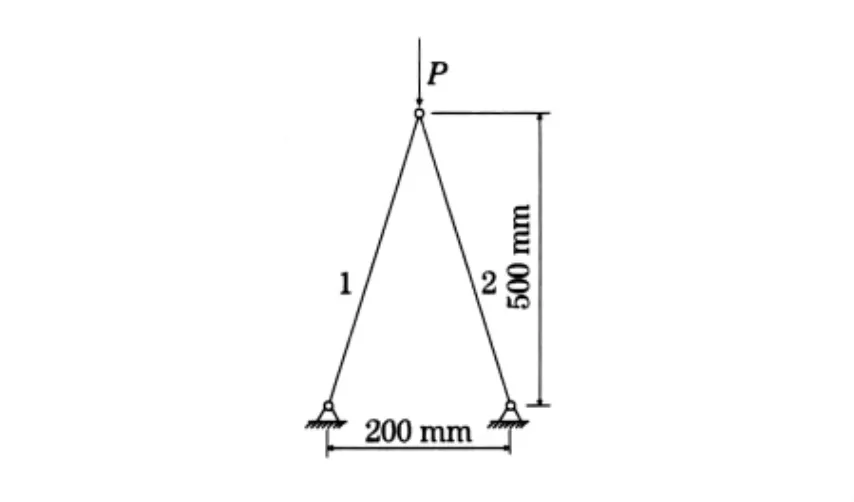
图3 二单元静定结构图Fig.3 2-element statically determinate structures

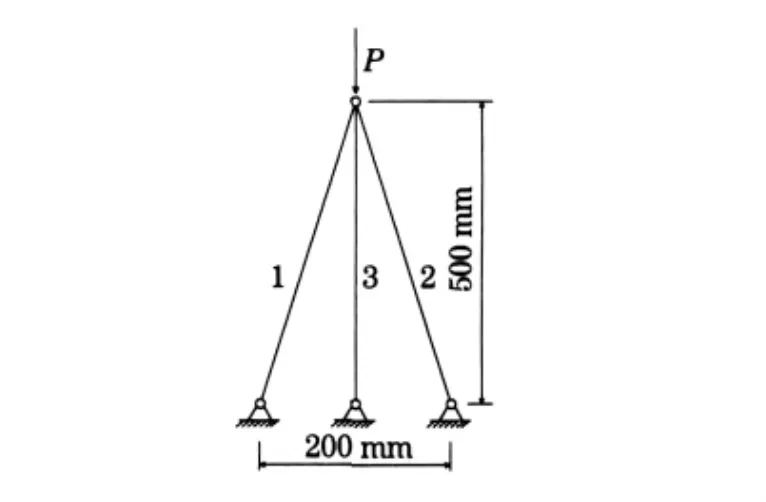
图4 三单元超静定结构Fig.4 3-element statically indeterminate structure

有限元工具在面临超静定梁杆结构时，出现了误判.而工程机械结构中又是如此广泛地使用超静定梁杆架结构，并如此倚重有限元工具，这是不得不重视的问题.采用有限元方法分析静定梁杆结构的稳定性时，如何克服通用有限元软件在计算超静定结构稳定临界力时的“误判”至关重要.为此，首先须找出导致误判的原因.

既然有限元方法判断结构失稳的依据是系统切线刚度阵的行列式值为零，那么根源就在系统切线刚度阵的构成上.由较为简单的图2二单元结构着手，系统的切线刚度阵可表为

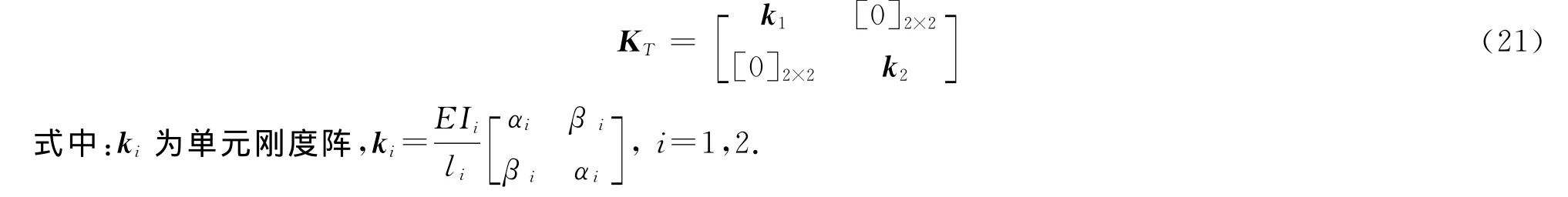
系统失稳条件式为

从式（12）中可知，这是2个铰接杆单元刚度阵行列式值的乘积，无论哪个单元刚度阵行列式值先为零，系统都将宣告失稳，误判由此产生.

考察任意2端铰接杆单元刚度参数在系统刚度阵的位置，不难得知，单元的端部转动自由度独立于系统的其他自由度，其转动刚度与系统其他单元刚度不发生耦合.不失一般性地对系统刚度阵施加不改变整体刚度矩阵行列式值的初等变换，总可获得形如下式的等效整体刚度矩阵：

由式（24）可见，各铰接杆单元刚度阵行列式是独立无关的，无论哪个单元刚度矩阵的行列式值先为零，系统都将宣告失稳，而系统的整体失稳则取决于A的行列式.要消除稳定性临界力误报，就必须找出小于整体失稳载荷的失稳单元.

3 超静定桁架结构稳定性误判消除的单元撤换法

由前述分析可知，超静定桁架结构的整体稳定临界力出现误判的原因，是有限元方法中当单元刚度矩阵行列式为零（单元失稳）时，导致整体刚度矩阵行列式为零，出现整体失稳的误判.因此，1个直接有效的消除误判方法就是：将单肢失稳的单元去除，而在单元2端代之其可承受的欧拉临界力.例如，作为原超静定的桁架结构，如图5a所示，去掉1个多余杆件仍为超静定结构，如图5b所示，图5b再去掉1个多余杆件变为静定结构，如图5c所示，该结构仍可继续承载.

超静定结构中某些杆件依次失稳，被代之以相应的单肢欧拉临界力，直至结构变成静定结构.这个具有预加载荷的静定结构的临界失稳载荷，即为原系统的临界力.单元撤换法的思路是很简洁、直观的，对简单结构可人为分析判断.但事实上实施起来并非易事，对高次超静定的复杂结构尤为如此.其难度在于，如何在众多的杆件中依次找出先行失稳的杆件，将其去除并代之以杆当前的轴力（即单元的欧拉临界力）.显然只能通过编程进行系统判断.虽然现有的通用商业有限元软件ANSYS，SAP84等在解决超静定桁架稳定性分析上存在误判的功能缺陷问题，但其程序组织、数学模型与力学模型的组装和求解功能的强大与成熟是众所公认的.因此，需合理利用ANSYS的程序内核，引入单肢失稳判断和处理方法，在ANSYS平台上构建新的有限元分析力学模型，进而求解新的系统临界力，依次消除各阶次超静定引起的误判，得到系统真正的弹性稳定临界力.

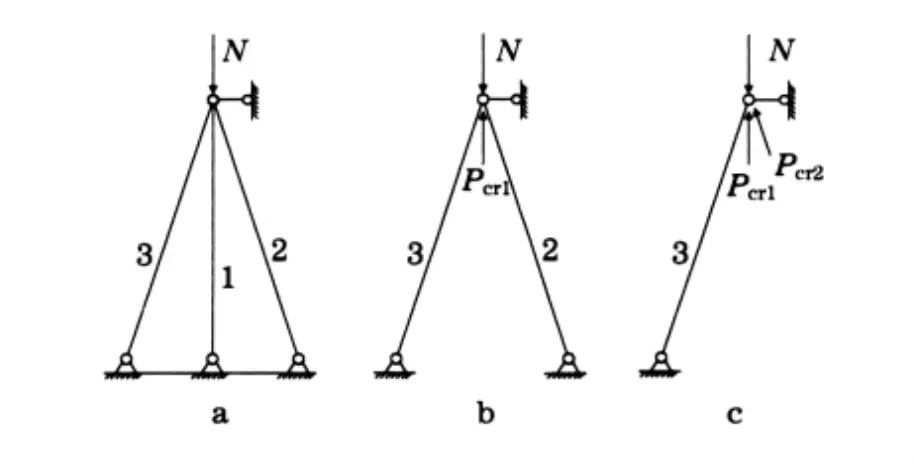
图5 超静定结构杆单元撤除法示例Fig.5 Demonstration of element replacement in statically indeterminate structure

4 基于ANSYS平台的杆系结构稳定性分析软件开发

如前所述，采用有限元软件计算所得的超静定桁架结构的失稳临界力未必是表征结构失稳临界状态的受力情况.为了得到这类桁架结构失稳的临界载荷，对通用的有限元分析软件进行二次开发在工程中有很大的实际意义.超静定结构在整体没有失稳之前杆件变形可用小挠度理论分析［9］，认为杆件的失稳是一类失稳来简化计算.当桁架结构出现单肢失稳时，如果继续增加载荷，失稳的杆件单元所受的内力保持临界值，并不会因外载增加而增加，此时，其他单元将分担全部增加的载荷.所以，从受力特性上来说，此时的结构已经发生变化，要继续分析结构是否还有承载能力，必须对有限元分析模型进行相应的改动，建立起与实际结构受力相同的等效结构模型.本文基于ANSYS环境进行二次开发，在进行稳定分析过程中对结果进行分析，判断ANSYS得到的临界状态是否为单肢失稳临界状态，并进一步建立等效分析模型，继续稳定性分析，直到得到结构整体失稳时的临界载荷.本文开发的程序流程如图6所示.

图7所示的交叉腹杆式塔式建筑起重机，每一面塔身腹杆交叉对称布置，受力量值大体相等，拉压相反.由于腹杆较纤细，杆件长细比很大，在有限元分析中很快就出现失稳.实际上把压杆去除后，另一受拉腹杆仍可单独提供结构的安全工作.运用本文提供的方法和分析程序，很好验证了这一点.

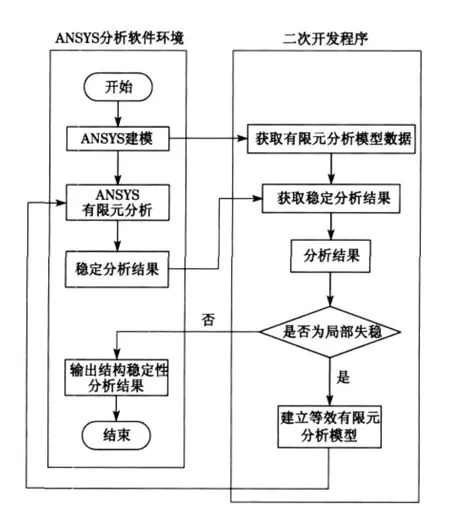
图6 基于ANSYS的杆系稳定性分析程序流程Fig.6 Program flowchart of stability analysis of truss structure based on ANSYS

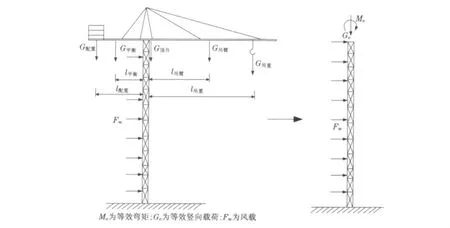
图7 大长细比交叉腹杆式塔式起重机的计算简图Fig.7 Calculation model of tower crane with large slenderness ratio and crossed flank rod

5 结论

格构式桁架结构如塔身、吊臂是塔式起重机及施工升降机等起重设备的主要组成部分，它们的稳定性关乎整机工作的安全性.桁架结构的稳定性分析由于其复杂性需借助有限元软件实现，通过对杆系结构稳定理论和有限元稳定理论的深入分析运用，解决了有限元软件分析超静定桁架结构稳定性出现误判的问题，完善了有限元软件在桁架结构稳定性分析中的应用，为工程应用提供了有益的参考和借鉴.

［1］全国起重机械标准化技术委员会.GB／T3811—2008 起重机设计规范［S］.北京：中国标准出版社，2008.National Standardization Technical Committee of Hoisting Machinery.GB／T3811—2008Design rules for cranes［S］.Beijing：China Standards Press，2008.

［2］夏拥军.计及二阶效应的柔性杆系动态分析及在起重机械中的应用［D］.哈尔滨：哈尔滨工业大学，2007.XIA Yongjun.Dynamic analysis with second-order effect for flexible beam systems and its application in crane［D］.Harbin：Harbin Institute of Technology，2007.

［3］李涵，陆念力.缀条式格构受压构件整体稳定性计算精度的探讨［J］.建筑机械化，2005（9）：25-28.LI Han，LU Nianli.Discussion about precision of whole stability of compressed sewed batten latticed column［J］.Construction Mechanization，2005（9）：25-28.

［4］陆念力，王佳，兰朋.格构式构件整体稳定性分析的等效惯性矩法［J］.建筑机械，2008（8）：79-82.LU Nianli，WANG Jia，LAN Peng.Equivalent inertia moment method to the overall stability analysis of lattice type beam［J］.Construction Machinery，2008（8）：79-82.

［5］陆念力，兰朋，李良.二阶理论条件下的梁杆系统精确有限元方程及应用［J］.哈尔滨建筑大学学报，1998，31（4）：67-74.LU Nianli，LAN Peng，LI Liang.Appilication of FEM of beam element with theory ofⅡ order［J］.Journal of Harbin University of Civil Engineering and Architecture，1998，31（4）：67-74.

［6］孙焕纯，王跃方.对桁架结构稳定分析经典理论的讨论［J］.计算力学学报，2005，22（3）：316-319.SUN Huanchun，WANG Yuefang.Comment on classical theory of stability analysis for truss structures［J］.Chinese Journal of Computational Mechanics，2005，22（3）：316-319.

［7］孙焕纯，王跃方，刘春良.扁桁架结构稳定分析几何非线性临界点——欧拉理论［J］.大连理工大学学报，2007，47（5）：629-633.SUN Huanchun，WANG Yuefang，LIU Chunliang.Geometrically nonlinear critical-point—Eulerian stability theory for stability analysis of shallow truss structures［J］.Journal of Dalian University of Technology，2007，47（5）：629-633.

［8］王勖成.有限单元法［M］.北京：清华大学出版社，2003.WANG Xucheng.Finite element method［M］.Beijing：Tsinghua University Press，2003.

［9］陈骥.钢结构稳定理论与设计［M］.第3版.北京：科学出版社，2003.CHEN Ji.Stability theory and design of steel construction［M］.3rd ed.Beijing：Science Press，2003.