基于Corsica的EAST等离子体平衡计算

程曹军， 肖炳甲， 刘成岳

(1.中国科学院等离子体物理研究所，安徽合肥 230031;2.合肥工业大学电子科学与应用物理学院，安徽合肥 230009)

托卡马克是当今世界上最有发展前景的核聚变实验装置，而在中国科学院等离子体物理研究所建成的EAST(Experimental Advanced Superconducting Tokamak)是世界上第1台全超导磁体托卡马克，具有非圆截面，实验目标是要实现长脉冲稳态运行以及在稳态运行条件下改善约束，从而为未来先进聚变反应堆奠定工程技术和物理基础。本文使用Corsica程序对EAST纯欧姆放电中的平衡位形建立进行了模拟，给出重要等离子体的参数剖面信息，如等离子体电流密度、温度分布等剖面。在建立平衡位形基础上开展了放电模拟研究，给出脉冲放电中电流和等离子体位置的演化结果。

1 物理模型

Corsica是一个二维平衡结合一维输运的1.5维平衡演化程序，用于托卡马克等离子体演变和诊断的模拟，是由美国LLNL(Law rence Livermore National Laboratory)开发的，被引入到中国科学院等离子体物理研究所。目前该程序已在世界各大型装置上广泛应用，如美国D3D装置上利用它做PF线圈的设计和中心和边界输运的耦合计算;在SSPX Spheromak上，利用它作为模拟工具研究该装置的平衡和稳定性;在ITER上利用它做装置的概念设计及放电模拟。Corsica在等离子体平衡位形建立、等离子体垂直位移控制、输运计算等方面都有广泛的应用[1-5]。

1.1 磁场结构及等离子体平衡方程

在环对称托卡马克系统中，磁场通常表示为:

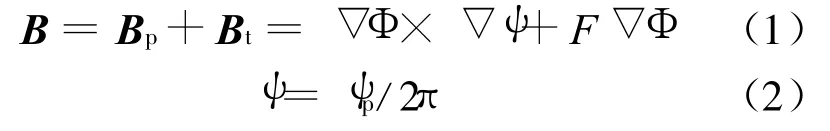
环对称托卡马克磁场结构示意图如图1所示。图1和(1)式、(2)式中，I p为等离子体电流;B t为环向磁场;Bp为极向磁场;Φ为环向角;θ为极向角; ψ为单位弧度内的极向磁通;ψp为总的极向磁通，定义为极向磁场的面积分，即ψp=∫B p◦d S。

电流通量函数F(current flux function)为等离子体极向电流，定义为电流密度的面积分，即

对于环对称托卡马克等离子体平衡位形而言，等离子体满足Grad-Shafranov方程[6]，即

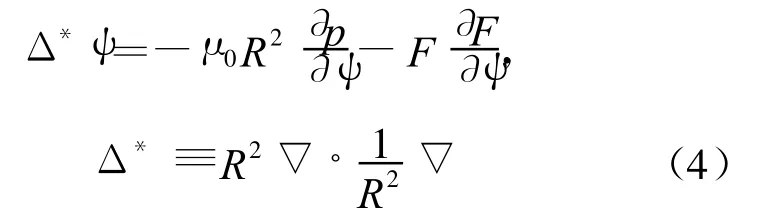
其中，Δ*为椭圆微分算符;R为等离子体径向R坐标。

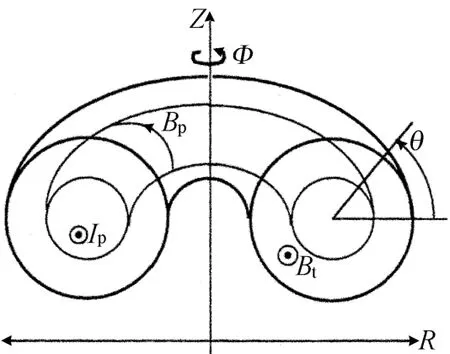
图1 环对称托卡马克磁场结构示意图

1.2 自由边界下的等离子体平衡算法

为了获得等离子体平衡位形及其等离子体剖面信息，在求解自由边界下的G rad-Shafranov方程时，需要等离子体压强p和安全因子q的分布信息。求解平衡方程后的输出结果为等离子体电流Ip、等离子体总的环向磁通 Φedge、等离子体磁场B及由此所获取的等离子体电流密度等剖面信息[7]。外部线圈上的电流Ii是通过一系列的电路方程求解的，该电路方程可以表示为:

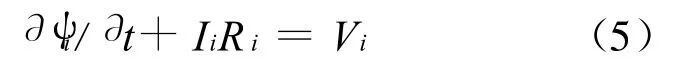
其中，ψi、Ii、Ri及Vi分别为第i个线圈上的磁通、线圈电流、线圈电阻及线圈上需要的电压，ψi=L ij Ij。其中，L ij为互感矩阵，是包含线圈和等离子体电流的复杂非线性函数。由于线圈上的磁通是已知的，所需要的线圈电流可通过以下迭代计算得到，迭代算式为:

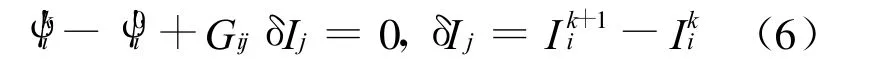
其中，k为迭代数;Gij为线圈的格林函数;为所需磁通值(输入)。

2 模拟结果及实验比较

2.1 EAST装置基本物理参数

EAST装置极向场系统采用14个超导磁体相对于装置的赤道面对称布置，如图2所示。

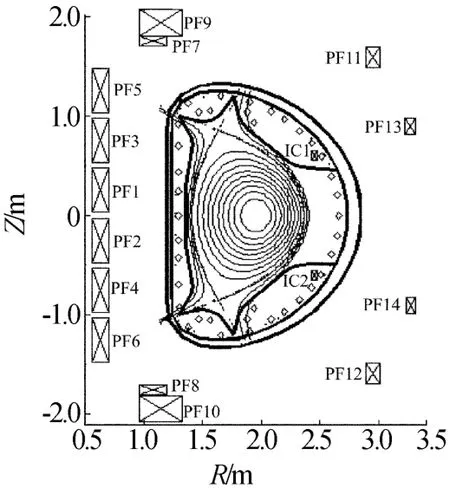
图2 EAST极向场线圈分布和截面示意图

PF1～PF6组成中心螺线管，其主要功能是提供实验中等离子体击穿、爬升及平顶所需的伏秒消耗，通常又称为欧姆场线圈。PF7和PF9主要用于等离子体的拉长，用于获得高性能参数的等离子体。PF11和PF13主要提供垂直场，用于等离子体的平衡，抵抗等离子体内部向外的扩张力，又称为平衡场线圈。详细的EAST极向场线圈参数和装置物理参数见文献[8，9]。

2.2 模拟结果及实验分析

在以上物理模型建立的基础上，具体分析了EAST实验中脉冲shot#8815炮放电中的等离子体平衡建立及放电模拟。以时间片t=1.8 s为例进行说明，将该时间片的等离子体压力和安全因子的剖面信息输入到等离子体平衡方程进行求解，如图3所示。

通过求解电路方程获得的外部极向场线圈中的电流与实验值的比较如图4所示。由图4可以看出，实验中线圈电流与模拟所得计算结果吻合较好。同时，该时间片在极向面(R，Z)内的等离子体平衡位形如图5所示，表明在该时刻等离子体成形稳定，形成拉长位形，为后续进行大拉长高参数放电奠定基础。等离子体电子密度、离子密度、电子温度及离子温度沿等离子体径向的剖面信息如图6、图7所示。

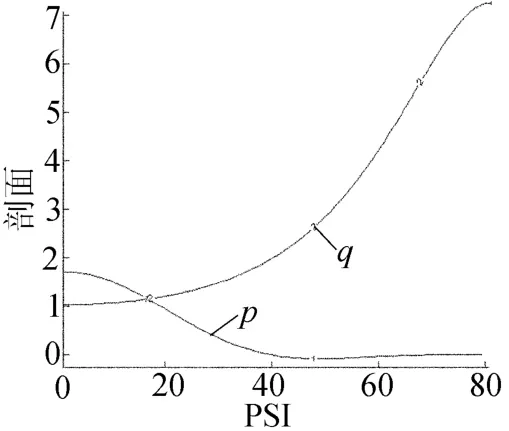
图3 等离子体压强p和安全因子q剖面

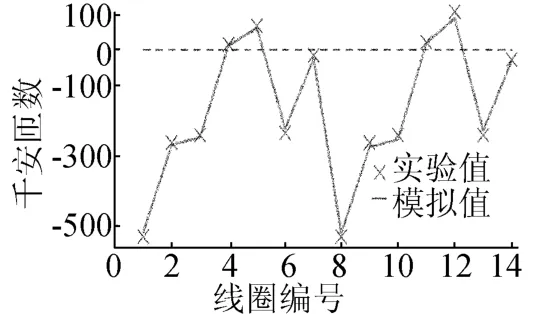
图4 PF线圈电流

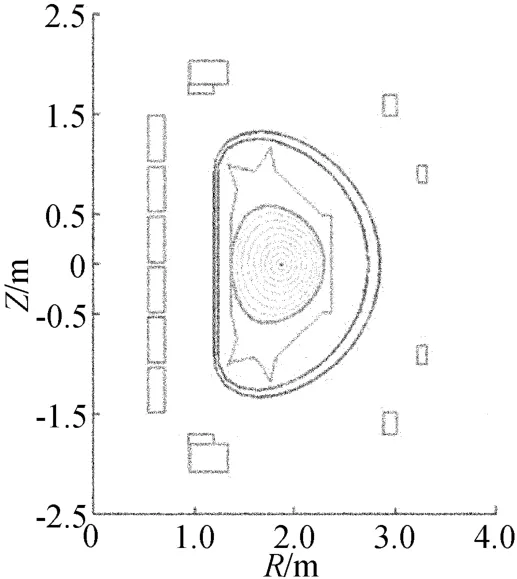
图5 等离子体的平衡位形

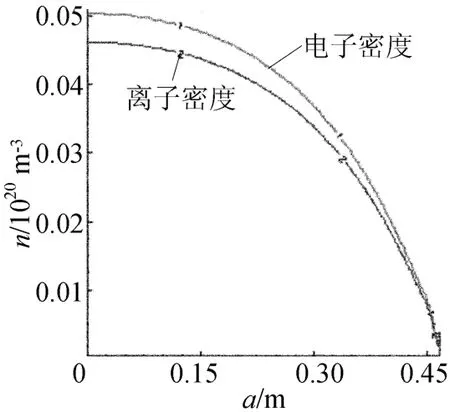
图6 电子密度和离子密度的剖面分布

由于芯部等离子体压力大，中心区的密度、温度都比边缘等离子体区的数值大，基本满足抛物函数分布。由于电子质量小于离子质量，电子的温度要高于离子温度。目前，等离子体的这些剖面分布在实验中还没有诊断信息，所以这些模拟预测的结果将对理解等离子体内部的物理过程和机理具有重要意义。

等离子体电流密度的剖面分布如图8所示，从图8可以看出，等离子体电流主要分布在等离子体芯部，在芯部峰化。同时，在以上平衡位形获得的基础上，开展了等离子体放电模拟的初步研究。

图7 电子温度和离子温度的剖面分布

图8 等离子体电流剖面分布

放电中等离子体电流、大半径及小半径随时间的演化如图9所示。

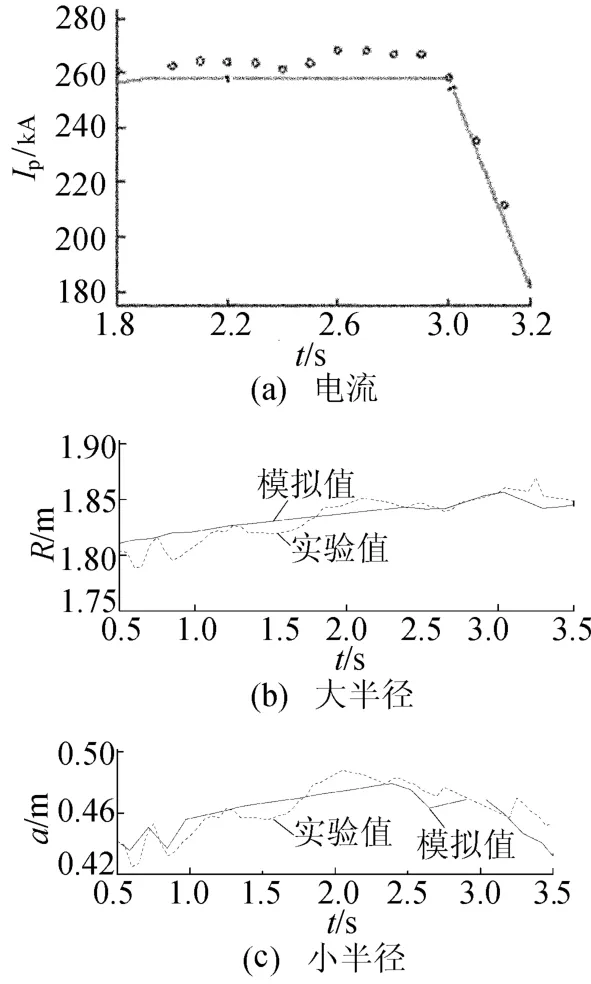
图9 等离子体电流、大半径、小半径随时间的演化

由图9a可看出，在t=1.8～3.0 s时，脉冲电流维持在260 kA的平顶，此后经历电流下降段，直至放电结束。整个过程模拟得到的等离子体电流I p与实验结果吻合较好。由图9b、9c可看出，模拟结果与实验吻合较好，这说明放电模拟过程中采用的EAST物理模型、等离子体电流和位置控制有很高的可靠性。

3 结束语

本文基于Corsica程序对EAST放电过程中等离子体平衡位形的建立进行了模拟，得到了预期的平衡结果，给出相应的等离子体电流、等离子体温度、等离子体密度等剖面信息，同时在建立平衡位形的基础上开展了等离子体的放电模拟研究。脉冲过程的等离子体电流、大半径及小半径的演化模拟结果与实验基本一致，说明了等离子体控制系统的合理性。这对于今后实验结果的分析和未来更深层次的EAST物理实验中等离子体平衡位形设计和控制都有重要的参考价值。

[1] Jardin SC，Pom phrey N，De Lucia J.Dynam icmodeling of transport and positional control of tokamaks[J].JCom put Phys，1986，66(2):481-507.

[2] Casper T A，Jayakumar J，Meyer W H，et al.ITER shape controller and transport simu lations[J].Fusion Engineering and Design，2008，83(2/3):552-556.

[3] Hum phrey s D A，Ferron JR，H yatt A W，et al.DIII-D integ rated plasm a con trol solutions for ITER and next-generation tokamaks[J].Fusion Engineering and Design，2008，83 (2/3):193-197.

[4] M cElroy L.Corsica:in tegrate simu lations for magnetic fusion energy[J].Science&Technology Review，May，1998: 20-22.

[5] 刘成岳，陈美霞，宋逢泉.EAST托卡马克长位形演化的数值模拟[J].合肥工业大学学报:自然科学版，2010，33(5): 770-772，782.

[6] 罗正平.托卡马克中等离子体平衡计算[D].合肥:合肥工业大学理学院，2007.

[7] Jardin SC，Bell M G，Pom phrey N.TSC simu lation of ohmic discharges in TFTR[J].Nuc lear Fusion，1993，33(3): 371-382.

[8] 刘 磊.EAST垂直不稳定性及反馈控制数值模拟[D].合肥:中国科学院等离子体物理研究所，2008.

[9] 牛兴平.EAST位形形成及演化的数值模拟[D].合肥:中国科学院等离子体物理研究所，2006.