湛江软黏土的流变本构模型研究

2011-03-15何利军吴应红

合肥工业大学学报（自然科学版） 2011年4期

何利军，蔡羽，吴应红

(1.中国科学院武汉岩土力学研究所，湖北武汉 430071;2.中交第四航务工程勘察设计院有限公司，广东广州 510230;3.荆州海事局，湖北荆州 434000)

我国沿海地区分布有广泛的海积软黏土。随着道路建设的高速发展，需要对软黏土的力学性质进行深入研究，因此发展和完善湛江软黏土的变形及变形控制理论显得尤为重要，而解决这些问题的关键之一是建立恰当的力学本构关系模型[1-8]。工程实例表明，土具有弹性、塑性和流变性，与其它类型土相比，软黏土的流变变形更为显著，建立合理准确的流变模型是土力学研究的重要任务。本文以湛江软黏土为研究对象，通过分析常规三轴剪切蠕变试验数据，建立了湛江软黏土流变本构关系的理论模型和经验模型。

1 蠕变试验及结果

试验仪器为GDS应力路径三轴仪，采用分级加载，试验围压为0、0.1、0.2、0.4 MPa。当围压为0.05 MPa时，本文根据湛江软黏土的三轴剪切蠕变试验，可得出不同轴向偏应力时应变随时间的变化如图1所示。由图1可知，土样在加载瞬时均有一定量的弹性瞬时应变，其值随偏应力的增大而不变或略有下降;瞬时弹性应变后，蠕变呈衰减稳定，变形随时间增长而趋于稳定。当偏应力继续增大至破坏强度时，瞬时变形后历时较短，即进入加速蠕变阶段并发生破坏，且破坏前有较明显征兆，取破坏强度[9]为0.16MPa。

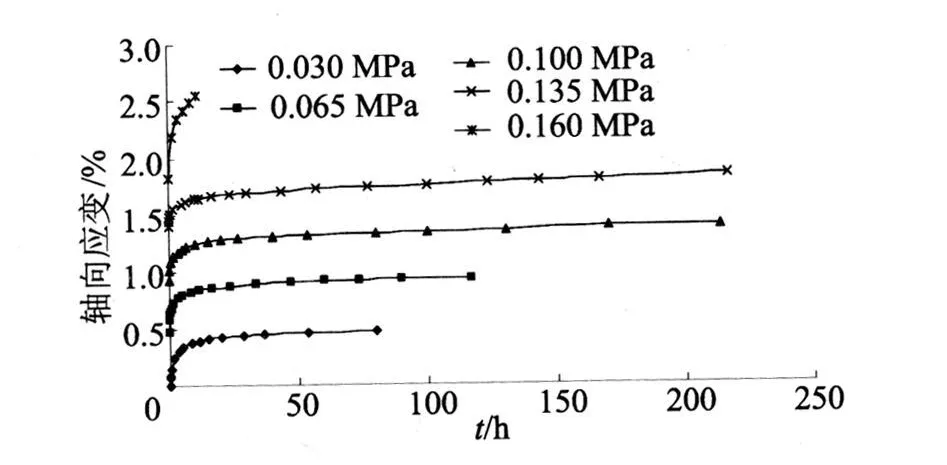
图1 蠕变试验曲线

若认为蠕变曲线主要由线性黏弹性变形和线性黏塑性变形构成，对于围压为0.05 MPa情况下的应力-应变等时曲线如图2所示，图2曲线可视为折线，折点约为0.028MPa，如果不考虑轴向偏应力为0.16 MPa的急剧破坏曲线，则线性黏弹性变形和线性黏塑性变形占主要部分。

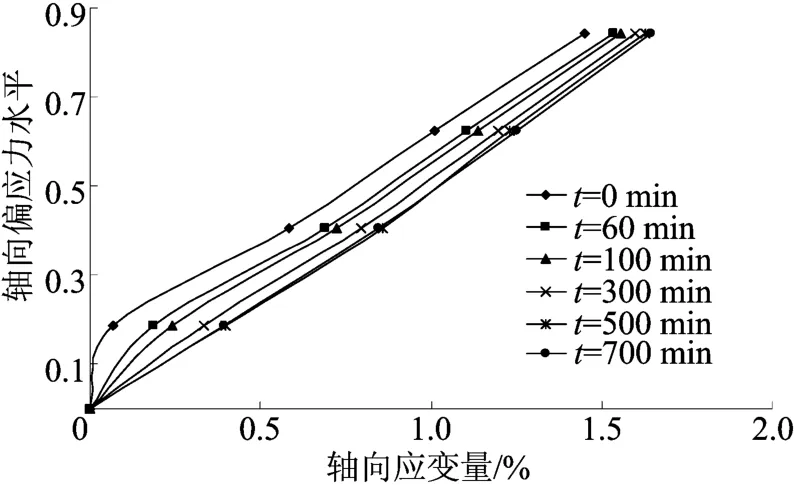
图2 应力-应变等时曲线

由以上分析可知，土的屈服应力 σs= 0.028MPa。建立模型时，线性黏弹性变形用广义Kelvin体描述，线性黏塑性变形用Bingham体或者用胡克体与黏壶串联的Bingham体来描述。同理，围压为0.1 M Pa时，σs=0.029 MPa;围压为0.2 MPa时，σs=0.05 MPa;围压为0.4 MPa时，σs=0.25 MPa。图2中的曲线为明显的折线形式，折点出现在第1级加载主应力差值之前，若不考虑该部分，可以发现图2近乎为直线，据此可以认为此围压下的蠕变变形曲线可以用线性黏弹性变形曲线来较好地逼近，即用广义Kelvin体描述。在其它围压下的情况基本相似。

2 湛江软黏土流变本构模型的建立

2.1 流变理论本构关系模型

线性黏弹性模型、西原模型、线性黏弹塑性模型，分别如图3～图5所示。

(1)五元件线性黏弹性模型如图3a所示。

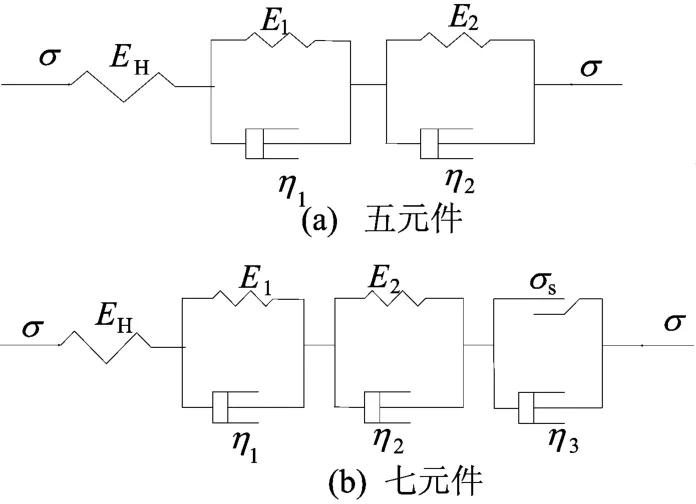
图3 线性黏弹性模型

其蠕变变形可表示为:

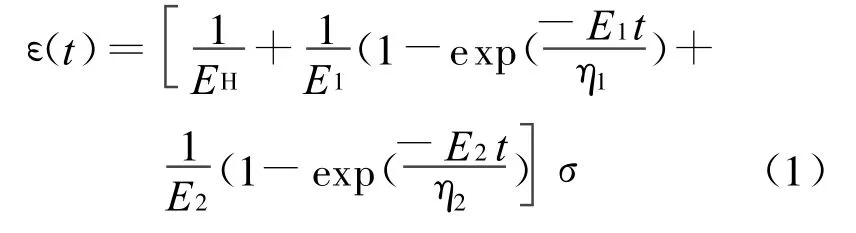
(2)五元件西原模型如图4a所示。

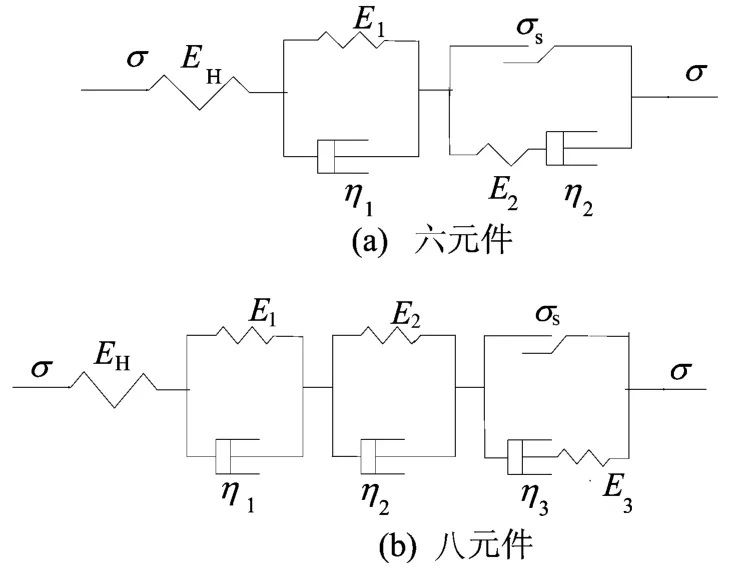
图4 西原模型

当σ≥σs时，蠕变变形可表示为:

(3)六元件线性黏弹塑性模型如图5a所示。

当σ≥σs时，蠕变变形可表示为:

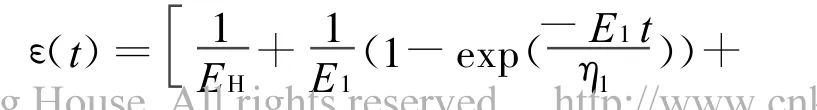
(4)七元件线性黏弹性模型如图3b所示。

其蠕变变形可表示为:

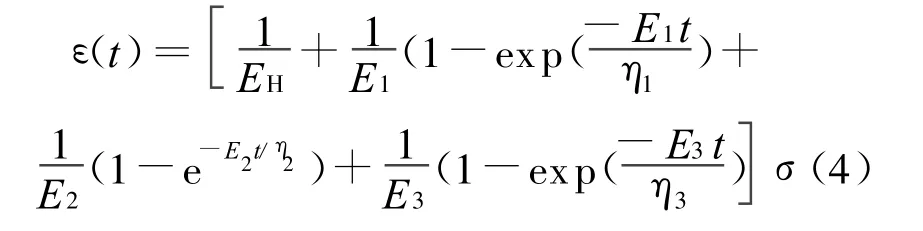
(5)七元件西原模型如图4b所示。当σ≥σs时，模型蠕变变形可表示为:

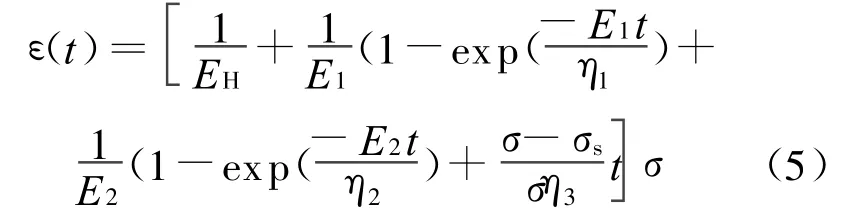
(6)八元件线性黏弹塑性模型如图5b所示。

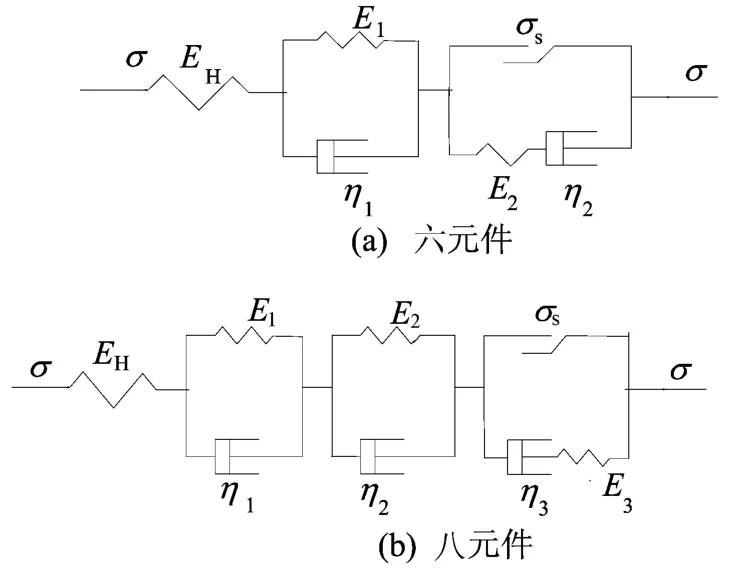
图5 线性黏弹塑性模型

当σ≥σs时，模型蠕变变形可表示为:

2.2 参数拟合与模型分析

模型建好后，对于各种理论模型由最小二乘原理按高斯-牛顿法进行曲线的非线性拟合[10]，本文应用M atlab程序进行计算机拟合，其拟合参数见表1～表6所列。

若用拟合的平均误差表示拟合精度，各模型的拟合平均误差见表7所列，从表7可以比较各模型的拟合精度。

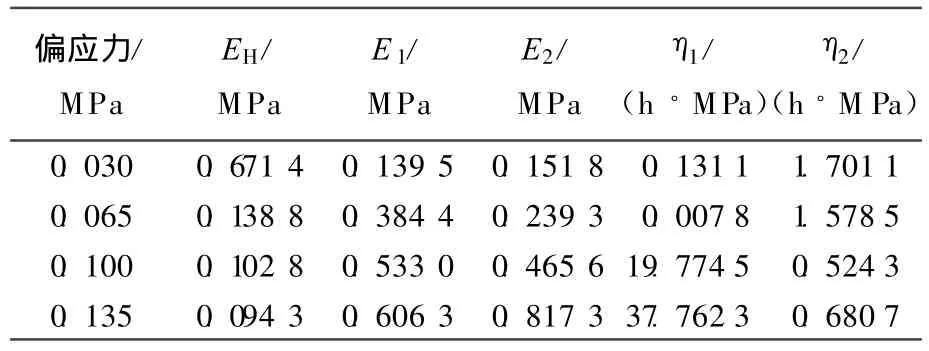
表1 围压0.05MPa时五元件线性黏弹性模型拟合参数

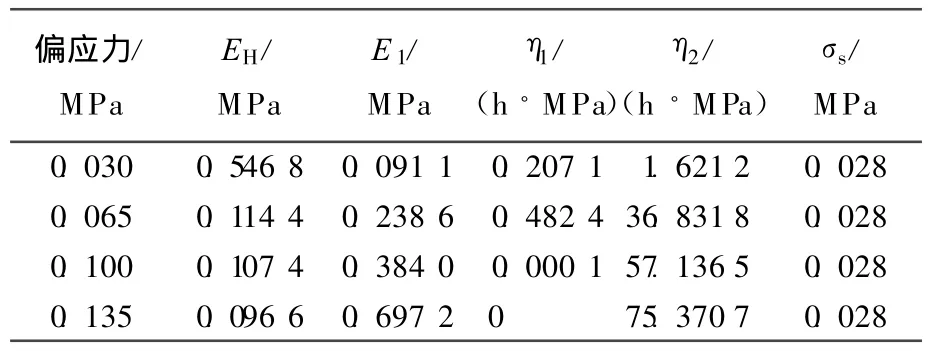
表2 围压0.05MPa时五元件西原模型拟合参数

表3 围压0.05 MPa时六元件线性黏弹塑性模型拟合参数

表4 围压0.05 MPa时七元件线性黏弹性模型拟合参数

表5 围压0.05 MPa时七元件西原模型拟合参数

表6 围压0.05 MPa时八元件线性黏弹塑性模型拟合参数

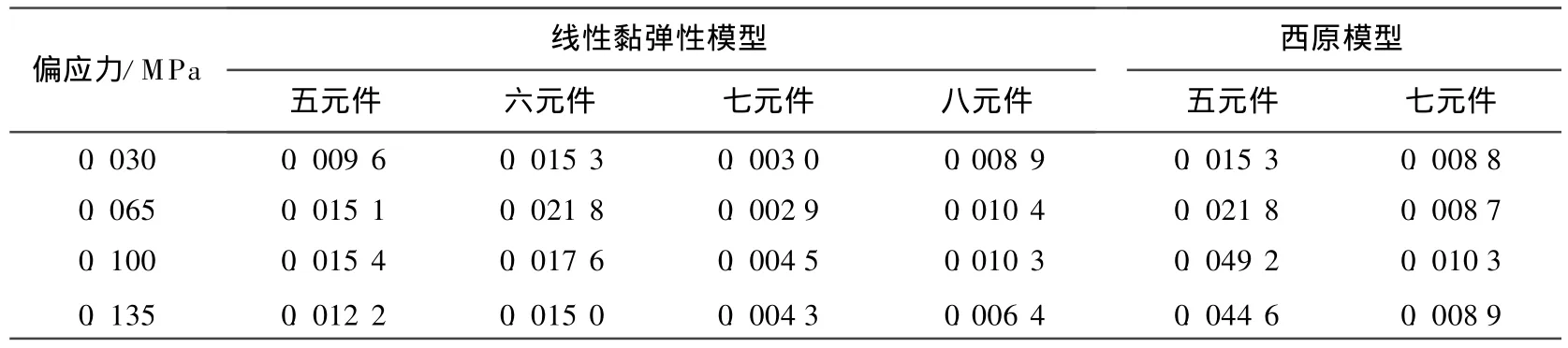
表7 围压0.05 MPa时各种模型拟合的平均误差

从表7可以看出，扩展的七元件线性黏弹性模型比五元件线性黏弹性模型的拟合精度要高，扩展的七元件西原模型比五元件西原模型拟合精度要高;扩展的八元件线性黏弹塑性模型比六元件线性黏弹塑性模型拟合精度要高。由此可看出，线性黏弹性模型的拟合精度最高，西原模型和线性黏弹塑性模型的拟合精度次之，这与蠕变变形中的线性黏塑性变形成份所占比例小、蠕变变形主要以线性黏弹性变形为主及七元件线性黏弹性模型曲线能更好地逼近蠕变曲线有关。

由表7还可以看出，线性黏弹塑性模型的拟合精度高于西原模型，这与线性黏弹塑性模型对线性黏塑性变形的描述能力高于西原模型有关。由于线性黏弹性模型的拟合精度已经很高，故建议有条件地选用五元件或七元件线性黏弹性模型来描述0.05 MPa围压下的湛江软黏土的蠕变变形。

2.3 不同围压下的拟合精度分析

除了进行围压为0.05 MPa的三轴剪切蠕变试验，还进行了围压为0.1、0.2、0.4 MPa的试验。围压为0.1MPa时，从0.03～0.295 MPa共分10级加载，围压为0.2 MPa时，从0.065～ 0.4 M Pa分5级加载，围压为0.4 M Pa时，从0.27～0.75 MPa分5级加载，广义Kelvin模型拟合的精度普遍较高，特别是在围压分别为0.05 MPa和0.4 MPa时，拟合精度略微降低出现在围压分别为0.1MPa和0.2MPa时，这是由于湛江软黏土的蠕变过程中，出现结构性损伤，从而导致产生非线性变形的因素增多，而当应力水平较低或出现高于结构屈服应力时，导致产生非线性变形的因素相对较少，而广义的Kelvin模型相对于西原模型和线性黏弹塑性模型，其描述非线性曲线的能力较弱。限于篇幅，本文不再一一列表详述。

2.4 湛江软黏土的理论本构模型

从以上分析可以看出，广义Kelvin模型描述湛江软黏土蠕变变形，反映了蠕变变形的最主要的特征，效果最好，西原模型和线性黏弹塑性模型能较全面地反映蠕变变形的变化规律，效果次之。若选择广义Kelvin模型描述湛江软黏土蠕变变形，可以通过运用最小二乘法原理得到0.1、0.2、 0.4 MPa围压下的拟合参数。

3 经验模型

3.1 经验型流变本构关系模型

(1)Singh-M itchell模型和 M esri模型。Singh-M itchell模型对应的蠕变变形可表示为:

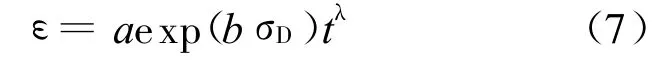
其中，σD为应力水平，20%≤σD≤80%;a、b、λ为拟合参数。

Mesri模型对应的蠕变变形可表示为:

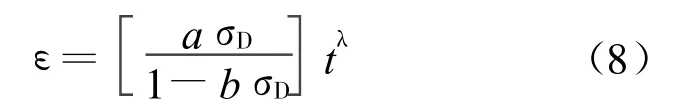
其中，σD、a、b、λ同(7)式。

(2)幂函数型经验本构模型。其蠕变变形可表示为:

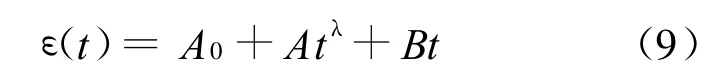
其中，A0为加载时的瞬时变形;λ为曲线走势的参数;B为亚稳定阶段蠕变速率。

3.2 参数拟合

同样运用最小二乘法原理，采用Matlab程序进行计算机拟合，其拟合参数见表8、表9所列。

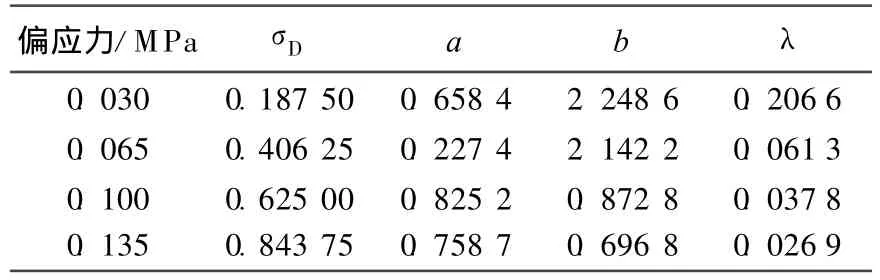
表8 围压0.05 MPa时Mesri模型拟合参数

表9 围压0.05MPa时幂函数型经验模型拟合参数

3.3 模型的分析与比较

拟合的平均误差见表10所列。

表10 围压0.05MPa时2种模型拟合平均误差的比较

由表10可以看出，幂函数型经验模型比Mesri模型的拟合精度高、使用更为简单，能够拟合的曲线形式更多，若选择幂函数型经验模型描述湛江软黏土蠕变变形，同样通过运用最小二乘法原理，可以得到0.1、0.2、0.4MPa围压下的拟合参数。

4 工程算例

工程算例取通过湛江软黏土地区的一条公路，路基宽度为30m，高度为6 m，地基土水平方向分析范围为基底宽度的2倍，竖直方向分析范围为地表18m，距离路面中心线10m范围内承受0.150MPa的法向应力。

求解思路是在 Visual studio 2005上以FLAC3D自带的Burger蠕变模型为蓝本，编写五元件线性黏弹性模型，然后嵌入FLAC3D，用FISH语言编写的线性插值程序可求出每个单元体在不同应力条件下的参数值，应用文献[9]的参数转换方法，将一维参数转化为三维参数后赋于每个单元体，模型中竖直方向的沉降量分布云图如图6所示。

以路基底部中心点为研究对象，除了利用五元件线性黏弹性模型求沉降外，利用文中的幂函数经验模型分别求出中心点以下的18个单元体的变形量之和，具体做法是根据每个单元体的应力场和表8～表10，利用线性插值决定每个单元体幂函数经验模型参数的取值，进而得到每个单元体竖直方向的变形量，认为18个单元体竖直方向的变形量之和为路基底部中心点的沉降量，用该方法计算时间与沉降量的关系如图7所示。