多点粘贴压电层合梁的数值模拟

曲 磊， 王建国， 丁根芳， 覃 艳

(合肥工业大学土木与水利工程学院，安徽合肥 230009)

0 引 言

压电层合结构作为传感器与致动器，在航天、精密控制与测量及微机电系统中广为采用[1，2]。压电层合结构已成为近20年来国内外学者研究的热点，近年来用于压电多层结构分析的有限元数值方法得到了飞速发展。

文献[3，4]最早开展了这方面的研究工作;文献[5]总结了压电三明治层合结构的有限元理论;文献[6]基于离散层理论提出了板壳的有限元分析模型;文献[7]提出了一种能用于拉伸致动与剪切致动3层压电耦合结构分析的通用有限元模型;文献[8]运用双线性四节点板单元研究了热压电层合板;文献[9]采用改进的Reissner-Mindlin模型用于压电层合板的有限元分析;文献[10，11]在压电有限元方面也做了很多工作;文献[12]基于一阶剪切变形理论，采用一种新的具有多自由度的四结点四边形有限单元CTMQE对压电复合板进行了研究;文献[13]基于状态空间法系统地研究了多层压电介质空间轴对称与非轴对称问题的解。

本文在文献[14，15]的基础上，建立了含有压电传感器与致动器的多层耦合结构的有限元方程，采用二维四结点四边形压电耦合单元，借助ANSYS/APDL语言，编制了适用任意组压电片通过面层材料粘贴于智能结构表面的力-电多场通用有限元分析程序(M PFEMP)。

本文首先运用该程序验算了叠层梁[16]，与文献[16]比较证明了方法的可行性与有效性;计算了由压电片、黏结层和主体材料组成的5层复合梁，算例中提供了1组压电片和2组压电片在不同边界条件下的计算结果;讨论了压电片长度和位置变化对梁的变形影响，还提供了闭环情况下前5阶自振频率和C-F情况下的振型图。

本文结论对智能结构的设计具有一定的参考价值，本文方法可以作为复杂不规则压电复合结构有限元分析的计算基础。

1 线弹性压电体有限元方程

压电层合结构作如下假定:①结构各层之间理想黏结;②遵循线性弹性压电体理论;③各个压电片之间无相互作用的电磁场干扰;④压电片上下表面完全覆盖电极。线性压电结构有限元方程[14]为:

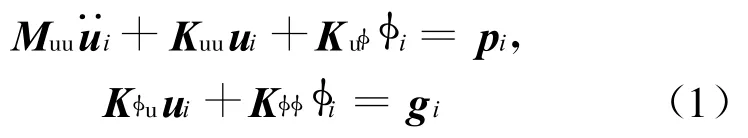
由方程(1)的第2式解出φi=Kφφ-1(g i-Kφu u i)，代入方程(1)的第1式可得:

方程(2)是以结点位移表示的线性压电结构的有限元法动力方程。

2 MPFEMP程序验算

力-电有限元分析程序(MPFEMP)主要采用参数化设计语言APDL，利用*DO、*ENDDO循环语句、*IF、*ELSE、*ENDIF等判断语句和*DIM矩阵定义语句来实现在压电片上模拟任意数量的电极，在任意电极上加载任意变化的电压载荷。为验证程序有效性，本文先对中间层全为压电层的叠层梁[16]展开对比验证分析。几何参数、材料常数、载荷和边界条件均同文献[16]，本文计算所得梁端挠度如图1所示。

由图1可看出，本文结果与文献[16]解析解(1.19E-7 m)吻合良好，误差率为1.3%，证明了本文计算方法的有效性。同时，本文的退化程序在文献[14]中也得到了验证。

图1 3层压电梁的变形曲线

3 n组压电片粘贴的5层压电梁

5层压电梁如图2所示，中间层主体材料为铝，黏粘层为刚性泡沫，压电层粘贴在黏粘面层上。压电材料极化方向平行于x轴。

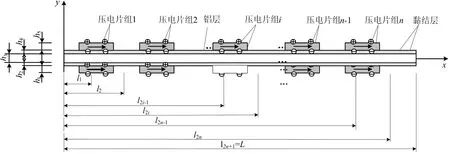
图2 5层压电耦合梁示意图

本文作如下假定:①电极相对于压电材料和铝层不计质量及刚度;②)压电层、电极、刚性泡沫和铝层的黏结是理想的，不存在相对位移;③压电材料不存在相互的电磁效应;④材料沿Z向变形均匀。梁总长L为100 mm，铝层h3为8 mm，黏粘面层为0.25mm，上下压电层等厚均为2mm，第i组压电片的长度ai和位置bi表达式为:

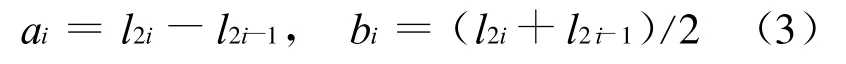
铝、刚性泡沫的材料参数见文献[7]，压电材料参数见文献[17]。在每个压电片上施加100 V电压荷载。分析中考虑梁两端固支(C-C)、两端均铰结(H-H)、一端固支一端自由(C-F)、一端固支一端铰结(C-H)4种边界条件。有限元分析采用四结点四边形单元(PLANE13)，5层梁结构划分成550个网格，兼顾了计算效率和计算精度。

3.1 粘贴1组压电片对梁的变形分析

压电片长度a=0.01m，位置b变化时，梁的变形情况如图3所示。

压电片位置b=0.05m，长度a变化时，梁的变形情况如图4所示。

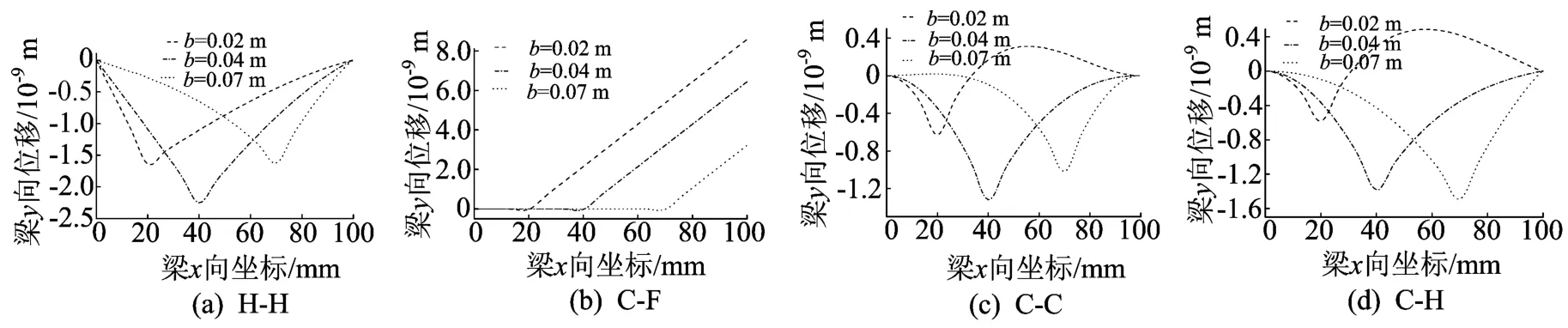
图3 压电片b变化时梁的变形情况

图4 压电片a变化时梁的变形情况

3.2 粘贴2组压电片对梁的变形分析

对于粘贴2组压电片对的梁，当压电片长度a1=a2=0.01 m，位置b1、b2变化时，梁的变形情况如图5所示。2组压电片的位置b1=0.025m，b2=0.075 m，长度a1、a2变化时，梁的变形情况如图6所示。

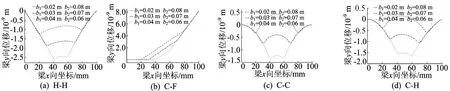
图5 压电片b1、b2变化时梁的变形情况

图6 压电片a1、a2变化时梁的变形情况

4 压电梁的自由振动

研究结构的自振频率与振型是结构形状控制和主动控制的基础。本文采用APDL语言编制层合梁的自由振动分析程序，压电单元采用二维四结点应力耦合单元，普通材料采用平面等参结构单元，计算:①单压电片对粘贴于结构表面的自由振动，a=0.01 m，b=0.05 m;②2组压电片对粘贴于结构表面的自由振动，a1=a2= 0.01 m，b1=0.025m，b2=0.075 m。材料参数同上，闭环前5阶自振频率见表1所列。

粘贴1组压电片对和粘贴2组压电片对悬臂梁的前3阶振型图如图7所示。

由图7可知，2种不同的粘贴方式，变形趋势基本相同，Benjeddou[7]的梁几何尺寸与本文不同，但是对比发现，梁整体的变形趋势基本相同。

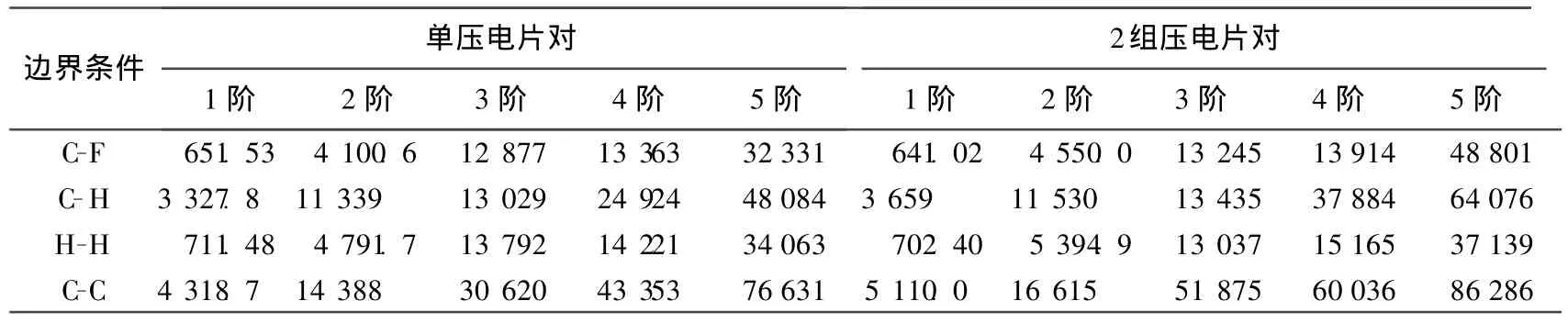
表1 单压电片对及2组压电片对黏结梁的前5阶自振频率 H z

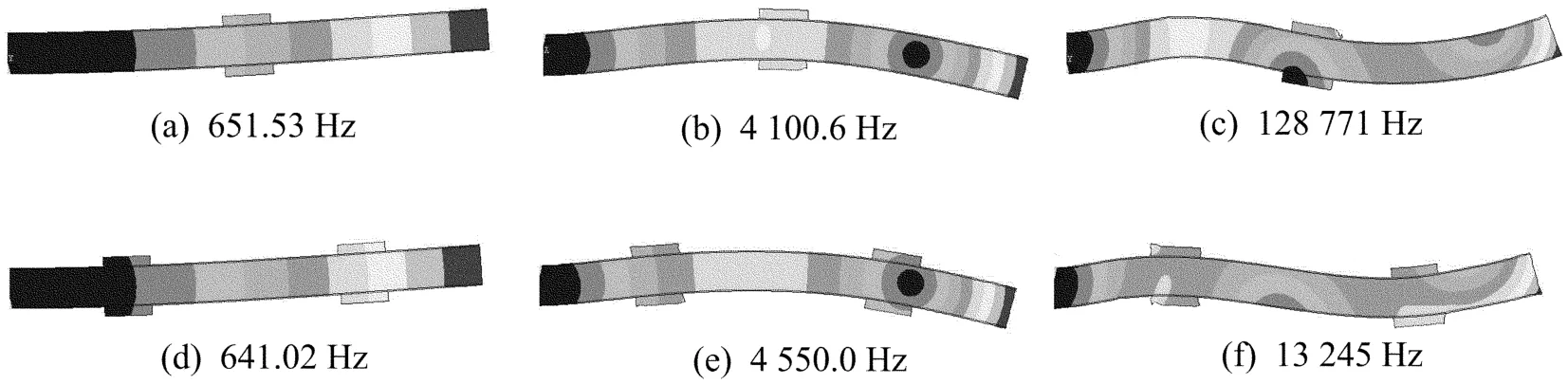
图7 单压电片对与2组压电片对粘贴梁的前3阶闭环振型图

5 结 论

本文利用APDL语言编制的有限元程序对表面粘贴压电片的层合梁进行了计算分析，考察了压电层位置和长度对梁变形的影响，分析了其自振频率和C-F情况下的振型图。结论如下:

(1)压电片相同的长度，不同的黏结位置和不同的边界条件，所产生的梁的最大位移值均不相同。H-H、C-H和C-C 3种情况下，梁的最大位移发生在压电片粘贴的中心处，随着压电片位置的变化，无论对于黏结1组压电片和2组压电片的梁，最大变形均受影响较大。所以，压电片在梁中的位置存在着一个最优值。同时在压电片长度固定的情况下，压电片位置的变化对于悬臂梁的最大变形影响不大。

(2)压电片长度越大，梁的最大位移越大。无论粘贴1组压电片还是2组压电片的层合梁，压电片长度增加，最大变形均增大，其中C-F情况下，最大位移发生在梁的自由端。而在其它的边界条件下，配置1组压电片的结构大部分发生在梁中间处;而配置了2组压电片的结构最终都在压电片所在的区域发生最大变形，形成非常有趣的双波峰现象。所以，利用多组压电片粘贴于结构表面，可以按照需要设计结构的变形。

(3)对比埋置1组压电片和埋置2组压电片的层合结构，发现压电片数量的增加对梁的最大位移影响不大，但是对于梁任何一处获得足够理想的致动效果影响较大。

(4)梁固支后自振频率明显增大。增加压电片的数量后，结构的自振频率略有增大，但是总体振型趋势变化不大，说明表面黏结形式的压电梁，压电片的数量和位置对梁的自由振动影响不大。

[1] Dem eis R B.Piezoelectric dam ping for space structures[J]. Aerospace AM，1985，23(9):32-33.

[2] Liao W H，W ang D H，H uang S L.W irelessmonitoring of cab le tension of cable-stayed b ridges using PVDF piezoelectric films[J].J Intel Mat Syst Str，2001，12(5):331-339.

[3] A llik H，Hughes T J.Finite element method for piezoelectric vib ration[J].Int J Num er Meth Eng，1970，2: 151-157.

[4] C raw ley E F，Deluis J.Use of piezoelectric actuators as elements of intelligent structu res[J].AIAA Journal，1987，25(10):1373-1385.

[5] H a K H.Finite-element analy sis of sandw ich plates:an overview[J].Compu t Struct，1990，37(4):397-403.

[6] Tzou H S，Ye R.Analysis of piezoelectric structu res with lam inated piezoelectric triangle shell elements[J].AA IA Journal，1996，34:110-115.

[7] Benjeddou A，Trindade M A，Ohayon R.A unified beam finite elem en tmodel for extension and shear piezoelectric actuationm echanisms[J].J Intel M at Sy st Str，1997，8(12): 1012-1025.

[8] Lee H J，Saravanos D A.Generalized finite element formulation for smart multilayered thermal piezoelectric composite plates[J].Int J Solids Structures，1997，34(26): 3355-3371.

[9] Carrera E.An improved Reissner-M indlin-type m odel for the electromechanical analysis of m ultilayered plates including piezo-layers[J].J Intel Mat Syst Str，1997，8(3): 232-248.

[10] Tian X G，Shen Y P.Finite element analysis of thermoelastic behavior of piezoelectric structuresunder finite deformation[J].Acta M ech Solida Sin，2002，15(4):312-322.

[11] 丁皓江，池毓蔚，国凤林，等.压电材料轴对称有限元分析[J].计算力学学报，2000，17(1):1-7.

[12] Cen Song，Soh A K，Long Y Q，et al.A new 4-node quad rilateral FE model w ith variable electrical deg ree of freedom for the analysis of piezoelectric lam inated composite p lates [J].Composite Stru ctures，2002，58(4):583-599.

[13] W ang JG，Fang SS，Chen L F.The state vector methods for space axisymmetric p rob lem s in multilayered piezoelectric media[J].Int J Solids Structu res，2002，39: 3959-3970.

[14] 丁根芳，王建国，覃 艳.自感知压电层合梁的数值分析与数值模拟[J].工程力学，2006，23(2):131-136.

[15] 王建国，覃 艳，丁根芳.单点配置压电层合结构的优化设计[J].合肥工业大学学报:自然科学版，2007，30(5): 594-597.

[16] Zhang X D，Sun C T.Formu lation of an adap tive sandw ich beam[J].Smart Mater Struct，1996，5(6):814-823.

[17] Sm its J G，Dalke S I，Coony T K.The constituent equationsof piezoelectric bim orphs[J].Sensor and Actuators A:Physical，1991，28:41-61.