新型TM模介质谐振器及其小型化应用
2011-03-15张忠祥吴先良
张忠祥, 陈 畅, 吴先良
(1.合肥师范学院物理与电子工程系,安徽合肥 230601;2.中国科学技术大学电子工程与信息科学系,安徽合肥 230041)
目前,个人移动通信和卫星通信系统飞速发展,对通信系统中的滤波器提出了高性能化和小型化的要求。随着微波介质陶瓷材料的性能和稳定性的不断提升,介质谐振器在微波系统中已获得越来越广泛的应用,例如滤波器、双工器和振荡器等。在移动通信系统中,金属同轴腔滤波器和介质滤波器都有广泛的应用,金属腔同轴谐振器和滤波器具有低成本、频率可调节范围宽和高次模远离主模等特点[1,2],而介质谐振器和滤波器具有高Q值、低损耗和温度稳定性高等特点[3-5]。
金属同轴腔谐振器的单腔无载Q值低于介质谐振器的主要原因,在于其内部谐振杆在谐振时其金属表面需要消耗附加损耗。鉴于横电模(TE)介质谐振器的电场和磁场的分布特点,TE模介质谐振器的单腔无载Q值要高于横磁模(TM)介质谐振器和金属同轴腔谐振器,但是其单腔外形尺寸要远远大于上述2种谐振器的单腔尺寸,所以TE模介质谐振器一般应用于对滤波器性能要求很高而对外形尺寸没有太高要求的场合。对于传统的TM模介质谐振器,其谐振器的上端面和下端面均金属化,短接于金属腔体的底部和上盖板,由于在腔体的底部与盖板间强电场的存在,引起金属表面损耗较大,即使采用的微波介质材料本身的损耗非常低,TM模介质谐振器的单腔无载Q值的提升也受到限制[6,7]。
本文给出了一种新型的TM模介质谐振器结构,只对其底部进行金属化处理,顶部端面开路与腔体的上盖板间形成一个空气间隙。该结构的TM模介质谐振器的单腔无载Q值要高于传统的TM模介质谐振器和金属同轴腔谐振器;同时其谐振腔外形尺寸要小于上述2种谐振器的谐振腔外形尺寸,与金属同轴腔谐振器结构相比,在水平面上可以节省约30%的产品外形尺寸。本文所提的新型TM模介质谐振器结构形式,可以对现代移动通信系统中的金属同轴腔滤波器和双工器进行完全或者部分的替代。本文最后给出了一个第3代宽带码分多址(WCDMA)通信系统中的8腔3传输零点的新型TM模介质滤波器设计实例,其测试结果与仿真结果吻合。
1 TM模介质谐振器
新型TM模介质谐振器的典型结构如图1所示,介质谐振器底部安装在一个矩形立方体或者圆柱体的谐振腔体内,且介质谐振器中间有一个内孔,用来对谐振频率进行一定范围内的调节。介质谐振器的外形可以为圆柱、矩形柱,或者横截面为便于机加工与模具处理的各种图形。为了提高谐振器的单腔无载Q值和减小谐振器的外形尺寸,本文选择介电常数为45的微波介质陶瓷材料,其材料的Q f=45 000。
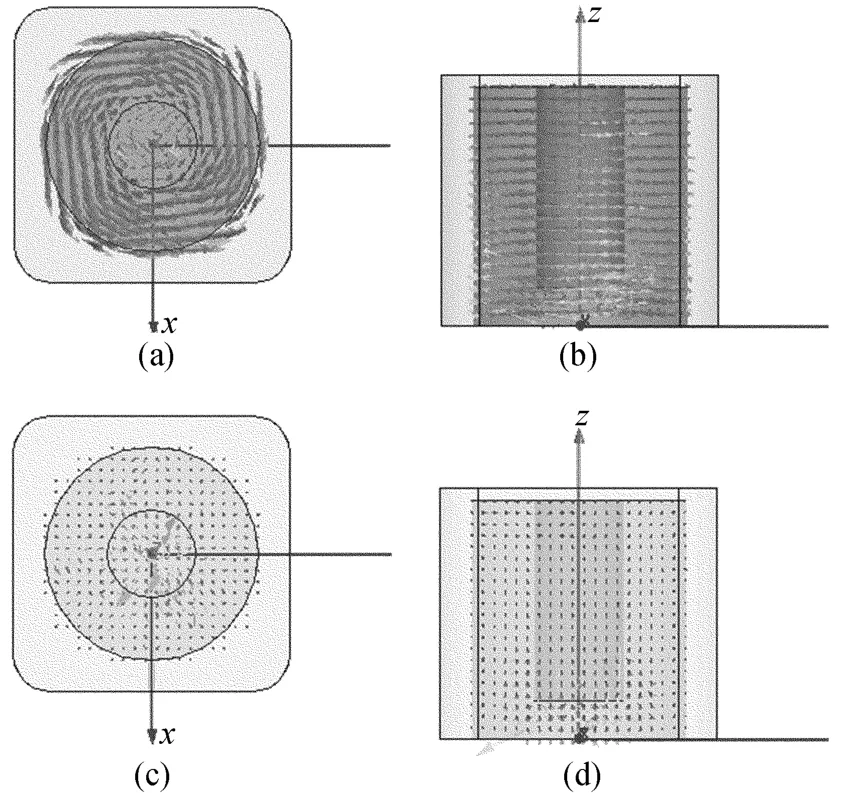
图1 新型TM模介质谐振器结构和场强分布示意图
同时,图1给出了新型TM介质谐振器的电场和磁场的分布示意图。
图1a为谐振器的磁场分布情况,图1c为谐振器的电场分布情况。
在图1中可以看出,其磁场只分布在水平面内,环绕着介质谐振器形成一个封闭的圆环;而电场则垂直于水平面,从上往下形成近似直线的分布。由图1所示场强分布情况,可以看出该谐振器工作在TM模式,是一种新型TM模介质谐振器。
以第3代WCDMA移动系统中下行频带中心频率2 140MHz的单腔谐振器为例,表1给出了金属同轴腔谐振器和新型TM模介质谐振器的腔体结构参数和谐振频率与单腔无载Q值的计算结果,由于在设计中没有考虑频率调节部件的影响,所以一般选择其谐振频率要高于目标频率。从表1可以看出2种谐振器在其谐振频率基本一致和单腔无载Q值不低于金属同轴腔的前提下,TM模介质谐振器的水平面单腔尺寸只有传统金属同轴腔外形尺寸的70%左右,可以很好地应用于对腔体外形尺寸有小型化需求的情况。

表1 金属同轴腔与TM介质谐振腔相关参数对比
在基于选择的介电常数为45的微波介质陶瓷材料的基础上,图2给出了表1中所示的TM模介质谐振器的单腔测试曲线,其测试结果谐振频率在2.341 4 GH z,3 dB带宽为664.843 kH z,通带损耗S21为-22.015 dB,单腔无载Q值为3 536,与表1所列的仿真计算结果相吻合。

图2 TM模介质谐振器单腔测试曲线
2 滤波器小型化应用
作为TM模介质谐振器的小型化设计应用,本文给出了一个WCDMA移动系统中工作带宽为2 110~2 170 MH z的8腔3传输零点的广义切比雪夫模型的带通滤波器设计实例。耦合矩阵为(1)式所示[8-10],矩阵中对角线上数值为滤波器相应单腔的谐振频率,非对角线上数值为相应腔体间的耦合系数。TM介质谐振器的单腔腔体外形尺寸为22 mm×22 mm×20 mm。

为提高TM模介质谐振的带外抑制特性,在TM模介质滤波器的输入腔和输出腔采用传统的金属同轴腔结构,该TM模介质滤波器结构示意图如图3所示。
在图3中,正耦合系数分别通过级联腔体间的窗口和非级联交叉腔体间的盖板上的短路探针来实现,谐振器频率的精细调节通过盖板上的调谐螺杆来进行。
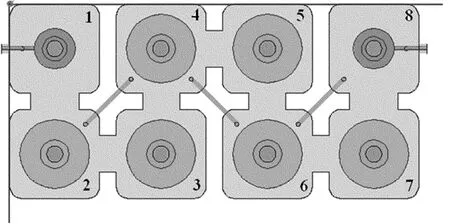
图3 8腔3传输零点TM模介质滤波器结构示意图
利用全波电磁场仿真软件ANSOFT-HFSS,对图3所示TM模介质滤波器的谐振器尺寸、耦合窗口宽度以及短路探针的长度等参数进行初值计算,利用ANSOFT-HFSS和ANSOFT-Designer相结合进行协同优化仿真,对参数进行优化调节以满足产品的性能指标要求。
优化响应曲线如图4所示,在工作频带2 110~2 170MHz,其输入与输出端口回波损耗小于-20 dB或者端口驻波比VSWR小于1.2,插入损耗在频率2 170 MHz处小于-1.35 dB,在频率2 110 MHz处-0.8 dB,在频率高于2 190 MH z处带外抑制大于-90 dB。
图5所示为新型TM模介质滤波器的实物照片,在保持性能指标不变的前提下,其产品的外形尺寸较传统金属同轴腔滤波器在水平面上节省了大约30%,为移动通信系统中腔体滤波器的小型化设计提供了一种新的方法。
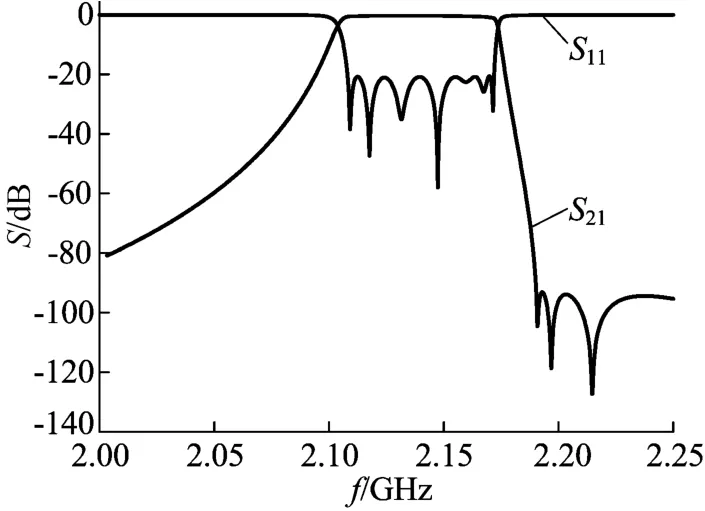
图4 介质滤波器优化响应曲线

图5 TM模介质滤波器实物照片
从图5中可以看出,介质谐振器下端安装在滤波器的腔体底部,输入和输出腔体采用了传统的金属同轴腔谐振器结构,3个传输零点的位置在2-4腔体、4-6腔体和6-8腔体间分别实现。
TM模介值滤波器测试曲线如图6所示,其通带2 110~2 170 MH z内端口驻波比VSWR小于1.2,插入损耗在频率2 170 MHz处,小于-1.41 dB,在频 率 2 110 MHz处小于-0.85 dB,在高于2 190 MH z处带外抑制大于-90 dB。考虑到接插件的连接损耗,其测试结果与仿真结果非常吻合,证明了设计方法和模型仿真优化的正确性。
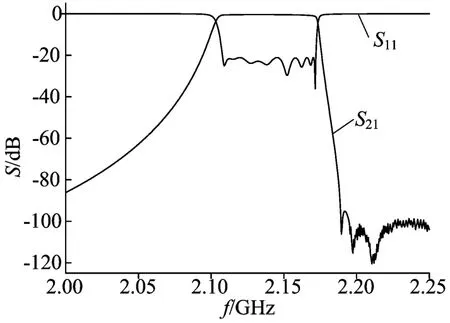
图6 TM模介质滤波器测试曲线
3 结束语
本文给出了一种新型TM模介质谐振器和介质滤波器,该介质谐振器下端安装在滤波器腔体的底部,上端与滤波器的腔体盖板间有一个空气间隙,在更小的腔体内以获得较传统TM模介质谐振器更高的单腔无载Q值;同时给出了该结构介质谐振器的场强分布图,以及单腔特性参数的仿真计算。最后,本文给出了一个8腔3传输零点的TM模介质滤波器设计实例,外形尺寸较传统金属同轴腔滤波器在水平面上节省约30%。其测试结果与仿真结果吻合,证明了该方法的正确性和可行性,为移动通信系统中滤波器的小型化应用提供了一种可行的途径。
[1] Matthaei G L.Comb-line band-pass filter of narrow orm oderate bandw idth[J].M icrow ave Journal,1963,6(8): 82-91.
[2] Kudisa C,Cameron R,Tang W.Innovations in microwave filters andm ultiplexing netw orks for comm unication satellite system s[J].IEEE T ransactions on M icrow ave Theory and Techniques,1992,40(6):1133-1149.
[3] Moraes M O,Borges F R.Efficien t technique for suppression of undesirab le m odes in dielectric resonator filters [C]//IEEE M TT-S International M icrow ave&Optoelectronics Conference,2009:775-777.
[4] Fiedziuszko S J,Hunter IC,Itoh T,et al.Dielectricmaterials,devices and circuits[J].IEEE Transactions on M icrowave Theory and Techniques,2002,50(3):706-720.
[5] Shen Tao,Kaw thar A Z,Wang Chi.Tunable dielectric resonators with dielectric tuning disks[J].IEEE T ransactions on M icrow ave Theory and Techniques,2000,48(12):2439 -2445.
[6] M ichaelH.Bandpass filter using TM-mode dielectric rod resonators w ith novel input coupling[C]//IEEE-IMS,2009: 1601-1604.
[7] H oft M.Y-shape dielectric dual-m ode resonator[J].IEEE Transactions on M icrow ave Theory and Techniques,2008,56(12):2519-2525.
[8] Wang C,Zaki K A.Dielectric resonators and filters[J]. IEEEM icrow ave Magazine,2007,56(10):115-127.
[9] Kabir H,W ang Y,Yu M,et al.Efficient neu ral netwo rk techniques for applications in m icrowave filter design[J]. IEEE Transactions on M icrowave Theo ry and Techniques,2007,56(12):1156-1167.
[10] 杨 梅,陈明生,吴先良,等.基于最佳一致逼近的高阶矩量法及其应用[J].合肥工业大学学报:自然科学版,2010,33(4):593-596.
