异方差条件下两种回归方法的比较

张敏强,王宣承

（1.华南师范大学 心理应用研究中心，广州 510631；2.上海财经大学 统计与管理学院，上海 200433）

1 最小二乘回归与分位数回归

在现有的心理统计模型中，最小二乘回归（Ordinary Least-Square Regression，简称OLSR）模型是一种最常用的统计分析技术，它主要用于研究一个因变量与多个自变量之间的相关关系。例如某产品的销售量与价格，考生的学业成绩与地域、性别和智商之间的关系等等。最小二乘回归模型利用观测数据来拟合因变量与各个自变量之间的函数关系式，分析这些影响变量之间的作用程度，进而对相关变量进行估计、预测和控制。

最小二乘回归模型具有其显而易见的优点，包括：意义直观，便于理解；计算简明，其优越性在前计算机时代无可比拟；以条件均值为目标函数，具有精密完整的数学形式等。

设多元回归模型为：

将所有的自变量用矩阵X表示，可以得到：

对（2）式求解，需要求出使残差的最小二乘方之和最小化的β估计值，即需要满足：

其一阶导数为：

Markov于1900年证明了Gauss-Markov定理：若观测样本满足最小二乘回归模型的基本假定，则在所有的无偏估计量中，最小二乘估计量是最优线性无偏估计量（Best Linear Unbiased Estimator，简称BLUE）。即若满足回归模型的假设条件，可以证明，最小二乘估计量具有如下性质：

（3）有效性。在所有线性无偏估计量中，最小二乘估计量β＾的方差最小。其最小方差为：

尽管最小二乘回归具有易于理解的优点和BLUE等优良的统计特性，但是最小二乘法的假设比较严格，随机误差项需要满足零均值、同方差、无自相关、与自变量之间不相关、正态分布等条件，一般条件下这些假设难以全部满足。此时就可能产生异方差、自相关等问题，从而影响回归系数估计的准确性和有效性。

由于OLSR的条件假设比较严格，且只能求出关于因变量条件分布上平均水平的描述，对于条件分布上其他水平的细节信息无法测算。Koenker和 Bassett（1978）提出了基于gh分布的分位数回归方法（quantile regression，简称QR），它对于残差的分布没有特定的要求，因而比OLSR具有更大的适用性；它可以根据不同的分位点来构建回归方程，从而在不同的因变量条件分布上，提供更加细致全面的关于的各局部信息。

设xi(i=1,2,…n)是一个K×1阶矩阵，则QR方程可以表示为：

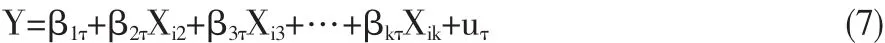
或以矩阵形式表示为：

分位数回归通过设定不同的分位点，来代表因变量的不同水平，在（1.8）式中用表示。当τ=0.5时，由于是在中位数水平上构建回归方程，此时的分位数回归也叫中位数回归（Median Regression,简称MR）。

2 异方差

最小二乘回归模型的一个重要假设是进入总体回归方程的随机误差项ui同方差，即Var(uj)=E(uj2)=σ2。若方差随观测值不同而发生变化，即Var(uj)=σj2，这就是异方差情况。图1描述了回归模型存在同方差和异方差时的不同情况。

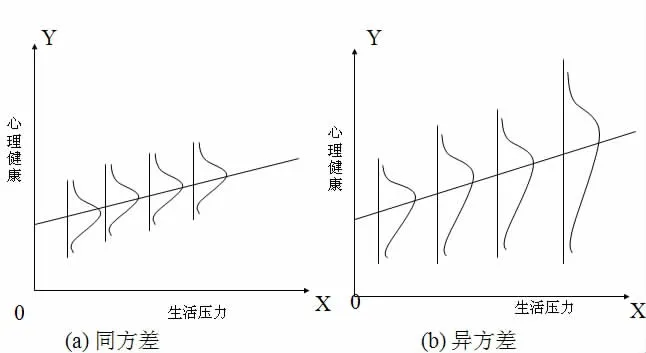
图1 同方差和异方差直观图

产生异方差的原因很多。如果回归模型构建得不合适，测量误差和模型中被忽略的一些因素对因变量发生了影响，即潜在的自变量被纳入到随机误差项中，导致误差变异随着自变量的变化而变化，可能产生异方差；如果来自不同抽样单元的因变量观测值存在较大差异，也可能产生异方差。异方差问题多存在于截面数据中而非时间序列数据中，如在社会调查中研究者经常采用大规模问卷施测的方式收集数据，被试的单位可能具有不同的规模，如大公司、中等公司和小公司，由规模效应导致方差随着自变量变化而波动。因此异方差在心理研究中应具有重要的研究和使用价值。

异方差的存在对OLSR模型的影响表现在：

（1）最小二乘估计量仍然是线性无偏的，但不再具有有效性（最小方差性）。

当异方差发生时，式（5）依然成立，但是公式(6)需调整为：

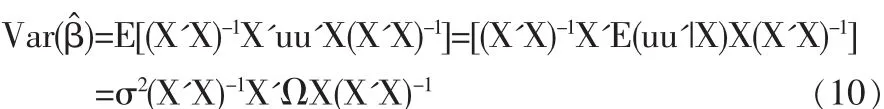
其中

这里Ω是一个正定矩阵且Ω≠I。

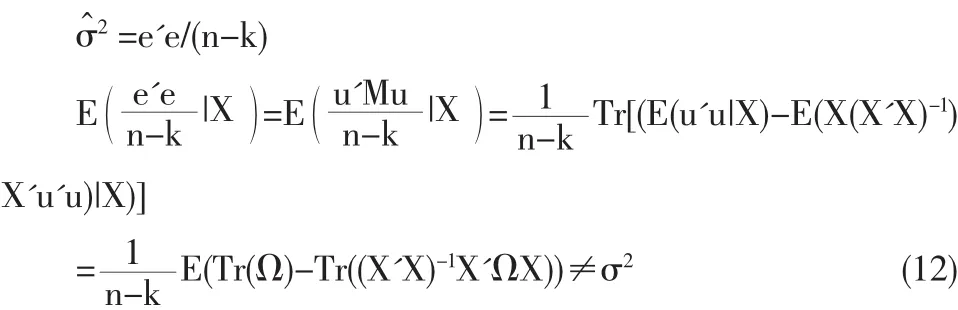
（3）建立在t分布和F分布上的置信区间和假设检验是不可靠的，如果沿用OLSR的检验方法，很可能导致错误的结论。

由此可见，当随机误差分布出现异方差情况时，OLSR不再是最优线性无偏估计量，而且会产生误差方差和参数检验的有偏估计，对于研究者来说统计方法上这样的偏差是无疑致命的，它将直接影响到结论的稳定性和可靠性。此时的样本观测值并未在因变量条件分布的平均水平周围呈现规则的分布，而是离散于条件分布的各水平中。若使用QR模型，就有可能将各水平上的回归效应分离出来，克服OLSR的缺陷。以下将用模拟数据和实测数据加以验证。

3 异方差条件下两种回归方法的比较

3.1 模拟研究

模拟生成一批数据集，包含自变量X，因变量Y和残差项e，共有500个观测样本。其中自变量从0到5均匀分布的区间内抽取，残差项e=z*(X+1)，z～N(0,1)。即残差项与自变量存在着同向相关关系。因变量Y的值可通过关系式Y=3X+e求出。

图2 异方差X-散点图

表1 异方差条件下QR和OLSR的系数比较

对这批异方差数据同时进行OLSR与QR对比分析，其结果如表1。

利用OLSR估计出来的结果是：

其中，回归系数β1差异显著（p＜0.01），R2=0.61。

在QR模型中，我们仍然选取5个分位点：0.1、0.25、0.5、0.75、0.9，从而可以得到一组方程：

对比OLSR和MR，二者的回归系数估计值几乎相等，两条回归线在图3中已经重叠在一起。异方差对于OLSR的影响在于其参数估计的有效性，并不影响参数估计的线性无偏性，当模拟条件控制较好时，OLSR的参数估计仍然是准确的，它和MR都代表了条件分布的中等水平，只是一个是以均值的角度来度量、而另一个是以中位数来度量。

对比不同分位点上的QR方程，由表1所示：自变量X的回归系数随着的增大而依次递增，变化的范围从1.88到4.22，全距为2.34。在0.1的分位数水平上，每增加1个单位的X，Y增加1.88个单位；而在0.9的高分位数水平上，每增加一个单位X，就可以增加4.22个单位的Y。说明自变量X对于因变量Y的解释作用随着因变量水平的增加逐渐增强，在图3中表现为5条QR曲线的倾斜越来越陡。

对比QR和OLSR随着分位点变动的情况，OLSR的回归系数及其置信区间依旧在各个分位点上保持恒定，但是QR的回归系数随着的增加而依次递增。在低分位点处，即在因变量Y的低水平上，QR的回归系数普遍小于OLSR的；在高分位点处，即在因变量Y的高水平上，QR的回归系数普遍大于OLSR的。而且在高低分位点处，QR的回归系数估计值都在OLSR回归系数的置信区间以外，说明此时两种方法求出的回归系数具有显著差异。

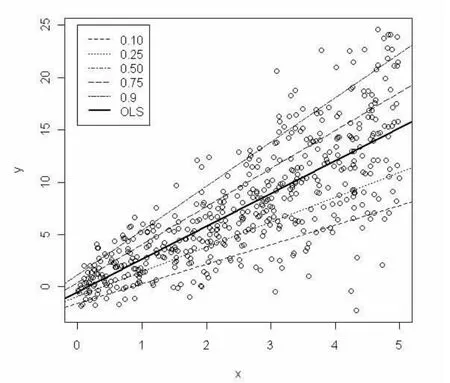
图3 异方差下的OLSR曲线和QR曲线

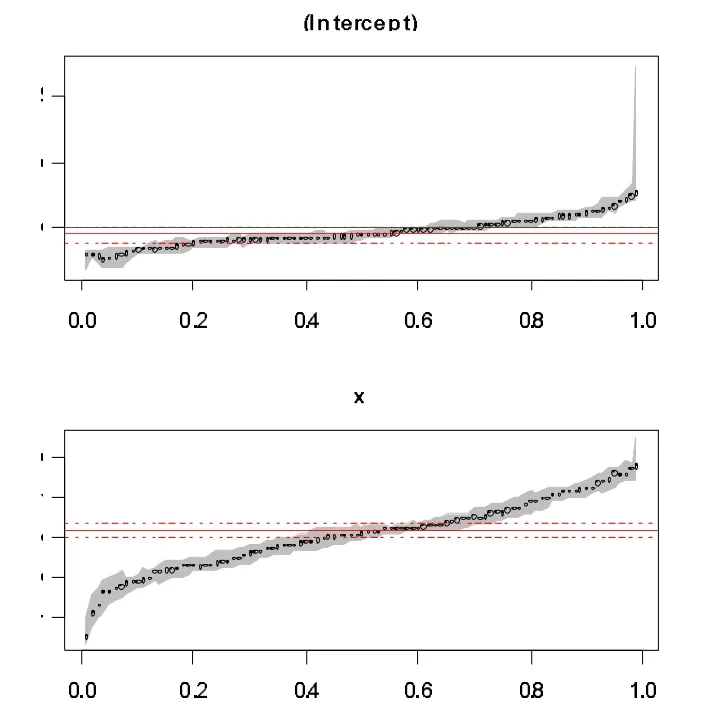
图4 异方差时在各分位点的变化

3.2 实例研究：社会支持对于心理健康的回归分析

关于社会支持对于心理健康的影响，许多心理学研究者如梁铁成（2007），钱胜等（2008）在不同地区、不同职业群体中都对该问题进行了研究，大多数研究表明社会支持可以促进心理健康。其中社会支持变量以社会支持评定量表（SSAS）的总分为指标，SSAS分数越高则被试受到的社会支持越多；心理健康变量以症状自评量表（SCL90）总分为指标，SCL90分数越高则其心理健康水平越低。

首先，对模型进行异方差的检验，检验方法除了观察散点图外，还可以使用一些统计量，如Park检验和Glejser检验。如果模型存在异方差，则异方差可能与一个或多个自变量系统相关。要确认这一点，可以做（或|ui|）对自变量X（或自变量的线性组合的回归。由于随机误差项ui难以观察，在实践中可以用ei代替ui。

如：

其中（3）式为Park检验，（14）～（16）式为Glejser检验。在本例中以上各式的参数估计结果如表2。

所有模型中α2系数都是统计显著的（P＜0.05），因此，存在异方差的情况，本例有使用QR模型分析之必要。分别使用传统的最小二乘回归分析和分位数回归方法分别对这批数据进行建模分析。在QR模型中，选取0.25、0.50和0.75三个分位点，代表因变量（SCL90总分）由低到高的3个水平。计算结果如图5所示。

表2 案例的异方差检验结果

图5 SCL90对SSAS的回归图

图5中的黑色实线是OLSR模型计算出来的回归线，回归线向下倾斜，说明自变量X（SSAS总分）的边际效果是负向的。SSAS总分越高，SCL90分数越低。社会支持对心理健康有正向的预测作用，与之前的研究结论一致。最小二乘回归方程为：

图5中的3条虚线由下到上依次对应着0.25、0.50和0.75共三个分位点上的QR回归线，它们对应的回归方程分别是：

表3 各百分位点上回归方程的参数估计结果

与OLSR的结果一致的是：3个QR模型的回归系数估计值都是负的，即证实了社会支持确实对心理健康具有正向的预测作用。而与OLSR不同的是，QR模型揭示了因变量不同水平上，回归系数的大小并不恒定，而是变化的。见表3。

随着分位点τ逐渐增大，自变量的回归系数越来越小（绝对值越来越大）。25%的回归线可用来代表SCL90总分处于较低水平的一类被试群体（心理健康状况较好的被试），则在这一层的被试群体中，社会支持每增加1个单位，SCL90总分将恰好减少1个单位。即社会支持能促进心理健康，边际效果为1.00。

相对应的，75%的回归线则可以代表SCL90总分处于较高水平的一类被试群体（心理健康水平较差、可能存在心理问题或心理障碍的被试），在这一层的被试群体中，社会支持每增加1个单位，SCL90总分将减少3.41个单位。即社会支持能更好的促进心理健康，边际效果为3.41。同理可知，SCL90总分处于中等水平的被试群体，社会支持对心理健康的边际效果为1.89。

综上所述，社会支持确实会促进心理健康，但是社会支持的影响力是受被试当前的心理健康状态影响的。对于心理健康水平较差的人，社会支持的效果更明显；对于心理健康水平较好的被试，或许由于自身已具有较强的自我调节能力，外界的社会支持因素所起的作用相对较小。

4 结论

以条件均值为目标函数的最小二乘回归模型具有意义直观、计算简明等优点，且根据Gauss-Markov定理证明，其参数估计值为最优线性无偏估计值。但是最小二乘回归模型需要满足严格的假设要求，其中包括同方差假设。

当同方差假设无法满足时，尤其是当误差方差呈现有规律的递增或递减时，最小二乘回归参数估计的有效性将无法保证，进而可能导致误差方差的有偏估计和F检验、T检验的失效。此时分位数回归具有明显的优势。

在异方差条件下，回归系数的估计值会随着分位点的不同而发生变化，而分位数回归可以将这些层次间的差异分离出来，在不同的因变量水平上分析自变量对因变量的影响，从而全面、动态地刻画出变量间局部 “特殊”的回归关系。而最小二乘估计则将这些差异相互抵消了，以一条“平均的”回归线概括了总体信息，同时也掩盖了各个局部的信息。

分位数回归和最小二乘回归实际上是一种互为补充的关系。分位数回归既不是要替代传统的最小二乘回归，也并未与其存在矛盾。若观测数据满足同方差假设时，最小二乘回归可提供最优无偏估计值；若观测数据出现异方差情况，则恰好可以发挥分位数回归的强大分析能力，挖掘出不同分位点上，尤其是因变量的高低水平上不同的回归关系。两个回归模型并无优劣之分，只有结合研究背景和数据分布情况，合理选择方法，才能最大限度地发挥统计方法的优越性，提高研究的效率和精度。

[1]Koenker R，Bassett G.Regression Quantilez[J].Econometrica，1978，(46).

[2]Koenker R，Bassett G.Robust Tests for Heteroscedasticity Based on Regression Quantiles[J].Econometrica，1982，(50).

[3]Gujarati D.N，张涛.计量经济学精要[M].北京：机械工业出版社，2000.

[4]焦璨，王宣承，张敏强等.分位数回归：心理统计方法的重要补充[J].中国考试，2009，(1).

[5]梁铁成.警察心理健康状况之调查[J].中国健康心理学杂志，2007,15 (11).

[6]钱胜,王文霞,王瑶.232名河南省农民工心理健康状况及影响因素[J].中国健康心理学杂志,2008,(04).

[7]张敏强.教育与心理统计学[M].北京:人民教育出版社，2002.