不重复抽样下总体比例的估计
2011-03-09管宇
管宇
(浙江农林大学 统计系,浙江 临安 311300)
0 引言


其中,z为标准正态分布的分位点Φ(z)=1-α/2,1-α是置信概率或称置信水平。由于超几何分布是离散分布,而正态分布是连续分布,因此考虑对其进行连续性修正[1,2]:

正态近似产生的误差主要与P和n相关,P接近于0和1时误差相当大,文献[1]列出了正态近似的最小np值与n值。
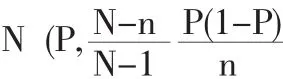

除正态近似外,Burstein[4]提出由二项分布近似超几何分布而借用二项参数的置信区间略作修正近似成为p的置信区间,当然此时二项参数的置信区间要尽可能准确。本文研究比较区间CI1、CI2、CI3的统计性质,以决定它们的取舍。
1 范围概率
设总体比例P未知,经不重复抽样得样本比例p,约定置信水平1-α。设[L(p),U(p)]为P的一置信区间,在常规意义下区间估计应该满足

但是,超几何分布是有限离散随机变量,除极个别点P值外,对于(0,1)区间中的几乎所有P值来说,等式(4)精确成立是不可能的。为此,我们称P{L(p)≤P≤U(p)}为置信区间[L(p),U(p)]的范围概率,简记CP{L(p),U(p)}或CP。如果要求对所有P∈(0,1),都有CP≥1-α,这样的区间称为精确置信区间(Exact confidence level);特别地,人们希望这些区间的长度都是最短的,此时称为短的精确置信区间[5]。不难想象精确置信区间是没有简单的显式表达形式的,必须借助计算机进行编程运算才能获得。因此,统计家们作出了各种短的精确置信限表以方便人们需要时查阅。我国国家标准库“数据的统计处理和解释”中就有一些置信限表,如GB/T 10094-2009正态分布分位数与变异系数的置信限、GB/T4087-2009二项分布可靠度单侧置信下限等。
另外,精确置信区间要求范围概率不得低于置信水平,必然造成在某些时候估计过于保守。假若对于某P值,有两个置信区间I1和I2(表达式复杂程度一样),它们的范围概率分别等于0.956和0.948,那么恐怕大多数人会选择I2而不要I1,虽然前者的范围概率低于要示的置信水平0.95,但其与0.95的绝对误差明显小于后者。因此,寻找与置信水平误差较小而表达式简单的近似置信区间具有非常现实的实用价值。
定理1置信区间CI1、CI2、CI3对应的范围概率分别为
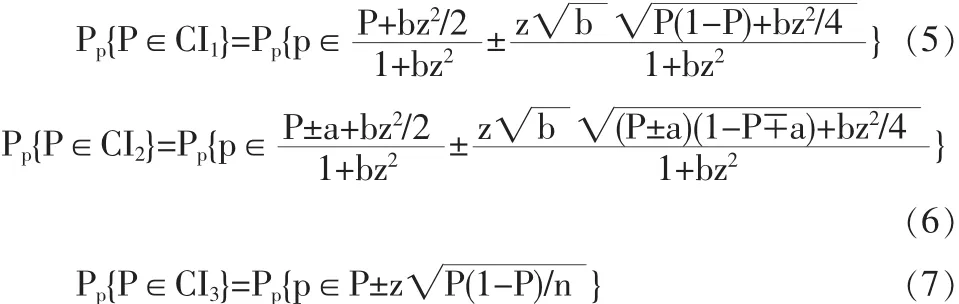
吴喜之[6]指出置信区间CI1的下限可能会出现负值,其实我们只需要将负值下限修改为0,同样地凡遇到大于1的上限修改为1。由于这不是问题的关键,通常文献中(如[5])都不特别强调,只要在使用(本文区间CI1、CI2、CI3和它们的范围概率)时略加注意就行。
置信区间CI1和CI2因为表达式简单而广泛地出现在统计手册[7]和“抽样技术”教材[1,2],CI3则表达形式略显复杂。表1和图1列出了这三个区间的范围概率的一些数据,其中表1中N=10000、M分别取遍1至9999所有整数,minCP表示P= M/N中范围概率的最小值即最坏的范围概率,n2-、n1-、n1+、n2+分别为范围概率与置信水平的差落入区间 [kα/5,(k+1)α/5)(k =-2,-1,0,1)的比例。显然n1+越大越好,其次是n1-+n1+越大越好。如水平1-α=0.90、0.95、0.99时,n1-和n1+分别代表落入区间[0.88,0.90)和[0.90,0.92)、[0.94,0.95)和[0.95,0.96)、[0.988,0.99)和[0.99,0.992)。
图1显示了H(10000,M,100)对应的区间CI1、CI2、CI3的范围概率曲线,M取遍1至5000的所有整数,P=M/N。因超几何分布关于M对称的,故只需显示一半即可。CI1的范围概率明显偏小,特别是水平0.99时只有2%多点达到0.99。CI2在水平0.90和0.95时偏保守,但在水平0.99时则只有约1/ 3达到目的0.99,不同水平下范围概率分布不平衡。而且CI1和CI2的最坏情形时范围概率都只有0.1,当M/N<0.05时它们的范围概率都明显小于置信水平。区间CI3的范围概率绝大部分都在置信水平附近,对于水平0.90、0.95、0.99相应的n1-+n1+分别是达到88%、85%、73%;只有M/N<0.02时范围概率才有些大的波动,但最坏时与置信水平差距最多约0.1。表1中的后六行列出H(10000,M,20)和H(10000,M,2000)相应区间CI3范围概率数据,显然抽样样本容量n越大,范围概率分布越集中于置信水平附近,区间CI3估计效果越好;样本容量n越小,范围概率分布越分散,估计效果略差些。但是,即使样本容量n只有20(抽样比f=0.002),最坏情形与置信水平相差至多约0.11。

图1 H(10000,M,100)的置信区间CI1、CI2、CI3(行:自下往上)对应于置信水平0.90、0.95、0.99(列:从左往右)的范围概率曲线

表1 区间CI1、CI2、CI3的最小范围概率和落入置信水平附近区域的比率
2 结论

[1]Cochran W G.抽样技术[M].张尧庭,吴辉译.北京:中国统计出版社,1984.
[2]李金昌主编.应用抽样技术[M].北京:科学出版社,2007.
[3]雷钦礼.总体比例置信区间的确定[J].山西财经学院学报,1996,(2).
[4]Burstein H.Finite Population Correction for Binomial Confidence Limits[J].Journal of the American Statistical Association,1975,70 (349).
[5]Kabaila P,Byrne J.Comparion of Poisson Confidence Intervals [J].Communications in Statistics-Theory and Methods,2005,34.
[6]吴喜之.不同总体量和样本量时如何计算比例的置信区间[J].统计与信息论坛,2005,20(3).
[7]茆诗松主编.统计手册[M].北京:科学出版社,2003.
