圆形隧道围岩与衬砌渗透力解析解*
2011-02-27王建宇
郑 波 王建宇
(中国铁道科学研究院1) 北京 10081)(中铁西南科学研究院有限公司2) 成都 610031)
根据地下水处治方法的不同,修建于地下水位线以下的隧道通常可以分为“全堵型”、“排水型”2种.在“全堵型”隧道中,衬砌不透水,作用在衬砌上的水压力为静水压力,是一种表面力;而对于“排水型”隧道,围岩和衬砌都是透水的,由于地下水的流动,作用在衬砌与围岩上的水压力为渗透力,是一种体积力[1-2].
不排水的“全堵型”隧道衬砌类型在地下水头不超过30 m的地方广泛应用,大量工程实践表明,40~60m水头是“全堵型”结构的临界水头[3-4].当地下水位超过衬砌结构所能承受的临界水头时,“全堵型”衬砌类型不适用,同时,由于“以排为主”的设计原则已经不能适应当前水环境的保护[5],所以“以堵为主,限量排放”的地下水处治方法在隧道建设中得到了极大发展,大部分隧道衬砌被设计成透水的.本文回顾了国内外有关隧道围岩渗透力的研究,然后推导了轴对称模型中围岩与衬砌及注浆圈范围内渗透力解析公式.
1 隧道围岩渗透力研究现状
Bouvard等[6]于1969年提出围岩渗透力可以表示为

式中:γw为水的重度;h为地下水位线至隧道中心距离;r为隧道半径;R是指由渗透力引起的围岩孔隙水压力变化为零时隧道圆心到该处的距离.
Schleiss[7]于1986年建议用地下水位线与隧道中心的垂直距离h代替Bouvard公式中的R,例如,当h=R时

Fernandez等[8]于1994年使用镜像法提出

式中:θ为以隧道中心为原点,以拱顶为起点顺时针方向旋转的角度,其他符号标记与式(1)相同.
从式(2)、式(3)可以看出,当h/f→1时,即ln(h/r)→0,有 fS→∞、fF→∞(θ=0°),这与实际情况不符合.
Kyung-Ho Park等[9]于2008年采用保角变换推导了2种不同边界条件下的围岩渗透力.
1)当考虑衬砌背后孔隙水压力为零时,围岩渗透力有

2)当考虑作用在衬砌上水头为hr时,围岩渗透力有

式中:θ′为以隧道中心为原点,以边墙点为起点逆时针旋转的角度;A=h(1-α2)/(1+α2);α=(h-为地表面到其上水位线距离,见图1.若地下水位线低于地表时,式(4)、(5)中H =0;h为地下水位线至隧道中心的垂直距离.

图1 水下隧道计算示意图
2 隧道围岩与衬砌渗透力计算理论
假设岩体在水力学特性上为连续介质,地下水对围岩和衬砌结构上的作用力可用分布在围岩和衬砌上的场力表示,即渗透力.同时假设水体不可压缩,在岩体与衬砌中的渗流符合Darcy定律.
根据Darcy定律,在岩体中水流流速可以表示为
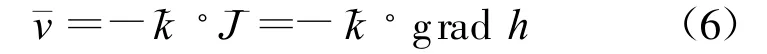
稳定地下水流在围岩与衬砌中的水力势场满足Laplace方程

对于轴对称问题,连续性方程可以表示为:Q =const(r),即通过每个环形隧道断面的渗流量是相等的,与半径无关.
在给定Z轴向上为正的坐标系中,水力势可以表示为

式中:γw为水的重度;u为渗透水流流速;g为重力加速度.
由于流体在孔隙介质中的流速通常较小,水力势可以简化为

在地下水引起的渗流场中,孔隙水压力p的梯度即为渗流荷载,结合式(9)可得
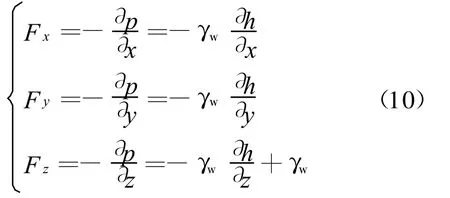
渗流荷载是体积力,它可以分解为渗透力 fs与浮力 fb,分别表示如下
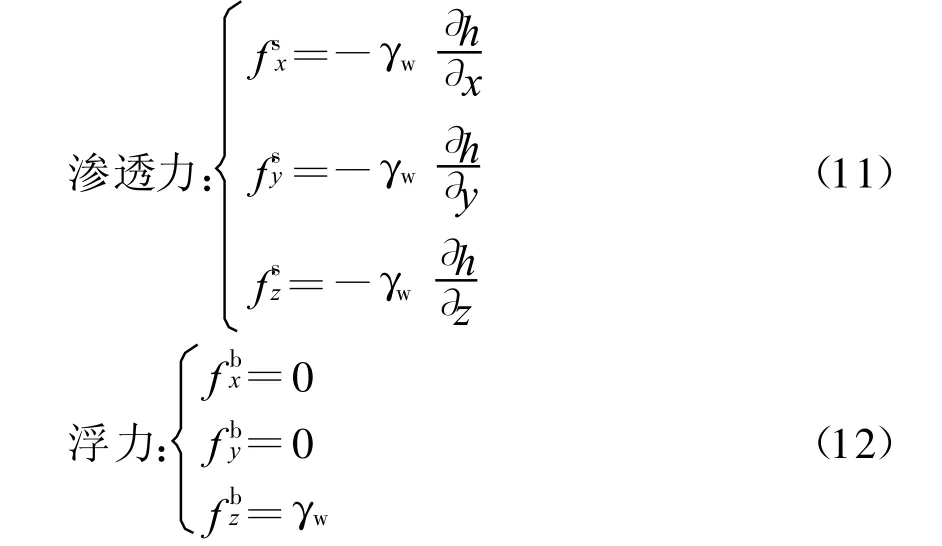
对于轴对称问题,渗透力可以表示为

3 退化圆形隧道围岩与衬砌渗透力
本文对于退化轴对称问题主要考虑隧道位置处水头小于隧道埋深(如深埋山岭隧道)情况,不考虑隧道位置处水头大于隧道埋深的情况.
依据无限含水层中井理论,把深埋隧道中隧道围岩、衬砌渗流概括为承压水向垂直井的运动.并假定隧道断面为圆形,围岩为各向同性均匀连续介质,地下水渗流满足渗流连续性方程和Darcy定律,远水势恒定为 H,不计初始渗流场及相应的渗透力,见图2.且令:ks为衬砌渗透系数;km为围岩渗透系数;kg为注浆圈渗透系数;r为研究点的极距;r0为衬砌内径;r1为衬砌外径;rg为注浆圈外径;h1毛洞状态下水力势;h2带注浆圈的衬砌后水力势;H为远场水力势.

图2 轴对称圆形隧道计算示意图
3.1 开挖后,衬砌前
将指向隧道内的流量Q规定为正值,根据Darcy定律有Q/2πr=kmdh1/dr,考虑边界条件r =r1,h1=0,r=H,h1=H,对上式分离变量,然后积分可得衬砌前流量

将式(14)代入Darcy定律,可得毛洞状态下围岩水力势

结合式(13)、(15)可得毛洞围岩渗透力

3.2 衬砌后
衬砌后,隧道围岩中水力势场由毛洞状态下的h1变为h2,在衬砌范围(r=r0~r1)内,有Q/2πr=ksdh2g/dr,考虑边界条件r=r0,h2s=0,可得

在注浆范围(r=r1~rg)内,有Q=/2πr= kgdh2g/dr,考虑边界条件r=rg,h2g=h′2g,可得
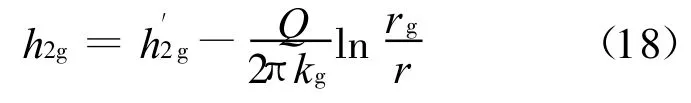

在r=rg边界上,即注浆圈与围岩交界处,根据水力势的连续性有h2g=h2m,把式(19)代入式(18)可得注浆圈范围内水力势为
在围岩范围(r=rg~H)内,有Q/2πr= kmdh2m/dr,考虑边界条件r=H,h2m=H,可得

根据连续性方程,当r=r1,由式(17)、(20)计算的结果也应该相等.故可以得出衬砌后流量为

联合式(17)与(21)可得衬砌范围内水力势

当r=r1,并考虑 H≫r1时,衬砌背后的孔隙水压力

对式(22)取r导数,求出dh2s/dr代入式(13),得衬砌范围(r=r0~r1)内的渗透力
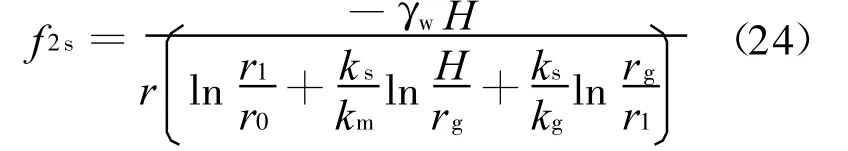
渗透力是一个体积力,通过对式(24)积分,可以求出衬砌范围(r=r0~r1)内渗透力的合力
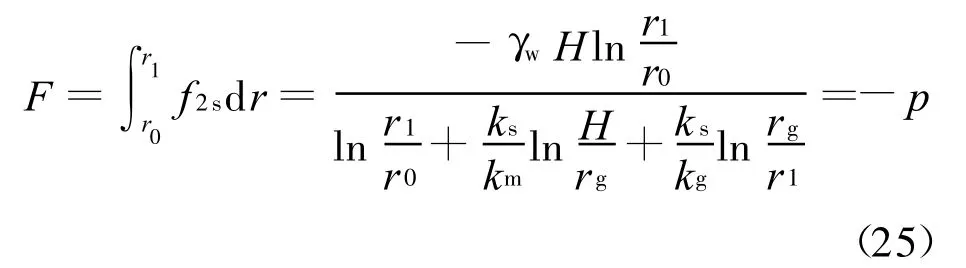
联合式(20)与(21)可得注浆圈范围内水力势

同理,对式(26)取r的导数,求出dh2g/dr代入式(13),可得注浆圈围岩范围(r=r1~rg)内的渗透力
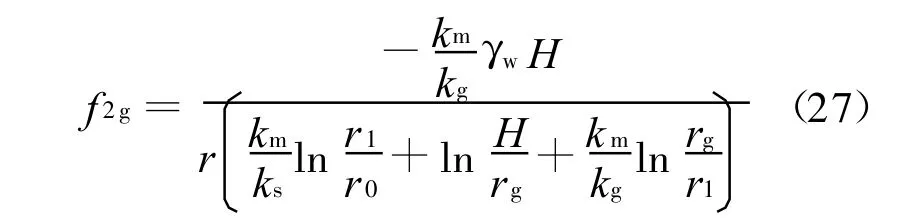
联合式(19)、(21),可得围岩范围内水力势

对式(28)取r的导数,求出dh2m/dr代入式(13),可得围岩范围(r=rg~H)内的渗透力

从式(23)可知,当衬砌不透水(ks=0)时,作用在衬砌上的水压力量值为p=γwH,即该点的静水压力.若堵水注浆圈能够完全堵住外水渗入时,即kg=0时,那么作用在注浆圈壁上的水压力量值为p=γwH,亦为该点处的静水压力.总之,当计算边界或内部有不透水面时,则在不透水面法向作用有量值为孔隙水压力p面荷载.所以,作用在全封堵型衬砌上的水压力值就是相应点的静水压力.
结合式(16)与(29),可知隧道衬砌前后围岩中渗透力的增量

这表明,由于围岩受到“衬砌效应”作用,围岩中渗透力增量系背向隧道中心的;而由式(24)可知,作用在衬砌上的渗透力是指向隧道中心的.
4 渗透力公式比较分析
目前文献中所能查阅到的渗透力公式,只考虑作用在衬砌上的水头及隧道半径对渗透力的影响,没有考虑围岩与衬砌的渗透系数对渗透力的影响.显然,围岩与衬砌的渗透系数对渗透力的影响是不可忽略的,例如,当隧道处水类型为“全堵型”时,作用在衬砌上的水压力为该处的静水压力,而围岩中的水没有流动,可以认为渗透力等于0.即使是“排水型”隧道,也与排水强度有关,即与衬砌渗透性有关.
在渗透力比较分析中,对式(4),考虑H=0;对式(5),取H=0,hr=-h;而对本文推导的公式,以某海底隧道的服务隧道为计算模型,该隧道为锚喷支护结构,取隧道围岩渗透系数km为3.7 ×10-5cm/s,考虑衬砌混凝土的裂缝情况取其渗透系数ks为1×10-6cm/s,衬砌内径r0=3.0 m,衬砌外径r1=3.2 m.
图3为隧道渗透力与r/h关系曲线.f(S), f(1m)公式假设计算模型为轴对称问题,故在隧道拱顶、拱腰、仰拱处,2式给出的渗透力结果基本相同,且当r/h=0.3时,渗透力最小,但相对其他渗透力公式来说其结果偏大;f(2m)公式是所有渗透力公式中计算值最小的,主要原因是该公式考虑了衬砌对渗透力的影响,但由于计算中取km/ks=37,在拱顶、仰拱处,衬砌渗透性对渗透力的影响相对f(1K)公式来说并不明显.从理论上讲,当r/h→1时,围岩渗透力会不断减小,所以除了f(1K),f(2m)外,其他渗透力公式计算值与工程实际不符,故最适合描述围岩渗透力的是本文所提出的考虑衬砌渗透性的公式f(2m),且公式f(1m)为隧道不衬砌时公式f(2m)的特例.
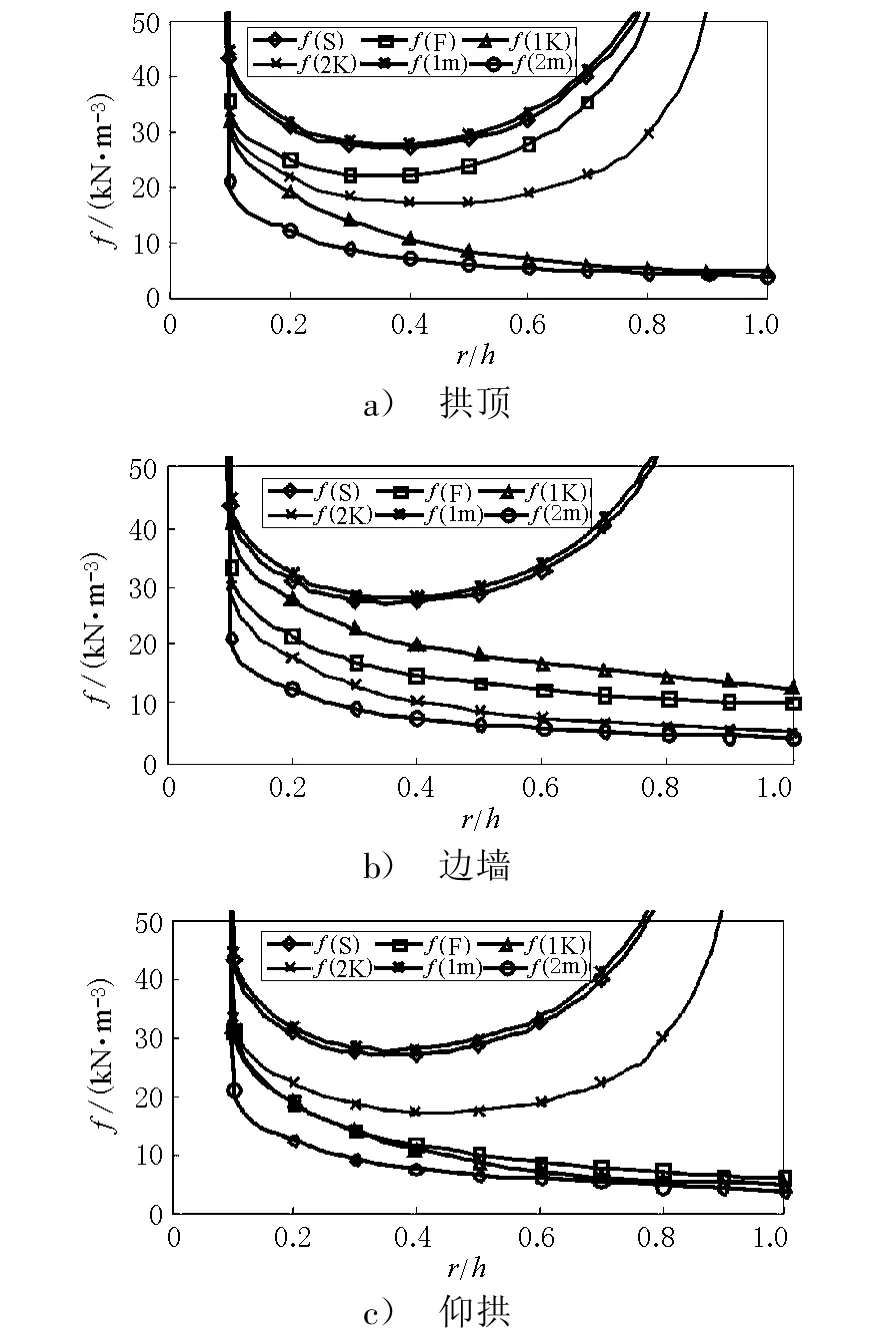
图3 围岩渗透力与r/h关系曲线
为了进一步研究衬砌渗透性对围岩渗透力的影响,图4给出了不同km/ks条件下f(2m)公式计算的围岩渗透力,图中n为km/ks比值,由图可以看出,当n=1时,即当于隧道开挖后不衬砌时,有 f2m=f1m,围岩最小渗透力为29.87 kN/m3.当n>1时,围岩渗透力随着 n值增大而不断减小,当n>50时,km/ks比值对围岩渗透力影响不大.

图4 f(2m)公式计算的围岩渗透力
5 结论与存在问题
1)国内外现有的围岩渗透力公式未考虑衬砌渗透性对围岩渗透力的影响,与实际工程不符.
2)依据无限含水层中井理论推导了轴对称条件下围岩、衬砌渗透力公式,并考虑了注浆圈对围岩、衬砌渗透力的影响.
3)通过不同渗透力公式计算结果的对比分析可知,衬砌渗透性对围岩渗透力的影响很大,不能被忽略.当围岩渗透系数与衬砌渗透系数比值n值增大时,围岩渗透力会不断降低,但当n>50时,km/ks比值对围岩渗透力影响不大.
4)本文推导的渗透力公式是在轴对称条件下得出的,与实际工程问题相比可能仍存在一定差距,有待于在以后的工作中进一步改正和完善.
[1]Kolymbas D,Wagner P.Groundwater ingress to tunnels-the exact analytical solution[J].Tunnelling and Underground Space Technology Incorporating Trenchless Technology Research,2007,22(1):23-27.
[2]Nam S W,Bobet A.Liner stresses in deep tunnels below the water table[J].Tunnelling and Underground Space Technology Incorporating Trenchless Technology Research,2006.21(6):626-635.
[3]南泽寿,朱银贞,崔圭哲.海底隧道衬砌-地基的水力相互作用[J].岩石力学与工程学报,2007,26(增2): 3 674-3 681.
[4]王建宇.隧道围岩渗流和衬砌水压力荷载[J].铁道建筑技术,2008(2):1-6.
[5]蒋忠信.隧道工程与水环境的相互作用[J].岩石力学与工程学报,2005.24(1):121-127.
[6]Bouvard M,Pinto N.Amenagement capivari-cachoeira.etude du puits en charge[J].Houille Blanche, 1969,7:747-760.
[7]Schleiss A.Design of previous pressure tunnels[J]. International Water Power and Dam Construction, 1986,38:21-26.
[8]Fernaondez G,Alvarez T A L.Seepage-induced effective stresses and water pressures around pressure tunnels[J].Journal of Geotechnical Engineering, 1994,120(1):108-128.
[9]Park K H,Lee J G,Owatsiriwong A.Seepage force in a drained circular tunnel:an analytical approach [J].Canadian Geotechnical Journal,2008,45(3):432-436.
