一类Riccati型方程的可积条件及通积分
2011-02-20王玉萍
王玉萍
(陕西科技大学理学院, 陕西 西安 710021)
0 引 言
法国数学家刘维尔(Liouville)在1841年证明了著名的黎卡提(Riccati)方程
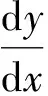
(1)
一般是不可积的,即不能用初等积分法求解.由于它在流体力学和弹性振动理论等领域有广泛的应用,因此,对Riccati方程的求解仍不失时代意义.许多学者对Riccati方程的可积性做过大量研究[1-8].本文将Riccati方程(1)推广成Riccati型方程:
(2)
利用变量代换的方法,给出其可积性的几个充分条件及其对应的通积分.值得一提的是,所得一些结果既包含了已有文献中的一些结论,同时也丰富了Riccati方程的可积性理论.

1 主要结论
定理1 若存在可微函数φ=φ(x)满足:
(3)
则方程(2)可积且对应的通积分为
(4)
证明 作变换
(5)

把y,y′代入方程(2)得
整理得
由条件(3)得,u′=Pu2+(Q-2φ)u,这是伯努利方程,其通解为
故方程(2)可积,由式(5)得式(2)的通积分为式(4).
证明 在定理1中令φ=Q即得.
注 在推论中取f(y)=y,可得方程(1)可积的条件及通积分.
推论1.2 若R=Q-P,则方程(2)可积且通积分为
证明 在定理1中令φ=P即得.
证明 在定理1中令φ=R即得.
推论1.4 若R=Q2(1-P)-Q′,则方程(2)可积且通积分为
证明 在定理1中令φ=PQ即得.
证明 在定理1中令φ=Q/2即得.
注:在推论1.5中令f(y)=y,则结论为文献[7]的定理4.

定理2 若存在函数φ=φ(x)满足
(6)
则方程(2)可积且通积分为
(7)
(8)
将式(7)、(8)代入方程(2)得
所以
(9)
这是一个以u为未知元的Riccati方程,由条件(6)及引理知方程(9)可积且其通积分为

由式(7)得方程(2)的通积分为
证明 在定理2中令φ=0即得.
注:在定理2中令f(y)=y即得引理,显然引理是定理2的推广.
证明 在定理2中令φ=-Q即得.
推论2.3 若存在k≠0,使得P=kQ-k2R,则方程(2)可积.
证明 在定理2中令φ=Q-kR(k≠0常数)即得.
注:当取k=1,得R=Q-P时可积,这与推论1.2可积性结论一致. 当取k=1/K,则结论为文献[3]定理4.

整理得

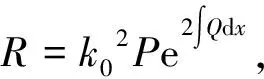
注:在定理及推论中取f(y)=y,可得方程(1)可积的一系列条件,从而扩大了Riccati方程可解的范围.
2 举例

解 该方程变形为
(10)
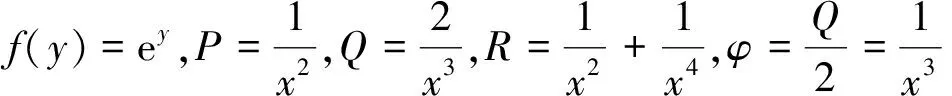

(11)
参考文献
[1] 冯录祥.关于一类Riccati方程可积性条件的注记[J].科学技术与工程,2010,10(18):4 469-4 471.
[2] ZHAO Lin-long. The intergrable condition of Riccati differential equation[J]. Chinese Quarterly Journal of Mathematics, 1999, 14(3):67-70.
[3] 冯录祥.一类Riccati方程的推广[J].数学的实践与认识,2000,30(2):235-239.
[4] 窦霁虹. Riccati方程的可积性条件[J].纯粹数学与应用数学,2006,22(1):19-24.
[5] 王玉萍. Riccati型微分方程可积性的充分条件[J].陕西科技大学学报,2006,(6):141-143.
[6] 冯录祥,魏列萍.Riccati方程可积的若干充分条件[J].咸阳师范学院学报,2000,(3):16-18.
[7] 赵有为.Riccati方程可积的一些可积形式[J].益阳师专学报,2000,17(5):6-8.
[8] Li Hongxiang.Elementary quadratures of ordinary differential equations[J].Amer.Math. Monthly,1982,89(3):198-208.
