多属性采购拍卖的竞争策略研究

陈德艳

(辽宁石油化工大学理学院， 辽宁 抚顺 113001)

0 前 言

采购拍卖作为逆向拍卖中的一种，由于能够有效地降低成本而被广泛应用于政府和企业的采购之中，特别是随着电子商务的迅速发展，其所具有的能够降低采购价格、节约管理费用与减少库存水平的优点使得网上采购拍卖成为企业采购的主要方式.而参加逆向拍卖的供应商也能够通过网上采购拍卖获得新的市场机会，提高市场占有率，缩短竞标与获得合同的时间，并提高生产计划和库存管理的水平[1，2].但是对大多数的逆向拍卖而言，还要考虑除了价格属性以外的其他属性的影响，即考虑双方在价格以外其他属性上进行多重谈判的多属性拍卖模式[3，4].Che最早对多属性拍卖进行了完整的分析，通过引入得分函数提出了一种涉及质量和价格二维属性的拍卖模型[5].Branco推广了Che的模型，提出了供应商成本相关情况下的多属性拍卖模型[6].Mishra等首次把多属性拍卖划分到采购经济的研究范畴之中，为供应商提供了投标策略模型，证明了拍卖竞争性均衡的可实现性[7].本文正是在Che模型的基础之上，提出了在拍卖人设置进入费用的情况下考虑两个质量属性和价格属性的三维拍卖模型，给出了供应商的最优投标策略，并设计了采购商的最优拍卖模型，给出了最优得分函数.

1 模型的假设

本文的模型当中要考虑到两个质量属性和价格属性的三维投标模型，其中的质量指标可以是采购商品的技术特征、交货日期、服务可靠性等等.模型当中有一个采购商，n个供应商，所有供应商全部参加拍卖投标，并交纳一定数量的入场费，采购商是拍卖规则的制定者.采购商采购单一物品，并且设计一个得分函数，供应商密封投标竞争，采购商通过得分函数对供应商的投标进行打分，得分最高的供应商中标.模型的基本假设如下：

假设1：供应商i(i=1,2,…，n)的进入费用为常数δ，该费用相对于采购物品的价值而言较小.

假设3：供应商的投标向量为(q1,q2,p)，这里q1为采购商品的第一个质量属性投标，q2为采购商品的第二个质量属性投标，p为采购商品的价格投标.

假设4：供应商的成本函数为c(q1,q2,θ)，成本为凸函数并且满足cq1>0，cq2>0，cθ>0，cq1q1≥0，cq2q2≥0，cq1θ>0，cq2θ>0，cq1q1θ≥0,cq2q2θ≥0,不同供应商成本的不同主要是由成本参数θ决定.

假设5：供应商风险中性，供应商i获胜时的收益函数为πi=p-c(q1,q2,θ)-δ.

假设6：采购商的效用函数为U(q1,q2,p)=V(q1,q2)-p+nδ，其中Vq1>0，Vq2>0，Vq1q1<0,Vq2q2<0.

2 供应商的投标策略

2.1 供应商的投标策略分析

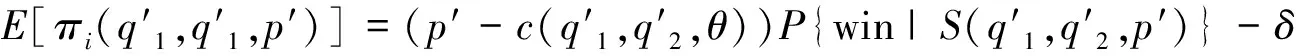
>(p-c(q1,q2,θ))×P{win|S(q1,q2,p)}-δ=E[πi(q1,q2,p)]

2.2 最优投标策略

定理1：在上述得分函数和基本假设下，供应商i的唯一对称均衡投标策略为：

证明：两个质量投标的结果在引理中可得，只证价格投标策略.

πi=(p-c(q1,q2,θ))×P{win|S(q1,q2,p)}-δ=(v-b)Hn-1(b-1(b))-δ

(1)

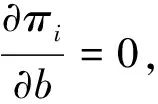
πi=(p-c(q1,q2,θ))Hn-1(v)-δ=(p-c(q1,q2,θ))(1-F(θ))n-1-δ

(2)

(1)、(2)两式联立可得价格投标为:

定理得证.

3 采购商的最优拍卖

根据显示原理，本文参考Laffont和Tirole Acfee[9]以及McMillan[10]的结果得出下面的引理.

引理2：最优的直接显示机制中，最低类型的供应商中标，其质量投标为：

证明：采购商的效用为U(q1,q2,p)=V(q1,q2)-p+nδ，根据引理2，最低类型的供应商中标，此时θ=θ1，可得采购商的期望效用为:

最大化采购商的期望效用，其投标质量的选择应满足一、二阶条件，即有

而在得分函数S(q1,q2,p)下供应商的质量投标分别为

4 算例分析

5 结束语

本文在Che模型基础之上，建立了两个质量投标，一个价格投标的最优多属性拍卖机制，在引入进入费用的基础上讨论了供应商的最优投标策略和采购商的最优得分函数的设置.本文与Che模型的不同之处在于引入了进入费用，增加了质量投标，同时要求采购商对市场的供应情况有一定的了解，大概知道供应商的最低成本类型；参与拍卖的供应商的个数不能太少.证明结果表明进入费用对供应商的最优价格投标有影响，会增加投标价格，但对质量投标没有影响，同时对采购商的效用没有影响；而得分函数的设置在保证一定数量的供应商的情况下也能够保证所用的拍卖机制为最优的直接拍卖机制;特别是本文给出了供应商类型服从均匀分布下的具体质量与价格投标的一个简单的计算公式，方便实用.文中算例中的效用函数[11]与成本函数的选择就是根据实际拍卖中的情况设置的，计算数值也验证了所证明的结果，所得结论可以为采购拍卖中双方的决策提供参考，从而提高采购拍卖的效率.

参考文献

[1] 田 剑，唐小我.在线逆向拍卖研究回顾与展望[J].电子商务与信息管理,2009,21(12)：57-62.

[2] 黄天柱.上市公司双重要约收购中的博弈分析[J].陕西科技大学学报，2008,(6)：172-174.

[3] 黄 河，陈 剑.采购组合拍卖投标均衡策略研究[J].系统工程理论与实践,2007,(10):93-97.

[4] Bichler M. An experimental analysis of multi-attribute auction[J].Decision Support Systems,2000,(29):249-268.

[5] Che Y K. Design competition through multidimensional auctions[J]. RAND Journal of Eonomics,1993,(24):668-680.

[6] Branco F. The design of multi-dimensional auctions[J]. RAND Journal of Eonomics,1997, 28(1):63-81.

[7] Mishra D. and Veeraman D. A multi-attribute reverse auction for outsourcing[C].Proceedings of the 13 th International Workshop on Database and Expert Systems Applications,2002:77-86.

[8] David E., Azoulay-Schwartz R., Krais S. Bidding in sealed-bid and English multi-attribute auctions[J]. Decision Support Systems, 2006, 42:527-556.

[9] Laffont J. and Tirole J. Auctioning incentive contracts[J]. Journal of Plitical Eonomy, 1987,95:921-937.

[10] Mcafee R.P. and Mcmillan J. Competition for agency contracts[J]. RAND Journal of Economics，1987,18:296-307.

[11] Bichler M. Kalagnanam J. An configurable offers and winner determination in multi-attribute auctions[J]. European Journal of Operational Research, 2005, 160(2):380-394.