高阶导数连续的凸轮从动件运动规律研究

王允地 ， 王稳地， 王良文， 张航伟

(1．陕西科技大学机电工程学院, 陕西 西安 710021； 2. 西南大学数学学院, 重庆 400715； 3. 郑州轻工业学院机电工程学院, 河南 郑州 450002)

0 引 言

在自动机械中，通常用凸轮机构实现从动件有停歇的往复运动.凸轮匀速转动一圈，从动件实现升程—远休止—回程—近休止4个过程.与从动件行程(升程或回程)对应的凸轮转角Ф称为行程角，做往复直线运动的从动件总位移h或做往复摆动的从动件总摆角Ψ称为从动件行程.以T表示凸轮转角φ与行程角Ф的比值，且称其为无因次时间，S表示从动件直线位移s与行程h的比值或从动件摆角ψ与行程Ψ的比值，且称其为无因次位移.在凸轮的轮廓给定后，S和T之间便有函数关系

S=S(T)

(1)

图1 无因次位移随无因次时间的变化曲线 图2 无因次位移、速度、加速度曲线

我们称这一函数关系为凸轮机构的无因次运动规律，以后简称位移规律.

显然，位移规律函数自变量和因变量的取值范围均为0到1，如图1所示.从理论上看，运动规律的形式有无穷多个，属于经典数学上的第三类无穷大.

另外，我们称S对T的一阶导数

V=dS/dT=V(T)

(2)

为机构的无因次速度规律，以后简称速度规律，而称S对T的二阶导数

A=dV/dT=A(T)

(3)

为机构的无因次加速度规律，以后简称加速度规律.

如图2所示，速度和加速度规律曲线自变量的取值范围仍为0到1，函数的最大和最小值则随运动规律的不同而取相应值.

经过思考及研究，我们设置一个样本函数g(T) ,让它与一个待定常数k的乘积对自变量T从0到1的积分为1，这样，该乘积对T从0到T的积分

(4)

便是一个运动规律函数.

为了实用及研究方便，我们设定样本函数g(T) 在起、终点数值为0，在区间内光滑连续，关于中心轴对称，且在中心轴两边单调变化.

凸轮机构在运动过程中，系统惯性力系是周期性变化的.根据数学及机械学的研究结果可知，运动规律函数S(T) 导数连续的次数越高，系统惯性力系富里哀展开式高阶分量趋近于0的速度越快，对于高速高精度分度凸轮机构、自动装配机床、印刷机等容易产生高阶谐振的系统的振动影响越小，且能有效的降低机器噪音.

以下在本文的正文中，我们先讨论符合设定要求的幂函数类运动规律，再讨论三角函数类运动规律，接着讨论指数函数类运动规律，最后对修正等速度类运动规律做补充讨论.

1 幂函数类运动规律

1.1 三次幂规律

首先，取样本函数g(T) 为g(T)=T(1-T)，运动规律函数则是

(5)

S(T)=3T2-2T3

(6)

V(T)=6T(1-T)

(7)

A(T)=6(1-2T)

(8)

从中看出，该规律的速度函数连续，加速度函数在起、终点有柔性冲击(加速度有突变).T等于1/2时，速度取最大值3/2；T等于0时，加速度取最大值6，T等于1时，加速度取最小值-6,但速度与加速度的乘积AV(与驱动力矩有关)在起、终点仍然为0.

1.2 五次幂规律

我们取样本函数g(T)为g(T)=T2(1-T)2,同样可以推得五次幂运动规律的表达式为

S(T)=10T3-15T4+6T5

(9)

V(T)= 30T2(1-T)2

(10)

A(T)=60T(1-T)(1-2T)

(11)

1.3 七次幂规律

取样本函数g(T)为g(T)=T3(1-T)3,推得七次幂运动规律的表达式为

S(T)=35T4-84T5+70T6-20T7

(12)

V(T)= 140T3(1-T)3

(13)

A(T)=420T2(1-T)2(1-2T)

(14)

1.4 九次以上的幂函数规律

取样本函数g(T)为g(T)=T4(1-T)4,推得九次幂运动规律的表达式为

S(T)=126T5-420T6+540T7-315T8+70T9

(15)

该规律的四阶导数函数也连续.

取样本函数g(T)为g(T)=T5(1-T)5,推得十一次幂运动规律的表达式为

S(T)=462T6-1 980T7+3 465T8-3 080T9+1 386T10-252T11

(16)

该规律的五阶导数函数也连续.

类似的不断取样本函数g(T)为g(T)=Tn(1-T)n,便可得到n阶导数函数也连续的更高阶幂函数规律.

2 三角函数类运动规律

2.1 简谐规律

我们取样本函数g(T)为g(T)=sin(πT),运动规律函数则是

(17)

由此得出简谐运动规律的表达式为

(18)

(19)

(20)

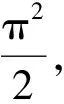
2.2 摆线规律

我们取样本函数g(T)为g(T)=sin2(πT),同样的可以推得摆线运动规律的表达式为

(21)

V(T)= 1- cos(2πT)

(22)

A(T)= 2πsin(2πT)

(23)

从中看出，该规律的加速度函数也连续.T等于1/2时，速度取最大值2；T等于1/4 时，加速度取最大值2π，T等于3/4 时，加速度取最小值-2π.

2.3 次摆线规律

我们取样本函数g(T)为g(T)=sin3(πT),同样的可以推得次摆线运动规律的表达式为

(24)

(25)

(26)

类似的不断取样本函数g(T)为g(T)=sinn(πT),便可得到n阶导数函数也连续的更高阶三角函数类运动规律.

3 指数函数类运动规律

3.1 初指数运动规律

我们取样本函数g(T)为g(T)=-eT-e1-T+e+1,同样可以推得初指数函数运动规律的表达式为

(27)

(28)

(29)

从中看出，该规律的速度函数连续，加速度函数有柔性冲击.T等于1/2时，速度取最大值1.493 8；T等于0时，加速度取最大值6.899 3，T等于1时，加速度取最小值-6.899 3,但速度与加速度的乘积AV在起、终点仍然为0.

另外，初指数规律速度V与加速度A乘积AV的最大值在上述诸规律中最低.

3.2 次指数运动规律

我们取样本函数g(T)为g(T)=(-eT-e1-T+e+1)2,同样的可以推得次指数运动规律，其加速度函数也连续.

图3 修正等速度运动规律

类似的不断取样本函数g(T)为g(T)=(-eT-e1-T+e+1)n,便可得到n阶导数函数也连续的更高阶指数函数规律.

4 修正等速度运动规律

在行程角Ф特别大的场合，可以优先考虑修正等速度规律，如图3所示.

4.1 四次幂修正等速度规律

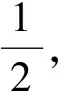
(30)

(31)

(32)

速度规律为

(33)

(34)

(35)

加速度规律为

(36)

A(T)=0T=δ～ 1-δ

(37)

(38)

4.2 简谐修正等速度规律

(39)

(40)

(41)

速度规律为

(42)

(43)

(44)

加速度规律为

(45)

A(T)=0T=δ～ 1-δ

(46)

(47)

5 结 论

(1) 通过设置不同的样本函数，可以得到各种各样的运动规律.

(2)按照这一思想，不仅得到了速度函数连续的三次幂规律、简谐规律及初指数运动规律，还得到了加速度函数连续的五次幂规律、摆线规律、四次幂修正等速度规律及简谐修正等速度规律，且得到了跃度函数连续的七次幂规律及次摆线规律，并给出了它们的特性值,导出了四阶导数连续的九次幂规律及五阶导数连续的十一次幂规律,指出了更高阶导数连续函数的获取途径.

(3)函数导数连续的次数增高，速度最大值及加速度最大值会有所增大,因此应根据具体情况适当选取.

(4)对于加工精度不高及要求驱动力矩较小的场合，可优先选用三次幂规律、简谐规律及初指数规律.对于加工精度较高且系统刚度较小的场合，则可选用五次幂规律、摆线规律、七次幂规律及次摆线规律.而对于运动过程较长的场所，则可优先考虑修正等速度规律.

参考文献

[1] 《数学手册》编写组.数学手册[M].北京：高等教育出版社，1998.

[2] 王允地,王稳地,王党会.机械系统的动力学稳定性研究[J].陕西科技大学学报，2005，23(1)：73-76.

[3] 杨 櫹.机床动力学[M].北京：机械工业出版社，1983.

[4] 杨义勇,金德闻.机械系统动力学[M].北京：清华大学出版社，2009.

[5] 张 策.机械动力学[M].北京：高等教育出版社，2008.

[6] 石端伟.机械动力学[M].北京：中国电力出版社，2007.

[7] 彭国勋,肖正杨.自动机械的凸轮机构设计[M].北京：机械工业出版社，1990.

[8] 尚久浩.自动机械设计[M].北京：中国轻工业出版社，2003.

[9] 刘昌祺,牧野洋,曹西京.凸轮机构设计[M].北京：机械工业出版社，2005.

[10] 孙 桓.机械原理[M].北京：高等教育出版社，2001.

[11] 华大年,唐之伟.机构分析与设计[M].北京：纺织工业出版社，1985.

[12] 楼鸿棣,邹慧君.高等机械原理[M].北京：高等教育出版社，1990.

[13] H.H.Mabie and F.W.Ocvirk. Mechanisms and Dynamics of Machinery[M].New York:John Wiley and Sons,1978.