阻尼减振材料滞弹性位移场模型参数寻优及其应用

曹友强，邓兆祥，2，王 攀，2，李 军

(1.重庆大学 机械传动国家重点实验室，重庆 400030;2.汽车噪声振动和安全技术国家重点实验室，重庆 400039)

在工程实践中，含阻尼材料的复合结构常被广泛用于抑制结构的振动和噪声［1］。粘弹性阻尼材料的本构模型决定了这类结构的动力学方程形式，由此可见阻尼材料本构模型的选用和计算尤为重要。由于粘弹性材料的本构关系随时间、频率和温度的变化而变化，使得粘弹性材料本构模型变得复杂多样，其参数优化计算也变得比较繁琐。目前大多数文献［2-5］都是直接采用经验参数代入本构模型进行计算，缺少对模型参数的优化选取。

由 Lesieutre［6，7］于 1995 年提出的滞弹性位移场(Anelastic Displacements Fields，ADF)模型从位移场的角度出发，将总的位移场分为弹性部分和滞弹性部分。ADF模型的辅助坐标在单元之间是连续的，体现了其位移场的特点，它能直接进行有限元解算，能很容易融入有限元动力学方程，因此受到众多学者的青睐［6-8］。但是，ADF模型各参数的确定是一个非线性、多变量、多目标规划，具有约束条件的优化问题，解决这一问题难度较大。针对此类问题的全局最优解没有任何数学条件可以表征，基于传统数学规划的优化方法因其优化结果易陷入局部极值而难以处理［9］，现代优化算法如遗传算法容易出现早熟状态，导致收敛时间长，优化失败［10］。

基于此，本文详细给出了基于粒子群算法(PSO)与序列二次规划法(SQP)相结合的求解方法。首先利用PSO算法的全局优化功能开展全局搜索，确定全局最优解的可行位置，再用SQP算法的局部精细搜索能力确定其局部最优解。文中建立ADF模型的优化模型，获取了ADF模型的各参数优化结果，并与标准流变模型、分数导数模型两种典型形式的松弛函数曲线进行拟合比较，由此验证了优化算法的可行性;通过对粘弹性集中参数系统及悬臂阻尼夹芯板结构的动力特性分析进一步验证了本文优化结果的准确性。这可为阻尼类材料本构模型的参数优化问题提供参考。

1 阻尼材料结构ADF数学模型

ADF材料模型［6-8］是基于热不可逆原理的连续场模型，用于描述粘弹性材料作一维剪切运动时的频率特性和温度特性。ADF模型将粘弹性材料在频域内的复模量模型表示为:

G*(ω)是粘弹性材料的复剪切模量，GA0对应于松弛弹性模量，Δi，Ωi，代表第i阶ADF模型的材料参数。n是非弹性位移场个数的总数目。如果有n阶摄动量，则需要确定2n+1个参数。

粘弹性材料ADF模型中弹性部分和滞弹性部分的关系可以通过引入一系列耗散辅助变量(i=1，…，n)表示:

式中，x是总的位移场，xe是弹性位移场是第i个滞弹性位移场。

考虑到粘弹性材料频变和温变特性，并假定粘弹性材料的泊松比为定值，则由虚功原理可获得含有粘弹性材料复合结构的动力学模型［8］为:

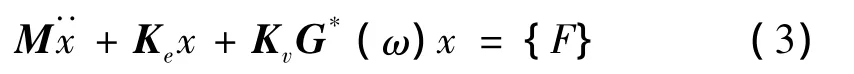
M是结构质量阵，Ke是结构弹性刚度矩阵，Kv是粘性材料刚度矩阵。

将xe替代(3)式中的粘弹性材料势能表达式中的x，再结合式(1)，则可得到ADF模型表征的粘弹性结构有限元方程:

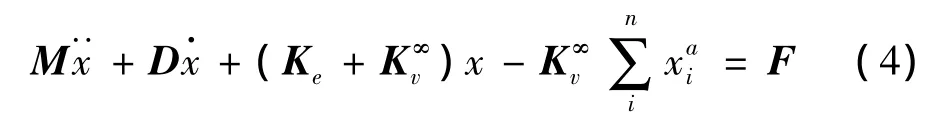
ADF模型中，描述粘弹性材料松弛行为的第i个滞弹性场松弛方程［7］:

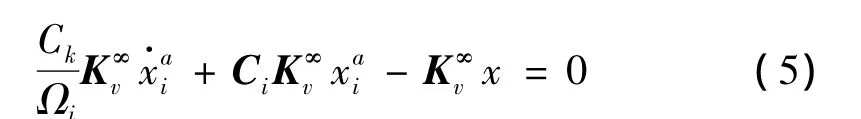
联合(4)、(5)，构成粘弹性阻尼结构动力学方程:

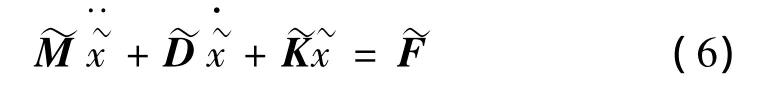
其中，

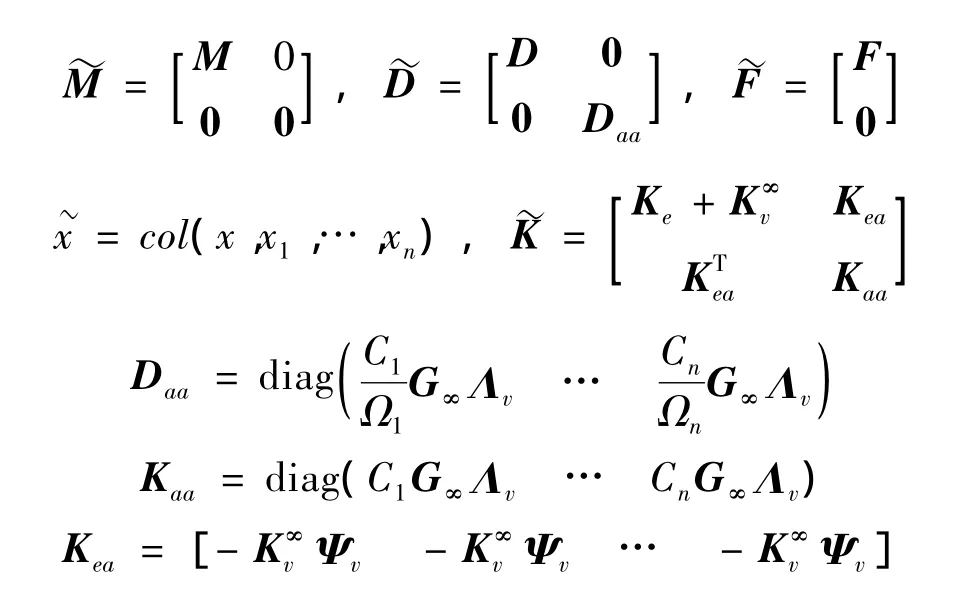
其中ΛV是由粘性材料刚度矩阵Kv的正特征值组成的对角阵，ΨV是以相应的正交特征向量作为列的矩阵。引入辅助变量后，ADF模型将复合结构用二阶线性模型加以描述，从而可以利用有限元理论开展分析。

2 混合PSO-SQP算法ADF模型多参数优化

阻尼材料ADF模型参数的确定本身具有非线性，包括2n+1个参数变量，又同时需要对模型的实部和虚部两个目标函数进行优化拟合，是一种典型的多参数多目标非线性优化问题。

考虑成非线性有约束全局多目标优化问题:

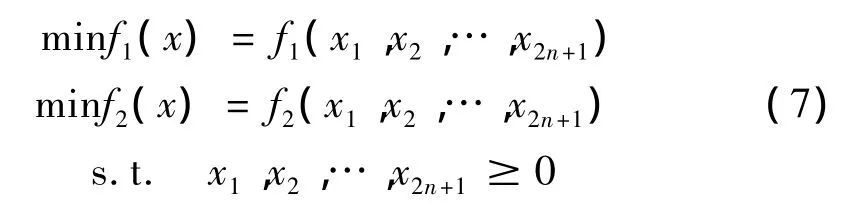
其中，f1(x)、f2(x)为实部和虚部两个目标函数，x为参数变量，n为ADF模型设定阶数。

2.1 混合优化算法原理

粒子群优化算法［11，12］是一种基于群智能的全局优化计算方法，具有收敛速度快、设置参数少、程序简洁等特点，但在优化后期 PSO算法的收敛速度明显变慢，甚至处于停滞状态，局部精细搜索能力有限。SQP算法［13］在具有整体收敛性的同时保持局部超一次收敛性，是求解非线性规划问题最优秀的算法之一，但对初值的选取有较强的依赖性。为了克服两种算法缺点 ，在PSO算法的后期引入SQP方法 ，利用 SQP方法整体收敛性和局部超一次收敛性来以获得很好的全局最优解。首先利用PSO算法的全局搜索能力确定出接近最优的可行解x0，再将x0作为SQP算法的初始点，进行局部精细寻优。在SQP算法搜索过程中，设定最大搜索迭代次数K，若超过最大搜索次数，则表明SQP算法陷入局部最优，同时说明上次PSO算法提供给SQP算法的结果不是一个良好的初值。此时结束SQP算法，同时在SQP算法所得的最后一次解x的较大范围内生成新的PSO算法种群空间。由此循环计算，直到SQP算法满足正常收敛。整个PSO-SQP混合算法操作在Matlab环境中编程实现。

2.2 优化目标模型

阻尼材料的力学性能一般在频域测定，所以ADF模型参数的确定也是在频域中通过曲线拟合获得。根据表达式(1)，令:

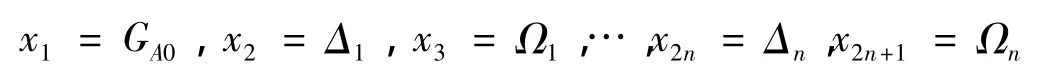
设定ADF模型在频域中的优化目标函数表达式:

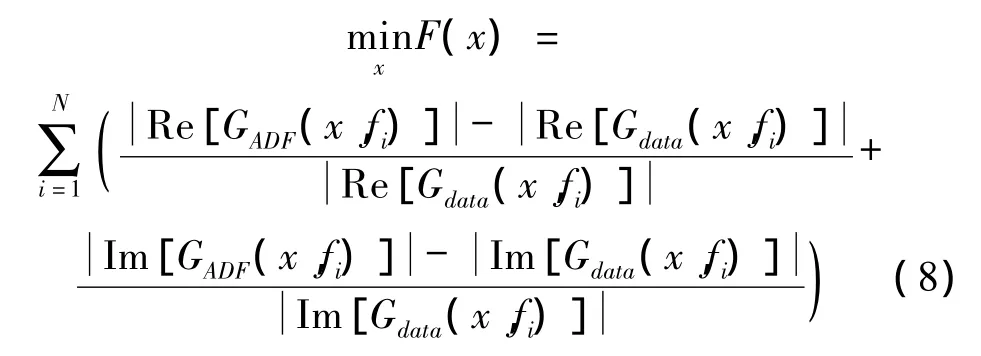
式中x=(x1，x2，…，x2n+1)为未知参数向量，N表示拟合的频率截点，GADF(x，fi)为ADF模型的复模量值，Gdata(x，fi)为阻尼材料通过试验或者相关材料阻尼模型得到的复模量随频率变化曲线值。

显然，对于阻尼材料ADF模型而言，上述目标函数为在xi＞0(i=1，2，…，2n+1)约束条件下的多变量优化问题，并且目标函数代入模型后表现出高度非线性、多极值的特点。

3 算例分析

3.1 ADF模型参数寻优

为比较本文寻优方法在优化选取多参数问题的可行性，将ADF模型摄动项n分别取2和4。将本文优化得到的ADF模型与分数导数模型、标准流变模型进行曲线拟合比较，见图1～图2。

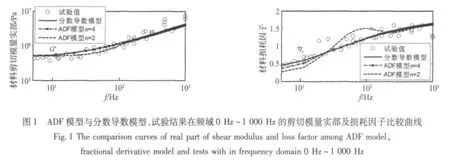
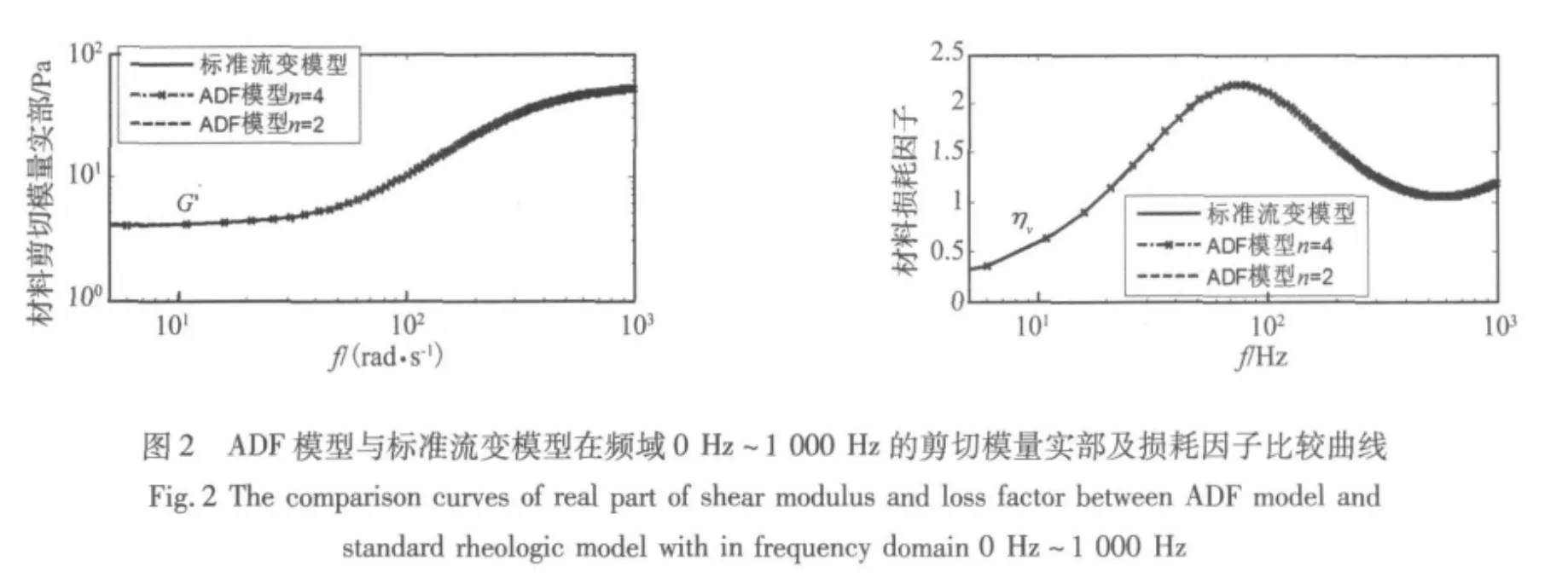
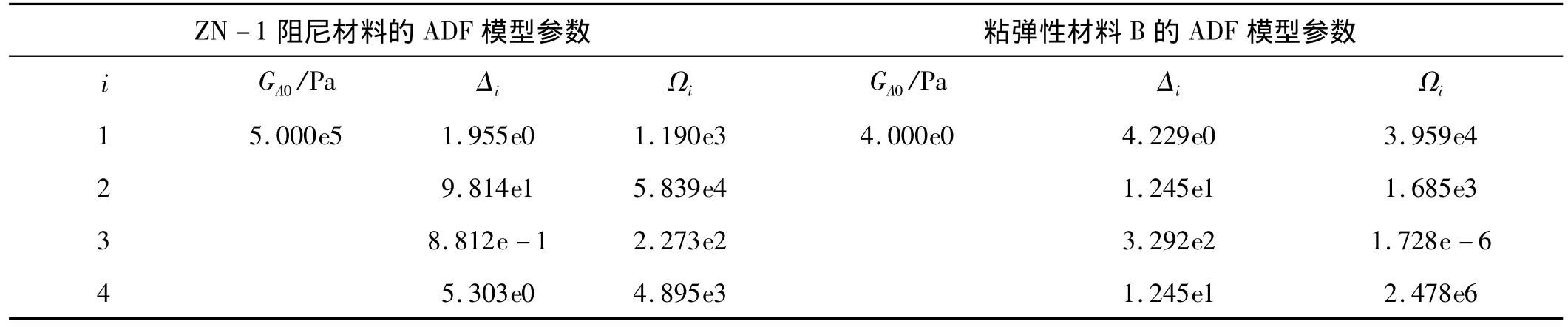
表1 ADF模型n取4时各参数优化结果Tab.1 Parameters optimization results of ADF model at n=4

采用文献［14］描述的ZN-1阻尼材料，其力学性能参数模型为经试验数据［15］拟合得到的分数导数模型:

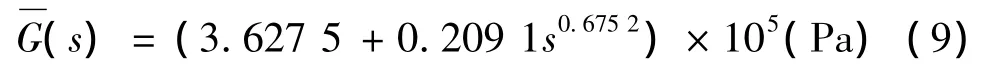
采用文献［16］中描述的粘弹性材料B，其力学性能参数模型为标准流变学模型:

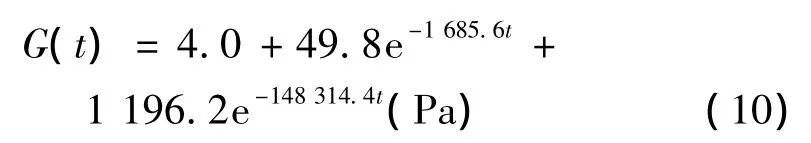
从ADF模型优化结果与两种形式的松弛函数及试验结果的比较图可以看出，本文的ADF模型参数的优化效果明显，模型优化结果与松弛函数模型曲线很靠近，摄动项为4时的曲线要好于摄动项为2时的结果。对于ZN-1阻尼材料，ADF模型9参数优化结果与试验结果拟合较好，可以再现材料的本构特征;对于粘弹性材料B，在整个拟合频段内，ADF模型摄动项为2和4的拟合效果非常接近。图中符号G'，η分别表示材料剪切模量实部及材料损耗因子。

3.2 动力特性计算

为进一步验证ADF模型优化结果的准确性，本文结合ADF模型的数学模型，分别建立了二自由度粘弹性集中参数系统及阻尼夹芯板的动力学模型，进行了模态响应分析及阻尼性能预测，并与文献结果进行比较。对于阻尼夹芯板，还将计算结果与基于迭代算法［17］的ANSYS分析结果进行了比较。采用文献［15］中的集中参数系统，如图3。选用粘弹性材料B作为耗能材料。

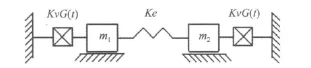
图3 粘弹性集中参数系统Fig.3 Viscoelastic lumped parameter system

系统动力特性矩阵如下，计算结果见表2。

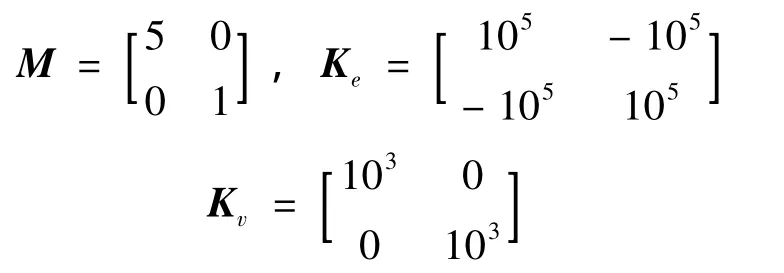
采用文献［16］中的阻尼夹芯板结构，如图3。参数定义为:板件长度La=0.37 m，宽度Lb=0.28 m，基板层为铝合金，基板厚度hb=0.002 5 m，密度 ρb=2 700 kg·m-3，弹性模量Eb=70 GPa，泊松比 νb=0.3;粘弹性层为ZN-1阻尼材料，厚度hv=0.001 m，密度ρv=2 500 kg·m-3，泊松比 νv=0.3，材料力学性能模型见式(8)，其ADF模型参数见表1;约束层为钢板，厚度hc=0.001 m，密度 ρc=5 400 kg·m-3，弹性模量Ec=140 GPa，泊松比 νb=0.3。计算结果见表3～表4。

图4 阻尼夹芯板结构Fig.4 Damped sandwich structures

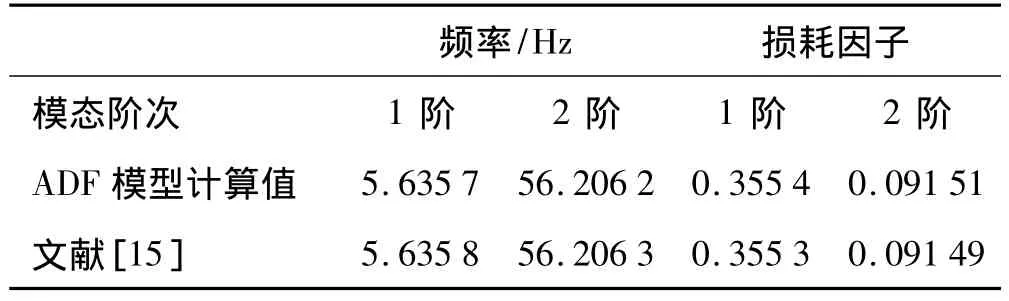
表2 集中参数系统频率及损耗因子Tab.2 Natural frequency and loss factor of viscoelastic lumped parameter system

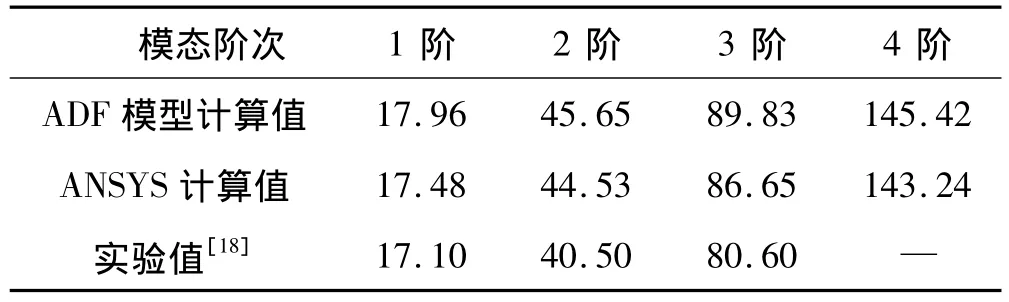
表3 阻尼夹芯板固有频率(Hz)Tab.3 Natural frequency of damped sandwich structures(Hz)

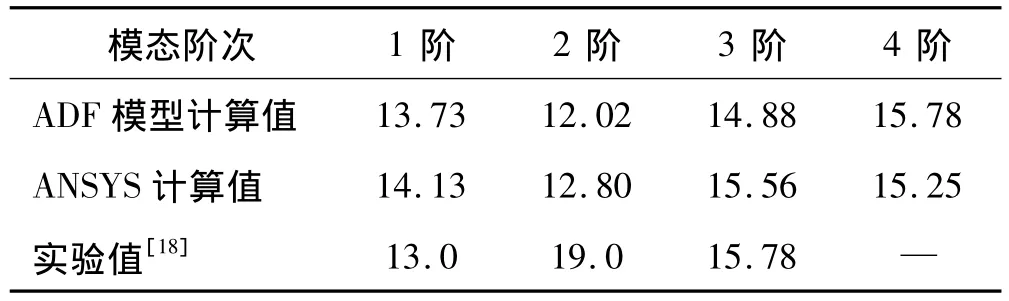
表4 阻尼夹芯板阻尼比(ξ%)Tab.4 Damping ratio of damped sandwich structures(ξ%)

通过算例计算表明，采用本文ADF模型优化参数的计算结果与理论和实验值都很靠近，计算精度相对较高。对于阻尼夹芯板结构，由于文献［16］中约束板根部粘贴有占约束板面积2.3%的压电片，本文忽略，所以本文计算值与实验值略有误差，但与ANSYS计算值的误差在5%以内，结果可信度较高。

4 结论

本文针对阻尼材料ADF模型多参数、多目标、非线性，具有约束条件的优化问题给出了一种新的组合算法寻优求解方法，通过与标准流变模型、分数导数模型两种形式的松弛函数模型及试验结果的拟合比较，表明本文的优化方法可以得到较好的全局优化解，且优化效果明显;将优化结果引入到悬臂夹芯板结构的模态分析及阻尼计算表明，本文优化算法得到的优化结果的准确度高，能准确描述粘弹性材料的本构关系。本文的研究方法可为阻尼类材料各类模型的参数优化问题提供参考，同时对含粘弹性材料的复合结构动力学特性的深入研究提供了有力保障。

［1］戴德沛.阻尼技术的工程应用［M］.北京:清华大学出版社，1991.

［2］Liao W H，Wang K W.On the analysis of viscoelastic materials for active constrained layer damping treatments［J］.J.Sound and Vibr.，1997，207(3):319-334.

［3］Hau L C， Fung E H K.Effect of ACLD treatment configuration on damping performance of a flexible beam［J］.J.Sound Vib.，2004(269):549-567.

［4］张希农，陈 灵，李智明，等.可控约束阻尼层板的杂交控制［J］.应用力学学报，1999，16(3):16-21.

［5］Park S W.Rheological modeling of viscoelastic passive dampers［J］.SmartStructures and Materials，2001:343-354.

［6］Lesieutre G A，Bianchini E.Time domain modeling of linear viscoelasticity using anelastic displacement fields［J］.J.Vib.Acoust.，1995，117(4):424-430.

［7］Lesieutre G A，Lee U.A finite element for beams having segmented active constrained layers with frequency-dependent viscoelastics［J］.Smart Mater. Struct.，1996，5(5)，615-627.

［8］Trindade M A.Reduced-order finite element models of viscoelastically damped beams through internalvariables projection［J］.J.Vib.Acoust.，2006，128(4):501-508.

［9］孙靖民.机械优化设计［M］.北京:机械工业出版社，1999.

［10］王 琼，吕 微，任伟建.免疫遗传算法及在优化问题中的应用综述［J］.计算机应用研究，2009，26(12):4428-4431.

［11］李 丽，牛 奔.粒子群优化算法［M］.北京:冶金工业出版社，2009.

［12］ Kennedy J，Eberhart R C.Particle swarm optimization［C］.IEEE International Conference on Neural Networks，Piscataway:IEEE Service Center，1995:1942-1948.

［13］袁亚湘，孙文瑜.最优化理论与方法［M］.北京:北京科学技术出版社，2001.

［14］陈 前，朱德懋，周蒂莲.粘弹性阻尼结构的动特性分析［J］.航空学报，1986，7(1):36-45.

［15］陈 前.粘弹性复合结构的动力分析［D］.南京:南京航空学院，1987.

［16］任建亭，邱 阳.粘弹性复合结构特征值问题的迭代算法［J］.计算力学学报，1997，14(3):353-359.

［17］孙社营.粘弹阻尼结构动态性能的有限元分析［J］.材料开发与应用，1999，14(6):31-36.

［18］谢石林，张希农，张景绘.可控约束阻尼层结构H∞控制［J］.振动工程学报.2000，13(3):368-375.